当前位置：文档之家 › 放大电路频率特性

放大电路频率特性

  • 格式：doc
  • 大小：1.34 MB
  • 文档页数：17

下载文档原格式

  / 17

合集下载

放大电路的频率特性

放大电路的频率特性

返回＞＞第三章 放大电路的频率特性通常，放大电路的输入信号不是单一频率的正弦信号，而是各种不同频率分量组成的复合信号。

由于三极管本身具有电容效应，以及放大电路中存在电抗元件(如耦合电容和旁路电容)，因此，对于不同频率分量，电抗元件的电抗和相位移均不同，所以，放大电路的电压放大倍数A u 和相角φ成为频率的函数。

我们把这种函数关系称为放大电路的频率特性。

§1频率特性的一般概念一、频率特性的概念以共e 极基本放大电路为例，定性地分析一下当输入信号频率发生变化时，放大倍数将怎样变化。

在中频段，由于电容可以不考虑，中频A um 电压放大倍数基本上不随频率而变化。

ο180=ϕ，即无附加相移。

对共发射极放大电路来说，输出电压和输入电压反相。

在低频段，由耦合电容的容抗变大，电压放大倍数A u 变小，同时也将在输出电压和输入电压间产生相移。

我们定义：当放大倍数下降到中频率放大倍数的0.707倍时，即2umul A A =时的频率称为下限频率f l对于高频段。

由于三极管极间电容或分布电容的容抗在低频时较大，当频率上升时，容抗减小，使加至放大电路的输入信号减小，输入电压减小，从而使放大倍数下降。

同时也会在输出电压与输入电压间产生附加相移。

同样我们定义：当电压放大倍数下降到中频区放大倍数的0.707倍时，即2umuh A A =时的频率为上限频率f h 。

共e 极的电压放大倍数是一个复数，ϕ<=•u u A A其中，幅值A u 和相角ϕ都是频率的函数，分别称为放大电路的幅频特性和相频特性。

我们称上限频率与下限频率之差为通频带。

l h bw f f f -=表征放大电路对不同频率的输入信号的响应能力，它是放大电路的重要技术指标之一。

二、线性失真由于通频带不会无穷大，因此对于不同频率的信号，放大倍数的幅值不同，相位也不同。

当输入信号包含有若干多次谐波成分时，经过放大电路后，其输出波形将产生频率失真。

由于它是电抗元件产生的，而电抗元件又是线性元件，故这种失真称为线性失真。

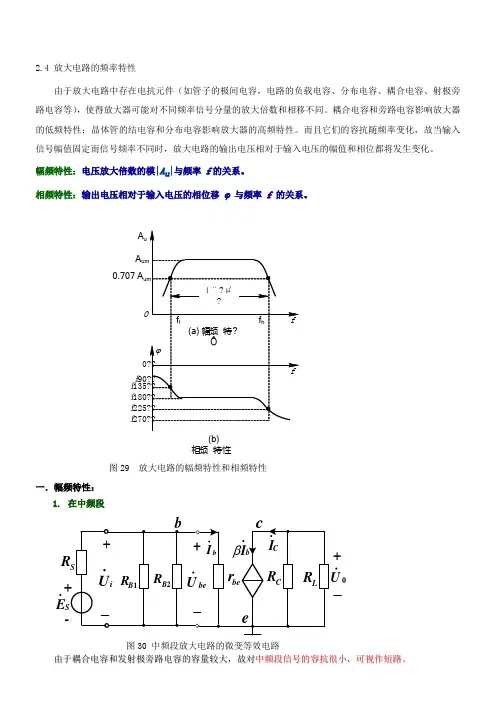
31. 第二章第四节：放大电路的频率特性

31. 第二章第四节：放大电路的频率特性

2.4 放大电路的频率特性由于放大电路中存在电抗元件（如管子的极间电容，电路的负载电容、分布电容、耦合电容、射极旁路电容等），使得放大器可能对不同频率信号分量的放大倍数和相移不同。

耦合电容和旁路电容影响放大器的低频特性；晶体管的结电容和分布电容影响放大器的高频特性。

而且它们的容抗随频率变化，故当输入信号幅值固定而信号频率不同时，放大电路的输出电压相对于输入电压的幅值和相位都将发生变化。

幅频特性：电压放大倍数的模|A u |与频率 f 的关系。

相频特性：输出电压相对于输入电压的相位移 ϕ 与频率 f 的关系。

O0.707 A A A u ￡￡￡￡￡(b)相频特性图29 放大电路的幅频特性和相频特性一．幅频特性：1. 在中频段++SE bI β图30 中频段放大电路的微变等效电路由于耦合电容和发射极旁路电容的容量较大，故对中频段信号的容抗很小，可视作短路。

三极管的极间电容和导线的分布电容很小，可认为它们的等效电容C O 与负载并联。

由于C O 的电容量很小，它对中频段信号的容抗很大，可视作开路。

所以，在中频段可认为电容不影响交流信号的传送，放大电路的放大倍数与信号频率无关而保持定值，输入电压与输出电压反向。

(前面所讨论的放大倍数及输出电压相对于输入电压的相位移均是指中频段的)2. 在低频段：++SE bI β图31 低频段放大电路的微变等效电路由于信号的频率较低，耦合电容和发射极旁路电容的容抗较大，其分压作用不能忽略即不能把它们视为短路，如图31所示。

以至实际送到三极管输入端的电压比输入信号要小，故放大倍数降低，即电压放大倍数的模随频率的降低而减小，输出电压与输入电压的相移也发生变化，并使产生越前的相位移（相对于中频段），不再保持180°的关系。

所以，在低频段放大倍数降低和相位移越前的主要原因是耦合电容和发射极旁路电容的影响。

当放大倍数降到中频段电压放大倍数时所对应得频率L f 为通频带的下限频率。

第三章 放大电路的频率特性

第三章 放大电路的频率特性
Ui Io Ai (dB ) = 20 lg (dB ) Ii
Po • 功率增益 Ap (dB ) = 10 lg P (dB ) i
• 式中， lg是以 为底的对数。 式中， 是以10为底的对数。 是以 为底的对数
• 值得指出的是，如果仅取以10为底的对数，例 值得指出的是，如果仅取以 为底的对数 为底的对数， 无单位”的 必须再乘以20后 如： = lg U o ，是“无单位 的，必须再乘以 后， 无单位 A
• 在横坐标采用 在横坐标采用Lgf时，对数频率特性的主要优点是 时 可以扩宽视野， 可以扩宽视野，在较小的坐标内表示宽广的频率 范围的变化情况， 范围的变化情况，同时将低频段和高频段的特性 都表示得很清楚，而且作图方便， 都表示得很清楚，而且作图方便，尤其对于多级 放大电路更是如此。 放大电路更是如此。因为多级放大电路的放大倍 数是各级放大倍数的乘积，故画对数幅频特性时 数是各级放大倍数的乘积， 只需将各级对数增益相加即可。 ，只需将各级对数增益相加即可。多级放大电路 总的相移等于各级相移之和， 总的相移等于各级相移之和，故对数相频特性的 纵坐标不再取对数。 纵坐标不再取对数。
3.1 频率特性的一般概念
• 3.1.1频率特性的概念 频率特性的概念
– 1.幅频特性和相频特性 幅频特性和相频特性 • 由于电抗性元件的作用，使正弦波信号通过放大 由于电抗性元件的作用， 电路时，不仅信号的幅度得到了放大， 电路时，不仅信号的幅度得到了放大，而且还将 产生一个相位移。此时，电压放大倍数A 产生一个相位移。此时，电压放大倍数 u可表示 为： • Au = Au （f）∠ϕ ( f ) ）
• RC高通电路的对数相频特性如图 高通电路的对数相频特性如图3.1.3（b）所示， 高通电路的对数相频特性如图 （ ）所示， 0 的直线； 在 f ≠ f （ f > 10 f L）时， ϕ 是一条 0 的直线；在 f = f L L 的直线； （ f < 0.1 f L）时，ϕ 是一条900 的直线；在 0.1 f L 之间， 与10 f L 之间，可用一条斜率为 −450 十倍频的直线 来表示。 来表示。由3条直线组成的折线就是它的相频特性 条直线组成的折线就是它的相频特性 曲线，图中的粗线也是加以修正后的实际相频特 曲线， 性曲线。 性曲线。

放大电路的频率特性

放大电路的频率特性

（3）因各级均为共射放大电路，所以在中频段输出电压与输入 电压相位相反。则整个三级放大增益80dB，即放大倍数为 10000。
电压放大倍数
13 104
Au
1
10 jf
1
j
f 2 105
3
*2.7 电路仿真实例
【例2.8】分析共发射极放大电路
解：利用 Multisim 软件仿真如图2.61所示电路。
（3）高频段
耦合电容和旁路电容的容量较大，视为短路；
极间分布电容（含PN结结电容）容抗减小，不能视为开路。
高频源电压放大倍数为：
1
Aush
Uo Us
U
' s
Ub'e
Uo
Us
U
' s
Ub'e
Ri rb'e jRC'
Rs Ri
rbe
1
1 j RC'
gm RL'
Байду номын сангаас
Ausm
1
1 jRC
Ausm 1 1 j
f
fH
在高频段，电压放大倍数随频率升高而减小，相移也发生
变化。其幅频特性基本与低通电路幅频特性相同。
源电压放大倍数的全频率范围表达式为：
jf
Aus
Ausm 1
j
f fL
fL 1
j
f fL
Ausm 1
j
fL f
1
1
j
f fH
单管放大电路的波特图
综上所述，单管放大电路在低频段主要受耦合电容的影 响，表现在放大倍数随频率降低而降低，相移也增大；中频 段可认为其放大倍数和相移都基本为常数（这是放大电路工 作的频段）。在高频段其特性主要受极间电容的影响，表 现在放大倍数随频率升高而下降，相移也随之增大。

放大电路频率特性

放大电路频率特性

第三章放大电路的频率特性§3.1 频率特性的一般概念 一．频率特性的概念对低频段, 由于耦合电容的容抗变大, 高频时1/ωc<<R, 可视为短路, 低频段时1/ωC<<R 不成立。

我们定义: 当放大倍数下降到中频区放大倍数的0.707倍时, 即时的频率称为下限频率fl 。

如图右是考虑频率特性时的等效电路对高频段, 由于三极管极间电容或分布电容的容抗较小, 低频段视为开路, 高频段处1/ωC 较小, 此时考虑极间电容影响的等效电路如图3 - 1(b)所示。

当频率上升时,容抗减小, 使加至放大电路的输入信号减小, 输出电压减小, 从而使放大倍数下降。

同时也会在输出电压与输入电压间产生附加相移。

同样我们定义: 当放大倍数下降到中频区放大倍数的0.707倍, 即Auh=(1 / )Aum 时的频率称为上限频率fh 。

共发射极放大电路的电压放大倍数将是一个复数, 即其中幅度Au 和相角φ都是频率的函数, 分别称为放大电路的幅频特性和相频特性。

可用图3 - 2(a)和(b)表示。

我们称上、 下限频率之差为通频带fbw, 即fbw=fh-fl通频带的宽度, 表征放大电路对不同频率的输入信号的响应能力, 它是放大电路的重要技术指标之一。

二．线性失真线性失真有两种形式：相频失真和幅频失真一个周期信号经傅里叶级数展开后，可以分解为基波、一次谐波、二次谐波等多次谐波。

设输入信号Ui (t )由基波和二次谐波组成，如图（a ）所示, 经过线性电路后， 基波与二次谐波振幅之间的比例没有变化， 但是它们之间的时间对应关系变了，叠加合成后同样引起输出波形不同于输入波形， 这种线性失真称之为相频失真。

线性失真的第一种形式如图（b ）所示。

假设输入波形Ui(t)仅由基波、二次谐波构成， 它们之间的振幅比例为10∶6，如图（b ）上所示。

该输入波形经过线性放大电路后，由于放大电路对不同频率信号的不同放大倍数，使得这些信号之间的比例发生了变化， 变成了10∶3，这二者累加后所得的输出信号Uo(t)如图(b)下所示。

放大电路频率特性总结

放大电路频率特性总结

高频区： f&uarr; &rarr; &#981; 在 180 &#8728; 基础上产生 0 &#8728; ~&minus; 90 &#8728; 相移。 中频区： &#981;= 180 &#8728; ，输出与输入反相(如第二章分析结果)。 3.低频区：当 A u = 1 2 A um 时, f= f L 下限频率 高频区： 当 A u = 1 2 A um 时, f= f H 上限频率 BW= f H &minus; f L 通频带。表明放大电路对不同频率信号的响应能力的 大小。通频带愈宽，放大电路对不同频率信号的响应能力愈强。 4.受通频带限制，当输入信号包含有多个频率信号时 &rarr; 频率失真。它 包含幅频失真和相频失真。 幅频失真：放大电路对输入信号中不同频率的谐波分量的放大倍数不同造 成的失真。 相频失真：放大电路对输入信号中不同频率的谐波分量的相移不同造成的 失真。 频率失真属于线性失真。 5.三极管极间电容的存在会影响到三极管对高频信号的放大能力，三极管 对高频信号的放大能力可用三极管的频率参数描述。
放大电路频率特性总结
1.耦合电容、旁路电容、极间电容存在 &rarr; 阻抗随频率变化 &rarr; 放大倍数是频率的函数频率响应(频率特性)，它包括幅频特性和相频特性。 2.共射放大电路幅频特性显示： 低频区： f&darr; &rarr; A u &darr; 。 原因：耦合电容的存在。 高频区： f&uarr; &rarr; A u &不随 f 变化。 原因：耦合电容和极间电容的影响很小，可忽略。 共射放大电路相频特性显示： 低频区： f&darr; &rarr; &#981; 在 180 &#8728; 基础上产生 0 &#8728; ~ 90 &#8728; 相移。

第三章 放大电路的频率特性

第三章 放大电路的频率特性

第三章放大电路的频率特性本章研究输入信号的频率不同时，对放大电路电压放大倍数的不同影响及线性失真问题。

着重分析电路参数对放大电路通频带的影响。

本章内容：3.1 频率特性的一般概念3.2 三极管的频率特性3.3 共发射极放大电路的频率特性3.4 多级放大电路的频率特性本章要点：1. 放大电路频率特性的概念2. 三极管的频率参数3. 电路参数对放大电路通频带的影响4. 多级放大电路的通频带与级数的关系电子课件三:放大电路的频率特性课时授课教案一授课计划批准人：批准日期：课序：7 授课日期：授课班次：课题：第三章第3.1节频率特性的一般概念目的要求：1. 了解信号频率对电压放大倍数的影响。

2. 了解放大电路产生线性失真的原因。

3. 掌握影响放大电路通频带的因素。

重点：影响放大电路通频带的因素难点：线性失真教学方法手段：结合电子课件讲解教具：电子课件、计算机、投影屏幕复习提问： 1. 电容和电感元件的阻抗与频率的关系？2. 何谓三极管的PN结结电容？课堂讨论：RC滤波电路的特性？布置作业：课时分配：二 授课内容3.1 频率特性的一般概念3.1.1 频率特性的概念下面以共发射极放大电路为例进行分析。

当输入信号的频率不同时，不仅放大电路电压放大倍数的模不一样，而且输入电压与输出电压的相位关系（简称相移）也不一样。

一、 中频段在中频段，即通带内，因为耦合电容和旁路电容的容量较大，其容抗可忽略不计，把他们视为短路；又因为极间分布电容（含ＰＮ结结电容）很小，其容抗很大，可把他们视为开路；感抗视为短路。

可认为电压放大倍数基本与频率无关而保持定值，输入电压与输出电压反相位。

二、低频段当输入信号的频率逐渐降低时，耦合电容和旁路电容的容抗逐渐增大，不能把它们视为短路，如图３-1(a)所示。

电压放大倍数的模随频率的降低而减小，输出电压与输入电压之间的相移也发生变化，不再保持o180的关系。

当放大倍数降到中频段电压放大倍数的21时所对应的频率l f 为通频带的下限频率，如图3-2(a)所示，相移ϕ如图3-2(b)所示。

3.2 放大电路的频率特性

3.2 放大电路的频率特性

U U o3 A A ... o A u1 u2 un U i3 U in
20 lg A 20 lg A 20 lg A 20 lg A u u1 u2 un
= 1 + 2 + · · ·+ n
例如：两级放大电路，假设每级具有相同的频率特性，即 中频区电压放大倍数Aum1、下限频率 f L1、上限频率 f H1 均相同。则总的中频区电压增益为
表3.2.1 电压放大倍数Au与分贝数的关系
Au 10–3 10–2 10–1 0.2 0.707 –3
1
0
2
6.0
3
0.477
9.5
10
102
103 104
lg Au
20lg Au/dB
–3
–60
–2
–40
–1
–20
–0.699
–14
–0.149 0 0.301
1
20
2
40
3
60
4
80
二、波特图
2. 上限频率 f H 的计算 （1）发射结电阻 Rs 26 mV 510 rb' e (1 ) I E (mA) U +
= 1.1 k
s
b
rbb’
30ቤተ መጻሕፍቲ ባይዱ
b’ Cb’e +
+ Ub’c
Cb’c
+ Ui
–
–
rb’e Rb 470 k 1.1 k
e
(Uo’)
c
Ub’e （1-A)Cb’c
三、共基极截止频率 — f 为 下降为 0.707 0 时对应的频率。

放大电路的频率特性

放大电路的频率特性

放大电路的频率特性为了便于讨论，都假定了输入信号vi是单一频率的正弦波，而实际工作中所要放大的信号并不是单一频率的正弦波。

如电视信号中的图像信号，其频率包括了6～6MHz范围内各种频率重量。

由于放大电路中电抗元件的存在，放大电路对不同频率重量的信号放大力量是不相同的，而且不同频率重量的信号通过放大电路后还会产生不同的相移。

因此，衡量放大电路放大力量的放大倍数也就成为频率的函数。

放大电路的电压放大倍数与频率的关系称为幅频特性,输出信号与输入信号的相位差与频率之间的关系称为相频特性。

两者统称频率特性。

由于电抗元件的电抗是频率的函数，随着频率的变化而变化。

如电路中的耦合电容和射极旁路电容，在频率较低时，其容抗较大，它们对沟通信号不能视为短路，这就必需考虑其容抗对电路的影响。

在分析放大电路的频率特性时，通常采纳频率分段法进行分析，即将放大电路的工作频率范围划分为低频、中频和高频三个频段，分别求出各频段中的频率特性，然后综合求得完整的频率特性。

放大电路的频率特性中有三项性能指标，它们是：图 1 放大电路的频率特性（a）幅频特性（b）相频特性1．下限频率在低频段，放大电路的电压放大倍数降到中频段电压放大倍数Avo的0.707Avo时的频率值叫做下限频率fL，如图1（a）所示。

引起低频段电压放大倍数下降的缘由主要是输入耦合电容、输出耦合电容和射极旁路电容，对低频信号形成较大的衰减，从而使电压放大倍数下降。

2．上限频率在高频段，放大电路的电压放大倍数降到中频段电压放大倍数Avo的0.707Avo时的频率值叫做上限频率fH，如图1（a）所示。

引起高频段电压放大倍数下降的缘由主要是三极管的极间电容和放大电路的输入电路和输出电路的分布电容，将高频信号旁路，从而使电压放大倍数下降。

3．通频带在频率特性的中频段，放大电路的各种电容对沟通信号的影响均可以忽视，因此电压放大倍数Avo基本不变。

这个频率带宽B ＝fH －fL，称B为通频带。

电子技术基础第五章 放大电路的频率特性

电子技术基础第五章 放大电路的频率特性

对数幅频特性和相频特性表达式为 20lg| |=20lg| |–20lg
四、波特图
图5.4.5
5.4.2 单管共源放大电路的频率响应
图5.4.7
5.4.3 放大电路频率响应的改善和增益带宽积 为改善低频特性，需加大耦合电容及其回路 路电阻以降低下限频率，直接耦合方式，下限 频率为0。 为改善高频特性，需减小 或 及其回路 电阻，以增大上限频率。
二、超前补偿
图5.6.6
图5.6.7
5.7 频率响应与阶跃响应
5.7.1 阶跃响应的指标 1、上升时间tr： 0.1Um~0.9Um的时间 2、倾斜率δ
3、超调量：上升值 超过终了值的部 分，一般用百分 比来表示。 图5.7.2
5.7.2 频率响应与阶跃响应的关系
图5.7.3 所在回路是低通回路,在阶跃信号作用时, 上的电压 将按指数规律上升,其起始值为 0,终了值为 ,回路时间常数为 ,因而
5.2 晶体管的高频等效模型
5.2.1 晶体管的混合π模型 一、完整的混合π模型
图 5.2.1
二、简化的混合π模型
图 5.2.2
等效变换: 在图(a)电路中,从b’看进去Cμ中流过的电流为
为保证变换的等效性，要求流过 的电流仍 为 ，而它的端电压为 ，因此 的电抗为
在近似计算时， 取中频时的值，所以 | | = 说明 是 的 （1+| |）分之一，因此 | |） 间总电容为 | 用同样的方法可以得出 |）
要减小 ，则要减小 ，这将使电压放大 倍数减小。可见提高 和增大电压放大倍数是 矛盾的。
单管共射放大电路的增益带宽积为 | || |
设 则 |
，则 ；设 。 则 |
；设
，则
，且

放大电路的频率特性

放大电路的频率特性

幅频特性
幅频特性是描绘放大倍数的幅度随频率变化 而变化的规律。即 Au F( f )
相频特性
相频特性是描绘输出信号与输入 信号之间相位差随频率变化而变化 的规律。即 ∠A ∠U o ∠U i ( f )
Au Aum 0.707 Aum
典型的单管共射放大电路的幅频特性和相频特性
fZ 20dB/ 十倍频
f

90o
45o
f
0
0.1 fZ f Z 10 fZ
例1、
Au

10 6 jf 10 4
解、
20lg Au / dB
40
A u

10 6
10 4 (1
j
f 10
4
)
102
1
j
f 104
0
20

0
45o 90o
103 104 105
f / Hz
f / Hz
f fH
20lg Au
0dB
0dB 3dB 20dB 20lg( f fH )
0o 5.710 450 84.290
900
幅频响应：

│Au│
1 1 ( f fH)2
当 f fH 时，
20 lg | Au （| dB）
0.1fH fH 10fH 100fH
线称为波特图，是分析放大电路频率响应的重要手段。
（2）RC 高通电路
电压传输系数的幅频特性和相频特性
Au

U o U i
令
fL

1
2RC
f
j
则
Au
1 1 j
fL

放大电路的频率特性

放大电路的频率特性

U o U o1 U o 2 Au U i U i U o1 U o1 U o 2 Ui Ui2 Au1 Au 2 U oN U iN
U oN U o ( N 1)
AuN Aui
i 1
N
注意：计算每一级的电压放大倍数时，应 将其后一级电路的输入电阻当作它的负载
Ao 2 AF 2
AF
Ao 1 Ao FAF Bo BF来自f多级放大电路
电压放大
前置级 输 入 前置级 第二级 放大电路 第 n级 放大电路 末级 前置级
第一级 放大电路
……
第n-1级 放大电路
输 出 两个单级放大电 路间的联接方式。 实现信号传递
末前级
功率放大
耦合方式：阻容耦合；直接耦合；变压器耦合；光电耦合。
理想情况：ui1 = ui2 VC1 = VC2 uo= 0 共模电压放大倍数： AC
uo uc
(理想时为零)
(2) 差模输入： ui1 = -ui2 = ud
UCC RB2
RB1 ui1
RC
T1
uo T2
RC
RB2
RB1
ui2
设 vC1 =VC1 +VC1 ， vC2 =VC2 +VC2 因 ui1 = -ui2， VC1 = -VC2 uo= vC1 - vC2= VC1- VC2 = 2VC1
阻容耦合电压放大电路
射极输出器 分压式偏置 放大电路
+UCC (+24V)
负载
R1
信号源
R2
RC2 10k T2
1M
C2
82k
C1
RS 20k
T1
  1. 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
  2. 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
  3. 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

第三章放大电路的频率特性§3.1 频率特性的一般概念 一．频率特性的概念对低频段, 由于耦合电容的容抗变大, 高频时1/ωc<<R, 可视为短路, 低频段时1/ωC<<R 不成立。

我们定义: 当放大倍数下降到中频区放大倍数的0.707倍时, 即时的频率称为下限频率fl 。

如图右是考虑频率特性时的等效电路对高频段, 由于三极管极间电容或分布电容的容抗较小, 低频段视为开路, 高频段处1/ωC 较小, 此时考虑极间电容影响的等效电路如图3 - 1(b)所示。

当频率上升时,容抗减小, 使加至放大电路的输入信号减小, 输出电压减小, 从而使放大倍数下降。

同时也会在输出电压与输入电压间产生附加相移。

同样我们定义: 当放大倍数下降到中频区放大倍数的0.707倍, 即 Auh=(1 / )Aum 时的频率称为上限频率fh 。

共发射极放大电路的电压放大倍数将是一个复数, 即其中幅度Au 和相角φ都是频率的函数, 分别称为放大电路的幅频特性和相频特性。

可用图3 - 2(a)和(b)表示。

我们称上、 下限频率之差为通频带fbw, 即fbw=fh-fl通频带的宽度, 表征放大电路对不同频率的输入信号的响应能力, 它是放大电路的重要技术指标之一。

二．线性失真线性失真有两种形式：相频失真和幅频失真一个周期信号经傅里叶级数展开后，可以分解为基波、一次谐波、二次谐波等多次谐波。

设输入信号Ui (t )由基波和二次谐波组成，如图（a ）所示, 经过线性电路后， 基波与二次谐波振幅之间的比例没有变化， 但是它们之间的时间对应关系变了，叠加合成后同样引起输出波形不同于输入波形， 这种线性失真称之为相频失真。

线性失真的第一种形式如图（b ）所示。

假设输入波形Ui(t)仅由基波、二次谐波构成， 它们之间的振幅比例为10∶6，如图（b ）上所示。

该输入波形经过线性放大电路后，由于放大电路对不同频率信号的不同放大倍数，使得这些信号之间的比例发生了变化， 变成了10∶3，这二者累加后所得的输出信号Uo(t)如图(b)下所示。

对比Ui(t), 可见两者波形发生了很大的变化，这就是线性失真的第一种形式，即幅频失真。

U iR U oC(a ) 低频段耦合电容的影响U iU o C(b ) 高频段极间电容的影响＋－－＋－＋－)2/1(1um u A A =2通频带0.707 A umA A u f lf hff0°－90°－135°－180°－225°－270°(b ) 相频特性ϕϕ∠=u u A A§3.2 三极管的频率参数（1） （2） （3）β的幅频特性一． 共发射极电流放大系数β的截止频率f β将 值下降到β0的0.707倍时的频率f β定义为β的截止频率。

按公式(3 - 4)也可计算出, 当f=f β时,二． 特征频率f定义 值降为1时的频率fT 为三极管的特征频率。

将f=fT 和 代入(2)式, 则得由于通常fT ／f β>>1, 所以上式可简化为 fT ≈β0f β 上式表示了fT 和f β的关系。

基波二次谐波tOu itu oO(a ) 相频失真tOu i基波u oOt基波二次谐波(b ) 幅频失真基波二次谐波二次谐波ββββββββf f Q f f f fjarctan)(11200-=+=+=••O0.707β0β0βf βf T·•β00707.0)2/1(βββ≈=••β1=•β211⎪⎭⎫⎝⎛+=ββf f T三． 共基极电流放大系数α的截止频率f α由上述和的关系得（4） （5）下降为中频α0的0.707倍时的频率f α为α的截止频率。

定义当f α、f β、 fT 之间有何关系? 将式(1)代入式(4)得四． 三极管混合参数π型等效电路 1.完整的混合π型模型（1） 混合π型参数和h 参数之间的关系•••+=ββα1.•α•βαααf f jo+=•1.•αββββββββαf fjf jf f jf )1(11/11/10000+++=+++=•Ta a f f f f f =≈+=ββββ00)1(bc(b ) 混合 π 型 等效电路ee(a ) 三极管的电容效应bbI I (a ) 不考虑C π和C μ的简化混合π型等效电路bI I (b ) 简化的h 参数等效电路2. 简化的混合π型模型（2）C μ的等效过程令此式表明, 从b ′、e 两端看进去, 跨接在b ′、c 之间的电容C μ的作用, 和一个并联在b ′、e 两端, 其电容值为 的电容等效。

这就是密勒定理。

如图（2）中（c ）所示。

26262626)1(26)1('''''''''CQCQeb m b e b b m e b m eb be bb CQEQ e b EQbb be e b bb I I r g I r I g U g r r r I I r I r r r r =====-=≈+=++==+βββββββππC g f mT 2≈(a )r .C μc(b )U .C b′eU c e.e(c )μμωωC j U U U C j U U I eb ce e b ce e b 1)1(1''''•••••--=-=则,'K U U eb ce -=••μμωωC K j U C j K U I e b e b )1(11)1('''+=+=••μπC K C )1('+=μμμωωωC KK j U C j K U C j U U I ce e c eb ce )1(11)11(1'''+=+=-=••••§3.3 共e 极放大电路的频率特性（1） 共e 极放大电路及其混合π型等效电路具体分析时, 通常分成三个频段考虑:(1) 中频段: 全部电容均不考虑, 耦合电容视为短路, 极间电容视为开路。

(2) 低频段: 耦合电容的容抗不能忽略, 而极间电容视为开路。

(3) 高频段: 耦合电容视为短路, 而极间电容的容抗不能忽略。

这样求得三个频段的频率响应, 然后再进行综合。

这样做的优点是, 可使分析过程简单明了, 且有助于从物理概念上来理解各个参数对频率特性的影响。

下面分别讨论中频，低频，高频时的频率特性。

一． 中频放大倍数Ausm 由图（2），可得（2）中频段等效电路由上述关系代入Uo 的表达式中，得＋－sR b r b eR c＋－＋－U ss C 1R L＋U C CR cR b＋C 2(b )bcU o.U i.U s.U i.C 1bb′C πU o .C K ＋1Kg m U b e′.U b e ′＋e′b ′′＋－R sR b＋－bcU ir U og m U b e ′′U r b e ′U b e ′R ceb eb bb e b e b bb b i sis ii ii e b s ii ii eb bb e b e bc e b m O r r r p r r R r U r R r U pU U r R r U pU U r r r U R U g U ''''''''''');//(+=+=+==+==+=-=3-31 二．低频放大倍数A usl 及波特 由图（3），可得 3．32 （3）低频段等效电路式中p 、r i 同中频段的定义。

将 、 代入式3-32, 得将公式(3 - 31)代入, 并令3-333-34sc m is is c m e b bb e b i s i O U R pg r R r U R g r r r r R r U ••+=+⋅+-='''cm is i s O usm R pg r R r U U A +-==•••••••++==+=-=s i s i i i i e b bb e b e b ce b m O U C j r R r U U p U r r r U R U g U 11'''''ω••++-=sc m i s io U R pg C j r R r U 11ωe b U '•iU •si s c m is i o U C r R j R pg r R r U ••++⋅+-=1)(111ω11)(111C r R j R pg r R r U U A i s c m i s i s O us ++⋅+-==•••ωff j A j A A C r R f C r R usmusm us i s i s 1111111111111)(2121)(-=+=+==+=•ωτππττ,121usm us A A =•当f=fl 时, ， fl 为下限频率。

由(3 - 33)式可看出, 下限频率fl 主要由电容C1所在回路的时间常数τl 决定。

将式(3 - 34)分别用模和相角来表示:3-353-36根据公式(3 - 35)画对数幅频特性, 将其取对数, 得3-37先看式(3 - 37)中的第二项, 当f>>f l 时故它将以横坐标作为渐近线；当f<<f l 时其渐近线也是一条直线，该直线通过横轴上f=f1这一点，斜率为20db/10倍频程。

（4）低频段对数频率特性低频段的相频特性, 根据式(3 - 36)可知,ff f f A A usm us 1211arctan1801+︒-=⎪⎭⎫ ⎝⎛+=•ϕ211120120120⎪⎪⎭⎫ ⎝⎛+-==•f f g A g A Ig G usm us u 0120121≈⎪⎪⎭⎫⎝⎛+-f f g 0120121≈⎪⎪⎭⎫ ⎝⎛+-f f g 11212012011201f fg f f g f f g =-≈⎪⎪⎭⎫ ⎝⎛+-－－(a ) 幅频特性G u / dBϕ－(b ) 相频特性当f>>fl 时, 趋于0, 则φ≈-180°; 当f<<fl 时, 趋于90°,φ ≈-90°;当f=fl 时, , φ =-135°。

这样可以分三段折线来近似表示低频段的相频特性曲线, 如图（4）(b)所示。

f ≥10fl 时, φ =-180°f ≤0.1fl 时,φ =-90°0.1fl ＜f ＜10fl 时, 斜率为-45°/10倍频程的直线。