RC电路的频率特性剖析

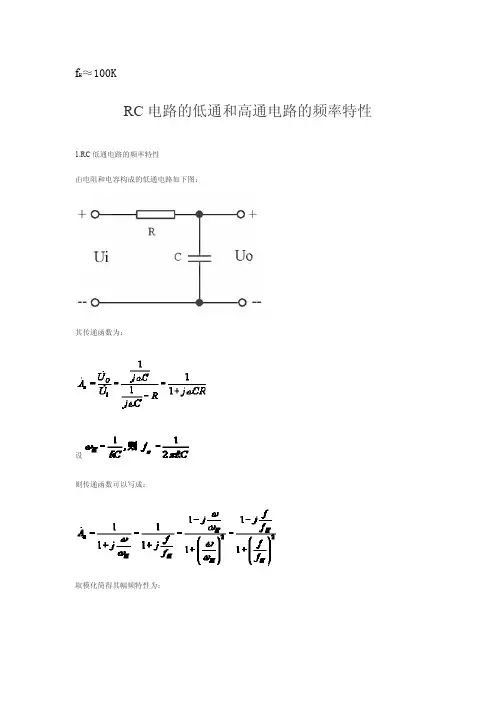
f H≈100KRC电路的低通和高通电路的频率特性1.RC低通电路的频率特性由电阻和电容构成的低通电路如下图：其传递函数为：设则传递函数可以写成：取模化简得其幅频特性为：相频特性为：从其幅频特性曲线如下图，可以看出，当频率f升高时，|Au|逐渐下降，当f=f H时，|Au|=1/√2=0.707，所以我们称f H为低通滤波的上限截止频率，其通频带为0~f H。

因电路只有一个储能元件，所也也称一阶低通滤波电路。

工程上为了作图简便，常用波特图表示，如下图，其中细实线为实际曲线，粗实线为实际曲线的渐近线。

当f≤0.1f H时，近似认为|Au|≈1，即|Au|=(20lg|Au|)dB=0dB当f≥10f H时，近似认为|Au|=1/（f/f H）,也即|Au|≈20lg（f H/f）根据上图可以看出，当f≤0.1f H时，幅频物性的波特图为一条水平线，当f≥10f H时是一条-20dB/十倍频的斜线，两线在f=f H处相交，因此f H也称为转折频率。

在粗略计算时，可以用渐近线代替实际曲线，最大误差发生在f H处，误差为|20lg0.707|dB=20×0.15dB=3dB。

当f≤0.1f H时，相频特性曲线，可以看成φ=0的近似线，当f≥10f H时，近似认为φ=-90，当f=f H时，φ=-45。

在0.1f H<f<10f H区域内，可用一条斜率为-45/十倍频的斜线代替。

其中f=0.1f H和f=10f H误差最大，为5.7度。

2.RC高通电路的频率特性电如如下图：其传递函数为：设由传递函数可写成：取模得其幅频特性：相频特性为：根据其特性可以绘出RC高通电路的波特图其下限截止频率为f L ，通频带为f L ~∞。

为一阶高通滤波。

综合上述的低通和高通滤波电路，它们对信号只有衰减作用，没有放大作用，因些称为无源滤波电路。

上述两种电路常用在有源滤波电路中，在电子分频的音响功放中也比较常见，比如我们可用上述电路，把音响的输入信号二分频后分别进行放大，来代替昂贵的分频器。

RC电路的频率特性RC电路的频率特性:=1/（2πfC），在RC串联的正弦交流电路中，由于电容元件的容抗XC它与电源的频率有关，所以当输入端外加电压保持幅值不变而频率变化时，其容抗将随频率的变化而变化，从而引起整个电路的阻抗发生变化，电路中的电流及在电阻和电容元件上所引起的电压也会随频率而改变。

我们将RC电路中的电流及各部分电压与频率的关系称为RC电路的频率特性。

截止频率是用来说明电路频率特性指标的一个特殊频率。

当保持电路输入信号的幅度不变，改变频率使输出信号降至最大值的0.707倍时，此频率即为截止频率。

截止频率公式1f0=RCπ2高通滤波器07.0T f ()（a ）实验电路（b ）幅频特性曲线图1高通滤波器低通滤波器07.0T f ()（a ）实验电路（b ）幅频特性曲线图2低通滤波器RC串并联选频电路10（a ）实验电路（b ）幅频特性曲线图3 选频电路实验目的（1）测量RC电路的频率特性，并画出其频率特性曲线。

（2）掌握测量截止频率的方法。

（3）进一步熟悉相关实验仪器的用途及使用方法。

图1 高通滤波器提示：在测量过程中应注意，在频率改变的同时用电压测试仪监测输入电压幅度，使之保持恒定。

表1 高通滤波器实验数据计算值：f 0= 测量值：f 0=图2低通滤波器表2 低通滤波器实验数据计算值：f 0= 测量值：f 0=图3选频电路1表3选频电路实验数据= 测量值：f0=计算值：f3 注意事项实验中，请同学们注意：（1）信号发生器输出端不可短路（2）测量交流高频信号电压有效值，须使用测试仪SCOPE 功能，不允许使用万用表（3）在测试仪的监测下，始终保持信号发生器输出电压有效值不变。

实验七 RC 电路频率特性一、实验目的1、了解低通和高通滤波器的频率特性，熟悉文氏电桥的结构特点及选频特性；2、掌握网络频率特性测试的一般方法；二、实验仪器信号发生器、交流毫伏表、数字频率计、双踪示波器三、实验原理1、文氏电路如图1所示，电路输出电压和输入电压的幅值分别为Uo 、Ui ，相位分别为φo 、φi ，输出电压和输入电压的比为网络函数，记为H （j ω），网络函数的幅值为∣H （j ω）∣=Uo/Ui ，相位为φ＝φo －φi ，∣H （j ω）∣和φ分别为电路的幅频特性和相频特性。

文氏电路的网络函数表达式为：文氏电路的幅频特性和相频特性见图2和3，在频率较低的情况下，即1/C R ω>>时，电路可近似等效为图4所示的低频等效电路。

频率越低，输出电压的幅度越小，其相位愈超前于输入电压。

当频率接近于0时，输出电压趋近于0，相位接近90度。

而当频率较高时，即当1/C R ω<<时，电路电路可近似等效为图5所示的高频等效电路。

频率越高，输出电压的也幅度越小，其相位愈滞后于输入电压。

当频率接近于无穷大时，输出电压趋近于0，相位接近－90度。

由此可见，当频率为某一中间值o f 时，输出电压不为0，输出电压和输入电压同相。

∣H （j ω）∣ φ图1 RC 文氏电路 图2 文氏电路幅频特性 图3 文氏电路相频特性31arctan)1(31)1(31)(22RC RC RCRC RCRC j UU j H io ωωωωωωω-∠-+=-+==u o+--1/390图4 低频等效电路 图5 高频等效电路2、实验测量框图如图6所示，信号源与RC 网络构成回路，将信号源输出信号和RC 网络端输出信号接入示波器，用频率计测量信号源输出信号的频率。

图6 实验框图 图73、RC 带通网络中心频率0f 的测定当带通网络的频率0f f 时，输入电压和输出电压的相位差为0，如果在示波器的垂直和水平偏转板上分别加上频率、振幅和相位相同的正弦电压，则在示波器的荧光屏上将得到一条与X 轴成45度的直线。

f H≈100KRC电路的低通和高通电路的频率特性1.RC低通电路的频率特性由电阻和电容构成的低通电路如下图：其传递函数为：设则传递函数可以写成：取模化简得其幅频特性为：相频特性为：从其幅频特性曲线如下图，可以看出，当频率f升高时，|Au|逐渐下降，当f=f H时，|Au|=1/√2=0.707，所以我们称f H为低通滤波的上限截止频率，其通频带为0~f H。

因电路只有一个储能元件，所也也称一阶低通滤波电路。

工程上为了作图简便，常用波特图表示，如下图，其中细实线为实际曲线，粗实线为实际曲线的渐近线。

当f≤0.1f H时，近似认为|Au|≈1，即|Au|=(20lg|Au|)dB=0dB当f≥10f H时，近似认为|Au|=1/（f/f H）,也即|Au|≈20lg（f H/f）根据上图可以看出，当f≤0.1f H时，幅频物性的波特图为一条水平线，当f≥10f H时是一条-20dB/十倍频的斜线，两线在f=f H处相交，因此f H也称为转折频率。

在粗略计算时，可以用渐近线代替实际曲线，最大误差发生在f H处，误差为|20lg0.707|dB=20×0.15dB=3dB。

当f≤0.1f H时，相频特性曲线，可以看成φ=0的近似线，当f≥10f H时，近似认为φ=-90，当f=f H时，φ=-45。

在0.1f H<f<10f H区域内，可用一条斜率为-45/十倍频的斜线代替。

其中f=0.1f H和f=10f H误差最大，为5.7度。

2.RC高通电路的频率特性电如如下图：其传递函数为：设由传递函数可写成：取模得其幅频特性：相频特性为：根据其特性可以绘出RC高通电路的波特图其下限截止频率为f L ，通频带为f L ~∞。

为一阶高通滤波。

综合上述的低通和高通滤波电路，它们对信号只有衰减作用，没有放大作用，因些称为无源滤波电路。

上述两种电路常用在有源滤波电路中，在电子分频的音响功放中也比较常见，比如我们可用上述电路，把音响的输入信号二分频后分别进行放大，来代替昂贵的分频器。

指导教师： 王吉英 2009 年 11 月 13 日 计算机科学与技术 学院 姓名： 钟超 学号： PB06013012 姓名： 李杰 学号： PB05210127实验目的1. 熟悉正弦稳态分析中的相量的基本概念。

2. 正确使用双踪示波器测量正弦信号的峰—峰值Up-p ，频率f(T)和相位差φ,观察李沙育图形; 学会使用晶体管毫伏表测量正弦信号有效值。

3. 用RC 、RL 设计输出滞后(超前)输入的简单电路，并作实际测量。

实验设备1. DF1641D 型或EE1641D 型函数发生器1台2. 双踪示波器 1台3. 晶体管毫幅表DF2173B 1台4. 可变电容箱1个5. 可变电阻箱1个6.可变电感箱1个实验原理1． 正弦交流电作用于任一线性定常电路，产生的响应仍是同频率的正弦量，因此，正弦量可以用相量来表示。

设一正弦电流：[]Ii j t j e tj j ei Ie I e I R Ie R t ICOS t i ϕωωϕϕω=↔⎥⎦⎤⎢⎣⎡=+=∙∙+22)(2)(2． 用相量表示了正弦量，正弦交流稳态响应的计算可方便地运用相量进行复数运算，在直流电路中的基本定律、定理和计算方法完全适用于相量计算。

3． 输出电压滞后输入电压的RC 电路，如图1所示。

图1(RC 滞后电路) 图2(RC 超前电路)输出电压1110+=+=∙∙CR j U U Cj R C j U i i ωωωUNIVERSITY OF SCIENCE AND TECHNOLOGY OF CHINASchool of Computer Science & Technology, Hefei, Anhui, People's Republic of China, Zip Code: 230027RC 电路的频率特性实验报告网络函数为：()())()(11)(120ωϕωωωω∠=-∠+==-∙∙j H RC tg RC U U j H i式中，2)(11)(RC U U j H io ωω+=∆∙∙，称为幅频特性，显然是低通。

RC网络的频率特性及元件参数对频率特性的影响一、RC网络电路1.RC串并联网络电路(见图1)电路分析。

如图1所示,其中为网络的输入电压,为输出电压。

串联和并联支路的电阻、电容分别为R1,R2,C1,C2,则Z1=R1+, Z2=。

则RC串并联网络中,网络传输(反馈)系数的频率特性为==,则=(1)2.RC并串联网络(见图2)电路分析。

如图2所示,U1是输入电压,U2是输出电压。

若并联和串联支路中的电阻R1,R2, 对应的电容为C1,U2,Z1=,Z2=,因此网络传输系数的频率特性为:=== ,化简得: =+-(2)二、RC网络的元件参数变化的影响1.RC串并联网络中的参数变化的影响由公式(1)=,当R1=2R2,C1=C2时,上式可化简为:=(3)令ω0=,则幅频特性:= (4)相频特性:ΦF=-arctan(5)当R1=R2,C1=2C2时,公式(1)可化简为:=(6)令ω0=其幅频特性为公式(4),而相频特性为(5)。

当ω=ω0时,RC串并联网络的传输系数最大,最大值为=,此时相位为ΦF =0。

而当电阻R1=R2=R,电容为C1=C2=C时,其幅频为=,相频为ΦF =-arctan,当ω=ω0时,RC串并联网络的传输系数最大,最大值为=。

由此可见,只有在电阻、电容分别相等的情况下,网络的传输系数才最大。

网络中的电阻、电容的变化对频率特性有很大影响。

2.RC并串联网络中的参数变化的影响由公式(2),=+-当取R1=2R2,C1=C2时,代入上式可得网络传输系数的频率特性为:=+-(7)令ω0=,则上式可化为:=(8)当ω=ω0时,RC并串联网络的传输系数最小,最小值为=,此时相位ΦF =0为。

而当ω>ω0(或ω。

RC振荡电路的幅频特性及其调节方法RC振荡电路是一种常见的电路结构，在许多电子设备和系统中具有重要的应用。

本文将介绍RC振荡电路的幅频特性和调节方法，以帮助读者更好地理解和应用此类电路。

一、RC振荡电路的基本原理与特性RC振荡电路是由电容器和电阻器组成的电路，通过其中的正反馈机制产生振荡现象。

其基本原理如下：1.1 电路结构RC振荡电路由电容器和电阻器组成，常见的结构有三种：串联结构、并联结构和串并联结构。

具体的电路连接方式会影响振荡电路的特性表现。

1.2 振荡原理RC振荡电路利用正反馈作用产生振荡。

当电荷通过电容器，经过电阻器放电时，电压下降导致电流变化。

通过反馈回路作用，电容器重新充电，并且周期性地产生振荡。

1.3 振荡频率RC振荡电路的振荡频率与电容器和电阻器的数值有关。

一般而言，振荡频率等于1/(2πRC)，其中R为电阻值，C为电容值。

1.4 幅频特性RC振荡电路的幅频特性反映了电压信号在不同频率下的衰减情况。

振荡电路在一定频率范围内，能够产生相对稳定的输出信号。

幅频特性曲线通常为低频段增益较高、高频段增益较低的形态。

二、RC振荡电路的调节方法为了满足不同的应用需求，人们通常需要对RC振荡电路的振荡频率和幅频特性进行调节。

以下是常用的调节方法：2.1 调节电容值通过改变电容器的数值，可以调节RC振荡电路的振荡频率。

增大电容值会降低振荡频率，而减小电容值会提高振荡频率。

如果需要实现精确的频率调节，可以使用可变电容器。

2.2 调节电阻值改变电阻器的数值可以对RC振荡电路的振荡频率进行调节。

增大电阻值会降低振荡频率，而减小电阻值会提高振荡频率。

调节电阻值通常会对幅频特性产生影响，需要综合考虑调节的效果。

2.3 加入补偿网络为了改善RC振荡电路的幅频特性，可以在电路中加入补偿网络。

补偿网络可以通过串联或并联的方式，优化电路的幅频特性。

例如，在串联结构中，可以加入并联的电容器或电感器来改变电路的频率响应。

一阶rc电路频率特性的研究实验报告实验目的：通过实验研究一阶RC电路的频率特性及其在不同频率下的相位和幅度变化规律。

实验原理：一阶RC电路，是由一个电阻和一个电容组成的电路，它可以用来对电路的输入信号进行滤波处理。

在此实验中，将对一阶RC电路的频率特性进行研究。

在一阶RC电路中，电容器与电阻器串联，构成了一个RC电路，其传递函数为H(jω)=-jωRC/(1-jωRC)。

通过对H(jω)进行分析，可得到该电路的幅频响应和相频响应。

电路的幅频响应表示在不同的频率下电路输入信号的振幅与输出信号的振幅之间的关系，而相频响应表示在不同频率下电路输入信号与输出信号之间的相位差。

实验设备：任意波形发生器、交流电桥、示波器、电阻器、电容器等。

实验步骤：1.搭建一阶RC电路，电阻值为1000Ω，电容值为0.01μF。

2.将任意波形发生器连接到电路的输入端，设置发生器输出为正弦波，频率范围为100Hz～100kHz，幅度为5V。

3.同时将电路的输出端连接到示波器，观察输出正弦波的幅度与相位随着不同频率的变化。

4.记录数据，绘制电路在不同频率下的幅频响应和相频响应曲线。

实验结果：通过实验可得到该一阶RC电路在不同频率下的幅频响应和相频响应曲线，如下图所示：（幅频响应曲线图）从图中可以看出，该一阶RC电路在低频时，输出信号的幅度很小，并且相位差比较大，而在高频时，输出信号的幅度逐渐增大，相位差逐渐变小，说明该电路具有滤波功能，在低频时可以起到削弱信号的作用，在高频时可以放大信号的作用。

结论：该实验通过对一阶RC电路的研究，得出了该电路在不同频率下的幅频响应和相频响应曲线，从中可以看出该电路具有滤波功能，且在不同的频率下表现不同的振幅和相位特性。

rc电路固有频率定义RC电路固有频率定义RC电路是由一个电阻和一个电容器组成的电路，在实际应用中，它被广泛地应用于各种类型的电子设备中。

RC电路具有许多特性，其中最重要的特性之一就是它的固有频率。

本文将详细介绍RC电路固有频率的定义、计算方法和相关知识点。

一、什么是RC电路固有频率？在RC电路中，当加入一个脉冲信号时，由于电容器会储存能量并随着时间逐渐释放，因此脉冲信号会在RC电路中发生衰减。

而这种衰减的速度与脉冲信号的频率密切相关。

当脉冲信号的频率等于RC电路的固有频率时，衰减速度最快，此时所得到的波形称为“共振波形”。

因此，我们可以将RC电路固有频率定义为：在一个给定的RC电路中，当输入信号与其本身产生共振时所对应的频率。

二、如何计算RC电路固有频率？在理论上，我们可以通过以下公式来计算任意一个给定的RC电路所对应的固有频率：f0 = 1 / (2πRC)其中，f0表示固有频率，R表示电阻的电阻值，C表示电容器的电容值。

这个公式是通过对RC电路进行数学模型建立和分析得到的。

三、RC电路固有频率的相关知识点1. RC电路固有频率与信号传输速度的关系在一个给定的RC电路中，当输入信号与其本身产生共振时所对应的频率是最高的。

而在其他频率下，信号将会被衰减。

因此，在RC电路中传输信号时，我们需要选择一个合适的输入频率来保证信号能够得到有效地传输。

2. RC电路固有频率与谐振现象当输入信号与RC电路固有频率相等时，我们会得到一种特殊的波形——共振波形。

这种波形具有较高的幅度和较长的持续时间，并且在实际应用中被广泛地应用于各种类型的设备中。

3. RC电路固有频率与带宽在实际应用中，我们通常需要将输入信号限制在一个特定范围内以保证设备能够正常工作。

而这个范围就称为带宽。

在RC电路中，带宽可以通过调整输入信号的频率来实现。

当输入信号的频率超过RC电路的固有频率时，信号将会被衰减，从而使得带宽变窄。

四、总结RC电路固有频率是指在一个给定的RC电路中，当输入信号与其本身产生共振时所对应的频率。

实验3 RC 网络频率特性研究一、实验原理1. 网络频率特性的定义网络的响应相量与激励相量之比是频率ω的函数，称为正弦稳态下的网络函数。

表示为 其模随频率ω变化的规律称为幅频特性，辐角随ω变化的规律称为相频特性。

为使频率特性曲线具有通用性，常以ω作为横坐标。

通常，根据随频率ω变化的趋势,将RC 网络分为“低通(LP )电路”、“高通(HP )电路”、“带通(BP )电路”、“带阻(BS )电路”等。

2．典型RC 网络的频率特性 (1) RC 低通网络图S3-1(a)所示为RC 低通网络。

它的网络函数为 其模为： 2)(11)(RC j H ωω+=辐角为： )arctan()(RC ωωϕ-= 显然，随着频率的增加， )(ωj H 将减小，这说明低频信号可以通过，高频信号被衰减或抑制。

当ω=1/RC ，即707.0/=i o U U ，通常把o U 降低到0.707 i U 时的角频率ω称为截止角频率C ω。

即(a) RC 低通网络 (b) 幅频特性 (c) 相频特性图S3-1 RC 低通网络及其频率特性(2) RC 高通网络图S3-2 (a)所示为RC 高通网络。

它的网络传递函数为 其模为： 2)1(11)(RCj H ωω+=辐角为：)arctan(90)(0RC ωωϕ-=可见，随着频率的降低而减小，说明高频信号可以通过，低频信号被衰减或抑制。

网络的截止频率仍为RC C /1=ω，因为ω=C ω时，|H(j ω)| =0.707。

它的幅频特性和相频特性分别如图S3-2(b)、(c)所示。

(a) RC 高通网络 (b) 幅频特性 (c) 相频特性图S3-2 RC 高通网络及其频率特性(3) RC 串并联网络（RC 带通网络）图S3-3(a)所示为RC 串并联网络。

其网络传递函数为 其模为： 2)1(91)(RCRC j H ωωω-+=辐角为： )31arctan()(RC RC ωωωϕ-=可以看出，当信号频率为RC C /1=ω时，模|H(j ω)| =1/3为最大,即输出与输入间相移为零。

一阶RC 电路频率特性的研究一阶RC 低通滤波器实验原理（1）一阶 RC 低通滤波器电路的频率特性实验图1是RC 串联电路，u i 是输入电压，u o 是输出电压。

u o 有效值的相量表示为电路的传递函数为101()()()1i U T j tg RC T j U j RC ωωωφωω-===-=∠+()T j ω=1()tg RCϕωω-=- Ci uou图1 低通滤波器电路0111111i i C i iC U U j C U Z U U R Z j C j RC R R j C j C ωωωωω====++++1f90--02f RCπ=00()1()0()0()-21()0.707()-24T j T j T j RC ωωϕωπωωϕωπωωωϕω====∞========时，，；时，，；时，；即传递函数是输出电压与输入电压有效值的比值，是角频率ω 的函数。

即当输出电压下降为输入电压的 70.7% 时，两者的相位差为- 45°，在实际应用中，为了不使输出电压下降过多，特规定此为最低限。

对应的0ω称为截止角频率，频率特性曲线如图2 所示。

由此可见，上述 RC 电路具有使 低频信号较易通过而抑制较高频率信号 的作用，故称为低通滤波电路。

即：该低通滤波电路的截止频率近似为1600HZ 。

000112=100=1F=11115921600221001f RC RCR C f RC ωπμππ==Ω⨯===≈⨯⨯⨯-6-6，，若电路器件的参数取：，10F（HZ ）10。