奥数容斥原理

小学奥数容斥原理教案【篇一：四年级奥数讲义：容斥原理(1)】四年级数学讲义奥数：容斥原理(1)教学目标：1、理解容斥原理，会画图分析其中关系，正确的找出答案。

2、培养学生的逻辑思维和数学思考能力。

3、培养学生良好的书写习惯。

一、教学衔接二、教学内容（一）知识介绍容斥问题涉及到一个重要原理——包含与排除原理，也叫容斥原理。

即当两个计数部分有重复包含时，为了不重复计数，应从它们的和中排除重复部分。

容斥原理：对n个事物，如果采用不同的分类标准，按性质a分类与性质b分类（如图），那么具有性质a或性质b的事物的个数=na＋nb－nab。

（二）例题精讲 nanb例1、一个班有48人，班主任在班会上问：“谁做完语文作业？请举手！”有37人举手。

又问：“谁做完数学作业？请举手！”有42人举手。

最后问：“谁语文、数学作业都没有做完？”没有人举手。

求这个班语文、数学作业都完成的人数。

【思路导航】完成语文作业的有37人，完成数学作业的有42人，一共有37＋42=79人，多于全班人数。

这是因为语文、数学作业都完成的人数在统计做完语文作业的人数时算过一次，在统计做完数学作业的人数时又算了一次，这样就多算了一次。

所以，这个班语文、数作业都完成的有：79－48=31人。

例2、某班有36个同学在一项测试中，答对第一题的有25人，答对第二题的有23人，两题都答对的有15人。

问多少个同学两题都答得不对？【分析与解答】已知答对第一题的有25人，两题都答对的有15人，可以求出只答对第一题的有25－15=10人。

又已知答对第二题的有23人，用只答对第一题的人数，加上答对第二题的人数就得到至少有一题答对的人数：10＋23=33人。

所以，两题都答得不对的有36－33=3人。

例3、某班有56人，参加语文竞赛的有28人，参加数学竞赛的有27人，如果两科都没有参加的有25人，那么同时参加语文、数学两科竞赛的有多少人？【分析与解答】要求两科竞赛同时参加的人数，应先求出至少参加一科竞赛的人数：56－25=31人，再求两科竞赛同时参加的人数：28＋27－31=24人。

點算的奧秘：容斥原理基本公式「容斥原理」(Principle of Inclusion and Exclusion)(亦作「排容原理」)是「點算組合學」中的一條重要原理。

但凡略為複雜、包含多種限制條件的點算問題，都要用到這條原理。

現在首先從一個點算問題說起。

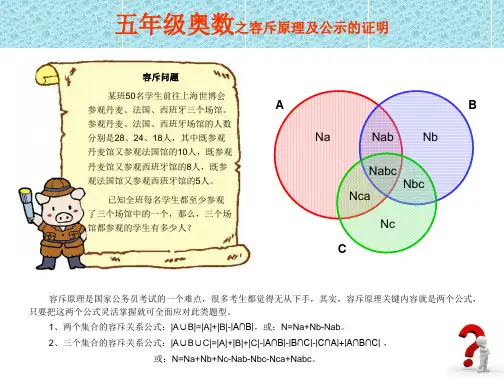
例題1：設某班每名學生都要選修至少一種外語，其中選修英語的學生人數為25，選修法語的學生人數為18，選修德語的學生人數為20，同時選修英語和法語的學生人數為8，同時選修英語和德語的學生人數為13 ，同時選修法語和德語的學生人數為6，而同時選修上述三種外語的學生人數則為3，問該班共有多少名學生？答1：我們可以把上述問題表達為下圖：其中紅色、綠色和藍色圓圈分別代表選修英語、法語和德語的學生。

根據三個圓圈之間的交叉關係，可把上圖分為七個區域，分別標以A至G七個字母。

如果我們用這七個字母分別代表各字母所在區域的學生人數，那麼根據題意，我們有以下七條等式：(1) A+D+E+G = 25；(2) B+D+F+G = 18；(3) C+E+F+G = 20；(4) D+G = 8； (5) E+G = 13；(6) F+G = 6；(7) G = 3。

現在我們要求的是A+B+C+D+E+F+G。

如何利用以上資料求得答案？把頭三條等式加起來，我們得到A+B+C+2D+2E+2F+3G = 63。

可是這結果包含了多餘的D、E、F和G，必須設法把多餘的部分減去。

由於等式(4)－(6)各有一個D、E和F，若從上述結果減去這三條等式，便可以把多餘的D、E和 F減去，得A+B+C+D+E+F = 36。

可是這麼一來，本來重覆重現的G卻變被完全減去了，所以最後還得把等式(7)加上去，得最終結果為A+B+C+D+E+F+G = 39，即該班共有39名學生。

□在以上例題中，給定的資料是三個集合的元素個數以及這些集合之間的交集的元素個數。

在該題的解答中，我們交替加上及減去這些給定的資料。

小学奥数容斥原理
小学奥数中的容斥原理是一种经典的数学方法，它常常用于解决有关组合计数的问题。

容斥原理可以帮助我们计算两个集合的交集、并集以及差集的元素个数。

具体来说，容斥原理告诉我们，要计算两个集合的并集的元素个数，我们可以先计算每个集合的元素个数，然后减去这两个集合的交集的元素个数。

这样可以避免重复计算。

例如，假设我们有两个集合A和B，集合A中有3个元素，集合B中有4个元素。

如果我们想计算这两个集合的并集的元素个数，根据容斥原理，我们应该先计算集合A的元素个数，再计算集合B的元素个数，然后减去集合A和集合B的交集的元素个数。

另外，容斥原理也可以用于计算三个集合的并集、四个集合的并集，以及更多集合的并集，只需要依次计算每个集合的元素个数，并根据公式依次加减交集的元素个数。

需要注意的是，在应用容斥原理时，我们需要确保计算交集和并集时没有重复计算的情况发生。

这需要我们对问题进行仔细分析和思考，以保证计算结果的正确性。

总之，容斥原理是一种解决组合计数问题的有力工具，在小学奥数中有着重要的应用，通过灵活运用容斥原理，我们可以更快、更准确地解决各类问题。

容斥原理森林中住着很多动物，据说狮子大王派仙鹤去统计鸟类的种数，蝙蝠跑过去对仙鹤说；“我有翅膀，我应该是属于鸟类的。

”于是仙鹤就把蝙蝠统计到鸟类的种类里去了，结果得出森林中一共有 80 种鸟类。

狮子大王又派大象去统计野兽的种类数，蝙蝠听说又来统计兽类了，急忙跑过去对大象说；“我没有羽毛，我应该是属于兽类的。

”于是大象就把蝙蝠统计到兽类的种类里去了，结果统计出森林中一共有 60 种兽类。

最后狮子大王问：“森林中共有鸟类和兽类多少种？”狡猾的狐狸听见了仙鹤和大象的统计结果，高兴地向狮子大王汇报：“这还不简单！森林中共有鸟类和兽类 140 种。

”这个统计正确吗？同学们肯定会说：“不对！蝙蝠被算了两次，应该再减去一，是 139 种。

”这个故事说明了一个数学问题，那就是被称为“容斥原理”的包含与排除问题。

当需要计数的两类事物互相包含（有部分重复交叉）时，应把重复计数的部分排除掉。

由此我们得到逐步排除法（容斥原理）：当两个计数部分有重复时，为了不重复计数，应从它们的和中减去重复部分。

容斥原理 1如果被计数的事物有 A、B 两类，那么， A 类 B 类元素个数总和= 属于 A 类元素个数+ 属于 B 类元素个数—既是 A 类又是 B 类的元素个数。

即A∪B = A+B - A∩B容斥原理 2如果被计数的事物有 A、B、C 三类，那么， A 类和 B 类和 C 类元素个数总和= A 类元素个数+ B 类元素个数+C 类元素个数—既是 A 类又是 B 类的元素个数—既是 A 类又是 C 类的元素个数—既是 B 类又是 C 类的元素个数+既是 A 类又是 B 类而且是 C 类的元素个数。

即A∪B∪C = A+B+C - A∩B - B∩C - C∩A +A∩B∩C容斥原理 1【例 1】★一次期末考试，某班有 15 人数学得满分，有 12 人语文得满分，并且有 4 人语、数都是满分，那么这个班至少有一门得满分的同学有多少人？【解析】依题意，被计数的事物有语、数得满分两类，“数学得满分”称为“A 类元素”，“语文得满分”称为“B 类元素”，“语、数都是满分”称为“既是 A 类又是 B 类的元素”，“至少有一门得满分的同学”称为“A 类和 B 类元素个数”的总和。

noi容斥原理
容斥原理，也称为包含-排除原理，是一种在组合数学和概率论中常用的计数方法。

它主要用于计算多个集合的交、并等运算的结果，尤其在处理有重叠部分的集合时非常有用。

NOI（全国青少年信息学奥林匹克竞赛）中，容斥原理也经常被用作解题的关键。

容斥原理的基本思想是通过两个或多个集合各自的元素个数和它们的交集个数来计算它们的并集个数。

具体地，如果有n个集合，那么这n个集合的并集中的元素个数等于这n个集合的元素个数之和，减去任意两个集合的交集的元素个数之和，再加上任意三个集合的交集的元素个数之和，以此类推，直到加上或减去所有n个集合的交集的元素个数。

在NOI中，容斥原理常常被应用于一些需要计算不同条件下的方案数的题目。

例如，给定一些限制条件，需要计算满足这些条件的整数对的个数。

这时，可以将每个限制条件看作一个集合，然后利用容斥原理计算满足所有条件的整数对的个数。

此外，容斥原理还可以用于计算一些组合数学中的问题，如计算一个集合的子集的个数、计算一个图的边的个数等。

需要注意的是，在使用容斥原理时，需要注意集合之间的关系和顺序，以避免重复计算或遗漏计算。

同时，也需要灵活运用容斥原理，根据题目的具体情况进行调整和变形。

总之，容斥原理是一种非常有用的计数方法，在NOI等数学竞赛中经常被应用。

通过熟练掌握容斥原理的思想和应用方法，可以更好地解决一些复杂的计数问题。

容斥原埋在很多计数问题中常用到数学上的一个包含与排除原理，也称为容斥原理.为了说明这个原理，我们先介绍一些集合的初步知识。

例1、桌上有两张圆纸片A、B.假设圆纸片A的面积为30平方厘米，圆纸片B的面积为20平方厘米.这两张圆纸片重叠部分的面积为10平方厘米.则这两张圆纸片覆盖桌面的面积由容斥原理的公式（1）可以算出为：｜A∪B｜=30＋20-10＝40（平方厘米）。

例2、求在1至100的自然数中能被3或7整除的数的个数。

分析解这类问题时首先要知道在一串连续自然数中能被给定整数整除的数的个数规律是：在n个连续自然数中有且仅有一个数能被n整除.根据这个规律我们可以很容易地求出在1至100中能被3整除的数的个数为33个，被7整除的数的个数为14个，而其中被3和7都能整除的数有4个，因而得到解：设A=｛在1～100的自然数中能被3整除的数｝，B＝｛在1～100的自然数中能被7整除的数｝，则A∩B=｛在1～100的自然数中能被21整除的数｝。

∵100÷3＝33…1，∴｜A｜＝33。

∵100÷7＝14…2，∴｜B｜=14。

∵100÷21＝4…16，∴｜A∩B｜=4。

由容斥原理的公式（1）：｜A∪B｜＝33＋14-4=43。

答：在1～100的自然数中能被3或7整除的数有43个。

例3、求在1～100的自然数中不是5的倍数也不是6的倍数的数有多少个？分析如果在1～100的自然数中去掉5的倍数、6的倍数，剩下的数就既不是5的倍数也不是6的倍数，即问题要求的结果。

解：设A＝｛在1～100的自然数中5的倍数的数｝，B=｛在1～100的自然数中6的倍数的数｝，数.为此先求｜A∪B｜。

∵100÷50=20，∴｜A｜=20又∵100÷6＝16…4，∴｜B｜=16∵100÷30＝3…10，∴｜A∩B｜=3，｜A∪B｜=｜A｜+｜B｜-｜A∩B｜=20＋16-3＝33。

小学奥数之容斥原理知识点容斥原理容斥问题涉及到一个重要原理——包含与排除原理，也叫容斥原理。

即当两个计数部分有重复包含时，为了不重复计数，应从它们的和中排除重复部分。

容斥原理：对n个事物，如果采用不同的分类标准，按性质a分类与性质b分类（如图），那么具有性质a或性质b 的事物的个数=Na＋Nb－Nab。

例1：一个班有48人，班主任在班会上问：“谁做完语文作业？请举手！”有37人举手。

又问：“谁做完数学作业？请举手！”有42人举手。

最后问：“谁语文、数学作业都没有做完？”没有人举手。

求这个班语文、数学作业都完成的人数。

分析与解答：完成语文作业的有37人，完成数学作业的有42人，一共有37＋42=79人，多于全班人数。

这是因为语文、数学作业都完成的人数在统计做完语文作业的人数时算过一次，在统计做完数学作业的人数时又算了一次，这样就多算了一次。

所以，这个班语文、数作业都完成的有：79－48=31人。

例2：某班有36个同学在一项测试中，答对第一题的有25人，答对第二题的有23人，两题都答对的有15人。

问多少个同学两题都答得不对？分析与解答：已知答对第一题的有25人，两题都答对的有15人，可以求出只答对第一题的有25－15=10人。

又已知答对第二题的有23人，用只答对第一题的人数，加上答对第二题的人数就得到至少有一题答对的人数：10＋23=33人。

所以，两题都答得不对的有36－33=3人。

例3：某班有56人，参加语文竞赛的有28人，参加数学竞赛的有27人，如果两科都没有参加的有25人，那么同时参加语文、数学两科竞赛的有多少人？分析与解答：要求两科竞赛同时参加的人数，应先求出至少参加一科竞赛的人数：56－25=31人，再求两科竞赛同时参加的人数：28＋27－31=24人。

例4：在1到100的自然数中，既不是5的倍数也不是6的倍数的数有多少个？分析与解答：从1到100的自然数中，减去5或6的倍数的个数。

从1到100的自然数中，5的倍数有100÷5=20个，6的倍数有16个（100÷6=16……4），其中既是5的倍数又是6的倍数（即5和6的公倍数）的数有3个（100÷30=3……10）。

容斥原理森林中住着很多动物，据说狮子大王派仙鹤去统计鸟类的种数，蝙蝠跑过去对仙鹤说；“我有翅膀，我应该是属于鸟类的。

”于是仙鹤就把蝙蝠统计到鸟类的种类里去了，结果得出森林中一共有 80 种鸟类。

狮子大王又派大象去统计野兽的种类数，蝙蝠听说又来统计兽类了，急忙跑过去对大象说；“我没有羽毛，我应该是属于兽类的。

”于是大象就把蝙蝠统计到兽类的种类里去了，结果统计出森林中一共有 60 种兽类。

最后狮子大王问：“森林中共有鸟类和兽类多少种？”狡猾的狐狸听见了仙鹤和大象的统计结果，高兴地向狮子大王汇报：“这还不简单！森林中共有鸟类和兽类 140 种。

”这个统计正确吗？同学们肯定会说：“不对！蝙蝠被算了两次，应该再减去一，是 139 种。

”这个故事说明了一个数学问题，那就是被称为“容斥原理”的包含与排除问题。

当需要计数的两类事物互相包含（有部分重复交叉）时，应把重复计数的部分排除掉。

由此我们得到逐步排除法（容斥原理）：当两个计数部分有重复时，为了不重复计数，应从它们的和中减去重复部分。

容斥原理 1如果被计数的事物有 A、B 两类，那么， A 类 B 类元素个数总和= 属于 A 类元素个数+ 属于 B 类元素个数—既是 A 类又是 B 类的元素个数。

即A∪B = A+B - A∩B容斥原理 2如果被计数的事物有 A、B、C 三类，那么， A 类和 B 类和 C 类元素个数总和= A 类元素个数+ B 类元素个数+C 类元素个数—既是 A 类又是 B 类的元素个数—既是 A 类又是 C 类的元素个数—既是 B 类又是 C 类的元素个数+既是 A 类又是 B 类而且是 C 类的元素个数。

即A∪B∪C = A+B+C - A∩B - B∩C - C∩A +A∩B∩C容斥原理 1【例 1】★一次期末考试，某班有 15 人数学得满分，有 12 人语文得满分，并且有 4 人语、数都是满分，那么这个班至少有一门得满分的同学有多少人？【解析】依题意，被计数的事物有语、数得满分两类，“数学得满分”称为“A 类元素”，“语文得满分”称为“B 类元素”，“语、数都是满分”称为“既是 A 类又是 B 类的元素”，“至少有一门得满分的同学”称为“A 类和 B 类元素个数”的总和。

容斥原理在计数时，为了使重叠部分不被重复计算，人们研究出一种新的计数方法，这种方法的基本思想是：先不考虑重叠的情况，把包含于某内容中的所有对象的数目先计算出来，然后再把计数时重复计算的数目排斥出去，使得计算的结果既无遗漏又无重复，这种计数的方法称为容斥原理。

容斥原理（1）如果被计数的事物有A、B两类，那么，A类或B类元素个数= A类元素个数+B类元素个数—既是A类又是B类的元素个数。

例1一次期末考试，某班有15人数学得满分，有12人语文得满分，并且有4人语、数都是满分，那么这个班至少有一门得满分的同学有多少人？分析：依题意，被计数的事物有语、数得满分两类，“数学得满分”称为“A类元素”，“语文得满分”称为“B类元素”，“语、数都是满分”称为“既是A类又是B类的元素”，“至少有一门得满分的同学”称为“A类或B类元素个数”的总和。

试一试：某班学生每人家里至少有空调和电脑两种电器中的一种，已知家中有空调的有41人，有电脑的有34人，二者都有的有27人，这个班有学生多少人？（并说一说你的想法。

）容斥原理（2）如果被计数的事物有A、B、C三类，那么，A类或B类或C类元素个数= A类元素个数+B类元素个数+C类元素个数—既是A类又是B类的元素个数—既是A类又是C类的元素个数—既是B类又是C类的元素个数+既是A类又是B类而且是C类的元素个数1、某艺术团的小演奏家们每人都至少会演奏小提琴和钢琴中的一种。

他们中有32人会拉小提琴，27人会弹钢琴，小提琴和钢琴都能演奏的有11人。

这个团共有多少个小演奏家？2、一个班有学生42人，参加体育队的有30人，参加文艺队的有25人，并且全班每人至少参加一个队。

问：这个班两队都参加的有多少人？3、京华小学五年级学生采集标本。

采集昆虫标本的有25人，采集植物标本的有19人，两种标本都采集的有8人。

全班学生共有40人，没有采集标本的有多少人？4、有100位旅客，其中有10人既不懂英语又不懂日语，有75人懂英语，83人懂日语。

容斥原理学生姓名授课日期教师姓名授课时长知识定位容斥原理中的知识点比较简单，是计数问题中比较浅的一支。

这个知识点经常和数论知识结合出综合型题目。

这个原理本身并不是很难理解，不过经常和数论知识结合出题，所以对学生的理解层次要求较高，学生必须充分理解、吃透。

1.充分理解和掌握容斥原理的基本概念2.利用图形分析解决容斥原理问题知识梳理授课批注：本讲的知识点必须让学生充分理解、吃透，这个原理本身并不是很难理解，不过经常和数论知识结合出题所以对学生的理解层次要求较高。

一. 容斥原理的概念定义在一些计数问题中，经常遇到有关集合元素个数的计算。

我们用|A|表示有限集A 的元素个数。

求两个集合并集的元素的个数，不能简单地把两个集合的元素个数相加，而要从两个集合个数之和中减去重复计算的元素个数，即减去交集的元素个数，用式子可表示成：|A∪B| = |A| + |B| - |A∩B|，我们称这一公式为包含与排除原理，简称容斥原理。

图示如右:A表示小圆部分，B表示大圆部分，C表示大圆与小圆的公共部分，记为：A∩B，即阴影面积。

用法：包含与排除原理告诉我们，要计算两个集合A、B的并集A∪B的元素的个数，可分以下两步进行：第一步：分别计算集合A、B的元素个数，然后加起来，即先求|A|+|B|（意思是把A、B的一切元素都“包含”进来，加在一起）；第二步：从上面的和中减去交集的元素个数，即减去C=|A∩B|（意思是“排除”了重复计算的元素个数）二.竞赛考点1.容斥原理的基本概念2.与数论相结合的综合型题目例题精讲【试题来源】【题目】在一个炎热的夏日，10个小学生去冷饮店每人都买了冷饮。

其中6人买了汽水，6人买了可乐，4人买了果汁，有3人既买了汽水又买了可乐，1人既买了汽水又买了果汁，2人既买了可乐又买了果汁。

问：(1)三样都买的有几人？(2)只买一样的有几人？【答案】0,4【解析】(1)设三样都买的学生有a人，那么6+6+4-3-1-2+a=10，解得a=0，所以没有人三种东西都买了.(2)去冷饮店的学生中除了买一样的外，只有买两样东西的，因为买两样东西的有3+1+2=6(人)，所以买一样东西的学生有10-6=4(人).【知识点】容斥原理【适用场合】当堂例题【难度系数】3【试题来源】【题目】某班有学生46人，在调查他们家中是否有电子琴和小提琴时发现，有电子琴的22人，两种琴都没有的14人，只有小提琴的与两种琴都有的人数之比是5∶3。

小学奥数之容斥原理容斥原理例1：给定长8厘米，宽6厘米的长方形和边长5厘米的正方形，求这两个图形覆盖桌面的面积。

分析与解：两个图形的重叠部分是一个直角三角形，可以用三种方法求出它的面积：方法一：方法二：方法三：最终答案为67平方厘米。

例2：六一班共有26名学生参加了无线电小组和航模小组，其中有17人参加了无线电小组，14人参加了航模小组，有多少人参加了两个小组？分析与解：如果直接将17人和14人相加，会把两个小组都参加的人算两次，因此需要用容斥原理来计算。

具体地，两个小组都参加的人数等于总人数减去只参加一个小组的人数：另一种方法是：最终答案为5人。

例3：六一班共有46名学生，其中19人会骑自行车，25人会游泳，7人既会骑车又会游泳，有多少人既不会骑自行车也不会游泳？分析与解：首先计算会骑车或会游泳的人数，然后减去既会骑车又会游泳的人数，就得到了既不会骑车也不会游泳的人数：最终答案为9人。

例4：某年级的课外小组分为美术、音乐、手工三个小组，参加美术小组有20人，参加音乐小组有24人，参加手工小组有31人，同时参加美术和音乐两个小组的有5人，同时参加音乐和手工两个小组的有6人，同时参加美术和手工两个小组的有7人，三个小组都参加的有3人，这个年级参加课外小组的同学共有多少人？分析与解：用容斥原理计算总人数，需要减去重复多余的部分。

具体地，先计算参加至少一个小组的人数，然后减去同时参加两个小组的人数，再加上同时参加三个小组的人数：最终答案为60人。

例5：某班有若干学生参加了短跑、投掷和跳远三项检测，其中有4人三项都未达到优秀，其他人至少有一项是优秀。

给定各项检测中达到优秀的人数，求全班人数。

分析与解：用容斥原理计算全班人数，需要减去三项都未达到优秀的人数。

具体地，先计算跑、跳、投至少有一项达到优秀的人数，然后加上三项都未达到优秀的人数：最终答案为42人。

例6：求分母为105的最简真分数的个数。

分析与解：分母为105的最简真分数，可以表示成$a/105$ 的形式，其中 $a$ 是比105小的正整数，且 $a$ 和105互质。

五年级奥数容斥问题：容斥原理（1）如果被计数的事物有a、b两类，那么，a类或b类元素个数= a类元素个数+b类元素个数—既是a类又是b类的元素个数。

容斥原理（2）如果被计数的事物有a、b、c三类，那么，a类或b类或c类元素个数= a类元素个数+b类元素个数+c类元素个数—既是a类又是b类的元素个数—既是a类又是c类的元素个数—既是b类又是c类的元素个数+既是a类又是b类而且是c类的元素个数1、艺术小学举行学生画展，其中18幅画不是六年级的，20幅画不是五年级的，现在知道五、六年级共展出22幅画。

问其他年级展出多少幅？分析：18幅不是六年级，那就是五年级和其他年级的，20幅不是五年级，就是六年级和其他年级，已知五六年级展出22幅，所以其他年级展出就是八幅。

（18+20-22）/2=8（幅）2、某地区100个外语教师中，每人至少懂英语和日语中的一种语言。

已知懂英语的75人，懂日语的有45人。

问只懂英语的有几人？分析；两种语言都懂的人为；懂英语的和懂日语和减外语教师总数。

只懂英语的就是75减两种都懂得了。

75+45-100=20（人）75-20=55（人）3、在1至100的整数中,能被2整除或能被3整除的数共有几个?分析：100中，能被2整除的有100/2=50个，能被3整除的有100/3=33个，同时能被2和3整除的100/6=16个，注意这16个包括在能被2和3整除的，要去掉。

就是100内能被或3整除的。

50+33-16=67个4、全班50人，不会骑自行车的有23人，不会滑旱冰的有35人，两样都会的有4人，两样都不会的有多少人？分析：骑自行车：27人会滑旱冰：15人都会：4人都不会的：50-（27+15-4）=12人画个图就可以看出来了，4个人是多加的，所以要减去。

5、六年级有52人，其中喜欢绘画的36人，喜欢书法的有42人，喜欢唱歌的有48人，喜欢跳舞的有34人，这个班最少有多少学生对这四项活动都喜欢？分析：52-36=16个人不喜欢绘画，52-42=10个人不喜欢书法，52-48=4个人不喜欢唱歌，52-34=18个人不喜欢跳舞。

(奥数典型题)容斥原理--2024年六年级下册小升初数学思维拓展容斥原理【知识点归纳】在日常生活中，人们常常需要统计一些数量，在统计的过程中，往往会发现有些数量重复出现，为了使重复出现的部分不致被重复计算，人们研究出一种新的计数方法，既先不考虑重复的情况，把包含于某内容中的所有对象的数目先计算出来，然后再把计数时重复计算的数目排除出去，使计算的结果既无遗漏又无重复．这种计数方法称为包含排除法，也叫做容斥原理或重叠问题．一般方法：在解答有关包含排除问题时，我们常常利用圆圈图（韦恩图）来帮助分析思考．容斥原理1：两量重叠问题A类与B类元素个数的总和＝A类元素的个数+B类元素个数﹣既是A类又是B类的元素个数用符号可表示成：A∪B＝A+B﹣A∩B（其中符号“∪”读作“并”，相当于中文“和”或者“或”的意思，符号“∩”读作“交”，相当于中文“且”的意思）．容斥原理2：三量重叠问题A类、B类与C类元素个数的总和＝A类元素的个数+B类元素个数+C类元素个数﹣既是A类又是B类的元素个数﹣既是B类又是C类的元素个数﹣既是A类又是C类的元素个数+同时是A类、B类、C类的元素个数．用符号表示为：A∪B∪C＝A+B+C﹣A∩B﹣B∩C﹣A∩C+A∩B∩C1．三年级共有80名同学参加书法兴趣小组和美术兴趣小组，其中参加书法组的有52人，参加美术组的有48人．那么，既参加书法组又参加美术组的有多少人？2．我们班参入调查了饭后吃水果情况：30人喜欢吃苹果，27人喜欢吃梨，10人两种都喜欢，问我们班有多少人？3．同学们收集图片．张明、李红、蔡正明、王丹、熊威、高伟、梅芳7个人收集了名山图片，吴凤、李红、王丹、戴月红、高伟这5人收集了河流图片，吴心怡、张冬、李可这3人收集了奥运图片．（1）收集名山图片和奥运图片的共有多少人？（2）收集名山图片和河流图片的共有多少人？4．在校运动会上，共有30人参加跳远和跳高。

参加跳远的有18人，参加跳高的有22人，既参加跳远又参加跳高的有多少人？5．三（1）班有48人，其中订《少年报》的有32人，订《数学报》的有38人，有25人两份报都订。

第35周容斥问题专题简析:容斥问题涉及一个重要原理一一包含与排除原理，也叫容斥原理。

当两个计数部分有重复包含时，为了不重复地计数，应从它们的和中排除重复部分。

容斥原理:对n个事物，如果采用两种不同的分类标准,按性质a分类与性质b分类(如右图所示),那么具有性质a或性质b的事物的个数是Na 十Nb- Nab。

例1：一个班有48人，班主任在班会上问“谁做完语文作业了?请举手！”有37人举手。

又问:“谁做完数学作业了?请举手!”有42人举手。

最后问“谁语文、数学作业都没有做完?“没有人举手。

求这个班语文、数学作业都完成的人数。

练习一：1、五年级有122 名学生参加语文、数学考试，每人至少有一门功课取得优秀成绩。

其中语文成绩优秀的有65 人，数学成绩优秀的有87 人。

语文、数学成绩都优秀的有多少人?2、四(1)班有54 人，订阅<小学生优秀作文》和(数学大世界)两种读物的有13 人，订《小学生优秀作文》的有45 人，每人至少订种读物。

订《数学大世界》》的有多少人?3、学校文艺组每人至少会演奏一种乐器，已知会拉手风琴的有24人，会弹电子琴的有17人，其中两种乐器都会演奏的有8人。

这个文艺组一共有多少人?例2：城中小学选出10名学生参加区作文和数学比赛，结果每人都获奖。

其中有3人两项比赛都获奖，作文比赛获奖的有5 人,求数学比赛获奖的有多少人?练习：1、一个班有55 名学生，他们分别订阅了《小学生数学报》和《中国少年报》。

其中订阅《小学生数学报》的有32 人,两种报纸都订阅的有15 人,求订阅《中国少年报》的有多少人?2、四(1)班有40 个学生,有19 人参加了数学和科技两个兴趣小组。

其中有11人两个小组都没参加，有25人参加数学小组，求有多少人参加了科技小组?3、在四年级96 个学生中调查会下中国象棋和围棋的人数。

调查结果显示:有78人会下中国象棋，有24 人两样都会，还有12人两样都不会。

求会下围棋的有多少人?例3：某班有56人，参加语文竞赛的有28人，参加数学竞赛的有27人，如果两科都没有参加的有25人，那么同时参加语文、数学两科竞赛的有多少人?练习：1、一个旅行社有36 人，其中会英语的有24 人,会法语的有18 人,两样都不会的有4 人。

容斥原理专题简析：容斥问题涉及到一个重要原理——包含与排除原理，也叫容斥原理。

即当两个计数部分有重复包含时，为了不重复计数，应从它们的和中排除重复部分。

容斥原理：对n个事物，如果采用不同的分类标准，按性质a分类与性质b分类（如图），那么具有性质a或性质b的事物的个数=N a＋N b－N ab。

Nab NbNa例1：一个班有48人，班主任在班会上问：“谁做完语文作业请举手！”有37人举手。

又问：“谁做完数学作业请举手！”有42人举手。

最后问：“谁语文、数学作业都没有做完”没有人举手。

求这个班语文、数学作业都完成的人数。

分析完成语文作业的有37人，完成数学作业的有42人，一共有37＋42=79人，多于全班人数。

这是因为语文、数学作业都完成的人数在统计做完语文作业的人数时算过一次，在统计做完数学作业的人数时又算了一次，这样就多算了一次。

所以，这个班语文、数作业都完成的有：79－48=31人。

练习一1，五年级有122名学生参加语文、数学考试，每人至少有一门功课取得优秀成绩。

其中语文成绩优秀的有65人，数学优秀的有87人。

语文、数学都优秀的有多少人2，四年级一班有54人，订阅《小学生优秀作文》和《数学大世界》两种读物的有13人，订《小学生优秀作文》的有45人，每人至少订一种读物，订《数学大世界》的有多少人3，学校文艺组每人至少会演奏一种乐器，已知会拉手风琴的有24人，会弹电子琴的有17人，其中两种乐器都会演奏的有8人。

这个文艺组一共有多少人例2：某班有36个同学在一项测试中，答对第一题的有25人，答对第二题的有23人，两题都答对的有15人。

问多少个同学两题都答得不对分析与解答：已知答对第一题的有25人，两题都答对的有15人，可以求出只答对第一题的有25－15=10人。

又已知答对第二题的有23人，用只答对第一题的人数，加上答对第二题的人数就得到至少有一题答对的人数：10＋23=33人。

所以，两题都答得不对的有36－33=3人。