七年级数学下册 5.4.1 平移(第2课时)导学案(无答案)(新版)新人教版

5.4平移【学习目标】1.了解平移的概念，会进行点的平移；理解平移的性质，能解决简单的平移问题。

2.培养空间观念和变换思想，学会用运动的观点分析问题。

【前置学习】一、问题引领观察下列生活中的运动情景，它们的运动方式有什么共同特点？1.推开窗户；2.拉开抽屉；3.飞机直飞；4.电梯升降。

二、自主学习回答下列问题。

1.观察思考：仔细观察课本P28图5.4-1中图案，它们有什么共同特点？能否根据其中的一部分绘制出整个图案？若称这一部分为“基本图形”，请在这三幅图案中分别描出它们的“基本图形”。

2．绘图探究：（1）在一张半透明的纸上划一条直线，在直线上取A、A′、A〞三点，然后将半透明的纸盖在课本图5.4-2的雪人上，使雪人的鼻尖对准A点，先描出一个雪人，再将半透明的纸沿着这条直线移动，使雪人的鼻尖分别对准A′、A〞点再描出两个雪人。

（2）在所画出的相邻两个雪人中,找出三组对应点:鼻尖A与A′,帽顶B与B′,纽扣C与C′,连接这些对应点:AA′、BB′、CC′。

观察这些线段,它们的位置关系如何?再量一量它们的长短，数量关系又如何？（3）在另外两个雪人中再连接一些其它对应点的线段，是否有类似的位置、数量关系？3.总结规律：（1）平移的定义：将一个图形沿方向移动，图形的这种移动叫做平移。

图形的平移是由和决定的。

（2）平移性质：平移不改变图形的和，只改变图形的。

平移前后图形中对应线段的大小，对应角的大小。

连接各组对应点的线段的位置关系是，大小关系是。

三、疑难摘要（记下你的疑难与困惑，在课堂上交流解决）。

【学习探究】一、合作交流、解决困惑1.小组交流：通过自学你学会了什么？还有什么问题不明白？互相解答存在的困惑。

2.班级展示与教师点拔：展示一：（1）如图,△FDE经过怎样的平移可得到△ABC？（2）下列说法正确的是（）（A）平移能改变图形的位置及形状（B）平移的方向要么水平要么竖直（C）平移中，连接对应点的线段一定平行（D）平移中，连接对应点的线段一定相等展示二：（教师根据学生情况自主生成）二、应用新知、解决问题例如图，网格中有△ABC，请作出将△ABC向上平移2个单位再向右平移3个单位长度的图形。

《5.4平移》导学案班级______ 小组_____ 姓名_______ 评价 ____一、学习目标1. 通过实例理解平移的定义，掌握平移的性质，会画简单图形和经过平移后的图形；2. 经历探索图形平移的性质的过程以及与他人合作交流的过程，进一步发展空间观念;3. 保持热情，高效学习。

二、自主学习1. 阅读教材第28页…29页上半部分，学习“平移”的定义：在平面内，将一个图形整体沿某一方向移动一定的距离，这样的图形移动叫做平移变换，简称平移。

比如：在铁轨上行驶的火车、在跑道上加速行驶的飞机、____________ : 2. 平移的性质；（1）把一个图形整体沿某一直线方向移动，会得到一个新的图形，新的图形与原图形的_______ 与_______ 完全相同；（2）新图形中的每一点，都是原图形中的某一个点移动得到的，这两个点是____________ （3）_________________________________ 连接各组对应点的线段o3. 平移的两个要素：（1）平移的方向；（2）平移的 ______ -4. 阅读教材第29页“例”，学习用平移的方法作图。

5. 例题学习：如图，用平移的方法说明怎样得出平行四边形的面积公式S=ah o解：如左图，平行四边形的一边长是a,这条边上的高是h,它的面积是s=aho为什么呢？将高线所截得的直角三角形向右平移至右图。

得长方形，它的两邻边分别是a和h,它的面积是S=ah,而左图的平行四边形的血积与右图长方形面积相等。

所以平行四边形的血积公式S=ahg三、合作与探究1. 急刹车时，汽车在地面上运动，可以看做_______ ；2. 若线段EF是经过线段AB平移得到的，泽EF与AB的关系 __________3.图形经过平移后，______ 图形的位置， _____ 图形的形状， ___ 图形的大小。

（填“改变”或“不改变”）;4. 经过平移，每一组对应点所连成的线段 _________5. 如图，ADEF平移得到△ABC,则平移方向是_______ ,平移的距离是 _______ ，若ZB=3»° ,ZF=7»°则ZA二_____6. _________________________________ 如图所示，整个图形能通过图案平移次而得到的。

5.4平移的导学案班级：姓名：主备人：审核人：【学习目标】1．理解平移的概念。

2．掌握平移的性质。

3．懂得画平移图像。

【学习重难点】：平移的性质以及画平移图像。

【课前预习】自学课本第28—30页的内容，并完成导学案上的习题。

【教学过程】一、知识链接：1、思考：仔细观察课本图5.4-1的一些美丽的图案，他们有什么共同的特点，能否根据其中一部分绘制出整个图案？2、（看多媒体展示图）传送带上的电视机的形状大小在运送过程中发生了什么变化？3、（看多媒体展示图）电梯在运行过程中，每一梯阶发生了怎样的变化？二、合作探究（一）：1、如何在一张纸上画出一排形状、大小都一样的雪人呢？（课本图5.4-2）方法：2、在所画出的相邻两个雪人中，找出三组对应点（例如，它们的鼻尖A与A′，帽顶B与B′，纽扣C与C′），连接这些对应点，观察得出的线段，它们的位置、长短有什么关系？答：3、请你在作出连接其他对应点的线段，它们是否仍有前面的关系？（）练习（一）：△ABC沿着射线XY的方向平移一定距离后成为△ABC。

画出图形，并找出图中平行且相等的三条线段合作探究（二）：1、在平面内，一个图形沿某个方向移动一定的距离，这种图形的变换叫做 。

上面图形上的一点A 平移后成为点A ’，这样的两点叫做 ，线段AB 和线段A ’B ’叫做 ，∠A 和∠A ’叫做 。

2、平移的性质：（1）平移只改变图形的位置，不改变图形的形状和大小；（2）连接对应点的线段平行（或共线）且相等．（3）对应线段平行且相等，对应角相等。

例1:如右图，平移线段AB ，使点A 移动到点A ′。

画出平移后的线段A ′B ′例 2:（课本56页图5.4-6（1）） 经过平移，三角形ABC 的顶点A移到了点 D ． 画出平移后的三角形A ˊB ˊC ˊ．（画在课本上）练习（二）：1、在下面的六幅图案中，（2）（3）（4）（5）（6）中的哪个图案可以通过平移图案（1）得到？（ ）2、下面 2，3，4，5 幅图中那幅图是由1平移得到的？3、将图中的小船向左平移四格（多媒体展示）4、在以下生活现象中,不是平移现象的是（ ）A. 站在运动着的电梯上的人B. 左右推动的推拉窗扇C. 小李荡秋千运动D. 躺在火车上睡觉的旅客2 3 4 51 BA B A ,三、巩固提高：1、如图所示,△ABC平移到△A′B′C′的位置,则点A的对应点是____,点B的对应点是____，点C的对应点是____。

5.4 平移德育目标：观察、归纳、推理对数学知识中获取数学猜想和论证的重要作用，在独立思考和小组交流中学习。

学习目标：1、了解平移的概念，会进行点的平移；2、理解平移的性质，能解决简单的平移问题.学习重点：平移的概念和作图方法学习难点：平移的作图学习过程：一、课堂引入：（知识复习）观察课本图形,我们发现他们都有一个局部和其他部分重复,如果给你一个局部,你能复制他们吗?如何在一张半透明的纸上，画出一排形状和大小如图的雪人？二、自学课本：预习课本P28—P30，并完成以下练习1.在平面内，将一个图形沿某个方向＿＿＿一定的距离，这样的图形运动称为平移，平移改变的是图形的＿＿＿＿＿。

平移不改变图形的＿＿＿＿和＿＿＿＿。

2.图形的平移是由＿＿＿＿＿和＿＿＿＿＿决定的。

辅导教师:发现学生在看书过程中没有发现结论的,教师给以引导.3.经过平移所得的图形与原来的图形的对应线段＿＿＿＿＿＿＿，对应角＿＿＿＿，对应点所连的线段＿＿＿＿。

三、自学例题例: 如图,(1)平移三角形ABC,使点A运动到A`,画出平移后的三角形A`B`C`.辅导教师:观察学生的作图,在学生不当的地方给予指导.四、当堂练习。

（学生活动：先进行小组讨论，然后独立完成，再进行小组交流和评价）（A组）1．下列生活中的现象,不属于平移的是( )A.电梯上的人B.铝合金门窗的移动C．工厂里传输带上的物品 D.下雨天汽车的雨刷2．△FDE经过怎样的平移可得到△ABC.( )A.沿射线EC的方向移动DB长;B.沿射线EC的方向移动CD长C.沿射线BD的方向移动BD长;D.沿射线BD的方向移动DC长3．平移后的图形与原图形_____、______完全相同，新图形中的每一个点，都是由___________________移动后得到的，这两个点是对应点，连接各组对应点的线段______且________或__________。

对应线段______且________或__________。

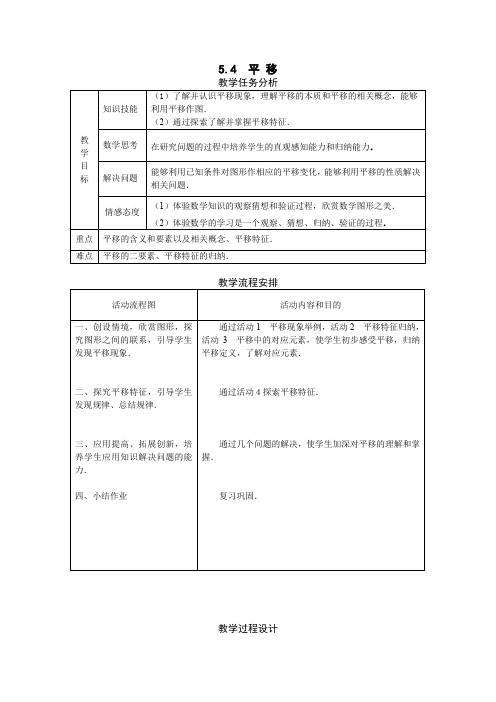
5.4 平移教学过程设计一、创设情境，欣赏图形，探究图形之间的联系，引导学生发现平移现象． 活动1举出生活中的平移的现象：火车、电梯、飞机等，并用计算机演示． 学生倾听、理解、想象和欣赏． 活动2问题1：请你举出一些生活中的平移现象． 问题2：什么样的变化才是平移？ 学生活动设计：学生可以分组讨论，举例，其他人辨别是否是平移现象，然后通过自己举的事例来归纳和总结平移的含义．学生归纳：平移：图形的平行移动就是平移． 大小和方向都不变． 决定因素：方向和距离．让学生充分讨论，辨别自己的判断，同学间进行交流． 活动3把一个三角形ABC ，移到三角形A ′B ′C ′的位置．你能理解下列概念吗？ （1）对应点；（2）对应线段． 学生活动设计：学生观察图形，可以发现经过平移能够互相重合的点就是对应点，对应点的连线就是对应线段． 教师活动设计：教师在此环节主要让学生学会观察，学会分析两个图形之间的关系，引导学生发现经过变换后能够互相重合的元素就是对应元素．因此，上述平移中，对应点是A 与A ′，B 与B ′，C 与C ′；对应线段是AB 与A ′B ′，BC 与B ′C ′，AC 与A ′C ′． 二、探究平移特征，引导学生发现规律、总结规律． 活动4如图△ABC 经过平移成为△A ′B ′C ′，在这个变化过程中，你能得到哪些量是不变的？除了这些量不变外，你还能发现哪些结论？学生活动设计： 学生通过画图、度量进行猜测，得出下列结论 结论：1． 对应线段平行且相等；（相等、平行因为是平移，是图形的平行移动）；2．对应点所连线段平行且相等（都是平移的距离）． 教师活动设计：此时要鼓励学生大胆猜测，引导学生归纳出平行的特征．三、应用提高、拓展创新，培养学生应用知识解决问题的能力． 问题1：如图，△ABC 平移到△A ′B ′C ′的位置． （1）请指出平移的距离和方向．（2）点D 、E 、F 经过平移到了什么位置？C'C'B'问题2：如图，将△ABC先下移2个格再右移4个格得到△A′B′C′．问题3：图案设计，根据如图所示的图形，通过平移设计一个图案．学生活动设计：以上三个问题，由学生自主探索，自主设计，找到解决问题的方法，从而进一步体会平移在作图中的应用，同时感受平移变化的特征．教师活动设计：鼓励学生解决问题，在进行图案设计时，鼓励学生充分发挥自己的想象力．〔解答〕．问题1（1）平移的方向是A－A′方向，距离是AA′的长度．（2）如下右图．问题2：如上左图．问题3：略．问题4：如图，平移△ABC，使点A移动到点A′，画出平移后的△A′B′C′．C分析：图形平移后的对应点有什么特征？作出点B和点C的对应点B′和C′，能确定△A′B′C′吗？解答：如图，连接AA′，过点B作AA′的平行线l，在l上截取BB′＝AA′，则点B′就是点B的对应点．C'类似地，你能作出点C的对应点C′，并进一步得到平移后的三角形A′B′C′吗？四、小结与作业．小结：平移特征：（1）图形形状、大小不变；（2）连接对应点连线平行且相等．作业：习题5.4．。

课题：5.4 平移【学习目标】1、了解平移的概念，会进行点的平移。

2、理解平移的性质，能解决简单的平移问题【学习重点】平移的概念和作图方法.自习自疑文【自主学习】（一）平移变换预习课本P27—P29，并完成以下练习1、观察思考：观察上面图形,我们发现他们都有一个局部和其他部分重复,如果给你一个局部,你能复制他们吗?2、探索活动：如何在一张半透明的纸上，画出一排形状和大小如图的雪人？3、思考：在所画的相邻的两个图案中，找出三组对应点，连接它们，观察它们的位置、长短有什么关系？4、平移定义：在平面内，将一个图形沿某个方向＿＿＿一定的距离，这样的图形运动称为平移，平移改变的是图形的＿＿＿＿＿。

注意：①图形的平移是由＿＿＿＿＿和＿＿＿＿＿决定的。

②平移的方向不一定水平。

5、平移性质：①平移不改变图形的＿＿＿＿和＿＿＿＿。

②经过平移所得的图形与原来的图形的对应线段＿＿＿＿＿＿＿，对应角＿＿＿＿，对应点所连的线段＿＿＿＿。

（3）如图，△DEF是由△ABC先向右平移＿＿格，再向＿＿＿平移＿＿＿格而得到的。

（4）如图，有一条小船，若把小船平移，使点A平移到点B，请你在图中画出平移后的小船。

FEDCBABAB CEDA AB COF ECB A D 自主探究文探究一如图，将梯形ABCD 的腰AB 沿AD 平移，平移长度等于AD 的长，则下列说法不正确的是（ ）A AB∥DE 且AB ＝DE B ∠DEC＝∠BC AD∥EC 且AD ＝EC D BC ＝AD ＋EC 探究二△ABC 沿BC 的方向平移到△DEF 的位置，（1）若∠B=260，∠F=740，则∠1=_______， ∠2=______，∠A=_______，∠D=______（2）若AB=4cm ，AC=5cm ，BC=4.5cm ，EC=3.5cm ，则平移的距离等于________，DF=_______，CF=_________。

探究三1、△ABC 在网格中如图所示，请根据下列提示作图 (1)向上平移2个单位长度. (2) 再向右移3个单位长度.2、已知三角形ABC 、点D ，D 为A 的对应点。

5.4平移
【学习目标】
1、了解平移的概念，会进行点的平移。

2、理解平移的性质，能解决简单的平移问题
【学习重点】平移的概念和作图方法.
【学习难点】平移的作图.
[自学]：
1、认真阅读课本：（P28-29页）
观察：
思考：在所画的相邻的两个图案中，找出三组对应点，连接它们，观察它们的位置、长短有什么关系？
2、回答什么是平移？需要几个条件？都有哪些特征？作图可以分为几步？
平移定义：
平移的性质：
平移作图步骤：
例1、应用：
问：你会把一个图形整体向某一方向移
动吗?
（1）、如图，把ΔABC整体向右移动6
格(使点A移动到点'A)，画出移动后的
三角形'A'B'C。

(请注意方格的作用)
（2）、把图中的ΔABC整体向下移动6
格 ,画出移动后的三角形A”B” C”。

(提示:一个三角形的位置显然可以由它
的三个顶点确定.)
2、认真阅读课本P29页例题，注意画图过程。

按照画图过程完成下列题目。

（1）.如图,平移线段AB,使点A 移动到点'A ,你能画出平移后的线段'A 'B 的大概位置吗?如果是使点A 移动到点"A 呢?与同学交流答案.你能从中体会平移吗?
（2）.如图,(1)平移三角形ABC,使点A 运动到A`,画出平移后的三角形A`B`C`.
A . A`
C
B
小结
1.本节课学到了什么知识？
2.还有那些收获？
课后作业：课计划19页，20页的选择填空 A
B 'A · · "A。

人教版七年级数学下册《5.4平移》教学设计PPT课件导学案教案人教版七年级数学下册《5.4平移》教学设计PPT课件导学案教案[教学目标]9. 了解平移的概念，会进行点的平移，明白得平移的性质，能解决简单的平移问题10. 培育学生的空间观念，学会用运动的观点分析问题.[教学重点与难点]重点:平移的概念和作图方式.难点:平移的作图.[教学设计]一. 观看图形形成印象生活中有许多漂亮的图案，他们都有着一起的特点，请同窗们欣赏下面图案.观看上面图形,咱们发觉他们都有一个局部和其他部份重复,若是给你一个局部,你能复制他们吗?学生试探讨论,借助举例说明.二.提出新知实践探讨平移1)把一个图形整体沿某一方向移动,会取得一个新的图形,新图形与原图形的形状和大小完全相同.(2)新图形中的每一点,都是由原图形中的某一个点移动后取得的,这两个点是对应点.(3)连接各组对应的线段平行且相等.图形的这种变换,叫做平移变换,简称平移(translation)探讨:设计一个简单的图案,利用一张半透明的纸附在上面,绘制一排形状,大小完全一样的图案三.典例剖析深化巩固例如图,(1)平移三角形ABC,使点A运动到A`,画出平移后的三角形A`B`C`.[巩固练习]教材33页:1,2,4,5,6,7[小结]1. 在平移进程中,对应点所连的线段也可能在一条直线上,当图形平移的方向是沿着一边所在直线的方向时,那么此边上的对应点必在这条直线上2. 利用平移的特点,作平行线,构造等量关系是接7题经常使用的方式.[作业]必做题:教科书33页习题:3题[备选题]1. 通过平移,三角形ABC的边AB移到了EF,作出平移后的三角形,你能给出几种作法?2. 如图,将半圆图形按箭头所指的方向平移,其中A点到了A`点,作出平移后的图形.3. 如图,在四边形ABCD中,AD//BC,AB=CD,AD<BC,AE⊥BC垂足为E,画出三角形ABE平移后的三角形,其平移方向为射线AD的方向,平移的距离为AD的长.(1) 平移后的三角形中,与B,E的对应点F,G,仍是在BC边上吗?(2) ∠B和∠C相等吗?说明理由。

云南省昆明市西山区团结民族中学七年级数学下册课题图形的平移导学案新人教版第一标设置目标【课堂目标】1.经历对图形进行观察,分析、欣赏、制作等过程，进一步发展空间观念、增强审美意识。

2.了解平移的定义，会进行简单图形的平移，理解平移的性质。

3. 认识和欣赏平移在现实生活中的应用，能运用平移进行一定的图案设计。

课堂准备：剪刀、纸、色笔、胶水、等第二标我的任务【任务1】：夯实基础（时间10分钟分值：7分）事要：一、复习欣赏优美的图案,分析图案形成过程1.观察,交流观感. 说出这是一幅什么图。

2．在平面内，将一个图形沿某个方向一定的距离，这样的图形运动称为平移，平移改变的是图形的。

平移不改变图形的和。

3．图形的平移是由和决定的。

4．经过平移所得的图形与原来的图形的对应线段，对应角，对应点所连的线段。

导框预习课本P27—P29，并完成以下练习1、观察上面图形,我们发现他们都有一个局部和其他部分重复,如果给你一个局部,你能复制他们吗?2如何在一张半透明的纸上，画出一排形状和大小如图的雪人？【任务2】：科学探究事要：1．△ABC在网格中如图所示，请根据下列提示作图(1) 向上平移2个单位长度.(2) 再向右移3个单位长度.按要求认真作图（3）与同样的方法在教科书上完成例题导框互相展示，看看谁的图美【任务3】：综合练习 事要：1．第30 页复习题1，5题能说出图形的变化过程。

2．第30 页复习题2题能说出图形的变化过程，互相展示比较评比最美创新图形。

3．第30 页复习题3，4题能说出图形的变化和平行四边形面积公式的推导过程。

导学A/B ，小组 交流讨论展示创新 第三标 反馈目标1、下列哪个图形是由左图平移得到的（ ） 2．如图所示,平移△ABC 可得到△DEF,如果∠A=50°,∠C=60°,那么∠E=•____度,∠EDF=_______度,∠F=______度,∠DOB=_______度.3．如图所示,请将图中的“蘑菇”向左平移6个格,再向下平移2个格.4．如图所示,将△ABC 平移,可以得到△DEF,点B 的对应点为点E,请画出点A 的对应点D 、点C 的对应点F 的位置. 【感悟总结】1．平移的概念和方法，你会了吗？ 2．说说生活中的平移应用。