第四章 信源编码 习题解答
- 格式:doc
- 大小:227.00 KB
- 文档页数:6


第二章部分习题2.1 试问四进制、八进制脉冲所含信息量是二进制脉冲的多少倍?答:2倍,3倍。
2.2 一副充分洗乱了的牌(含52张牌),试问 (1) 任一特定排列所给出的信息量是多少?(2) 若从中抽取13张牌,所给出的点数都不相同, 能得到多少信息量?解:(1) !52log 2 (2) 任取13张,各点数不同的概率为1352!13C ,信息量:9.4793(比特/符号)2.3 居住某地区的女孩子有%25是大学生,在女大学生中有75%是身高160厘米上的,而女孩子中身高160厘米以上的占总数的一半。
假如我们得知“身高160厘米以上的某女孩是大学生”的消息,问获得多少信息量? 答案:1.415比特/符号。
提示:设事件A 表示女大学生,事件C 表示160CM 以上的女孩,则问题就是求p(A|C),83214341)()|()()()()|(=⨯===C p A C p A p C p AC p C A p2.4 设离散无忆信源()123401233/81/41/41/8X a a a a P X ====⎛⎫⎧⎫=⎨⎬ ⎪⎩⎭⎝⎭,其发出的消息为(2021201302130012032101103210100223210),求(1) 此消息的自信息量是多少?(2) 在此消息中平均每个符号携带的信息量是多少?解:(1)87.81比特,(2)1.951比特。
提示:先计算此消息出现的概率,再用自信息量除以此消息包含的符号总数(共45个)。
2.5 从大量统计资料知道,男性中红绿色盲的发病率为7% ,女性发病率为0.5%,如果你问一位男士:“你是否是色盲?”他的回答可能是“是”,可能是“否”,问这两个回答中各含有多少信息量?平均每个回答中含有多少信息量?如果问一位女士,则答案中含有的平均自信息量是多少?(1) 男性回答是的信息量为2log 0.07 3.8369-=比特,回答否的信息量是0.1047比特,平均每个回答含的信息量(即熵)是0.36596比特。



第4章习题4-1 对信源⎥⎦⎤⎢⎣⎡=⎥⎦⎤⎢⎣⎡01.010.015.017.018.019.02.0s s s s s s s P S 7654321进行二元编码,编码方案为(1)计算平均码长L ; (2)编码后信息传输率R ;(3)编码信息率R '; (4)编码效率η。
解:(1)()14.3Ls p L iq1i i=⋅=∑=(码元/信源符号)(2)()61.2S H =(比特/信源符号)()831.014.361.2L S ===H R (bit/码元) (3)logr L R ='=3.14( bit/信源符号) (4)831.0R Rmax==η 或者()831.0R S H ='=η 4-2 设离散无记忆信源的概率空间为⎥⎥⎦⎤⎢⎢⎣⎡=⎥⎦⎤⎢⎣⎡4143s s S 21P ,若对信源采取等长二元编码,要求编码效率96.0=η,允许译码错误概率510-≤δ,试计算需要的信源序列长度N 为多少?解:信源熵为()811034log 434log 41S .Η=+=(bit/符号)自信息量的方差()()()[]22i q1i i 2S H logp p S -=∑=σ4715.0811.041log 4143log 43222=-⎪⎭⎫⎝⎛+⎪⎭⎫ ⎝⎛= 因为编码效率96.0=η,由()()ε+=S S H H η可得()3379.0811.096.004.0S H 1=⨯=-=ηηε 可得()752221013.4103379.04715.0S N ⨯=⨯=≥-δεσ 所以,信源序列长度达到71013.4⨯以上,才能实现给定的要求,因此等长编码没有实际的意义,一般统计编码都是采用不等长编码。
4-6设离散无记忆信源的概率空间为⎥⎦⎤⎢⎣⎡=⎥⎦⎤⎢⎣⎡1.09.0s s S 21P ,对信源进行N 次扩展,采用霍夫曼编码。
当N=1,2,∞时的平均码长和编码效率为多少?解:(1)N=1时,将1s 编成0,2s 编成1,则1L 1=又因为信源熵()469.0))logp(s p(s S H q1i i i =-=∑=bit/符号所以()469.0L S H 11==η (2)N=2时,编码过程如下2S概率 霍夫曼编码11s s 0.81121s s 0.09 01 12s s 0.09 000 22s s 0.01001所以()=+⨯+⨯+⨯=0.090.0130.0920.811L 2则645.02L 2= 所以()==0.645X H 2η (3)N=∞时,由香农第一定理可知,必然存在唯一可译码,使()S H N L limr NN =∞→而霍夫曼编码为最佳码,即平均码长最短的码,故()()469.0S H S H N L limr NN ===∞→即1lim N N =∞→η4-7已知信源共7个符号消息,其概率空间为()⎥⎦⎤⎢⎣⎡=⎥⎦⎤⎢⎣⎡01.010.015.017.018.019.02.0s s s s s s s x P S 7654321试进行香农编码。
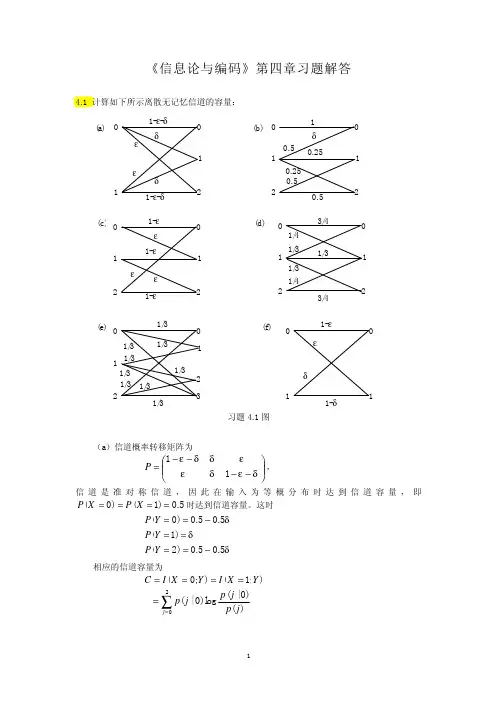

4-1 设有一个二元等该率信源{}1,0∈X ,2/110==p p ,通过一个二进制对称信道(BSC )。
其失真函数ij d 与信道转移概率ij p 分别定义为 j i j i d ij =≠⎩⎨⎧=,0,1 ,j i ji p ij =≠⎩⎨⎧-=,1,εε试求失真矩阵d 和平均失真D 。
解:由题意得,失真矩阵为d ⎥⎦⎤⎢⎣⎡=0110d ,信道转移概率矩阵为P ⎥⎦⎤⎢⎣⎡--=εεεε11)(i j 平均失真为εεεεε=⨯-+⨯+⨯+⨯-==∑0)1(211211210)1(21),()()(,j i d i j p i p D ji 4-3 设输入符号与输出符号X 和Y 均取值于{0,1,2,3},且输入符号的概率分布为P(X=i)=1/4,i=0,1,2,3,设失真矩阵为⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡=0111101111011110d 求)(),(,,max min max min D R D R D D 以及相应的编码器转移概率矩阵。
解:由题意,得 0min =D则symbol bit X H R D R /24log )()0()(2min ====这时信源无失真,0→0,1→1,2→2,3→3,相应的编码器转移概率矩阵为⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡=1000010000100001)j (i P ∑===33,2,1,0max ),()(min i j j i d i p D,,141141041141141141141041min{⨯+⨯+⨯+⨯⨯+⨯+⨯+⨯=}041141141141141041141141⨯+⨯+⨯+⨯⨯+⨯+⨯+⨯, 43}43,43,43,43min{==则0)(max =D R此时输出概率分布可有多种,其中一种为:p(0)=1,p(1)=p(2)=p(3)=0则相应的编码器转移概率矩阵为⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡=0001000100010001)(i j P4-5 具有符号集{}10,u u U =的二元信源,信源发生概率为:2/10,1)(,)(10≤<-==p p u p p u p 。

第四章信源编码习题解答1种编码方法:1)哪些是非奇异码哪些是唯一可译码哪些是即时码2)分别计算每个唯一可译码的平均码长和编码效率。
解:1)A、B、C、D、E、F是非奇异码。
A、B、C、F是唯一可译码(E不满足克拉夫特不等式)。
A、C、F是即时码(B是续长码)。
3)编码A:平均码长:3AL=码元/消息信源熵:111111()lb lb4lb222441616H X=---⨯=比特/消息编码效率:max ()/2/366.7% lb21AH H X L Hη====码码编码B和C:平均码长:11111123456 2.1252416161616B CL L==+⨯+⨯+⨯+⨯+⨯=码元/消息编码效率:max ()/2/2.12594.1% lb21B CH H X L Hηη=====码码编码F:平均码长:111234 2.52416FL⎛⎫=⨯+⨯+⨯=⎪⎝⎭码元/消息编码效率:max ()/2/2.580%lb21F H H X L H η====码码2、离散无记忆信源X 的概率空间为:1234567()0.200.190.180.170.150.100.01X x x x x x x x p X ⎧⎫⎡⎤=⎨⎬⎢⎥⎩⎭⎣⎦ 1)对其进行费诺编码,并计算其编码效率;2)对其进行哈夫曼编码,并将其编码效率与费诺编码相比较。
解:1平均码长:()()()0.20.1720.190.180.1530.10.014 2.74L =+⨯+++⨯++⨯=码元/符号 信源熵:()0.20lb0.200.19lb0.190.18lb0.180.17lb0.170.15lb0.150.1lb0.10.01lb0.01 2.60/874H X =-------= 比特符号编码后平均码元熵:() 2.608740.95212.74H X H L===码比特/码元编码效率:max 0.952195.21%lb2H H η===码码2)哈夫曼编码: 码长码字 信源X (X )2 10 x 1 2 11 x 2 3000 x 33 001 x 43 010 x 54 0110 x 64 0111x 7平均码长:()()()0.20.1920.180.170.1530.10.014 2.72L =+⨯+++⨯++⨯=码元/符号 编码后平均码元熵:() 2.608740.95912.72H X H L===码比特/码元编码效率:max 0.959195.91%lb2H H η===码码与费诺编码相比,哈夫曼编码的编码效率要高于费诺编码。

第一章:信源编码的概念(绪论)1. 数据压缩的一个基本问题是“我们要压缩什么?”;你对此如何理解?2. 你所了解的各类编码的目的是什么?请各举一例解释编码作用。
3. 你怎样理解信息率失真函数R (D )对于信源编码的指导作用?试举例。
4. 等概率信源还能否压缩?为什么?请举例说明。
5 你理解的联合编码的发展方向是什么?信源编码的发展趋势和进展有哪些?第二章:无损信源编码1.有二元独立序列,已知00.9p =,10.1p =,求这序列的符号熵。
当用赫夫曼编码时,以三个二元符号合成一个新符号,求这种符号的平均代码长度和编码效率。
设输入二元符号的速率是每秒100个,要求三分钟内溢出和取空的概率均小于0.01,求所需要的信道码率(bit/s )和存储器容量(比特数)。
若信道码率已规定为50 bit/s ,存储器容量将如何选择?2.有二元平稳马氏链,已知P (0|0)=0.8,P (1|1)=0.7,求它的符号熵。
用三个符号合成一个来编赫夫曼码,求这新符号的平均代码长度和编码效率。
3.对上题的信源进行游程编码。
若“0”游程长度的截止值是16,“1”游程的截止值是8,求编码效率。
这样的编码效率是否已达到最佳?为什么?4.求三阶马氏链的“0”游程长度和“1”游程长度的条件概率,设原序列的条件概率为:P (0|r )=r a其中r=0,1,2,···7,是前三位的二进制位数。
5.计算帧长N=63,信息位数Q=0,1,2,4,8,16,和32时L-D 码和信息标志码的压缩率,并讨论计算结果。
第三章:算术编码1.已知二元序列的概率011/8,7/8p p ==011/8,7/8p p ==。
试对下列序列编算数码,取W=3的计算精度,并计算符号的平均码长:11111111110111111111102.计算上题的序列的符号熵,并与算数码的符号平均码长比较,理解这一结果。
3.已知二元平稳马氏链的条件概率为p (0|0)=1/2,p (0|1)=1/4;用最低精度位数对下列序列编算数码,并计算符号的平均码长:111101011110010111100000111111114.若对上题序列以二位并元处理来编赫夫曼码,则符号的平均码长是多少?并与上题的结果比较。


信息论与编码理论-第4章无失真信源编码-习题解答-20071202信息论与编码理论第4章无失真信源编码习题及其参考答案4-1 有一信源,它有六个可能的输出,其概率分布如下表所示,表中给出了对应的码A、B、C、D、E和F(1)求这些码中哪些是唯一可译码;(2)求哪些码是及时码;(3)对所有唯一可译码求出其平均码长。
?X??s14-2 设信源????p(s)P(X)???1s6?p(s2)?p(s6)???s2?p(s)?1。
对此次能源进行m元唯一ii?16可译编码,其对应的码长为(l1,l2,…,l6)=(1,1,2,3,2,3),求m值的最好下限。
(提示:用kraft不等式)?s?X??14-3设信源为??1??p(X)???2?(1)信源的符号熵;(2)这种码的编码效率;s214s3s411816s5132s6s7s8?,编成这样的码:(000,001,111???64128128?010,011,100,101,110,111)。
求(3)相应的仙农码和费诺码。
4-4求概率分布为(,11122信)源的二元霍夫曼编码。
讨论此码对于概率分布为355151511111(,,,,)的信源也是最佳二元码。
555554-5有两个信源X和Y如下:1信息论与编码理论s2s3s4s5s6s7??X??s1??p(X)??0.200.190.180.170.150.100.01?????s2s3s4s5s6s7s8s9??Y??s1??p(Y)??0.490.140.140.070.070.040.020.02 0.01?????(1)用二元霍夫曼编码、仙农编码以及费诺编码对信源X和Y进行编码,并计算其平均码长和编码效率;(2)从X,Y两种不同信源来比较三种编码方法的优缺点。
4-6设二元霍夫曼码为(00,01,10,11)和(0,10,110,111),求出可以编得这样霍夫曼码的信源的所有概率分布。
4-7设信源为?码。
4.5若将N 个相同的BSC 级联如题图4.5所示,各信道的转移概率矩阵为⎥⎦⎤⎢⎣⎡--p p p p 11。
令Q t =P{X t =0},t=0,1,…,N,且Q 0为已知。
题图 4.5(a)求Q t 的表达式。
(b)证明N →∞时有Q N →1/2,且与Q 0取值无关,从而证明N →∞级联信道的信道容量C N →0,P>0。
解:(a)对于满足X N 为马氏链的串联信道,他们总的信道转移概率矩阵为各个串联信道矩阵的乘积,即P(X N |X 0)= P(X 1|X 0) P(X 2|X 1)……P(X N |X N-1)由已知得,但各信道的转移概率矩阵为⎥⎦⎤⎢⎣⎡--p p p p 11 则两个信道级联的转移概率矩阵为: P 2=⎥⎦⎤⎢⎣⎡--p p p p 11⎥⎦⎤⎢⎣⎡--p p p p 11=()()()()⎥⎦⎤⎢⎣⎡-+---+2222112p 12p 1p p p p p p 三个信道级联的转移概率矩阵为: P 3=()()()()⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡-+----+33331221211221211221211-2p 2121p p p 四个信道级联的转移概率矩阵为: P 4=()()()()⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡-+----+44441221211221211221211-2p 2121p p p 以此类推:可得N 个信道级联的转移概率矩阵为:P N =()()()()⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡-+----+N N N N p p p 1221211221211221211-2p 2121 则Q t =P{X t =0}=()()()()()000121221211122121122121Q p p Q p Q p t t t t -+--=-⎥⎦⎤⎢⎣⎡--+⎥⎦⎤⎢⎣⎡-+即Q t 的表达式为:Q t =()()012122121Q p p t t -+-- t=0,1,……,N (b) 由(a)可得到:Q N =()()012122121Q p p t t -+-- 由0<p<1,则0<2p<2,-1<2p-1<1,即|2p-1|<1 则21lim =∞→N N Q ,与Q 0取值无关。
第4章无失真信源编码习题及其参考答案4-1 有一信源,它有六个可能的输出,其概率分布如下表所示,表中给出了对应的码A、B、C、D、E和F(1)求这些码中哪些是唯一可译码;(2)求哪些码是及时码;(3)对所有唯一可译码求出其平均码长l。
4-2 设信源61261126()1()()()()iis s sXp sp s p s p sP X=⎡⎤⎡⎤==⎢⎥⎢⎥⎣⎦⎣⎦∑。
对此次能源进行m元唯一可译编码,其对应的码长为(l1,l2,…,l6)=(1,1,2,3,2,3),求m值的最好下限。
(提示:用kraft不等式)4-3设信源为1234567811111111()248163264128128s s s s s s s sXp X⎡⎤⎡⎤⎢⎥=⎢⎥⎢⎥⎣⎦⎢⎥⎣⎦,编成这样的码:(000,001,010,011,100,101,110,111)。
求(1)信源的符号熵;(2)这种码的编码效率;(3)相应的仙农码和费诺码。
4-4求概率分布为11122(,,,,)3551515信源的二元霍夫曼编码。
讨论此码对于概率分布为11111(,,,,)55555的信源也是最佳二元码。
4-5有两个信源X和Y如下:121234567()0.200.190.180.170.150.100.01X s s s s s s s p X ⎡⎤⎡⎤=⎢⎥⎢⎥⎣⎦⎣⎦123456789()0.490.140.140.070.070.040.020.020.01Y s s s s s s s s s p Y ⎡⎤⎡⎤=⎢⎥⎢⎥⎣⎦⎣⎦(1)用二元霍夫曼编码、仙农编码以及费诺编码对信源X 和Y 进行编码,并计算其平均码长和编码效率;(2)从X ,Y 两种不同信源来比较三种编码方法的优缺点。
4-6设二元霍夫曼码为(00,01,10,11)和(0,10,110,111),求出可以编得这样 霍夫曼码的信源的所有概率分布。
4-7设信源为12345678()0.40.20.10.10.050.050.050.05X s s s s s s s s p X ⎡⎤⎡⎤=⎢⎥⎢⎥⎣⎦⎣⎦,求其三元霍夫曼编码。