下载文档原格式
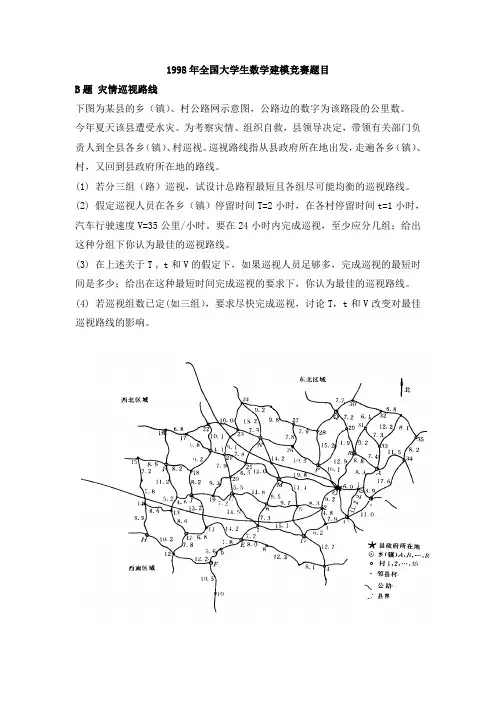
1998年全国大学生数学建模竞赛题目B题灾情巡视路线下图为某县的乡（镇）、村公路网示意图，公路边的数字为该路段的公里数。
今年夏天该县遭受水灾。
为考察灾情、组织自救，县领导决定，带领有关部门负责人到全县各乡（镇）、村巡视。
巡视路线指从县政府所在地出发，走遍各乡（镇）、村，又回到县政府所在地的路线。
(1) 若分三组（路）巡视，试设计总路程最短且各组尽可能均衡的巡视路线。
(2) 假定巡视人员在各乡（镇）停留时间T=2小时，在各村停留时间t=1小时，汽车行驶速度V=35公里/小时。
要在24小时内完成巡视，至少应分几组；给出这种分组下你认为最佳的巡视路线。
(3) 在上述关于T , t和V的假定下，如果巡视人员足够多，完成巡视的最短时间是多少；给出在这种最短时间完成巡视的要求下，你认为最佳的巡视路线。
(4) 若巡视组数已定(如三组），要求尽快完成巡视，讨论T，t和V改变对最佳巡视路线的影响。
灾情巡视路线模型摘要本文将求最佳巡视路线间题转化为图论中求最佳推销员回路（哈米尔顿回路）的问题,并用近似算法去寻求近似最优解。
对赋权图中的路径分组问题定义了均衡度用以衡量分组的均衡性。
对问题1和问题2先定出几个分的准则进行初步分组,并用近似算法求每一组的近似最佳推销员回路,再根据均衡度进行微调,得到较优的均衡分组和每组的近似最佳推销员回路。
对问题1，运用求任意两点间最短路的Floyd算法,得出总路程较短且各组尽可能均衡的路线,各组的巡视路程分别为216.4公里,191.1公里,192.3公里,总路程599.8公里。
对问题2,证明了应至少分为4组,并求出了分为4组时各组的较优巡视路线,各组的巡视时间分别为22.74小时,22.59小时,21.69小时,22.54小时。
对问题3,求出完成巡视的最短时间为6.43小时,并用较为合理的分组的准则,分成22个组对问题4，研究了在不影响分组的均衡条件下, T,t,V的允许变化范围,并得出了这三个变量的关系式,并由此对分三个组的情况进行了具体讨论。
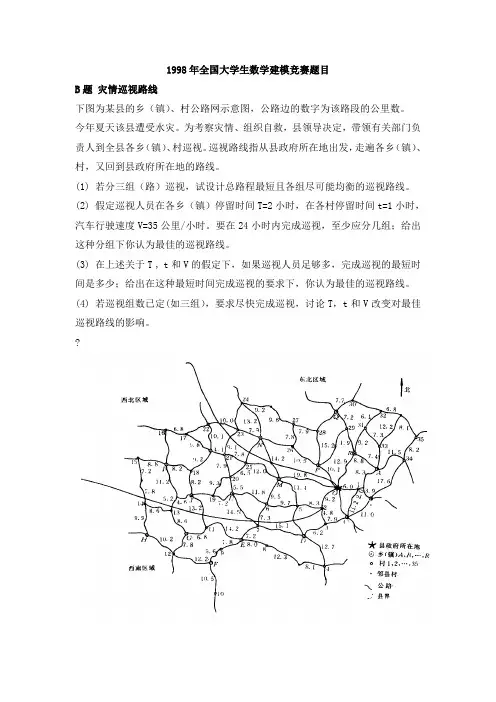
1998年全国大学生数学建模竞赛题目B题灾情巡视路线下图为某县的乡（镇）、村公路网示意图，公路边的数字为该路段的公里数。
今年夏天该县遭受水灾。
为考察灾情、组织自救，县领导决定，带领有关部门负责人到全县各乡（镇）、村巡视。
巡视路线指从县政府所在地出发，走遍各乡（镇）、村，又回到县政府所在地的路线。
(1) 若分三组（路）巡视，试设计总路程最短且各组尽可能均衡的巡视路线。
(2) 假定巡视人员在各乡（镇）停留时间T=2小时，在各村停留时间t=1小时，汽车行驶速度V=35公里/小时。
要在24小时内完成巡视，至少应分几组；给出这种分组下你认为最佳的巡视路线。
(3) 在上述关于T , t和V的假定下，如果巡视人员足够多，完成巡视的最短时间是多少；给出在这种最短时间完成巡视的要求下，你认为最佳的巡视路线。
(4) 若巡视组数已定(如三组），要求尽快完成巡视，讨论T，t和V改变对最佳巡视路线的影响。
?灾情巡视路线模型摘要本文将求最佳巡视路线间题转化为图论中求最佳推销员回路（哈米尔顿回路）的问题,并用近似算法去寻求近似最优解。
对赋权图中的路径分组问题定义了均衡度用以衡量分组的均衡性。
对问题1和问题2先定出几个分的准则进行初步分组,并用近似算法求每一组的近似最佳推销员回路,再根据均衡度进行微调,得到较优的均衡分组和每组的近似最佳推销员回路。
对问题1，运用求任意两点间最短路的Floyd算法,得出总路程较短且各组尽可能均衡的路线,各组的巡视路程分别为公里,公里,公里,总路程公里。
对问题2,证明了应至少分为4组,并求出了分为4组时各组的较优巡视路线,各组的巡视时间分别为小时,小时,小时,小时。
对问题3,求出完成巡视的最短时间为小时,并用较为合理的分组的准则,分成22个组对问题4，研究了在不影响分组的均衡条件下, T,t,V的允许变化范围,并得出了这三个变量的关系式,并由此对分三个组的情况进行了具体讨论。
关键词：最佳推销员回路问题哈米尔顿回路赋权图近似算法均衡度一、问题重述1998年夏天某县遭受水灾。
题目：灾情巡视路线学号：2012070231姓名：施亚男班级：12级数学教育一．问题重述1.1背景分析：今年夏天该县遭受水灾。
为考察灾情、组织自救，县领导决定，带领有关部门负责人到全县各乡（镇）、村巡视。
巡视路线指从县政府所在地出发，走遍各乡（镇）、村，又回到县政府所在地的路线。
1.2需要解决的问题：1）若分三组（路）巡视，试设计总路程最短且各组尽可能均衡的巡视路线。
2）假定巡视人员在各乡（镇）停留时间T=2小时，在各村停留时间t=1小时，汽车行驶速度V=35公里/小时。
要在24小时内完成巡视，至少应分几组；给出这种分组下你认为最佳的巡视路线。
3）在上述关于T , t和V的假定下，如果巡视人员足够多，完成巡视的最短时间是多少；给出在这种最短时间完成巡视的要求下，你认为最佳的巡视路线。
4）若巡视组数已定(如三组），要求尽快完成巡视，讨论T，t和V改变对最佳巡视路线的影响。
一、模型假设2.1假设地面情况一切正常，不会影响汽车行驶速度；2.2假设第二次经过的乡镇，不计算停留时间；2.3对于同一乡镇，如果某一小组停留过，其他小组经过时不计算停留时间；2.4假设经过邻县村不做任何停留；2.5假设县镇府所在地灾情不派小组人员巡视。
二、符号说明三、 问题分析本文研究的是考察灾情最佳巡视线路设计的问题，准确合理的路线设计对灾情巡视救治起着重要作用。
为很好的解决此问题，为此我们建立了网络图模型。
对于问题一，题目要求在分三组巡视的情况下，使总路程最短且各小组所走路程均衡。
先考虑分区，我们将得出的最小生成树图形和最短路树图形，进行比较并找出其公共部分。
分组要求尽量不破坏最短生成树和最小生成树，所以我们以公共部分为界限，将此网络图分为三组。
为使每小组所走路程均衡，我们引入了均衡度α。
它表示最大路程和最小路程的差值与最大路程的比值。
α越小，表示均衡度越好。
以总路程最短和均衡度最小作为目标函数建立多目标规划模型，利用哈密顿原理得出各组的巡回路线，并对其分析修正求得各组最优巡回路线。
最佳灾情巡视路线模型【摘要】“图论”是组合数学的分支，它与其他的数学分支，如群论、矩阵论、拓扑学，数值分析有着密切的联系。
在其它科学领域，如计算机科学、运筹学、电网络分析、化学物理以及社会科学等方面图论也具有越来越重要的地位，并已取得丰硕的成果。
而且，图论的理论和方法在数学建模中也有重要应用。
本文概述了一些常用的图论方法和算法，并通过举例（灾情巡视路线）说明其在数学建模中的应用。
【关键词】图论灾情巡视Hamilton回路数学模型预备知识定义1 完全图：如果图G中每一对不同的顶点恰有一条边连接，则称此图为完全图。
定义2 连通图：如果对图G=（V，E）的任何两个顶点u与v，G中存在一条（u-v）路。
则称G是连通图。
定义3 加权图：边上有数的图称为加权图。
在加权图中，链（迹、路）的长度为链（迹、路）上的所有边的权植的和。
定义4 Hamilton回路：图G中的一个回路C称为一个Hamilton回路如果C含有G 的所有顶点。
含有Hamilton回路的图称为Hamilton图。
定义5 欧拉回路：经过图G的每条边的迹称为欧拉迹，如果这条迹是闭的，则称这条闭迹为G的欧拉回路。
一数学建模中常用的图论方法1 迪克斯特拉算法（Dijkstra）1.1问题来源在加权图中，我们经常需要找出两个指定点之间的最短路，通常称为最短路问题。
解决最短路问题的方法之一就是迪克斯特拉算法。
1.2基本思路假定P：V1→V2→ (V)i→…→Vj→…→Vk是从V1到Vk的最短路，则它的子路Vi →…→Vj一定是从Vi到Vj的最短路。
否则从V1出发沿路p走到Vi，,然后沿Vi 到Vj的最短路走到Vj再沿路P从Vj到Vk，这样得到一条新的从V1出发到Vk的路，其长度小于P，与P是最短路的假设矛盾。
1.3算法设G为所有权都为正数的加权连通简单图。
G带有顶点a=V0, V1, (V)n=z,权W(Vi , Vj) ,若(Vi, Vj)不是G中的边，则W(Vi, Vj) =∞for i=1 to nL((Vi)= ∞L(a)=0S=Ф(初始化标记，a的标记为0，其它结点标记为∞，S 为空集)当z不属于S时beginu=不属于S的L（u）最小的一个顶点S=S∪{u}对所有不属于S的顶点Vif L(u)+W(u,v)<L(v) thenL(v)=L(u)+L(u,v) (这样就给S中添加带最小标记的顶点并且更新不在S中的顶点的标记)End (L(z)表示从a到z的最短路的长度) 这个算法经过n-1次循环后必定结束，计算量为1/2（n-1）(n-2)，因而是个有效算法。
非线性仿真技术在零件结构大变形设计中的应用摘要：通过零件本身变形来实现零件之间的连接在产品设计中使用非常普遍广泛，变形的关键在于材料特性，零件本身结构及使其变形的约束条件。
本文利用NX 高级仿真中的[SOL601,106 Advanced Nonlinear Statics]结构非线性静态分析模块，对零件受力发生塑性变形进行仿真分析，对零件结构和设计参数进行了改进，并为确定合理的压接工艺提供依据。
关键词：非线性仿真，SOL601,106，塑性变形引文：通过零件自身的变形产生装配连接的方式，在实际的结构装配中广泛使用，由于无需添加额外装配件，只需要在装配时使其发生塑性变形或弹性变形产生挂台，便可以实现连接，例如常见的塑料件卡扣连接等，不仅节省了物料，同时也大大降低了物流和装配费用，成本低廉。
特别是在结构安装的空间和方向上受限的时候，由于结构简洁便于控制，优势尤为明显。
连接器设计的关键问题在于材料的选择，变形结构的设计及工艺的确定。
引入仿真之前，这些验证需要投入多种的试验，实验设备，物料准备和试验时间大大限制了产品设计时间。
本文以实际工作中采用仿真方法来替代实验验证，并对设计做出优化，得到了满意的效果。
正文：案例所示的金属连接器，结构如图1a所示，压接变形为图1b，理论设计的最大位移为2mm，在外力作用下，连接器的应力超过材料的屈服极限而未到强度极限，此时的零件发生塑性变形，产生挂台，从而起到连接的作用。
图1a 图1b在此过程中，材料发生了塑性变形，几何形状发生了大变形，新的接触面也产生，属于非线性大位移大变形问题。
对此问题的仿真，本文采用了NX 高级仿真中的[SOL601,106 Advanced Nonlinear Statics]结构非线性静态分析模块，主要解决的问题是校验设计合理性，确定生产工艺。
整个验证过程一共进行了三组仿真，一是连接器变形导向的仿真，包括形状及公差；二是压接工艺的设计仿真；三是校核整个零件变形后的几何形状。
1998年全国大学生数学建模竞赛题目B题灾情巡视路线下图为某县的乡（镇）、村公路网示意图，公路边的数字为该路段的公里数。
今年夏天该县遭受水灾。
为考察灾情、组织自救，县领导决定，带领有关部门负责人到全县各乡（镇）、村巡视。
巡视路线指从县政府所在地出发，走遍各乡（镇）、村，又回到县政府所在地的路线。
(1) 若分三组（路）巡视，试设计总路程最短且各组尽可能均衡的巡视路线。
(2) 假定巡视人员在各乡（镇）停留时间T=2小时，在各村停留时间t=1小时，汽车行驶速度V=35公里/小时。
要在24小时内完成巡视，至少应分几组；给出这种分组下你认为最佳的巡视路线。
(3) 在上述关于T , t和V的假定下，如果巡视人员足够多，完成巡视的最短时间是多少；给出在这种最短时间完成巡视的要求下，你认为最佳的巡视路线。
(4) 若巡视组数已定(如三组），要求尽快完成巡视，讨论T，t和V改变对最佳巡视路线的影响。
灾情巡视路线模型摘要本文将求最佳巡视路线间题转化为图论中求最佳推销员回路（哈米尔顿回路）的问题,并用近似算法去寻求近似最优解。
对赋权图中的路径分组问题定义了均衡度用以衡量分组的均衡性。
对问题1和问题2先定出几个分的准则进行初步分组,并用近似算法求每一组的近似最佳推销员回路,再根据均衡度进行微调,得到较优的均衡分组和每组的近似最佳推销员回路。
对问题1，运用求任意两点间最短路的Floyd算法,得出总路程较短且各组尽可能均衡的路线,各组的巡视路程分别为216.4公里,191.1公里,192.3公里,总路程599.8公里。
对问题2,证明了应至少分为4组,并求出了分为4组时各组的较优巡视路线,各组的巡视时间分别为22.74小时,22.59小时,21.69小时,22.54小时。
对问题3,求出完成巡视的最短时间为6.43小时,并用较为合理的分组的准则,分成22个组对问题4，研究了在不影响分组的均衡条件下, T,t,V的允许变化范围,并得出了这三个变量的关系式,并由此对分三个组的情况进行了具体讨论。
1998年全国大学生数学建模竞赛题目创作：欧阳科B题灾情巡视路线下图为某县的乡（镇）、村公路网示意图，公路边的数字为该路段的公里数。
今年夏天该县遭受水灾。
为考察灾情、组织自救，县领导决定，带领有关部门负责人到全县各乡（镇）、村巡视。
巡视路线指从县政府所在地出发，走遍各乡（镇）、村, 又回到县政府所在地的路线。
（1）若分三组（路）巡视，试设计总路程最短且各组尽可能均衡的巡视路线。
⑵ 假定巡视人员在各乡（镇）停留时间T二2小时，在各村停留时间t=l小时，汽车行驶速度V二35公里/小时。
要在24小时内完成巡视，至少应分几组；给出这种分组下你认为最佳的巡视路线。
（3）在上述关于T ,上和^的假定下，如果巡视人员足够多，完成巡视的最短时间是多少；给出在这种最短时间完成巡视的要求下，你认为最佳的巡视路线。
（4）若巡视组数已定（如三组），要求尽快完成巡视，讨论T, t和V改变对最佳巡视路线的影响。
灾情巡视路线模型摘要本文将求最佳巡视路线间题转化为图论中求最佳推销员回路（哈米尔顿回路）的问题，并用近似算法去寻求近似最优解。
对赋权图中的路径分组问题定义了均衡度用以衡量分组的均衡性。
对问题1和问题2先定出几个分的准则进行初步分组，并用近似算法求每一组的近似最佳推销员回路，再根据均衡度进行微调，得到较优的均衡分组和每组的近似最佳推销员回路。
对问题1,运用求任意两点间最短路的Floyd算法,得出总路程较短且各组尽可能均衡的路线，各组的巡视路程分别为216.4公里,191.1公里,192.3公里,总路程599.8公里。
对问题2,证明了应至少分为4组,并求出了分为4组时各组的较优巡视路线，各组的巡视时间分别为22.74小时,22.59小时,21.69小时,22.54小时。
对问题3,求出完成巡视的最短时间为6.43小时,并用较为合理的分组的准则，分成22个组对问题4,研究了在不影响分组的均衡条件下,T,t,V 的允许变化范围，并得出了这三个变量的关系式，并由此对分三个组的情况进行了具体讨论。
灾难最佳巡视路线摘要本文解决的是对全县的乡镇和村庄进行灾情巡视最佳线路的求解问题，多旅行售货问题。
问题一是三个旅行售货问题，问题二是四个旅行售货问题。
我们可以运用图论的知识并且考虑气均衡性，建立起约束最优化线路模型来解决这个问题。
关键词：Hamilton圈多旅行售货问题最小生成树问题今年夏天该县遭受水灾。
为考察灾情、组织自救，县领导决定，带领有关部门负责人到全县各乡（镇）、村巡视。
巡视路线指从县政府所在地出发，走遍各乡（镇）、村，又回到县政府所在地的路线。
1.若分三组（路）巡视，试设计总路程最短且各组尽可能均衡的巡视路线。
2.假定巡视人员在各乡（镇）停留时间T=2小时，在各村停留时间t=1小时，汽车行驶速度V=35公里/小时。
要在24小时内完成巡视，至少应分几组；给出这种分组下你认为最佳的巡视路线。
1.问题重述问题1：若分三组（路）巡视，试设计总路程最短且各组尽可能均衡的巡视路线图问题2：假定巡视人员在各乡（镇）停留时间T=2小时，在各村停留时间t=1小时，汽车行驶速度V=35公里/小时。
要在24小时内完成巡视，至少应分几组；给出这种分组下你认为最佳的巡视路线。
问题3：在上述关于T , t和V的假定下，如果巡视人员足够多，完成巡视的最短时间是多少；给出在这种最短时间完成巡视的要求下，你认为最佳的巡视路线。
问题4：若巡视组数已定(如三组），要求尽快完成巡视，讨论T，t和V改变对最佳巡视路线的影响。
2.模型的假设及符号说明2.1模型假设假设1：假设汽车在路上以V匀速行驶，且不停留，不考虑故障，忽略外部因素影响假设2：巡视过程中除了正常停留外，没有因其它因素造成时间延误假设3：巡视路线可以重复假设4：对于要多次经过的乡(镇)或村只停留一次假设5：每个巡视人员只能走自己划分区域内的路线2.2符号说明G：表示加权图Gi：表示子图V：表示顶点，每一个乡(镇)或村看成一个点E：表示边，乡(镇)或村之间的路线w(x，y)：表示权重，乡(镇)或村之间的距离S：表示回路路程总和ə：表示路程均衡度Li：表示每一条子回路T：表示在每个乡(镇)停留的时间I：表示在每个村停留的时间Ti：表示第i组的巡视时间V：表示汽车行驶速度Z：表示划分的区域数N：表示乡(镇)的数目N：表示村的数目Ni：表示第i组巡视乡(镇)的数目Ni：表示第i组巡视村的数目M：表示所分的组数v ：表示时间均衡度3.问题分析本文研究的是最佳巡视路线设计问题，要求从O点出发巡视完所有乡(镇)村后，在回到O点，此问题可以转化为旅行商问题，再设计相应的算法求解针对问题一：问题一要求设计3组巡视总路程最短且尽可能均衡，首先我们通过主观筛选法将原图划分为3个子图，每个子图顶点数大约为17个，相邻的点划在一个子图中，且尽量使每个子图构成一个回路，这样将原问题转化为单旅行商问题求解针对问题二：问题二在问题一的基础上加了时间的限制，在每一个顶点都有停留时间，且在24小时巡视完。
建模案例：最佳灾情巡视路线
1998年全国大学生数学模型竞赛B题中的两个问题.
一、问题
今年夏天某县遭受水灾.为考察灾情、组织自救，县领导决定，带领有关部门负责人到全县各乡（镇）、村巡视.巡视路线指从县政府所在地出发，走遍各乡（镇）、村，又回到县政府所在地的路线.
1．若分三组（路）巡视，试设计总路程最短且各组尽可能均衡的路线.
2．假定巡视人员在各乡（镇）停留时间T=2h，在各村停留时间t=1h，汽车行驶速度V=35km/h.要在24h内完成巡视，至少应分几组；给出这种分组下最佳的巡视路线.
乡镇、村的公路网示意图见图1.
图1
二、假设
1．汽车在路上的速度总是一定，不会出现抛锚等现象；
2．巡视当中，在每个乡镇、村的停留时间一定，不会出现特殊情况而延误时间；3．每个小组的汽车行驶速度完全一样；
4．分组后，各小组只能走自己区内的路，不能走其他小组的路（除公共路外）.
三、模型的建立与求解
将公路网图中，每个乡（镇）或村看作图中的一个节点，各乡（镇）、村之间的公路看作图中对应节点间的边，各条公路的长度（或行驶时间）看作对应边
上的权，所给公路网就转化为加权网络图，问题就转化为在给定的加权网络图中寻找从给定点O 出发，行遍所有顶点至少一次再回到O 点，使得总权（路程或时间）最小，此即最佳推销员回路问题.
在加权图G 中求最佳推销员回路问题是NP —完全问题，我们采用一种近似算法求出该问题的一个近似最优解，来代替最优解，算法如下：
算法一 求加权图G （V ，E ）的最佳推销员回路的近似算法：
1． 用图论软件包求出G 中任意两个顶点间的最短路，构造出完备图
),(E V G ''，()E y x '∈∀,， ()(),,G x y mind x y ω=；
2． 输入图G '的一个初始H 圈；
3． 用对角线完全算法产生一个初始H 圈；
4． 随机搜索出G '中若干个H 圈，例如2000个；
5． 对第2、3、4步所得的每个H 圈，用二边逐次修正法进行优化，得到近似最佳H 圈；
6． 在第5步求出的所有H 圈中，找出权最小的一个，此即要找的最佳H 圈的近似解.
由于二边逐次修正法的结果与初始圈有关，故本算法第2、3、4步分别用三种方法产生初始圈，以保证能得到较优的计算结果.
问题一 若分为3组巡视，设计总路程最短且各组尽可能均衡的巡视路线.
此问题是多个推销员的最佳推销员回路问题.即在加权图G 中求顶点集V 的划分12,,,n V V V L ，将G 分成n 个生成子图[][][]12,,...,n G V G V G V ，使得
（1）顶点i V O ∈, i =1，2，3,…,n ；
（2）()G V V n i i ==Y 1 ；
（3）()(),max max i j i j
i i
C C C ωωαω-≤，其中i C 为i V 的导出子图[]i V G 中的最佳推销员回路，()i C ω为i C 的权，i ，j =1，2，3,…,n ；
（4）()1n
i i C ω=∑取最小.
定义 称()()()
,0max max i j i j
i i C C C ωωαω-=为该分组的实际均衡度.α为最大容
许均衡度.
显然100≤≤α，0α越小，说明分组的均衡性越好.取定一个α后，0α与α满足条件（3）的分组是一个均衡分组.条件（4）表示总巡视路线最短.
此问题包含两方面：第一，对顶点分组；第二，在每组中求最佳推销员回路，即为单个推销员的最佳推销员问题.
由于单个推销员的最佳推销员回路问题不存在多项式时间内的精确算法，故多个推销员的问题也不存在多项式时间内的精确算法.而图中节点数较多，为53个，我们只能去寻求一种较合理的划分准则，对图１进行粗步划分后，求出各部
分近似最佳推销员回路的权，再进一步调整，使得各部分满足均衡性条件（3）.
从O点出发去其他点，要使路程较小应尽量走O点到该点的最短路.故用图论软件包求出O点到其余顶点的最短路，这些最短路构成一棵以O为树根的树，将从O点出发的树枝称为干枝，见图2，从图中可以看出，从O点出发到其它点共有6条干枝，他们的名称分别为①，②，③，④，⑤，⑥.
根据实际工作的经验及上述分析，在分组时应遵从以下准则：
准则一：尽量使同一干枝及其分枝上的点分在同一组；
准则二：应将相邻的干枝上的点分在同一组；
准则三：尽量将长的干枝与短的干枝分在同一组.
由上述分组准则，我们找到两种分组形式如下：
分组一：（⑥，①），（②，③），（⑤，④）；
分组二：（①，②），（③，④），（⑤，⑥）．
显然分组一的方法极不均衡，故考虑分组二.
对分组二中每组顶点的生成子图，用算法一求出近似最优解及相应的巡视路线.使用算法一时，在每个子图所构造的完备图中，取一个尽量包含图2中树上的边的H圈作为其第2步输入的初始圈.
分组二的近似解见表1.
表1（单位：km）
小组
名称路线总路线长度路线的总长度
I O-P-28-27-26-N-24-23-22-17-16-I-15-I-18-K
-21-20-25-M-O 191.1
558.5
II O-2-5-6-L-19-J-11-G-13-14-H-12-F-10-F-9-
E-7-E
-8-4-D-3-C
241.9
III O-R-29-Q-30-32-31-33-35-34-A-B-1-O
125.5 图2 O点到任意点的最短路图（单位：km）
因为该分组的均衡度0α=()()()121,2,3
241.9125.5max 241.9i i C C C ωωω=--==54.2% 所以此分法的均衡性很差.
为改善均衡性，将第Ⅱ组中的顶点C ，2，3，D ，4分给第Ⅲ组（顶点2为这两组的公共点），重新分组后的近似最优解见表2.
因该分组的均衡度=0α()311,2,3
216.4191.1max 216.4i i C ω=-==11.69% 所以这种分法的均衡性较好.
问题二 当巡视人员在各乡（镇）、村的停留时间一定，汽车的行驶速度一定，要在24h 内完成巡视，至少要分几组及最佳的巡视路线.
由于T =2h ，t =1h ，V =35km/h ，需访问的乡镇共有17个，村共有35个.计算出在乡（镇）及村的总停留时间为17⨯2h+35h=69h ，要在24h 内完成巡回，若
不考虑行走时间，有: 2469<i
(i 为分的组数).得i 最小为4，故至少要分4组. 由于该网络的乡（镇）、村分布较为均匀，故有可能找出停留时间尽量均衡
的分组，当分4组时各组停留时间大约为69h 17.254
=h ，则每组分配在路途上的时间大约为24h-17.25h=6.75h.而前面讨论过，分三组时有个总路程599.8km 的巡视路线，分4组时的总路程不会比599.8km 大太多，不妨以599.8km 来计算.
路上时间约为599.8h 1735=h ，若平均分配给4个组，每个组约需4
17h=4.25h 〈6.75h ，故分成4组是可能办到的.
现在尝试将顶点分为4组.分组的原则：除遵从前面准则一、二、三外，还应遵从以下准则：
准则四：尽量使各组的停留时间相等.
用上述原则在图2上将图分为4组，同时计算各组的停留时间,然后用算法一算出各组的近似最佳推销员巡回，得出路线长度及行走时间，从而得出完成巡视的近似最佳时间.用算法一计算时，初始圈的输入与分3组时同样处理.
这4组的近似最优解见表3.
加框的表示此点只经过不停留.
该分组实际均衡度0α==-74
.2269.2174.22 4.62% 可以看出，表3分组的均衡度很好，且完全满足24h 完成巡视的要求.。
