案例：最佳灾情巡视路线

格式：ppt
大小：556.50 KB
文档页数：20

下载文档原格式

图论1

定义 1) 若H是赋权图G的一个子图，则称H的各边的权和 w( H ) w(e) 为H的权. 类似地，若
eE ( H )
若P(u,v)是赋权图G中从u到v的路,称 w( P) 称为路P的权．
eE ( P )
w(e)
2) 在赋权图G中，从顶点u到顶点v的具有最小权的路P*(u,v)，称为u到v的最短路． 3) 把赋权图G中一条路的权称为它的长，把(u,v) 路的最小权称为u和v之间的距离，并记作 d(u,v).
uavdxcw 路或路径：
圈或回路：uavbwcxfygu
3．最短路问题及算法
最短路问题是图论应用的基本问题，很多实际问题，如线路的布设、运输安排、运输网络最小费用流等问题,都可通过建立最短路问题模型来求解. •最短路的定义 •最短路问题的两种方法：Dijkstra和Floyd算法 . 1) 求赋权图中从给定点到其余顶点的最短路. 2) 求赋权图中任意两点间的最短路.
例设 H (V ( H ), E ( H )) ，其中：
V ( H ) {u1, u2 , u3 , u4 , u5}，
E ( H ) {a1, a2 , a3 , a4 , a5 , a6 , a7 }， a1 (u1, u2 ) ， a2 (u2 , u2 ) ， a3 (u4 , u2 ) ，
（见图 2）
定义若一个图的顶点集和边集都是有限集，则称其为有限图. 只有一个顶点的图称为平凡图，其他的
所有图都称为非平凡图.
定义若图G中的边均为有序偶对 (vi , v j ),称G为有向图. 称边 e (vi , v j ) 为有向边或弧,称 e (vi , v j )是从vi 连接 v j ，称 vi为e的尾，称 v j为e的头. 若图G中的边均为无序偶对 vi v j ，称G为无向图.称边 e vi v j 为无向边，称e连接 vi 和 v j，顶点 vi 和 v j 称为e的端点. 既有无向边又有有向边的图称为混合图.

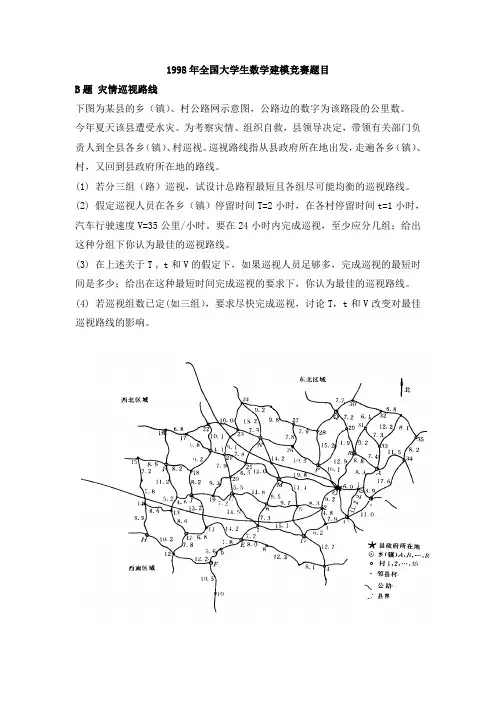
1998年全国大学生数学建模竞赛题

1998年全国大学生数学建模竞赛题目B题灾情巡视路线下图为某县的乡（镇）、村公路网示意图，公路边的数字为该路段的公里数。

今年夏天该县遭受水灾。

为考察灾情、组织自救，县领导决定，带领有关部门负责人到全县各乡（镇）、村巡视。

巡视路线指从县政府所在地出发，走遍各乡（镇）、村，又回到县政府所在地的路线。

(1) 若分三组（路）巡视，试设计总路程最短且各组尽可能均衡的巡视路线。

(2) 假定巡视人员在各乡（镇）停留时间T=2小时，在各村停留时间t=1小时，汽车行驶速度V=35公里/小时。

要在24小时内完成巡视，至少应分几组；给出这种分组下你认为最佳的巡视路线。

(3) 在上述关于T , t和V的假定下，如果巡视人员足够多，完成巡视的最短时间是多少；给出在这种最短时间完成巡视的要求下，你认为最佳的巡视路线。

(4) 若巡视组数已定(如三组），要求尽快完成巡视，讨论T，t和V改变对最佳巡视路线的影响。

灾情巡视路线模型摘要本文将求最佳巡视路线间题转化为图论中求最佳推销员回路（哈米尔顿回路）的问题,并用近似算法去寻求近似最优解。

对赋权图中的路径分组问题定义了均衡度用以衡量分组的均衡性。

对问题1和问题2先定出几个分的准则进行初步分组,并用近似算法求每一组的近似最佳推销员回路,再根据均衡度进行微调,得到较优的均衡分组和每组的近似最佳推销员回路。

对问题1，运用求任意两点间最短路的Floyd算法,得出总路程较短且各组尽可能均衡的路线,各组的巡视路程分别为216.4公里,191.1公里,192.3公里,总路程599.8公里。

对问题2,证明了应至少分为4组,并求出了分为4组时各组的较优巡视路线,各组的巡视时间分别为22.74小时,22.59小时,21.69小时,22.54小时。

对问题3,求出完成巡视的最短时间为6.43小时,并用较为合理的分组的准则,分成22个组对问题4，研究了在不影响分组的均衡条件下, T,t,V的允许变化范围,并得出了这三个变量的关系式,并由此对分三个组的情况进行了具体讨论。

灾情巡视路线

各组所走的路程分别为（单位：km）：212.2、125.5、215.9，各组所走的路程总和为（单位：km）：553.6，并求出其均衡度为：0.49。 4.2 问题二 4.2.1 问题分析与第一题相同，将巡视人员分为几组便将区域划分为几个部分。因此我们首先确定在 24 小时内至少需要将巡视人员分为几组。在划分区域的过程中，经过观察与计算发现，图中乡、村的分布十分的均匀，不存在某个区域集中出现乡或者镇，因此可以忽略停留时间对最小生成树与深度搜索的影响。所以我们套用第一问的模型。先进行粗略的分割得到大致所需的路程，然后根据最小生成树进行深度优先算法，得到精确的路径，根据路径算出各组所需时间以及总时间。 4.2.2 模型的求解首先计算需要把巡视人员分为几组：乡镇停留时间:T=2 小时,村镇停留时间:t=1 小时,车速:V=35 公里/小时,乡镇共有 17 个，村镇有 35 个, 总停留时间为 17×2+35=69 小时，要在 24 小时内完成巡回，若不考虑汽车行驶时间，由 69/i<24(i 为分的组数)得到 i 最小为 4，故至少要分 4 组。由于该网络的乡(镇)、村分布较为均匀,故有可能找出停留时间尽量均衡的分组,当分 4 组时各组停停留时间大约为 69/4=17.25 小时，则每组分配在路途上的时间大约为 24-17.25=6.75 小时。根据第一问, 分三组时有个总巡视路程 602 公里，分 4 组时的总路程不会比 603 公里大太多 , 不妨以 603 公里作为第二问的巡视总路程。路上约花 603/35=17 小时,若平均分配给 4 个组,每个组约需 17/4=4.25 小时小于 6.75 小时,故巡视路线分成 4 组是合理的。接下来套用第一题的最小生成树的 DFS 模型，得出了以下四个分组的路径：

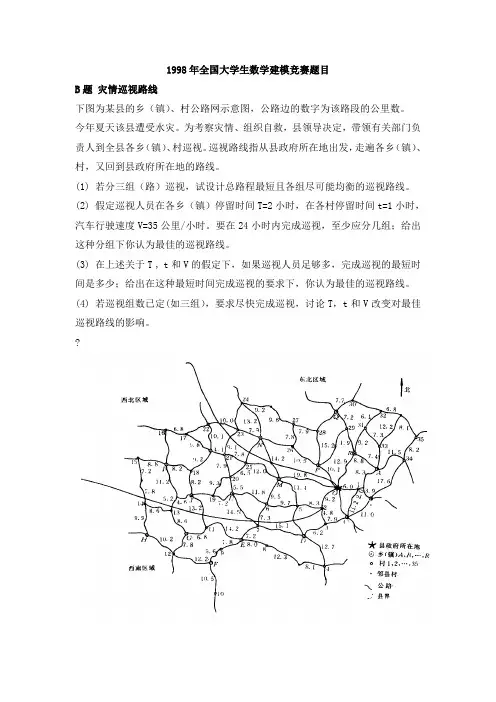
1998年全国大学生数学建模竞赛题

1998年全国大学生数学建模竞赛题目B题灾情巡视路线下图为某县的乡（镇）、村公路网示意图，公路边的数字为该路段的公里数。

今年夏天该县遭受水灾。

为考察灾情、组织自救，县领导决定，带领有关部门负责人到全县各乡（镇）、村巡视。

巡视路线指从县政府所在地出发，走遍各乡（镇）、村，又回到县政府所在地的路线。

(1) 若分三组（路）巡视，试设计总路程最短且各组尽可能均衡的巡视路线。

(2) 假定巡视人员在各乡（镇）停留时间T=2小时，在各村停留时间t=1小时，汽车行驶速度V=35公里/小时。

要在24小时内完成巡视，至少应分几组；给出这种分组下你认为最佳的巡视路线。

(3) 在上述关于T , t和V的假定下，如果巡视人员足够多，完成巡视的最短时间是多少；给出在这种最短时间完成巡视的要求下，你认为最佳的巡视路线。

(4) 若巡视组数已定(如三组），要求尽快完成巡视，讨论T，t和V改变对最佳巡视路线的影响。

?灾情巡视路线模型摘要本文将求最佳巡视路线间题转化为图论中求最佳推销员回路（哈米尔顿回路）的问题,并用近似算法去寻求近似最优解。

对赋权图中的路径分组问题定义了均衡度用以衡量分组的均衡性。

对问题1，运用求任意两点间最短路的Floyd算法,得出总路程较短且各组尽可能均衡的路线,各组的巡视路程分别为公里,公里,公里,总路程公里。

对问题2,证明了应至少分为4组,并求出了分为4组时各组的较优巡视路线,各组的巡视时间分别为小时,小时,小时,小时。

对问题3,求出完成巡视的最短时间为小时,并用较为合理的分组的准则,分成22个组对问题4，研究了在不影响分组的均衡条件下, T,t,V的允许变化范围,并得出了这三个变量的关系式,并由此对分三个组的情况进行了具体讨论。

关键词：最佳推销员回路问题哈米尔顿回路赋权图近似算法均衡度一、问题重述1998年夏天某县遭受水灾。

最佳灾情巡视路线模型

最佳灾情巡视路线模型【摘要】“图论”是组合数学的分支，它与其他的数学分支，如群论、矩阵论、拓扑学，数值分析有着密切的联系。

在其它科学领域，如计算机科学、运筹学、电网络分析、化学物理以及社会科学等方面图论也具有越来越重要的地位，并已取得丰硕的成果。

而且，图论的理论和方法在数学建模中也有重要应用。

本文概述了一些常用的图论方法和算法，并通过举例（灾情巡视路线）说明其在数学建模中的应用。

【关键词】图论灾情巡视Hamilton回路数学模型预备知识定义1 完全图：如果图G中每一对不同的顶点恰有一条边连接，则称此图为完全图。

定义2 连通图：如果对图G=（V，E）的任何两个顶点u与v，G中存在一条（u-v）路。

则称G是连通图。

定义3 加权图：边上有数的图称为加权图。

在加权图中，链（迹、路）的长度为链（迹、路）上的所有边的权植的和。

定义4 Hamilton回路：图G中的一个回路C称为一个Hamilton回路如果C含有G 的所有顶点。

含有Hamilton回路的图称为Hamilton图。

定义5 欧拉回路：经过图G的每条边的迹称为欧拉迹，如果这条迹是闭的，则称这条闭迹为G的欧拉回路。

一数学建模中常用的图论方法1 迪克斯特拉算法（Dijkstra）1.1问题来源在加权图中，我们经常需要找出两个指定点之间的最短路，通常称为最短路问题。

解决最短路问题的方法之一就是迪克斯特拉算法。

1.2基本思路假定P：V1→V2→ (V)i→…→Vj→…→Vk是从V1到Vk的最短路，则它的子路Vi →…→Vj一定是从Vi到Vj的最短路。

否则从V1出发沿路p走到Vi，,然后沿Vi 到Vj的最短路走到Vj再沿路P从Vj到Vk，这样得到一条新的从V1出发到Vk的路，其长度小于P，与P是最短路的假设矛盾。

1.3算法设G为所有权都为正数的加权连通简单图。

G带有顶点a=V0, V1, (V)n=z,权W(Vi , Vj) ,若(Vi, Vj)不是G中的边，则W(Vi, Vj) =∞for i=1 to nL((Vi)= ∞L(a)=0S=Ф(初始化标记，a的标记为0，其它结点标记为∞，S 为空集)当z不属于S时beginu=不属于S的L（u）最小的一个顶点S=S∪{u}对所有不属于S的顶点Vif L(u)+W(u,v)<L(v) thenL(v)=L(u)+L(u,v) (这样就给S中添加带最小标记的顶点并且更新不在S中的顶点的标记)End (L(z)表示从a到z的最短路的长度) 这个算法经过n-1次循环后必定结束，计算量为1/2（n-1）(n-2)，因而是个有效算法。

数模论文之灾情巡视路线

数模论文之灾情巡视路线（相对优化方案）嘿，各位亲爱的数模爱好者，今天我们来聊聊灾情巡视路线的优化方案。

这个问题可是关系到救援效率和灾民生命安全的头等大事，咱们可得好好研究研究。

先来分析一下现有的巡视路线。

一般来说，现有的路线都是按照行政区域划分，从A点到B点，再到C点，看似合理，但实际上存在很多问题。

比如说，路线过长，导致救援队伍无法在第一时间赶到现场；路线规划不合理，有时候会绕弯路，浪费时间；还有，巡视路线上的重点区域划分不清，容易导致救援资源分配不均。

那怎么办呢？咱们得来个相对优化方案。

下面我就用意识流的方式，给大家详细讲解一下这个方案。

我们要运用图论的知识，对初步的巡视路线进行优化。

具体操作如下：1.将受灾点视为图的节点，受灾点之间的距离视为图的边，建立一张灾情巡视图。

2.运用Dijkstra算法，计算从救援队伍出发点到各个受灾点的最短路径。

3.对最短路径进行排序，优先考虑受灾程度较高的区域。

4.根据道路状况和救援队伍的行动速度，调整路径顺序，使得救援队伍在巡视过程中能够高效地到达各个受灾点。

5.对优化后的巡视路线进行评估，包括救援时间、救援成本、救援效果等方面，确保方案的科学性和实用性。

在这个过程中，我们还要考虑到一些特殊情况。

比如说，有些受灾点因为地形原因，无法直接到达，这时候我们可以采用无人机等先进设备进行巡视。

再比如，有些受灾点之间可能存在交通管制，这时候我们需要及时调整路线，确保救援队伍能够顺利到达。

优化方案有了，就是实施阶段。

我们要与政府部门、救援队伍、志愿者等各方密切配合，确保方案的顺利实施。

具体操作如下：1.制定详细的实施方案，明确各部门的职责和任务。

2.建立一个灾情信息共享平台，实时更新受灾点的受灾情况和救援进度。

3.对救援队伍进行培训，提高他们的救援技能和应对突发事件的能力。

4.加强宣传，提高公众对灾情巡视路线优化方案的认识和支持。

5.定期对方案进行评估和调整，以适应不断变化的灾情和救援需求。

问题引入与分析

G[{v1,v2,v3}] G[{e3,e4,e5,e6}]
3) 若 V V，且 V ，以 V 为顶点集，以两端点均在V 中旳边旳全体为边集旳图 G 旳子图，称为G旳由V 导出旳子图，记为 G[V ] .
4) 若E E，且 E ，以 E为边集，以 E 旳端点集为顶点集旳图 G 旳子图，称为 G 旳由E 导出旳
0 0 1 0 0 v5
2) 对有向图 G (V , E) ,其邻接矩阵 A (aij ) ,其中：
1, aij 0,
若(vi ,v j ) E, 若(vi ,v j ) E.
u1 u2
0 1 A 0 0
0 1 0 0
u3 u4
1 1 u1 0 0 u2 0 0 u3 1 0 u4
3) 对有向赋权图 G (V , E) , 其邻接矩阵 A (aij ) ,
若图G中旳边均为无序偶对 viv j，称G为无向图.称边e viv j 为无向边，称e连接vi 和 v j，顶点 vi 和v j 称为e旳端点. 既有无向边又有有向边旳图称为混合图.
例设H (V (H ), E(H ))，其中： V (H ) {u1,u2,u3,u4,u5}， E(H ) {a1, a2, a3, a4, a5, a6, a7}， a1 (u1,u2) ， a2 (u2,u2) ， a3 (u4,u2 ) ， a4 (u4,u5) ， a5 (u4,u3) ， a6 (u3,u4 ) ， a7 (u1,u3). （见右图 3）
d (u3) 3
5) 路和连通
定义1) 无向图G旳一条途径（或通道或链）是指一种有限非空序列 W v0e1v1e2 ekvk ，它旳项交替地为顶点和边，使得对 1 i k，ei旳端点是vi1和 vi, 称W是从v0到 vk 旳一条途径，或一条 (v0,vk ) 途径. 整数k称为W旳长. 顶点 v0 和 vk 分别称为旳起点和终点 , 而 v1,v2,,vk1称为W旳内部顶点.

灾情巡视的数学模型

灾情巡视的数学模型摘要本文解决的是对全县各乡镇和村庄的灾情巡视问题，要求到达每一个乡镇和村庄，属于点的遍历性的旅行推销员问题。

有所不同的是要考虑不同组的均衡。

所以我们建立了约束最优路线模型，虽然在处理该问题上不能得到精确的值，但是可以通过遗传算法得出求得较好的近似解。

得出相对最优的巡视分配和路线选择方案，结果令人满意。

对于问题一：对于问题二：对于问题三：对于问题四：【关键词】约束最优路线遗传算法1. 问题重述今年夏天某县遭受水灾，为考察灾情、组织自救，县领导决定，带领有关部门负责人到全县各乡（镇）、村巡视，巡视路线指从县政府所在地出发，走遍各乡（镇）、村，又回到县政府所在地的路线。

下图为某县的乡（镇）、村公路网示意图，公路边的数字为该路段的公里数。

附：图中节点间距如下所示：(X 节点,Y 节点,x 与y 间距)(16,17,6.8) (16,i,11.8) (15,i,8.8) (i,18,8.2) (17,k,9.8) (17,22,6.7)(22,k,10.1) (22,23,10.0) (21,23,9.1) (21,k,4.1) (21,25,7.8) (23,n,7.9) (23,24,8.9) (24,n,13.2) (25,n,8.8) (25,20,6.5) (21,20,7.9) (18,j,8.2) (18,k,9.2) (14,13,8.6) (14,h,9.9) (h,12,10.2) (12,f,12.2) (12,g,7.8) (13,g,8.6) (g,11,6.8) (j,11,13.2) (j,19,8.1) (19,L,7.2) (19,20,9.3) (11,e,14.2) (f,10,10.8)(f,9,5.6) (9,e,7.8) (e,8,8.0) (e,7,7.2) (L,7,14.5) (L,6,11.8) (7,6,7.3) (7,d,15.2) (d,4,12.7) (5,d,11.3) (6,5,9.7) (6,m,9.5)(25,m,12.0) (n,m,14.2) (n,26,10.5) (27,26,7.8) (27,28,7.9) (26,p,10.5) (28,p,12.1) (28,q,8.3) (q,30,7.7) (30,32,10.3) (q,29,7.2) (p,29,15.2) (m,o,19.8) (m,5,11.4) (5,2,8.3) (d,3,8.2) (3,c,7.9) (2,3,4.8) (2,o,9.2) (o,c,11.5) (o,1,60) (p,o,10.1) (o,r,12.9) (29,r,7.9) (31,r,9.2) (31,32,8.2) (33,32,19.0) (31,33,7.3) (33,a,7.4) (r,a,8.8) (a,34,11.5) (a,1,10.3) (a,b,12.2) (1,b,5.9) (1,c,11.2) (b,c,11.1) (8,4,20.4) (15,14,15.0)(i,13,16.4) (i,j,15.8) (13,j,9.8) (L,20,5.5) (24,27,18.8) (32,35,14.9) (33,35,20.3) (34,35,8.2) (34,b,17.6)本文需解决的问题有：问题一：若分三组（路）巡视，试设计总路程最短且各组尽可能均衡的巡视路线。

1998年全国大学生数学建模竞赛题之欧阳科创编

1998年全国大学生数学建模竞赛题目创作：欧阳科B题灾情巡视路线下图为某县的乡（镇）、村公路网示意图，公路边的数字为该路段的公里数。

今年夏天该县遭受水灾。

为考察灾情、组织自救，县领导决定，带领有关部门负责人到全县各乡（镇）、村巡视。

巡视路线指从县政府所在地出发，走遍各乡（镇）、村, 又回到县政府所在地的路线。

（1）若分三组（路）巡视，试设计总路程最短且各组尽可能均衡的巡视路线。

⑵ 假定巡视人员在各乡（镇）停留时间T二2小时，在各村停留时间t=l小时，汽车行驶速度V二35公里/小时。

要在24小时内完成巡视，至少应分几组；给出这种分组下你认为最佳的巡视路线。

（3）在上述关于T ,上和^的假定下，如果巡视人员足够多，完成巡视的最短时间是多少；给出在这种最短时间完成巡视的要求下，你认为最佳的巡视路线。

（4）若巡视组数已定（如三组），要求尽快完成巡视，讨论T, t和V改变对最佳巡视路线的影响。

灾情巡视路线模型摘要本文将求最佳巡视路线间题转化为图论中求最佳推销员回路（哈米尔顿回路）的问题，并用近似算法去寻求近似最优解。

对赋权图中的路径分组问题定义了均衡度用以衡量分组的均衡性。

对问题1和问题2先定出几个分的准则进行初步分组，并用近似算法求每一组的近似最佳推销员回路，再根据均衡度进行微调，得到较优的均衡分组和每组的近似最佳推销员回路。

对问题1,运用求任意两点间最短路的Floyd算法,得出总路程较短且各组尽可能均衡的路线，各组的巡视路程分别为216.4公里,191.1公里,192.3公里,总路程599.8公里。

对问题2,证明了应至少分为4组,并求出了分为4组时各组的较优巡视路线，各组的巡视时间分别为22.74小时,22.59小时,21.69小时,22.54小时。

对问题3,求出完成巡视的最短时间为6.43小时,并用较为合理的分组的准则，分成22个组对问题4,研究了在不影响分组的均衡条件下,T,t,V 的允许变化范围，并得出了这三个变量的关系式，并由此对分三个组的情况进行了具体讨论。

旅行商问题(TSP)

表示连接两城市的路，边上的权W（e）表示距
离（或时间或费用）。于是旅行推销员问题就
成为在加权图中寻找一条经过每个顶点正好一
次的最短圈的问题，即求最佳Hamilton 圈的
问题。
基本概念
•： 1) 哈米尔顿路径(H路径): 经过图G每个顶点正好一次的路径; 2) 哈米尔顿圈(H圈)；经过G的每个顶点正好一次的圈; 3) 哈米尔顿图(H图): 4) 最佳H圈: 含H圈的图。
到的C即为所求。
例对下图的K6,用二边逐次修正法求较优H圈.
较优H圈:
C3 v1v4v5v6v2v3v1
其权为W(C3)=192
分析: 这个解的近似程度可用最优H圈的权的下界与其比较而得出.即利用最小生成树可得最优H圈的一个下界. 设C是G的一个最优H圈，则对G的任一顶点v, C-v是 G-v的生成树.如果T是G-v的最小生成树,且e1是e2与v关联的边中权最小的两条边,则w(T)+w(e1)+w(e2)将是w(C) 的一个下界. 取v=v3,得G-v3的一最小生成树(实线),其权 w(T)=122,与v3关联的权最小的两条边为v1v3和v2v3, 故w(C) w(T)+w(v1v3)+w(v2v3) =178. 故最优H圈的权应满足178 w(C) 192.
参考书： 1.龚劬《图论与网络最优化算法》重庆大学出版社,2009 2.西北工业大学数学建模指导委员会《数学建模简明教程》高等教育出版社
主讲：重庆大学龚劬
主要内容
引例基本概念 TSP模型的应用算法简介最佳灾情巡视路线的模型的建立与求解
引例
•：
1. 98年全国大学生数学建模竞赛B题“最佳灾情巡视路线”中的前两个问题：今年(1998年)夏天某县遭受水灾. 为考察灾情、

灾区巡视--最佳路线-选择问题-数学建模

灾难最佳巡视路线摘要本文解决的是对全县的乡镇和村庄进行灾情巡视最佳线路的求解问题，多旅行售货问题。

问题一是三个旅行售货问题，问题二是四个旅行售货问题。

我们可以运用图论的知识并且考虑气均衡性，建立起约束最优化线路模型来解决这个问题。

关键词：Hamilton圈多旅行售货问题最小生成树问题今年夏天该县遭受水灾。

为考察灾情、组织自救，县领导决定，带领有关部门负责人到全县各乡（镇）、村巡视。

巡视路线指从县政府所在地出发，走遍各乡（镇）、村，又回到县政府所在地的路线。

1.若分三组（路）巡视，试设计总路程最短且各组尽可能均衡的巡视路线。

2.假定巡视人员在各乡（镇）停留时间T=2小时，在各村停留时间t=1小时，汽车行驶速度V=35公里/小时。

要在24小时内完成巡视，至少应分几组；给出这种分组下你认为最佳的巡视路线。

1.问题重述问题1：若分三组（路）巡视，试设计总路程最短且各组尽可能均衡的巡视路线图问题2：假定巡视人员在各乡（镇）停留时间T=2小时，在各村停留时间t=1小时，汽车行驶速度V=35公里/小时。

要在24小时内完成巡视，至少应分几组；给出这种分组下你认为最佳的巡视路线。

问题3：在上述关于T , t和V的假定下，如果巡视人员足够多，完成巡视的最短时间是多少；给出在这种最短时间完成巡视的要求下，你认为最佳的巡视路线。

问题4：若巡视组数已定(如三组），要求尽快完成巡视，讨论T，t和V改变对最佳巡视路线的影响。

2.模型的假设及符号说明2.1模型假设假设1：假设汽车在路上以V匀速行驶，且不停留，不考虑故障，忽略外部因素影响假设2：巡视过程中除了正常停留外，没有因其它因素造成时间延误假设3：巡视路线可以重复假设4：对于要多次经过的乡(镇)或村只停留一次假设5：每个巡视人员只能走自己划分区域内的路线2.2符号说明G：表示加权图Gi：表示子图V：表示顶点，每一个乡(镇)或村看成一个点E：表示边，乡(镇)或村之间的路线w(x，y)：表示权重，乡(镇)或村之间的距离S：表示回路路程总和ə：表示路程均衡度Li：表示每一条子回路T：表示在每个乡(镇)停留的时间I：表示在每个村停留的时间Ti：表示第i组的巡视时间V：表示汽车行驶速度Z：表示划分的区域数N：表示乡(镇)的数目N：表示村的数目Ni：表示第i组巡视乡(镇)的数目Ni：表示第i组巡视村的数目M：表示所分的组数v ：表示时间均衡度3.问题分析本文研究的是最佳巡视路线设计问题，要求从O点出发巡视完所有乡(镇)村后，在回到O点，此问题可以转化为旅行商问题，再设计相应的算法求解针对问题一：问题一要求设计3组巡视总路程最短且尽可能均衡，首先我们通过主观筛选法将原图划分为3个子图，每个子图顶点数大约为17个，相邻的点划在一个子图中，且尽量使每个子图构成一个回路，这样将原问题转化为单旅行商问题求解针对问题二：问题二在问题一的基础上加了时间的限制，在每一个顶点都有停留时间，且在24小时巡视完。

案例：最佳灾情巡视路线共22页

故用软件包求出O点到其余顶点的最短路. 这些最短路构成一棵O为树根的树. 将从O点出发的树枝称为干枝.
准在则由分1 上尽组述量时分使应组同遵准一从则干准，枝则我上：们及找其到分两枝种上分的组点形分式在如同下一：组. 准分则从组2O1点应:（出将⑥发相，到邻①其的）它干，点枝（共上②有的，6点条③分干）在枝，同，（一它⑤组们，；的④名）称分准分别则组为32尽①:（量，①将②，长，②的③）干，，枝④（与，③短⑤，的，④干⑥）枝. ，分（在⑤同，一⑥组）. 分组1极不均衡,故考虑分组2.
解决此类问题的一般方法是不现实的，对于规模较大
的问题可使用近似算法来求得近似最优解.
6. 最佳灾情巡视路线的模型的建立与求解
问题转化为在给定的加权网络图中寻找从
给定点O出发, 行遍所有顶点至少一次再回回到点O ,使得总权(路程或时时间)最小,即最佳旅行售货员问题.
近证第因似最能2二)算佳得，边法旅到3逐)求行，较次其售4优修)一货步的正个员分计法近问别算的似题用结结最是三果果优N种. 与P解方—初，法完始来产全圈代生问有替初题关最始,,采故优圈用本解，一算.以种法保算法一求加权图的最佳旅行售货员回路近似算法:
修正法进行优化，得到近似最优H圈；
6) 在第5)步求出的所有H圈中，找出权最小的一个, 此即要找的最优H圈的近似解.
问题一若分为三组巡视，设计总路程最短且各
组尽可能均衡的巡视路线.
此问题是多个售货员的最佳旅行售货员问题.
即在加权图G中求顶点集V 的划分V1,V2,,Vn，将G
分成 n 个生成子图G[V1], G[V2 ],, G[Vn
1) 顶点O Vi, i 1,2,3,,n. 2)
]，使得
n Vi V

灾情巡视路线的数学模型

灾情巡视路线的数学模型摘要本文解决的是灾情巡视路线的设计问题。

由于路线图可看成网络图因此此问题可转化为在给定的加权网络图中寻找从给定点Ｏ出发行遍所有顶点至少一次再回到点Ｏ使得总权（路程或时间）最小的问题。

然后针对具体问题，采用一些启发式算法，建立模型进行求解。

对于问题一：基于设计分三组巡视时使总路程最短且各组尽可能均衡的巡视路线的要求我们采用Dijkstra算法，通过对初始圈进行二边逐次修正,处理三组的巡视路线长度，用lingo软件求解出较优方案。

定义分组的均衡度系数a检验分组均衡度，在均衡度为a=0.0751时得到分三组（路）巡视时，总路程最短且各组尽可能均衡的巡视路线见附表1。

对于问题二：将问题转化为图论问题，运用问题一的求解方法，得到分为四组的路线，在通过均衡度分析之后得出近似最优巡视路线。

利用lingo软件求得，至少要分四组，且四组的近似最优巡视路线见附表2。

对于问题三：基于问题一二中图论的方法，考虑到从Ｏ点巡视H点的最短时间是所有巡视线路中用时最长的，将计算出的最长路线巡视所用的时间作为巡视路线的最短时间限定，在此限定下对路线进行设计。

求得的最短时间为6.43小时，最佳巡视路线分为23组。

（具体分组见附录二）对于问题四：由于组数一定， T，t和V改变，对每组内的最佳巡视路线是没有影响的，但可能会影响到各组件的均衡性，因此问题实质是讨论T，t和V对分组的影响，即在不破坏原来分组均衡的条件下T，t和V允许的最大变化范围。

关键词：启发式算法 Dijkstra算法均衡度图论二边逐次修正1. 问题重述1.1问题背景今年夏天某县遭受水灾。

为考察灾情、组织自救，县领导决定，带领有关部门负责人到全县各乡（镇）、村巡视。

巡视路线指从县政府所在地出发，走遍各乡（镇）、村，又回到县政府所在地的路线。

附录一中给出了该县的乡（镇）、村公路网示意图，公路边的数字为该路段的公里数。

1.2本文需解决的问题问题一：若分三组（路）巡视，试设计总路程最短且各组尽可能均衡的巡视路线。

1998年全国大学生数学建模竞赛题

1998年全国大学生数学建模竞赛题目B题灾情巡视路线下图为某县的乡（镇）、村公路网示意图，公路边的数字为该路段的公里数。

今年夏天该县遭受水灾。

为考察灾情、组织自救，县领导决定，带领有关部门负责人到全县各乡（镇）、村巡视。

巡视路线指从县政府所在地出发，走遍各乡（镇）、村，又回到县政府所在地的路线。

(1) 若分三组（路）巡视，试设计总路程最短且各组尽可能均衡的巡视路线。

(2) 假定巡视人员在各乡（镇）停留时间T=2小时，在各村停留时间t=1小时，汽车行驶速度V=35公里/小时。

要在24小时内完成巡视，至少应分几组；给出这种分组下你认为最佳的巡视路线。

(3) 在上述关于T , t和V的假定下，如果巡视人员足够多，完成巡视的最短时间是多少；给出在这种最短时间完成巡视的要求下，你认为最佳的巡视路线。

(4) 若巡视组数已定(如三组），要求尽快完成巡视，讨论T，t和V改变对最佳巡视路线的影响。

灾情巡视路线模型摘要本文将求最佳巡视路线间题转化为图论中求最佳推销员回路（哈米尔顿回路）的问题,并用近似算法去寻求近似最优解。

对赋权图中的路径分组问题定义了均衡度用以衡量分组的均衡性。

对问题2,证明了应至少分为4组,并求出了分为4组时各组的较优巡视路线,各组的巡视时间分别为22.74小时,22.59小时,21.69小时,22.54小时。

灾情巡视路线程序

9附录附录一：Kruskal最小树成法程序clear all%图论最小生成树Kruskal避圈算法%w为邻接矩阵w=[0 inf inf inf inf inf inf inf inf inf inf inf inf inf inf inf inf inf inf inf inf inf inf inf inf inf inf inf inf inf inf inf inf inf inf 10.3 5.9 11.2 inf inf inf inf inf inf inf inf inf inf inf 6 inf inf inf ; inf 0 4.8 inf 8.3 inf inf inf inf inf inf inf inf inf inf inf inf inf inf inf inf inf inf inf inf inf inf inf inf inf inf inf inf inf inf inf inf inf inf inf inf inf inf inf inf inf inf inf inf 8.2 inf inf inf ;inf 4.8 0 inf inf inf inf inf inf inf inf inf inf inf inf inf inf inf inf inf inf inf inf inf inf inf inf inf inf inf inf inf inf inf inf inf inf 7.8 8.2 inf inf inf inf inf inf inf inf inf inf inf inf inf inf ;inf inf inf 0 inf inf inf 20.4 inf inf inf inf inf inf inf inf inf inf inf inf inf inf inf inf inf inf inf inf inf inf inf inf inf inf inf inf inf inf 12.7 inf inf inf inf inf inf inf inf inf inf inf inf inf inf ; inf 8.3 inf inf 0 inf inf inf inf inf inf inf inf inf inf inf inf inf inf inf inf inf inf inf inf inf inf inf inf inf inf inf inf inf inf inf inf inf 11.3 inf inf inf inf inf inf inf inf 11.4 inf inf inf inf inf ; inf inf inf inf 9.7 0 7.3 inf inf inf inf inf inf inf inf inf inf inf inf inf inf inf inf inf inf inf inf inf inf inf inf inf inf inf inf inf inf inf inf inf inf inf inf inf inf inf 11.8 9.5 inf inf inf inf inf ; inf inf inf inf inf 7.3 0 inf inf inf inf inf inf inf inf inf inf inf inf inf inf inf inf inf inf inf inf inf inf inf inf inf inf inf inf inf inf inf 15.1 7.2 inf inf inf inf inf inf 14.5 inf inf inf inf inf inf ; inf inf inf 20.4 inf inf inf 0 inf inf inf inf inf inf inf inf inf inf inf inf infinf inf inf inf inf inf inf inf inf inf infinf inf inf inf inf inf inf 8 inf inf infinf inf inf inf inf inf inf inf inf inf ;inf inf inf inf inf inf inf inf 0 inf infinf inf inf inf inf inf inf inf inf inf infinf inf inf inf inf inf inf inf inf inf infinf inf inf inf inf inf 7.8 5.6 inf inf infinf inf inf inf inf inf inf inf inf ;inf inf inf inf inf inf inf inf inf 0 infinf inf inf inf inf inf inf inf inf inf infinf inf inf inf inf inf inf inf inf inf infinf inf inf inf inf inf inf 10.8 inf infinf inf inf inf inf inf inf inf inf inf ;inf inf inf inf inf inf inf inf inf inf 0 inf inf inf inf inf inf inf inf inf inf infinf inf inf inf inf inf inf inf inf inf infinf inf inf inf inf inf 14.2 inf 6.8 infinf 13.2 inf inf inf inf inf inf inf inf ;inf inf inf inf inf inf inf inf inf inf inf0 inf inf inf inf inf inf inf inf inf infinf inf inf inf inf inf inf inf inf inf infinf inf inf inf inf inf inf 12.2 7.8 10.2 inf inf inf inf inf inf inf inf inf inf ;inf inf inf inf inf inf inf inf inf inf infinf 0 8.6 inf inf inf inf inf inf inf infinf inf inf inf inf inf inf inf inf inf infinf inf inf inf inf inf inf inf 8.8 inf 16.4 9.8 inf inf inf inf inf inf inf inf ;inf inf inf inf inf inf inf inf inf inf infinf 8.6 0 15 inf inf inf inf inf inf infinf inf inf inf inf inf inf inf inf inf infinf inf inf inf inf inf inf inf inf 9.9 infinf inf inf inf inf inf inf inf inf ;inf inf inf inf inf inf inf inf inf inf infinf inf 15 0 inf inf inf inf inf inf infinf inf inf inf inf inf inf inf inf inf infinf inf inf inf inf inf inf inf inf inf 8.8inf inf inf inf inf inf inf inf inf ;inf inf inf inf inf inf inf inf inf inf infinf inf inf inf 0 6.8 inf inf inf inf infinf inf inf inf inf inf inf inf inf inf infinf inf inf inf inf inf inf inf inf inf 11.8 inf inf inf inf inf inf inf inf inf ;inf inf inf inf inf inf inf inf inf inf infinf inf inf inf 6.8 0 inf inf inf inf 6.7inf inf inf inf inf inf inf inf inf inf infinf inf inf inf inf inf inf inf inf inf infinf 9.8 inf inf inf inf inf inf inf ;inf inf inf inf inf inf inf inf inf inf infinf inf inf inf inf inf 0 inf inf inf infinf inf inf inf inf inf inf inf inf inf infinf inf inf inf inf inf inf inf inf inf 8.28.2 9.2 inf inf inf inf inf inf inf ;inf inf inf inf inf inf inf inf inf inf infinf inf inf inf inf inf inf 0 9.3 inf infinf inf inf inf inf inf inf inf inf inf infinf inf inf inf inf inf inf inf inf inf inf8.1 inf 7.2 inf inf inf inf inf inf ;inf inf inf inf inf inf inf inf inf inf infinf inf inf inf inf inf inf 9.3 0 7.9 infinf inf 6.5 inf inf inf inf inf inf inf infinf inf inf inf inf inf inf inf inf inf infinf inf 5.5 inf inf inf inf inf inf ;inf inf inf inf inf inf inf inf inf inf infinf inf inf inf inf inf inf inf 7.9 0 inf9.1 inf 7.8 inf inf inf inf inf inf inf infinf inf inf inf inf inf inf inf inf inf infinf 4.1 inf inf inf inf inf inf inf ;inf inf inf inf inf inf inf inf inf inf infinf inf inf inf inf 6.7 inf inf inf inf 0 10 inf inf inf inf inf inf inf inf inf inf infinf inf inf inf inf inf inf inf inf inf inf 10.1 inf inf inf inf inf inf inf ;inf inf inf inf inf inf inf inf inf inf infinf inf inf inf inf inf inf inf inf 9.1 100 8.9 inf inf inf inf inf inf inf inf infinf inf inf inf inf inf inf inf inf inf infinf inf inf inf 7.9 inf inf inf inf ;inf inf inf inf inf inf inf inf inf inf inf inf inf inf inf inf inf inf inf inf inf inf8.9 0 inf inf 18.8 inf inf inf inf infinf inf inf inf inf inf inf inf inf inf infinf inf inf inf inf 13.2 inf inf inf inf ;inf inf inf inf inf inf inf inf inf inf infinf inf inf inf inf inf inf inf 6.5 7.8 infinf inf 0 inf inf inf inf inf inf inf infinf inf inf inf inf inf inf inf inf inf infinf inf inf 12 8.8 inf inf inf inf ;inf inf inf inf inf inf inf inf inf inf infinf inf inf inf inf inf inf inf inf inf infinf inf inf 0 7.8 inf inf inf inf inf infinf inf inf inf inf inf inf inf inf inf infinf inf inf inf 10.5 inf 10.5 infinf ;inf inf inf inf inf inf inf inf inf inf infinf inf inf inf inf inf inf inf inf inf infinf 18.8 inf 7.8 0 7.9 inf inf inf infinf inf inf inf inf inf inf inf inf inf infinf inf inf inf inf inf inf inf inf inf ;inf inf inf inf inf inf inf inf inf inf infinf inf inf inf inf inf inf inf inf inf infinf inf inf inf 7.9 0 inf inf inf inf infinf inf inf inf inf inf inf inf inf inf infinf inf inf inf inf inf 12.1 8.3 inf ;inf inf inf inf inf inf inf inf inf inf infinf inf inf inf inf inf inf inf inf inf infinf inf inf inf inf inf 0 inf inf inf infinf inf inf inf inf inf inf inf inf inf infinf inf inf inf inf inf 15.2 7.2 7.8 ;inf inf inf inf inf inf inf inf inf inf infinf inf inf inf inf inf inf inf inf inf infinf inf inf inf inf inf inf 0 inf inf 10.3 inf inf inf inf inf inf inf inf inf inf infinf inf inf inf inf inf inf 7.7 inf ;inf inf inf inf inf inf inf inf inf inf infinf inf inf inf inf inf inf inf inf inf infinf inf inf inf inf inf inf inf 0 8.1 7.3inf inf inf inf inf inf inf inf inf inf infinf inf inf inf inf inf inf inf 9.2 ;inf inf inf inf inf inf inf inf inf inf infinf inf inf inf inf inf inf inf inf inf infinf inf inf inf inf inf inf inf 8.1 0 19 inf 14.9 inf inf inf inf inf inf inf infinf inf inf inf inf inf inf inf inf inf ;inf inf inf inf inf inf inf inf inf inf infinf inf inf inf inf inf inf inf inf inf infinf inf inf inf inf inf inf 10.3 7.3 190 inf inf 7.4 inf inf inf inf inf inf infinf inf inf inf inf inf inf inf inf inf ;inf inf inf inf inf inf inf inf inf inf infinf inf inf inf inf inf inf inf inf inf infinf inf inf inf inf inf inf inf inf inf inf0 8.2 11.5 17.8 inf inf inf inf infinf inf inf inf inf inf inf inf inf inf inf ;inf inf inf inf inf inf inf inf inf inf infinf inf inf inf inf inf inf inf inf inf infinf inf inf inf inf inf inf inf inf 14.9 inf 8.2 0 inf inf inf inf inf inf inf infinf inf inf inf inf inf inf inf inf inf ;10.3 inf inf inf inf inf inf inf inf infinf inf inf inf inf inf inf inf inf inf infinf inf inf inf inf inf inf inf inf inf inf7.4 11.5 inf 0 inf inf inf inf inf infinf inf inf inf inf inf inf inf inf inf 8.8 ;5.9 inf inf inf inf inf inf inf inf inf infinf inf inf inf inf inf inf inf inf inf infinf inf inf inf inf inf inf inf inf inf inf 17.8 inf inf 0 11 inf inf inf inf infinf inf inf inf inf inf inf inf inf inf ;11.2 inf 7.8 inf inf inf inf inf inf infinf inf inf inf inf inf inf inf inf inf infinf inf inf inf inf inf inf inf inf inf infinf inf inf inf 11 0 inf inf inf inf infinf inf inf inf inf inf 11.5 inf inf inf ;inf inf 8.2 12.7 11.3 inf 15.1 infinf inf inf inf inf inf inf inf inf inf infinf inf inf inf inf inf inf inf inf inf infinf inf inf inf inf inf inf inf 0 inf infinf inf inf inf inf inf inf inf inf inf infinf ;inf inf inf inf inf inf 7.2 8 7.8 inf 14.2 inf inf inf inf inf inf inf inf inf inf infinf inf inf inf inf inf inf inf inf inf infinf inf inf inf inf inf 0 inf inf inf infinf inf inf inf inf inf inf inf inf ;inf inf inf inf inf inf inf inf 5.6 10.8 inf 12.2 inf inf inf inf inf inf inf inf inf inf inf inf inf inf inf inf inf inf infinf inf inf inf inf inf inf inf inf 0 infinf inf inf inf inf inf inf inf inf inf inf ;inf inf inf inf inf inf inf inf inf inf 6.87.8 8.8 inf inf inf inf inf inf inf inf infinf inf inf inf inf inf inf inf inf inf infinf inf inf inf inf inf inf inf 0 inf infinf inf inf inf inf inf inf inf inf ;inf inf inf inf inf inf inf inf inf inf inf 10.2 inf 9.9 inf inf inf inf inf inf infinf inf inf inf inf inf inf inf inf inf infinf inf inf inf inf inf inf inf inf inf 0 inf inf inf inf inf inf inf inf inf inf ;inf inf inf inf inf inf inf inf inf inf infinf 16.4 inf inf 11.8 inf 8.2 inf infinf inf inf inf inf inf inf inf inf inf infinf inf inf inf inf inf inf inf inf inf infinf 0 inf inf inf inf inf inf inf inf inf ;inf inf inf inf inf inf inf inf inf inf 13.2 inf 9.8 inf inf inf inf 8.2 8.1 inf inf infinf inf inf inf inf inf inf inf inf inf infinf inf inf inf inf inf inf inf inf inf inf0 inf inf inf inf inf inf inf inf ;inf inf inf inf inf inf inf inf inf inf infinf inf inf inf inf 9.8 9.2 inf inf 4.1 10.1 inf inf inf inf inf inf inf inf inf inf infinf inf inf inf inf inf inf inf inf inf infinf 0 inf inf inf inf inf inf inf ;inf inf inf inf inf 11.8 14.5 inf infinf inf inf inf inf 8.8 inf inf inf 7.2 5.5inf inf inf inf inf inf inf inf inf inf infinf inf inf inf inf inf inf inf inf inf infinf inf inf inf 0 inf inf inf inf inf inf ;inf inf inf inf 11.4 9.5 inf inf inf infinf inf inf inf inf inf inf inf inf inf infinf inf inf 12 inf inf inf inf inf inf infinf inf inf inf inf inf inf inf inf inf infinf inf inf inf 0 14.2 19.8 inf infinf ;inf inf inf inf inf inf inf inf inf inf infinf inf inf inf inf inf inf inf inf inf inf7.9 13.2 8.8 10.5 inf inf inf inf infinf inf inf inf inf inf inf inf inf inf infinf inf inf inf inf 14.2 0 inf inf infinf ;6 8.2 inf inf inf inf inf inf inf inf inf inf inf inf inf inf inf inf inf inf inf inf inf inf inf inf inf inf inf inf inf inf inf inf inf inf inf 11.5 inf inf inf inf inf inf inf inf inf 19.8 inf 0 10.1 inf 12.8 ;inf inf inf inf inf inf inf inf inf inf inf inf inf inf inf inf inf inf inf inf inf inf inf inf inf 10.5 inf 12.1 15.2 inf inf inf inf inf inf inf inf inf inf inf inf inf inf inf inf inf inf inf inf 10.1 0 inf inf ;inf inf inf inf inf inf inf inf inf inf inf inf inf inf inf inf inf inf inf inf inf inf inf inf inf inf inf 8.3 7.2 7.7 inf inf inf inf inf inf inf inf inf inf inf inf inf inf inf inf inf inf inf inf inf 0 inf ;inf inf inf inf inf inf inf inf inf inf inf inf inf inf inf inf inf inf inf inf inf inf inf inf inf inf inf inf 7.8 inf 9.2 inf inf inf inf 8.8 inf inf inf inf inf inf inf inf inf inf inf inf inf 12.8 inf inf 0 ;];n=53;%有53个点k=1;for i=1:n-1for j=i+1:nif w(i,j)~=infx(1,k)=w(i,j);%记录边x(2,k)=i;%记录起点x(3,k)=j;%记录终点k=k+1;endendendk=k-1;%统计边数 k为边数%步骤一%冒泡法给边的大小排序for i=1:kfor j=i+1:kif x(1,i)>x(1,j)a=x(1,i);x(1,i)=x(1,j);x(1,j)=a;a=x(2,i);x(2,i)=x(2,j);x(2,j)=a;a=x(3,i);x(3,i)=x(3,j);x(3,j)=a;endendend%给各点标号赋初值for i=1:nl(i)=i;end%初始时选e1加入集合EE(1,1)=x(1,1); %E矩阵的第一行记录最小生成树的边长E(2,1)=x(2,1); %E矩阵的第二行记录边的起点E(3,1)=x(3,1); %E矩阵的第三行记录边的终点a=min([l(E(2,1)),l(E(3,1))]);l(E(2,1))=a;l(E(3,1))=a;b=1;%记录E中边数for i=2:k%步骤四if b==n-1 %如果树中边数达到n-1break%算法终止end%步骤二if l(x(2,i))~=l(x(3,i)) %如果两顶点标号不同b=b+1; %将这条边加入EE(1,b)=x(1,i);E(2,b)=x(2,i);E(3,b)=x(3,i);%步骤三for j=1:n %对于所有顶点if l(j)==max([l(E(2,b)),l(E(3,b))])%如果该顶点的标号,等于=,新加入边中的顶点标号较大的值l(j)=min([l(E(2,b)),l(E(3,b))]);%将其改为较小的那一个以避圈endendendendE附录二：问题一的求解程序1、计算强加权矩阵程序%floyd 算法通用程序，输入a为赋权邻接矩阵%输出为距离矩阵D，和最短路径矩阵pathfunction [D,path]=floyd(a)a=[0 inf inf inf inf inf inf inf inf inf inf inf inf 10.3 5.9 inf 6 inf inf inf ; inf 0 8.9 inf inf inf inf inf inf inf inf inf inf inf inf 7.9 inf inf inf inf ;inf 8.9 0 inf 18.8 inf inf inf inf inf inf inf inf inf inf 13.2 inf inf inf inf ; inf inf inf 0 7.8 inf inf inf inf inf inf inf inf inf inf 10.5 inf 10.5 inf inf ;inf inf 18.8 7.8 0 7.9 inf inf inf inf inf inf inf inf inf inf inf inf inf inf ;inf inf inf inf 7.9 0 inf inf inf inf infinf inf inf inf inf inf 12.1 8.3 inf ;inf inf inf inf inf inf 0 inf inf inf infinf inf inf inf inf inf 15.2 7.2 7.8 ;inf inf inf inf inf inf inf 0 inf 10.3 inf inf inf inf inf inf inf inf 7.7 inf ;inf inf inf inf inf inf inf inf 0 8.1 7.3inf inf inf inf inf inf inf inf 9.2 ;inf inf inf inf inf inf inf 10.3 8.1 0 19 inf 14.9 inf inf inf inf inf inf inf ;inf inf inf inf inf inf inf inf 7.3 19 0inf 20.3 7.4 inf inf inf inf inf inf ;inf inf inf inf inf inf inf inf inf inf inf0 8.2 11.5 17.8 inf inf inf infinf ;inf inf inf inf inf inf inf inf inf 14.9 20.3 8.2 0 inf inf inf inf inf inf inf ; 10.3 inf inf inf inf inf inf inf inf inf7.4 11.5 inf 0 inf inf inf inf inf 8.8 ;5.9 inf inf inf inf inf inf inf inf inf inf 17.8 inf inf 0 inf inf inf inf inf ;inf 7.9 13.2 10.5 inf inf inf inf inf inf inf inf inf inf inf 0 inf inf inf inf ;6 inf inf inf inf inf inf inf inf inf inf inf inf inf inf inf 0 10.1 inf 12.8 ;inf inf inf 10.5 inf 12.1 15.2 inf inf inf inf inf inf inf inf inf 10.1 0 inf inf ;inf inf inf inf inf 8.3 7.2 7.7 inf inf inf inf inf inf inf inf inf inf 0 inf ;inf inf inf inf inf inf 7.8 inf 9.2 inf inf inf inf 8.8 inf inf 12.8 inf inf 0 ;];n=size(a,1);D=a;path=zeros(n,n);for i=1:nfor j=1:nif D(i,j)~=infpath(i,j)=j;endendendfor k=1:nfor i=1:nfor j=1:nif D(i,k)+D(k,j)<D(i,j)D(i,j)=D(i,k)+D(k,j);path(i,j)=path(i,k);endendendend2、第1组巡视最短路线程序（第2，3组只变换数据）。

行遍性问题

定义在加权图G=(V,E)中，（１）权最小的哈密尔顿圈称为最佳圈．最佳H圈最佳（２）经过每个顶点至少一次的权最小的闭通路称为最最佳推销员回路．佳推销员回路一般说来，最佳哈密尔顿圈不一定是最佳推销员回路，同样最佳推销员回路也不一定是最佳哈密尔顿圈．
H回路，长22
最佳推销员回路，长4
算法步骤：算法步骤：
（１）用 Floyd 算法求出的所有奇次顶点之间的最短路径和距离．
（２）以 G 的所有奇次顶点为顶点集（个数为偶数），作一完备图，边上的权为两端点在原图 G 中的最短距离，将此完备加权图记为 G1．
（３）用Edmonds算法求出G1的最小权理想匹配最小权理想匹配M，得到奇次顶点的最小权理想匹配最佳配对．
返回
（二）推销员问题
流动推销员需要访问某地区的所有城镇，最后回到出发点．问如何安排旅行路线使总行程最小．这就是推销推销员问题．员问题若用顶点表示城镇，边表示连接两城镇的路，边上的权表示距离（或时间、费用），于是推销员问题就成为在加权图中寻找一条经过每个顶点至少一次的最短闭通路问题．
返回
二、推销员问题（一）哈密尔顿图
定义设G=(V,E)是连通无向图１２３经过G的每个顶点正好一次的路径，称为G的一条哈密尔顿路径哈密尔顿路径．哈密尔顿路径经过G的每个顶点正好一次的圈，称为G的哈密尔顿圈哈密尔顿圈或H圈．哈密尔顿圈含H圈的图称为哈密尔顿图哈密尔顿图或H图．哈密尔顿图图
用 Floyd 算法求出ቤተ መጻሕፍቲ ባይዱ们之间的最短路径和距离：
2．以 v4、v7、v8、v9 为顶点，它们之间的距离为边权构造完备图 G1．
3．求出 G1 的最小权完美匹配 M={(v4,,v7),(v8,v9)}

1998年全国大学生数学建模竞赛题之欧阳术创编

1998年全国大学生数学建模竞赛题目B题灾情巡视路线下图为某县的乡（镇）、村公路网示意图，公路边的数字为该路段的公里数。

今年夏天该县遭受水灾。

为考察灾情、组织自救，县领导决定，带领有关部门负责人到全县各乡（镇）、村巡视。

巡视路线指从县政府所在地出发，走遍各乡（镇）、村，又回到县政府所在地的路线。

(1) 若分三组（路）巡视，试设计总路程最短且各组尽可能均衡的巡视路线。

(2) 假定巡视人员在各乡（镇）停留时间T=2小时，在各村停留时间t=1小时，汽车行驶速度V=35公里/小时。

要在24小时内完成巡视，至少应分几组；给出这种分组下你认为最佳的巡视路线。

(3) 在上述关于T , t和V的假定下，如果巡视人员足够多，完成巡视的最短时间是多少；给出在这种最短时间完成巡视的要求下，你认为最佳的巡视路线。

(4) 若巡视组数已定(如三组），要求尽快完成巡视，讨论T，t和V改变对最佳巡视路线的影响。

灾情巡视路线模型摘要本文将求最佳巡视路线间题转化为图论中求最佳推销员回路（哈米尔顿回路）的问题,并用近似算法去寻求近似最优解。

对赋权图中的路径分组问题定义了均衡度用以衡量分组的均衡性。

对问题1，运用求任意两点间最短路的Floyd 算法,得出总路程较短且各组尽可能均衡的路线,各组的巡视路程分别为216.4公里,191.1公里,192.3公里,总路程599.8公里。

对问题2,证明了应至少分为4组,并求出了分为4组时各组的较优巡视路线,各组的巡视时间分别为22.74小时,22.59小时,21.69小时,22.54小时。

对问题3,求出完成巡视的最短时间为6.43小时,并用较为合理的分组的准则,分成22个组对问题4，研究了在不影响分组的均衡条件下, T,t,V 的允许变化范围,并得出了这三个变量的关系式,并由此对分三个组的情况进行了具体讨论。

1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

图中寻找从给定点O出发，行遍所有顶点至少一次
再回到点O，使得总权（路程或时间）最小.
A
4
本题是旅行售货员问题的延伸－多旅行售货员问题.
本题所求的分组巡视的最佳路线，也就是m条
经过同一点并覆盖所有其他顶点又使边权之和达到
最小的闭链（闭迹）. 如第一问是三个旅行售货员问题，第二问是四
个旅行售货员问题. 众所周知，旅行售货员问题属于NP完全问题，
4) 随机搜索出G中若干个H圈，例如2000个；
5) 对第2)，3)，4)步所得的每个H圈，用二边逐次修正法进行优化，得到近似最优H圈；
6) 在第5)步求出的所有H圈中，找出权最小的一个,
此即要找的最优H圈的A 近似解.
7
问题一若分为三组巡视，设计总路程最短且各
组尽可能均衡的巡视路线.
此问题是多个售货员的最佳旅行售货员问题.
i
子图G[Vi ]中的最佳旅行售货员回路，(Ci )为
Ci
的权，i,
n
j
1,2,3,..., n.
4) (Ci) min
i1
A
8
max | (Ci ) (C j ) |
定义称0 i, j max (Ci )
为该分组的实际
i
均衡度. 为最大容许均衡度.
显然0 0 1，0越小，说明分组的均衡性越
从O点出发去其它点，要使路程较小应尽量走 O点到该点的最短路.
故用软件包求出O点到其余顶点的最短路. 这些最短路构成一棵O为树根的树. 将从O点出发的树枝称为干枝.
A
10
准在则由分1 上尽组述量时分使应组同遵准一从则干准，枝则我上：们及找其到分两枝种上分的组点形分式在如同下一：组. 准分则从组2O1点应:（出将⑥发相，到邻①其的）它干，点枝（共上②有的，6点条③分干）在枝，同，（一它⑤组们，；的④名）称分准分别则组为32尽①:（量，①将②，长，②的③）干，，枝④（与，③短⑤，的，④干⑥）枝. ，分（在⑤同，一⑥组）.
A
6
近证第因似最能2二)算佳得，边法旅到3逐)求行，较次其售4优修)一货步的正个员分计法近问别算的似题用结结最是三果果优N种. 与P解方—初，法完始来产全圈代生问有替初题关最始,,采故优圈用本解，一算.以种法保
算法一求加权图的最佳旅行售货员回路近似算法:
1) 用图论软件包求出G中任意两个顶点间的最短路, 构造出完全图 G ( V , E ) ( x , , y ) E ,( x , y ) mdiG (n x,y); 2) 输入图 G 的一个初始H圈； 3) 用对角线完全算法（见[23]）产生一个初始圈;
长度总长度
O—P—28—27—26—N—24—23—22—17—16—I—15— I—18—K—21—20—25—M—O O—2—5—6—L—19—J—11—G—13—14—H—12—F— 10—F—9—E—7—E— 8—4—D—3—C—O O—R—29—Q—30—32—31—33—35—34—A—B—1—O
分组1极不均衡,故考虑分组2.
A
11
分组2:(①,②),(③,④),(⑤,⑥)
对分组2中每组顶点的生成子图,用算法一求出近似最优解及相应的巡视路线.
在每个子图所构造的完全图中,取一个尽量包含上
图中树上的边的H圈作为其第2)步输入的初始圈.
A
12
分组2的近似解
小组名称
I II
III
路
线
总路线路线的
好. 取定一个后，0与满足条件 3）的分组是
一个均衡分组. 条件 4）表示总巡视路线最短.
此问题包含两方面：a)对顶点分组, b)在每组中
求(单个售货员)最佳旅行售货员回路.
因单个售货员的最佳旅行售货员回路问题不存
故多
也不
存在多项式时间内的精确算法.
A
9
而图中节点数较多，为53个，我们只能去寻求一种较合理的划分准则，对图1进行粗步划分后,求出各部分的近似最佳旅行售货员回路的权,再进一进一步进行调整，使得各部分满足均衡性条件3).
A
191.1
241.9 125.5
558.5 13
因为该分组的均衡度
0(m C 1) a (C x (C i)2)24.2 9 14.1 912.55 54.2%
.
i1,2,3
所以此分法的均衡性很差.
为改善均衡性，将第Ⅱ组中的顶点C,2,3,D,4
分给第Ⅲ组（顶点2为这两组的公共点），重新分
本题给出了某县的公路网络图，要求的是在不
同的条件下，灾情巡视的最佳分组方案和路线.
将每个乡（镇）或村看作一个图的顶点，各乡镇、村之间的公路看作此图对应顶点间的边，各条
公路的长度（或行驶时间）看作对应边上的权，所
给公路网就转化为加权网络图，问题就转化图论中一类称之为旅行售货员问题，即在给定的加权网络
1. 问题引入与分析
1) 98年全国大学生数学建模竞赛B题“最佳灾情巡视路线”中的前两个问题是这样的：
今年(1998年)夏天某县遭受水灾. 为考察灾情、
组织自救，县领导决定，带领有关部门负责人到全县各乡（镇）、村巡视. 巡视路线指从县政府所在地出发，走遍各乡（镇）、村，又回到县政府所在地的路线.
即求解没有多项式时间算法. 显然本问题更应属于NP完全问题. 有鉴于此，
一定要针对问题的实际特点寻找简便方法，想找到
解决此类问题的一般方法是不现实的，对于规模较大
的问题可使用近似算法来求A 得近似最优解.
5
6. 最佳灾情巡视路线的模型的建
立与求解
问题转化为在给定的加权网络图中寻找从
给定点O出发, 行遍所有顶点至少一次再回回到点O ,使得总权(路程或时时间)最小,即最佳旅行售货员问题.
A
1
1）若分三组（路）巡视，试设计总路程最短且各组尽可能均衡的巡视路线.
2）假定巡视人员在各乡（镇）停留时间T=2 小时，在各村停留时间t=1小时，汽车行驶速度V =35公里/小时. 要在24小时内完成巡视，至少应分几组；给出这种分组下最佳的巡视路线.
A
2
公路边的数字为该路段的公里数.
Hale Waihona Puke A32) 问题分析：
即在加权图G中求顶点集V 的划分V1,V2, ,Vn，将G
分成 n 个生成子图G[V1], G[V2 ],
,
G[Vn
]，使得
n
1) 顶点O Vi, i 1,2,3, ,n. 2) Vi V (G).
max | (Ci ) (C j ) |
i1
3) i, j
max (Ci )
，其中Ci 为Vi的导出

案例：最佳灾情巡视路线

合集下载

图论1

1998年全国大学生数学建模竞赛题

灾情巡视路线

1998年全国大学生数学建模竞赛题

最佳灾情巡视路线模型

数模论文之灾情巡视路线

问题引入与分析

灾情巡视的数学模型

1998年全国大学生数学建模竞赛题之欧阳科创编

旅行商问题(TSP)

灾区巡视--最佳路线-选择问题-数学建模

案例：最佳灾情巡视路线共22页

灾情巡视路线的数学模型

1998年全国大学生数学建模竞赛题

灾情巡视路线程序

行遍性问题

1998年全国大学生数学建模竞赛题之欧阳术创编

文档推荐

最新文档