C语言-三维图形变换

C语言的三维数组的应用摘要：利用程序语言【C语言】编写一个俄罗斯方块游戏，加深对程序入口、出口的理解和编制，掌握数组的运用，以及对知识的拓展。

关键字：C语言, 俄罗斯方块, 三维数组Abstract: [C programming language - language prepared by a Russian box game, understand the procedures for import, export of understanding and preparation, master the use of the array, and the expansion of knowledge.Keyword: C language, the Russian box,three-dimensional array前言：本设计是为了制作一个“俄罗斯方块”游戏。

俄罗斯方块是一款风靡全球的电视游戏机和掌上游戏机游戏，它曾经造成的轰动与造成的经济价值可以说是游戏史上的一件大事。

这款游戏最初是由苏联的游戏制作人Alex Pajitnov制作的，它看似简单但却变化无穷，令人上瘾。

相信大多数用户都还记得为它痴迷得茶不思饭不想的那个俄罗斯方块时代。

制作此软件是为了使用户既能感受到游戏中的乐趣，也给用户提供了一个展现自己高超技艺的场所。

在毕业论文选题上，我利用c语言制作俄罗斯方块游戏，在c语言中通过利用三维数组来存放最初的形状，利用四个方向键，来控制方块的移动和变形，利用ENTER,ESC,SPACE,HOME,来控制占停，退出，快速下落，和开始。

方块的形状，颜色都是随机的。

在游戏的旁边有积分，和下一个的形状，还设计了过关，加分等等。

系统进入游戏后，会出现俄罗斯方块的字样，和积分NUMBER,NEXTBOX。

按ESC退出游戏，结束出现 GAMEOVER，和成员名，通过函数实现各个功能。

目录一．概述1.1俄罗斯方块的题目的描述1.2俄罗斯方块的设计思想1.2.1详细规则、胜负判定方法1.2.2游戏操作方法1.3 开发工具1.4 软件运行环境1.5 项目任务书二、总体设计2.1 开发与设计的总体思想2.2 系统模块结构图2.3 模块设计2.3.1 主要模块2.3.2 图形修饰模块2.3.3 系统流程图2.3.4 按键及功能对照表2.3.5 主要函数名称以及功能表2.4 模块设计小结三、实验结果分析及程序代码四、结果分析：五、总结六、参考文献：一、概述：1.1俄罗斯方块的题目的描述1. 运行游戏时.界面随机的产生不同形状的方块,游戏者通过自己的操作使方块进行合理的堆积.如果每层达到饱和状态的时候会自动消除.然后游戏有规则的进行加分.分数达到一定的阶段.游戏的级别也会越来越高.然后方块下降的速度也会随之慢慢加快.以迎合游戏者的挑战,达到最加有趣的游戏!1.2俄罗斯方块的设计思想游戏是用来给大家娱乐的，所以要能在使用的过程中给大家带来快乐，消除大家的疲劳，所以我们在游戏中添加了漂亮的场景和动听的音乐，设置了过关升级的功能，激发大家的娱乐激情。

题目：探索C++中的Matrix3D用法与应用序言C++是一种广泛应用于软件开发领域的编程语言，其强大的性能和灵活性使得它成为了许多领域的首选语言之一。

而在C++中，Matrix3D 作为一个重要的数据结构，在许多领域中都有着广泛的应用。

本文将深入探讨C++中Matrix3D的相关知识，从基础的概念到高级应用，帮助读者全面理解其用法与应用。

一、Matrix3D的基本概念在C++中，Matrix3D是一个三维的矩阵结构，它由行和列组成，用于表示三维空间中的变换和旋转。

Matrix3D中的元素可以表示空间中的平移、旋转、缩放等变换，是实现三维图形学和计算机视觉算法的重要基础。

了解Matrix3D的基本概念对于掌握C++中的三维编程至关重要。

二、Matrix3D的创建和初始化在C++中，我们可以使用数组或动态内存分配的方式来创建和初始化Matrix3D。

通过合适的初始化，我们可以为Matrix3D赋予特定的数学含义和几何意义，从而实现不同的空间变换和仿射变换。

在实际应用中，不同的初始化方法往往对应着不同的数学模型和算法，因此选择适合的初始化方法对于实现特定的功能非常重要。

三、Matrix3D的操作和运算Matrix3D作为一个矩阵结构，支持多种基本的矩阵运算，如加法、减法、乘法等。

这些运算不仅可以用来表示空间变换，还可以应用于解决实际问题，比如三维图形的变换和投影、物体的运动和碰撞检测等。

在实际编程中，熟练掌握Matrix3D的操作和运算对于提高代码的效率和性能至关重要。

四、Matrix3D在计算机图形学中的应用在计算机图形学中，Matrix3D有着广泛的应用。

它可以用来表示三维空间中的几何变换、物体的旋转和平移、相机的视角和投影等。

通过Matrix3D的变换，我们可以实现三维场景的渲染和显示，从而为用户呈现逼真的三维图形效果。

在实际开发中，熟练掌握Matrix3D在计算机图形学中的应用对于实现高质量的三维图形效果至关重要。

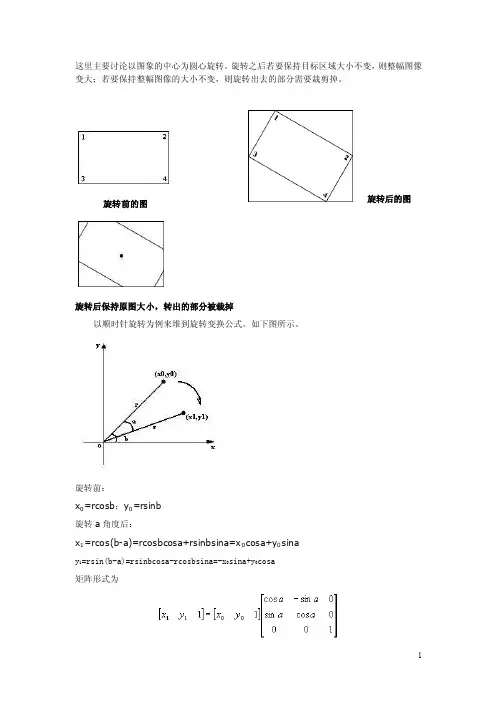
这里主要讨论以图象的中心为圆心旋转。

旋转之后若要保持目标区域大小不变，则整幅图像变大；若要保持整幅图像的大小不变，则旋转出去的部分需要裁剪掉。

旋转前的图旋转后的图旋转后保持原图大小，转出的部分被裁掉以顺时针旋转为例来堆到旋转变换公式。

如下图所示。

旋转前：x0=rcosb；y0=rsinb旋转a角度后：x1=rcos(b-a)=rcosbcosa+rsinbsina=x0cosa+y0sinay 1=rsin(b-a)=rsinbcosa-rcosbsina=-xsina+ycosa矩阵形式为逆变换为上面的公式是以图像的左下角为原点旋转的。

现我们要以图像的中心为原点旋转。

因此需要先将坐标平移到图像中心，如下所示设图象的宽为w，高为h，容易得到：逆变换为现在可以分三步来完成旋转变换：1. 将坐标系x'o'y'平移到xoy ；2. 在xoy坐标系下作旋转变换；3.变换后将坐标系平移回原来位置。

用矩阵表示就是其中R表示旋转变换矩阵。

当旋转不改变图像大小时，T 与T' 互为逆矩阵；当旋转后图像变大时，T 与T'不是逆矩阵关系，因为图像变大了，第一次平移和第二次平移坐标系的距离不一样。

因此当图像变大时，公式应该如下：由于算法实现过程中我们需要的是逆变换的公式，因此我们只写出逆变换的表达式，如下：其中wn ,hn 表示新图像的宽和高，wo, ho 表示原图像的宽和高。

这样，对于新图中的每一点，我们就可以根据上面逆变换公式求出对应原图中的点，得到它的灰度。

如果超出原图范围，则设置为背景色。

要注意的是，由于有浮点运算，计算出来点的坐标可能不是整数，采用取整处理，即找最接近的点，这样会带来一些误差(图象可能会出现锯齿)。

更精确的方法是采用插值，这里暂不讨论。

C++代码如下：/** rotate.cpp* 图像旋转变换(顺时针)* Created on: 2011-10-10* Author: LiChanghai*/// 以图像中心为坐标原点，旋转后不改变图像大小// 函数返回值为指针，指向新申请的内存区域// 因为新图像大小改变了，需要返回新图像的尺寸// 因此形参的高度和宽度都采用指针变量#include<string.h>#include<stdlib.h>#include<cmath>#define pi 3.1415926535unsigned char* rotate(unsigned char*pImage, int*width, int*height, int biBitCount, float angle){//定义以图像中心为原点的坐标系下原图像和新图像的四个角点坐标float src_x1, src_y1, src_x2, src_y2, src_x3, src_y3, src_x4, src_y4;float dst_x1, dst_y1, dst_x2, dst_y2, dst_x3, dst_y3, dst_x4, dst_y4;//定义新图像的高度和宽度int wnew, hnew;//定义计算过程中需要的相关变量float sina, cosa, temp1, temp2, alpha;//角度转化为弧度alpha=pi*angle/180;cosa = float(cos(double(alpha)));sina = float(sin(double(alpha)));//原图像的四个角点的坐标src_x1 = float(-0.5*(*width)); src_y1 = float(0.5*(*height));src_x2 = float(0.5*(*width)); src_y2 = src_y1;src_x3 = src_x1; src_y3 = float(-0.5*(*height));src_x4 = src_x2; src_y4 = src_y3;//计算新图像的四个角点坐标dst_x1 = cosa*src_x1+sina*src_y1;dst_y1 = -sina*src_x1+cosa*src_y1;dst_x2 = cosa*src_x2+sina*src_y2;dst_y2 = -sina*src_x2+cosa*src_y2;dst_x3 = cosa*src_x3+sina*src_y3;dst_y3 = -sina*src_x3+cosa*src_y3;dst_x4 = cosa*src_x4+sina*src_y4;dst_y4 = -sina*src_x4+cosa*src_y4;//计算新图像的高度和宽度float t1 = fabs(dst_x4-dst_x1), t2 = fabs(dst_x3-dst_x2);wnew = int(t1>t2 ? t1:t2);t1 = fabs(dst_y4-dst_y1), t2 = fabs(dst_y3-dst_y2);hnew = int(t1>t2 ? t1:t2);// 计算旋转变换中的两个中间变量，便于以后计算temp1=float( -0.5*wnew*cosa+0.5*hnew*sina+0.5*(*width));temp2=float(-0.5*wnew*sina-0.5*hnew*cosa+0.5*(*height));//计算原图像和新图像每行像素所占的字节数（必须是4的倍数）int lineByte = ((*width) * biBitCount/8+3)/4*4;int lineByte2=(wnew * biBitCount/8+3)/4*4;//申请新的位图数据存储空间unsigned char*pImage2;pImage2=new unsigned char[lineByte2*hnew];//将新图像设置为背景色memset(pImage2, 0, lineByte2*hnew);//遍历新图像的每一个像素进行判断int x, y, x0, y0; // x0, y0为原图像中对应坐标for(y=0; y<hnew; y++)for(x=0; x<wnew; x++){x0= int(x*cosa-y*sina+temp1);y0= int(x*sina+y*cosa+temp2);//如果在原图像范围内则复制像素值if( (x0>=0) && (x0<(*width)) && (y0>=0) && (y0<(*height))){*(pImage2+lineByte2*y+x) = *(pImage+lineByte*y0+x0);}}//修改原图像的高度和宽度*width = wnew;*height = hnew;delete [ ] pImage; //释放原内存空间return pImage2;}该程序在Eclipse上调试通过，结果正确。

三维投影变换的MATLAB实现唐飞;杨伟;查长礼【摘要】三维图形变换需要对形体顶点的齐次坐标矩阵进行复合计算,计算繁琐且变换过程晦涩抽象,使用传统的程序设计语言实现图形变换的可视化非常困难.因为在三维图形变换中引入MATLAB工具,利用其强大的矩阵运算能力和丰富的图形处理能力,能够快速准确地计算矩阵和输出图形,清晰直观地展现图形变换的方法和过程.【期刊名称】《安徽理工大学学报（自然科学版）》【年(卷),期】2016(036)002【总页数】4页(P36-39)【关键词】三维图形变换;矩阵;MATLAB;投影;计算机图形学【作者】唐飞;杨伟;查长礼【作者单位】安庆师范学院物理与电气工程学院,安徽安庆246133;安庆师范学院物理与电气工程学院,安徽安庆246133;安庆师范学院物理与电气工程学院,安徽安庆246133【正文语种】中文【中图分类】TH126.2几何图形是CAD系统中的基本元素，无论以何种方式建立的模型，最终都需要转换为几何图形进行显示和输出。

几何图形由顶点坐标、顶点间的拓扑关系和组成图形的线面模型共同决定[1]。

图形变换是计算机图形处理的基础，是计算机图形学的重要组成部分，图形的处理、显示和形体构造等都需要使用到图形变换。

图形变换的实质是对图形顶点的坐标进行变换，这种变换不改变图形各元素的属性和它们之间的拓扑关系，仅改变各点的坐标。

三维图形变换包括比例变换、对称变换、错切变换、平移变换、旋转变换、投影变换和透视变换等基本变换，更复杂的变换可以通过基本变换组合而成。

每一个变换都可以表示为矩阵计算的形式，通过矩阵的相乘构造更复杂的变换[2]。

在图形变换中需要进行大量的矩阵运算，计算繁琐且变换过程晦涩抽象，使用C语言等传统的计算机语言实现可视化程序设计十分困难。

因此在图形变换中使用MATLAB软件，利用其强大的矩阵运算能力和丰富的图形处理能力，快速准确地进行矩阵计算和图形输出，直观地展现图形变换的方法和过程。

三维坐标系变换三维坐标系变换可以理解为将一个三维点从一个坐标系转换到另一个坐标系中。

在实际应用中，我们常常需要对物体或者场景进行三维建模和渲染，而三维坐标系变换是不可或缺的一个基础环节。

本文将介绍三维坐标系变换的相关概念和常见应用，以及一些实用的解决方案。

一、常见的三维坐标系变换方式在三维坐标系变换中，常见的方式包括平移、旋转、缩放和仿射变换。

它们分别对应了三维空间中的平移、旋转、比例变化和直线间的关系变化。

在实际应用中，我们可以通过矩阵乘法的方式进行数学计算，也可以利用计算机图形学库中封装好的函数来实现。

1. 平移：将对象在三维坐标系中沿着某个方向移动一定的距离。

平移变换可以用一个形如平移向量的矩阵表示，在三维空间中的坐标变换表达式为：[x' y' z' 1] = [x y z 1] * [1 0 0 tx; 0 1 0 ty; 0 0 1 tz; 0 0 0 1]其中，tx、ty、tz 分别表示在 x、y、z 方向的平移距离。

2. 旋转：将对象绕三维空间中的某个坐标轴或者任意轴进行旋转变换。

如果绕 x 轴旋转，那么旋转变换矩阵为：[x' y' z' 1] = [x y z 1] * [1 0 0 0; 0 cos(theta) -sin(theta) 0; 0 sin(theta) cos(theta) 0; 0 0 0 1]同样的，绕 y 轴、z 轴旋转的矩阵也可以类似地表示。

对于绕任一轴的旋转，可以使用 Rodrigues 公式等数学方法来求解。

3. 缩放：将对象在三个方向上分别进行缩放变换，可以分别用三个缩放因子表示，对应矩阵表示为：[x' y' z' 1] = [x y z 1] * [sx 0 0 0; 0 sy 0 0; 0 0 sz 0; 0 0 0 1]其中，sx、sy、sz 分别表示在 x、y、z 方向放缩的比例因子。

实验报告模板《计算机图形学》实验报告一、实验目的及要求1．实习三维图形的坐标系之间的变换；2．三维图形几何变换；3．掌握三维图形的坐标系之间的变换算法及三维图形几何变换的原理和实现；4．实现二维图形的基本变换（平移、旋转、缩放、错切、对称、复合等）；5．实现三维图形的基本变换（平移、旋转、缩放、复合等）；二、理论基础在齐次坐标理论下，二维图形几何变换矩阵可用下式表示：⎪⎪⎪⎭⎫⎝⎛===ifchebgdaTnkxx kk2,1,0,)(ϕ平移变换：[x* y* 1] =[x y 1] *0000001ts⎛⎫⎪⎪⎪⎝⎭=[t*x s*y 1]比例变换：[x* y* 1]=[x y 1] *1000101m n⎛⎫⎪⎪⎪⎝⎭=[m+x n+y 1]旋转变换：在平面上的二维图形饶原点逆时针旋转Ө角，变换矩阵为[x* y* 1]=[x y 1] *cos sin0sin cos0001θθθθ⎛⎫⎪- ⎪⎪⎝⎭= [x*cosө-y*sinө]复合变换：以上各种变换矩阵都是以原点为参照点，当以任意参照点进行变换的时候，我们就要用到复合变换矩阵。

三维变换类似于二维，在画图时，把三维坐标转换为二维即可。

三、算法设计与分析二维变换：#define dx 50#define dy 100void CCGWithVCView::OnTransScale() //平移（50,100）{// TODO: Add your command handler code here// AfxMessageBox(_T("Please Insert The Move Change Code!")) ;int m[4][2]={{100,50},{50,100},{150,100},{100,50}};int i;int a[2],b[2];CDC * pDC = GetDC();for(i=0;i<3;i++){a[0]=m[i][0];a[1]=m[i][1];b[0]=m[i+1][0];b[1]=m[i+1][1];DDALine(a,b, RGB(0, 200, 255), pDC);}for(i=0;i<3;i++){a[0]=m[i][0]+dx;a[1]=m[i][1]+dy;b[0]=m[i+1][0]+dx;b[1]=m[i+1][1]+dy;DDALine(a,b, RGB(0, 200, 255), pDC);}}#define h 0.1745#include<math.h>void CCGWithVCView::OnTransRotate() //旋转{// TODO: Add your command handler code here// AfxMessageBox(_T("Please Insert The Rotate Change Code!")) ;int m[4][2]={{100,50},{50,100},{150,100},{100,50}};int i;int a[2],b[2];CDC * pDC = GetDC();for(i=0;i<3;i++){a[0]=m[i][0];a[1]=m[i][1];b[0]=m[i+1][0];b[1]=m[i+1][1];DDALine(a,b, RGB(0, 200, 255), pDC);}for(i=0;i<3;i++){a[0]=m[i][0]*cos(h)-m[i][1]*sin(h);a[1]=m[i][1]*cos(h)+m[i][0]*sin(h);b[0]=m[i+1][0]*cos(h)-m[i+1][1]*sin(h);b[1]=m[i+1][1]*cos(h)+m[i+1][0]*sin(h);DDALine(a,b, RGB(0, 200, 255), pDC);}}#define k 2;#define f 2.5void CCGWithVCView::OnTransMove() //缩放{// TODO: Add your command handler code here//AfxMessageBox(_T("Please Insert The Scale Change Code!")) ;int m[4][2]={{100,50},{50,100},{150,100},{100,50}};int i;int a[2],b[2];CDC * pDC = GetDC();for(i=0;i<3;i++){a[0]=m[i][0];a[1]=m[i][1];b[0]=m[i+1][0];b[1]=m[i+1][1];DDALine(a,b, RGB(0, 200, 255), pDC);}for(i=0;i<3;i++){a[0]=m[i][0]*k;a[1]=m[i][1]*f;b[0]=m[i+1][0]*k;b[1]=m[i+1][1]*f;DDALine(a,b, RGB(0, 200, 255), pDC);}}#define n 2#define d 0void CCGWithVCView::OnTransOther(){// TODO: Add your command handler code here//AfxMessageBox(_T("Please Insert The Other Change Code!")) ;int m[4][2]={{100,50},{50,100},{150,100},{100,50}};int i;int a[2],b[2];CDC * pDC = GetDC();for(i=0;i<3;i++){a[0]=m[i][0];a[1]=m[i][1];b[0]=m[i+1][0];b[1]=m[i+1][1];DDALine(a,b, RGB(0, 200, 255), pDC);}for(i=0;i<3;i++){a[0]=m[i][0]+n*m[i][1];a[1]=m[i][1]+d*m[i][0];b[0]=m[i+1][0]+n*m[i+1][1];b[1]=m[i+1][1]+d*m[i+1][0];DDALine(a,b, RGB(0, 200, 255), pDC);}}三维变换：#include<math.h>#define dx 100#define dy 100#define dz 0void CCGWithVCView::OnTransScale() //平移（50,100）{// TODO: Add your command handler code here// AfxMessageBox(_T("Please Insert The Move Change Code!")) ;int i;int p2d[6][2];int p3d[6][3]={{400,300,0},{300,400,0},{300,300,10},{275,300,0},{400,300,0},{300,300,10}};for( i=0;i<6;i++){p2d[i][0]=p3d[i][1]-p3d[i][0]/sqrt(2);p2d[i][1]=p3d[i][2]+p3d[i][0]/sqrt(2);}int a[2],b[2];CDC * pDC = GetDC();for(i=0;i<5;i++){a[0]=p2d[i][0];a[1]=p2d[i][1];b[0]=p2d[i+1][0];b[1]=p2d[i+1][1];DDALine(a,b, RGB(0, 200, 255), pDC);}for( i=0;i<6;i++){p2d[i][0]=p3d[i][1]+dy-p3d[i][0]+dx/sqrt(2);p2d[i][1]=p3d[i][2]+dz+p3d[i][0]+dx/sqrt(2);}for(i=0;i<5;i++){a[0]=p2d[i][0];a[1]=p2d[i][1];b[0]=p2d[i+1][0];b[1]=p2d[i+1][1];DDALine(a,b, RGB(0, 0, 255), pDC);}}#define k 0.1745void CCGWithVCView::OnTransRotate() //旋转{// TODO: Add your command handler code here// AfxMessageBox(_T("Please Insert The Rotate Change Code!")) ;int i;int p2d[6][2];int p3d[6][3]={{400,300,0},{300,400,0},{300,300,10},{275,300,0},{400,300,0},{300,300,10}};for( i=0;i<6;i++){p2d[i][0]=p3d[i][1]-p3d[i][0]/sqrt(2);p2d[i][1]=p3d[i][2]+p3d[i][0]/sqrt(2);}int a[2],b[2];CDC * pDC = GetDC();for(i=0;i<5;i++){a[0]=p2d[i][0];a[1]=p2d[i][1];b[0]=p2d[i+1][0];b[1]=p2d[i+1][1];DDALine(a,b, RGB(0, 200, 255), pDC);}for( i=0;i<6;i++){p2d[i][0]=p3d[i][1]*cos(k)-p3d[i][2]*sin(k)-p3d[i][0]/sqrt(2);p2d[i][1]=p3d[i][2]*cos(k)+p3d[i][1]*sin(k)+p3d[i][0]/sqrt(2);}for(i=0;i<5;i++){a[0]=p2d[i][0];a[1]=p2d[i][1];b[0]=p2d[i+1][0];b[1]=p2d[i+1][1];DDALine(a,b, RGB(0, 0, 255), pDC);}}四、程序调试及结果的分析二维：三维：五、实验心得及建议在实验过程中，尽管过程中任由许多不会的地方，而且有待于今后的提高和改进，但我加深了对书本上知识的理解与掌握，同时也学到了很多书本上没有东西，并积累了一些宝贵的经验，这对我以后的学习与工作是不无裨益的。

实验三 3D图形变换一．实验目的：掌握3D图像的变换，了解多数的3D变换，平移，旋转等几何变换，还有投影变换等知识。

二．实验原理：3D图像的移动，比例变化，旋转等几何变换算法原理及各种投影变换算法原理。

三．实验步骤：一．建立MFC单文档程序，用来编写3D变换。

二．建立Mainframe，并设计，添加相应的ID及映射函数。

三．实验的主要代码：1、设计3维图形平移变换算法的实现程序；void CMyView::OnTranslation(){m_Select=SEL_TS;m_str="平移";CBaseClass my1; //构造新的CBaseClass对象int i,j;for ( i=1;i<=4;++i){for ( j=1;j<=4;++j)my1.A[i][j]=0;}my1.A[1][1]=1;my1.A[2][2]=1;my1.A[4][4]=1;my1.A[3][3]=1;my1.A[4][1]=20; //x轴方向上平移my1.A[4][2]=28; //y轴方向上平移my1.A[4][3]=28; //z轴方向上平移my1.Draw();}2、设计3维图形缩放变换算法的实现程序；void CMyView::OnScalingS(){m_Select=SEL_MO;m_str="整体变比";CBaseClass my1; //构造新的CBaseClass对象int i,j;for ( i=1;i<=4;++i){for ( j=1;j<=4;++j)my1.A[i][j]=0;}my1.A[1][1]=1;my1.A[2][2]=1;my1.A[3][3]=1;my1.A[4][4]=0.5;my1.Draw();}void CMyView::OnScalingXyz(){m_Select=SEL_MO;m_str="XYZ变比";CBaseClass my1; //构造新的CBaseClass对象int i,j;for ( i=1;i<=4;++i){for ( j=1;j<=4;++j)my1.A[i][j]=0;}my1.A[1][1]=2; //x轴方向上比例my1.A[2][2]=1; //y轴方向上比例my1.A[3][3]=2; //z轴方向上比例my1.A[4][4]=1;my1.Draw();}3、设计3维图形旋转变换算法的实现程序。

如何利用C语言进行图形化编程在计算机编程领域，图形化编程一直是一个备受关注的话题。

图形化编程可以使程序更加直观、易于理解，同时也能提升用户体验。

虽然C语言是一种被广泛应用的编程语言，但是它本身并不擅长处理图形化界面。

然而，我们可以通过一些技巧和工具来利用C语言进行图形化编程。

一、使用图形库在C语言中，我们可以使用图形库来实现图形化编程。

图形库是一种提供了绘制图形和处理图形界面的工具集。

其中，最常用的图形库是OpenGL和SDL。

OpenGL是一个跨平台的图形库，它可以在多个操作系统上运行，并且支持3D图形的绘制。

而SDL是一个简单易用的图形库，它专注于2D图形的绘制和处理。

通过使用这些图形库，我们可以在C语言中轻松实现图形化界面的编程。

二、学习GUI框架除了使用图形库，我们还可以学习和使用GUI（图形用户界面）框架来进行图形化编程。

GUI框架是一种提供了一系列图形化界面组件和工具的软件库。

在C 语言中，常用的GUI框架有GTK+和Qt。

GTK+是一个开源的GUI框架，它提供了一套丰富的界面组件和事件处理机制，可以用于创建跨平台的图形化应用程序。

而Qt是一个跨平台的GUI框架，它提供了一套完整的界面组件和工具，可以用于创建高度可定制的图形化应用程序。

通过学习和使用这些GUI框架，我们可以在C语言中实现复杂的图形化界面。

三、结合其他编程语言除了使用C语言本身的特性和工具，我们还可以结合其他编程语言来进行图形化编程。

例如，我们可以使用C语言与Python进行集成，利用Python的图形化编程库来实现图形化界面。

Python拥有丰富的图形化编程库，如Tkinter和PyQt，它们提供了一系列易用的界面组件和工具。

通过使用C语言与Python的结合，我们可以充分发挥C语言的计算性能，同时又能利用Python的图形化编程库来实现图形化界面。

四、自定义图形化库如果我们对现有的图形库和GUI框架不满意，我们还可以自己开发一个图形化库。

第六章 三维图形变换第一节 三维图形变换基础一、三维坐标系xyzxyz右手坐标系左手坐标系三维图形学中习惯上通常是采用右手坐标系。

xy 平面对应于视平面，z 轴垂直于视平面，指向视平面之外。

二、三维齐次坐标及变换矩阵三维图形变换也是基于矩阵运算进行。

矩阵运算的维数被扩展为四维。

三维坐标点采用4元齐次坐标表示：(x , y , z , 1)，三维坐标与三维齐次坐标的相互转换如下：三维坐标(x , y ,z )——齐次坐标(x , y ,z , 1) 齐次坐标(x , y ,z , h )——二维坐标(x /h , y /h ,z /h ) 变换矩阵则为4X4的矩阵：⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡s nm kr j i h q f e d p c b a 其中：平移变换第二节 三维几何变换一、三维基本变换 1. 平移变换⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡=1010000100001nmk T )1,,,()1,,,(n z m y k x T z y x +++=⋅2. 比例变换)1,,,()1,,,(1000000000000jz ey ax T z y x j e a T =⋅⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡= 3. 旋转变换三维的基本旋转变换分为三种，即绕三个坐标轴的旋转变换。

(1)绕z 轴旋转γ角旋转后z 值不变，x,y 值将发生改变，x,y 值的计算公式与平面旋转相同，即：zz y x y y x x ='+='-='γγγγcos sin sin cos 则变换矩阵为：⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡-=1000010000cos sin 00sin cos γγγγT 有：)1,1,cos sin ,sin cos ()1,,,(γγγγy x y x z y x +-=T(2)绕x 轴旋转α角则旋转后x 的坐标值不变，y 和z 的坐标值将改变，相当于在yz 平面上绕平面原点进行旋转变换。

平面转转变换的公式为：ααααcos sin sin cos y x y y x x +='-='对应而来，这里y 对应于x ，z 对应y ，有：ααααcos sin sin cos z y z z y y +='-='则变换矩阵为：⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡-=10000cos sin 00sin cos 00001ααααT )1,cos sin ,sin cos ,()1,,,(ααααz y z y x z y x +-=T(3)绕y 轴旋转β角这时，z 对应于x ，x 对应于y 。

c语言计算欧拉角+三轴在计算机图形学和机器人领域，欧拉角（Euler angles）和三轴（three-axis）旋转是常见的概念。

C语言作为一种强大的编程语言，可以用来实现欧拉角和三轴的计算。

本文将介绍如何使用C语言计算欧拉角和三轴的方法，并提供相应代码示例。

一、欧拉角的定义和计算欧拉角是用来表示物体在三维空间中的旋转姿态的一种方式。

它由三个角度组成，分别代表绕着三个坐标轴（通常是X、Y、Z轴）旋转的角度。

在C语言中，我们可以使用三个变量来表示欧拉角，分别存储X、Y、Z轴上的旋转角度。

然后，可以根据不同的旋转顺序，通过数学公式将欧拉角转换成旋转矩阵或四元数。

以下是一个示例代码，演示了如何计算欧拉角的旋转矩阵：```c#include <stdio.h>#include <math.h>typedef struct {double x;double y;double z;} EulerAngle;typedef struct {double m[3][3];} Matrix3x3;Matrix3x3 eulerToMatrix(EulerAngle euler) { Matrix3x3 mat;double sx = sin(euler.x);double cx = cos(euler.x);double sy = sin(euler.y);double cy = cos(euler.y);double sz = sin(euler.z);double cz = cos(euler.z);mat.m[0][0] = cy * cz;mat.m[0][1] = -cy * sz;mat.m[0][2] = sy;mat.m[1][0] = sx * sy * cz + cx * sz;mat.m[1][1] = -sx * sy * sz + cx * cz;mat.m[1][2] = -sx * cy;mat.m[2][0] = -cx * sy * cz + sx * sz;mat.m[2][1] = cx * sy * sz + sx * cz;mat.m[2][2] = cx * cy;return mat;}int main() {EulerAngle euler = {0.1, 0.2, 0.3};Matrix3x3 mat = eulerToMatrix(euler);printf("Rotation Matrix:\n");printf("%lf %lf %lf\n", mat.m[0][0], mat.m[0][1], mat.m[0][2]);printf("%lf %lf %lf\n", mat.m[1][0], mat.m[1][1], mat.m[1][2]);printf("%lf %lf %lf\n", mat.m[2][0], mat.m[2][1], mat.m[2][2]);return 0;}```以上代码实现了一个`eulerToMatrix`函数，该函数将欧拉角转换成旋转矩阵。

C语言在3D图形处理中的应用3D图形处理是现代计算机领域的一个重要应用方向，它广泛应用于电子游戏、影视特效、建筑设计和工业制造等领域。

C语言作为一种高效且功能强大的编程语言，被广泛应用于3D图形处理。

本文将介绍C语言在3D图形处理中的应用，并探讨其重要性和优势。

一、C语言在三维坐标系的表示三维图形的处理离不开三维坐标系的表示。

C语言提供了数据结构和算法来处理三维坐标系，并使得程序员能够方便地进行坐标系的运算和变换。

通过C语言提供的数据结构，开发人员可以轻松表示和操作三维场景中的各种物体。

二、C语言在3D模型的渲染中的应用渲染是指将3D场景中的物体绘制到屏幕上的过程。

C语言提供了强大的绘图功能，可以实现灯光效果、阴影效果、纹理贴图等，使得渲染出的图形更加逼真。

通过C语言编写的渲染算法，可以高效地处理大规模的三维场景。

三、C语言在3D图形变换中的应用图形变换是指对3D模型进行平移、旋转和缩放等操作。

C语言提供了矩阵计算和向量处理的功能，使得开发人员可以轻松实现各种图形变换。

通过矩阵计算和向量处理，可以将三维模型根据需求进行各种变换，实现动态效果和用户交互。

四、C语言在3D碰撞检测中的应用碰撞检测是指判断两个或多个三维模型是否发生碰撞的过程。

在许多实时应用中，如电子游戏和虚拟现实，快速而准确的碰撞检测是必要的。

C语言提供了高效的算法和数据结构，使得开发人员能够在实时场景中实现精确的碰撞检测。

五、C语言在3D图形优化中的应用在处理大规模三维场景时，性能优化成为一个关键问题。

C语言作为一种性能出色的编程语言，可以通过优化算法和数据结构来提升3D图形处理的效率。

通过使用合适的数据结构、优化算法和并行计算等技术，可以在3D图形处理中获得更高的性能。

六、结语C语言作为一种通用编程语言，在3D图形处理中发挥了重要作用。

它提供了丰富的算法和数据结构，使得开发人员能够优雅地实现各种图形处理操作。

通过灵活运用C语言的特性，可以创建出更加逼真、流畅的3D场景，并提供更好的用户体验。

四元数转换成欧拉角c语言四元数是一种数学结构，可以用来表示三维空间的旋转。

在计算机图形学和游戏开发中经常用到四元数来进行旋转的计算，但是有时需要将四元数转换成欧拉角（yaw、pitch、roll），以便更好地理解和使用。

本文将介绍如何在C语言中将四元数转换成欧拉角。

首先，需要了解四元数和欧拉角的定义和计算公式。

四元数可以表示为一个四元组(a, b, c, d)，其中a为实部，b, c, d为虚部，满足a^2 + b^2 + c^2 + d^2 = 1。

欧拉角则表示为三个角度yaw、pitch、roll，分别对应绕Z轴、Y轴、X轴旋转的角度。

四元数转换成欧拉角的步骤如下：1.计算yaw角度，即绕Z轴旋转的角度。

可以使用以下公式：yaw = atan2(2*(a*b+c*d),1-2*(b^2+c^2));2.计算pitch角度，即绕Y轴旋转的角度。

可以使用以下公式： sinp = 2*(a*c-d*b);if (abs(sinp) >= 1)pitch = copysign(M_PI/2, sinp);elsepitch = asin(sinp);3.计算roll角度，即绕X轴旋转的角度。

可以使用以下公式： roll = atan2(2*(a*d+b*c),1-2*(c^2+d^2));需要注意的是，这些公式中的函数和符号都需要在代码中正确地实现和使用。

此外，还需要考虑欧拉角的旋转顺序和坐标系的定义，以确保计算结果正确。

在实际应用中，还需要注意四元数的单位和符号，以及欧拉角的范围和精度等问题。

可以通过对四元数和欧拉角的理论和实践进行深入探讨和实验，来优化和完善算法和代码。