下载文档原格式
降阶法二阶微分方程组降阶法是求解二阶微分方程组的一种常用方法，用于将高阶微分方程组降阶为一阶方程组或二者的组合。
在此，我们将介绍如何用降阶法求解二阶微分方程组。
首先，考虑一个二阶微分方程组：$\begin{cases} x''(t) = f(t,x(t),x'(t)) \\ y''(t) = g(t,x(t),x'(t),y(t),y'(t)) \end{cases}$其中，$x(t)$和$y(t)$是未知函数，$f$和$g$是已知函数。
为了将方程组降阶，我们引入新的未知函数$v(t) = x'(t)$和$w(t) = y'(t)$。
然后，我们可以将原方程组转化为一阶方程组：$\begin{cases} v'(t) = f(t,x(t),v(t)) \\ w'(t) = g(t,x(t),v(t),y(t),w(t))\end{cases}$此时，我们需要求解一个四维的一阶微分方程组，而不是原来的二维二阶方程组。
接下来，我们需要使用初值条件来求解一阶方程组的解。
假设给定初始条件$x(t_0) = x_0$、$y(t_0) = y_0$、$x'(t_0) =v_0$和$y'(t_0) = w_0$。
我们可以利用数值方法（如欧拉法、龙格-库塔法等）求解上述一阶微分方程组，从而得到$v(t)$和$w(t)$的数值解。
一旦我们得到了$v(t)$和$w(t)$的数值解，我们可以进行更迭代的计算，从而得到$x(t)$和$y(t)$的数值解。
以上就是利用降阶法求解二阶微分方程组的基本步骤。
下面，我们将通过一个例子来演示具体的计算过程。
考虑方程组：$\begin{cases} x''(t) = -x(t) + x'(t) + \cos(t) \\ y''(t) = -2x(t) + y(t) + \sin(t) \end{cases}$我们希望求解在$t = 0$时，$x(0) = 0$、$y(0) = 1$、$x'(0) =1$和$y'(0) = 0$的初始条件下，方程组的解。
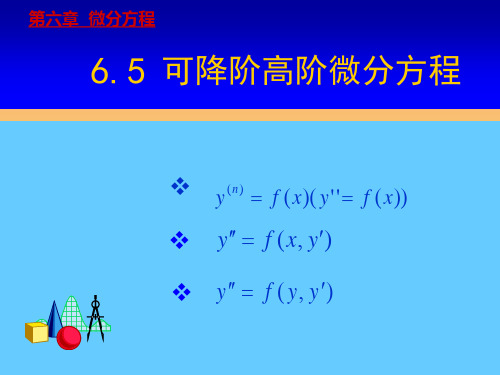
可降阶的二阶微分方程可降阶的二阶微分方程是指在求解过程中可以通过一些变换将其降为一阶微分方程的形式。
这种方程在物理学、工程学等领域中经常出现，因此掌握其求解方法对于理工科学生来说非常重要。
我们来看一个典型的可降阶的二阶微分方程：$$y''+p(x)y'+q(x)y=f(x)$$其中，$p(x)$和$q(x)$是已知函数，$f(x)$是已知的非齐次项函数，$y$是未知函数。
我们可以通过一些变换将其降为一阶微分方程的形式。
我们令$y'=z$，则原方程可以写成：$$z'+p(x)z+q(x)y=f(x)$$接下来，我们再令$u(x)=\int p(x)dx$，则上式可以写成：$$\frac{d}{dx}(e^{u(x)}z)+e^{u(x)}q(x)y=e^{u(x)}f(x)$$这是一个一阶线性微分方程，我们可以通过求解它来得到原方程的解。
具体来说，我们可以先求解其齐次方程：$$\frac{d}{dx}(e^{u(x)}z)+e^{u(x)}q(x)y=0$$这个方程的通解可以表示为：$$z=c_1e^{-u(x)}-\int e^{-u(x)}q(x)ydx$$其中，$c_1$是常数。
接下来，我们可以利用常数变易法来求解非齐次方程的特解。
假设特解为$z=u(x)v(x)$，则代入原方程得到： $$\frac{d}{dx}(e^{u(x)}u'(x)v(x))+e^{u(x)}q(x)y=f(x)$$化简后得到：$$u'(x)e^{u(x)}v(x)=\frac{1}{e^{u(x)}}\int e^{u(x)}f(x)dx$$因此，特解可以表示为：$$z=u(x)v(x)=\int e^{-u(x)}\left(c_2+\int e^{u(x)}f(x)dx\right)dx$$将特解和通解相加，即可得到原方程的通解：$$y=c_1\int e^{-u(x)}dx+\int e^{-u(x)}\left(c_2+\int e^{u(x)}f(x)dx\right)dx$$这就是可降阶的二阶微分方程的求解方法。
