高中数学易错题举例解析(学生版)

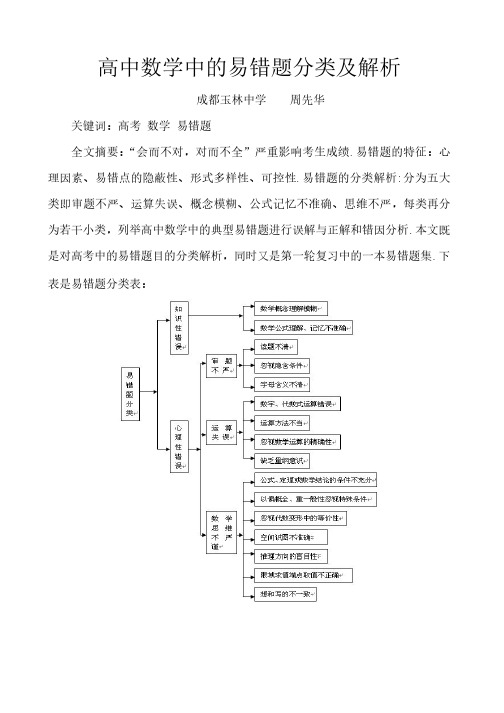
高中数学中的易错题分类及解析高中数学中的易错题分类及解析成都玉林中学成都玉林中学 周先华周先华周先华关键词：高考关键词：高考 数学数学 易错题易错题全文摘要：“会而不对，对而不全”严重影响考生成绩“会而不对，对而不全”严重影响考生成绩..易错题的特征：心理因素、易错点的隐蔽性、形式多样性、可控性理因素、易错点的隐蔽性、形式多样性、可控性..易错题的分类解析易错题的分类解析::分为五大类即审题不严、运算失误、概念模糊、公式记忆不准确、思维不严，每类再分为若干小类，列举高中数学中的典型易错题进行误解与正解和错因分析为若干小类，列举高中数学中的典型易错题进行误解与正解和错因分析..本文既是对高考中的易错题目的分类解析，同时又是第一轮复习中的一本易错题集是对高考中的易错题目的分类解析，同时又是第一轮复习中的一本易错题集..下表是易错题分类表：表是易错题分类表：正 文数学学习的过程，从本质上说是一种认识过程，其间包含了一系列复杂的心理活动数学学习的过程，从本质上说是一种认识过程，其间包含了一系列复杂的心理活动..从数学学习的认知结构上讲，数学学习的过程就是学生头脑里的数学知识按照他自己理解的深度与广度，结合自己的感觉、知觉、记忆、思维与联想，组合成的一个整体结构知觉、记忆、思维与联想，组合成的一个整体结构..所以，数学中有许多题目，求解的思路并不繁杂，但解题时，由于读题不仔细，或者对某些知识点的理解不透彻，或者运算过程中没有注意转化的等价性，或者忽略了对某些特殊情形的讨论……等等原因，都会导致错误的出现.“会而不对，对而不全”，一直以来都是严重影响考生数学成绩的重要因素都是严重影响考生数学成绩的重要因素. .一．易错题的典型特征解题出错是数学答题过程中的正常现象，它既与数学学习环境有关它既与数学学习环境有关,,又与试题的难易程度有关又与试题的难易程度有关..同时也与考生的数学水平、身体与心理状况有关与考生的数学水平、身体与心理状况有关. .1．考生自我心理素质：数学认知结构是数学知识的逻辑结构与学生的心理结构相互作用的产物：数学认知结构是数学知识的逻辑结构与学生的心理结构相互作用的产物..而数学解题是考生主体感受并处理数学信息的创造性的心理过程题是考生主体感受并处理数学信息的创造性的心理过程..部分考生题意尚未明确，加之考试求胜心切，仅凭经验盲目做题，以至于出现主观认识错误或陷入主观思维定势，造成主观盲动性错误和解题思维障碍凭经验盲目做题，以至于出现主观认识错误或陷入主观思维定势，造成主观盲动性错误和解题思维障碍. . 2．易错点的隐蔽性：数学知识的逻辑结构是由数学知识之间的内在的联系联结而成的整体，而其心理结构是指智力因素及其结构，即观察力、记忆力、想象力、注意力和思维力等五个因素组成构是指智力因素及其结构，即观察力、记忆力、想象力、注意力和思维力等五个因素组成..数学解题是考生借助特定“数学语言”进行数学思维的过程，在这个过程中考生的数学知识结构和数学思维习惯起着决定性的作用个体思维的跳跃性是产生思维漏洞的根本原因，这种思维漏洞一旦产生，考生自己是很难发现的，因此易错点的隐蔽性很强现的，因此易错点的隐蔽性很强. .3．易错点形式多样性：根据数学学习的一般过程及数学认知结构的特点，数学易错点一般有知识性错误和心理性错误两种等形式：而知识性错误主要包括数学概念的理解不透彻、数学公式记忆不准确两方面；心理性错误包括审题不严、运算失误、数学思维不严谨等心理性错误包括审题不严、运算失误、数学思维不严谨等. .4．易错题的可控性：学生的认识结构有其个性特点：学生的认识结构有其个性特点..在知识总量大体相当的情况下，有的学生对知识不仅理解深刻，而且组织得很有条理，便于储存与撮；相反，有的学生不仅对知识理解肤浅，而且支离破碎，杂乱无章，这就不利于储存，也不容易提取杂乱无章，这就不利于储存，也不容易提取..在学生形成了一定的数学认知结构后，一旦遇到新的信息，就会利用相应的认知结构对新信息进行处理和加工，随着认识活动的进行，学生的认知结构不断分化和重组，并逐渐变得更加精确和完善，所谓“吃一堑长一智”组，并逐渐变得更加精确和完善，所谓“吃一堑长一智”..只要我们在容易出错的地方提高警戒意识，建立建全解题的“警戒点”立建全解题的“警戒点”,,养成严谨的数学思维好习惯，易错点就会逐渐减少养成严谨的数学思维好习惯，易错点就会逐渐减少. .二、易错题的分类解析1.数学概念的理解不透数学概念所能反映的数学对象的属性，不仅是不分精粗的笼统的属性，它已经是抓住了数学对象的根本的、最重要的本质属性本的、最重要的本质属性..每一个概念都有一定的外延与内涵每一个概念都有一定的外延与内涵..而平时学习中对概念本质的不透彻，对其外延与内涵的掌握不准确，都会在解题中反映出来，导致解题出错延与内涵的掌握不准确，都会在解题中反映出来，导致解题出错. . 例1.若不等式ax 2+x+a +x+a＜＜0的解集为的解集为 Φ，则实数a 的取值范围（的取值范围（ ）） A.a A.a≤≤-21或a ≥21 B.a B.a＜＜21 C.-21≤a ≤21 D.a D.a≥≥21【错解】选A.A.由题意，方程由题意，方程ax 2+x+a=0的根的判别式20140a D <Û-<Û a a≤≤-21或a ≥21，所以选A.【错因分析】对一元二次不等式与二次函数的图象之间的关系还不能掌握，忽视了开口方向对题目的影响忽视了开口方向对题目的影响. .【正确解析】【正确解析】D D .不等式ax 2+x+a +x+a＜＜0的解集为的解集为 Φ，若a=0,a=0,则不等式为则不等式为x<0解集不合已知条件，则a 0¹；要不等式ax 2+x+a +x+a＜＜0的解集为的解集为 Φ，则需二次函数y=ax 2+x+a 的开口向上且与x 轴无交点，所以a>0且20140120a a a ìD £Û-£Û³í>î.例 2. 命题“若△ABC 有一内角为3p，则△ABC 的三内角成等差数列”的逆命题是（的三内角成等差数列”的逆命题是（ ） A ．与原命题真值相异．与原命题真值相异 B ．与原命题的否命题真值相异．与原命题的否命题真值相异 C ．与原命题的逆否命题的真值不同．与原命题的逆否命题的真值不同 D ．与原命题真值相同．与原命题真值相同 【错解】选A.A.因为原命题正确，其逆命题不正确因为原命题正确，其逆命题不正确因为原命题正确，其逆命题不正确. .【错因分析】本题容易出现的错误是对几个概念的理解失误：逆命题——将原命题的题设和结论交换、否命题——将原命题的题设和结论同时否定，逆否命题——将原命题的题设和结论交换后再同时否定，原命题与逆命题、否命题与逆命题是两对互为逆否的命题，互为逆否的命题是等价的题与逆命题、否命题与逆命题是两对互为逆否的命题，互为逆否的命题是等价的..【正确解析】选D.D.显然，原命题正确；其逆命题为：显然，原命题正确；其逆命题为：“若△ABC 的三内角成等差数列，则△ABC 有一内角为3p”.也正确，所以选D. 例3.判断函数f(x)=(x －1)xx-+11的奇偶性为____________________ 【错解】偶函数.f(x)=221(1)(1)(1)(1)(1)111x x x x x x x xx++--==+-=---，所以22()1()1()f x x x f x -=--=-=，所以f （x ）为偶函数. 【错因分析】上述解法有两个错误：【错因分析】上述解法有两个错误：11未考虑函数的定义域；未考虑函数的定义域；2.x-1<02.x-1<02.x-1<0，放入根号内后根号前应添负号，放入根号内后根号前应添负号，放入根号内后根号前应添负号. .【正确解析】非奇非偶函数【正确解析】非奇非偶函数.y=f(x).y=f(x).y=f(x)的定义域为：的定义域为：(1)(1)01011101x x xx x x +-³ì+³ÛÛ-£<í-¹-î，定义域不关于原点对称，所以此函数为非奇非偶函数关于原点对称，所以此函数为非奇非偶函数. .例4.(2011四川四川))1l ，2l ，3l 是空间三条不同的直线，则下列命题正确的是（是空间三条不同的直线，则下列命题正确的是（ ））(A)12l l ^，23l l ^13//l l Þ （B ）12l l ^，3//l l Þ13l l ^ (C)123////l l l Þ 1l ，2l ，3l 共面共面 （D ）1l ，2l ，3l 共点Þ1l ，2l ，3l 共面共面【错解】错解一：选A.A.根据垂直的传递性命题根据垂直的传递性命题A 正确；正确；错解二：选C.C.平行就共面；平行就共面；平行就共面；【错因分析】错解一、二都是因为对空间的线线平行、线线垂直、共面等概念的理解不透彻所致【错因分析】错解一、二都是因为对空间的线线平行、线线垂直、共面等概念的理解不透彻所致. .【正确解答】选B.命题A 中两直线还有异面或者相交的位置关系；命题C 中这三条直线可以是三棱柱的三条棱，因此它们不一定共面；命题D 中的三条线可以构成三个两两相交的平面，所以它们不一定共面. 例5.x=ab 是a 、x 、b 成等比数列的( ) A.充分非必要条件充分非必要条件 B.必要非充分条件必要非充分条件 C.充要条件充要条件 D.既非充分又非必要条件既非充分又非必要条件【错解】【错解】C.C.C.当当.x=ab 时，a 、x 、b 成等比数列成立；当a 、x 、b 成等比数列时，x=ab 成立成立 . 【错因分析】对等比数列的定义理解不透【错因分析】对等比数列的定义理解不透. .【正确解析】选D.D.若若x=a=0x=a=0，，x=ab 成立，但a 、x 、b 不成等比数列，不成等比数列， 所以充分性不成立；反之，若a 、x 、b 成等比数列，则2x ab x ab =Û=±，所以x=ab 不一定成立，必要性不成立所以选D. 例6．(1)(1)把三枚硬币一起掷出，求出现两枚正面向上，一枚反面向上的概率把三枚硬币一起掷出，求出现两枚正面向上，一枚反面向上的概率. (2)(2)某种产品某种产品100件，其中有次品5件，现从中任抽取6件，求恰有一件次品的概率. 分析: （1）【错解】三枚硬币掷出所有可能结果有2×2×2=8种，而出现两正一反是一种结果，故所求概率P=.81【正解】在所有的8种结果中，两正一反并不是一种结果，而是有三种结果：正、正、反，正、反、正，反、正、正，因此所求概率,83=P 上述错解在于对于等可能性事件的概念理解不清，所有8种结果的出现是等可能性的，如果把上述三种结果看作一种结果就不是等可能性事件了，应用求概率的基本公式n mP =自然就是错误的. （2） 【错解】由题意知，这种产品的次品率为5%，且每次抽取相互独立，由独立重复实验概率公式，得：6件产品中恰有1件次品的概率为：23210)10051(1005)1(5166=-=C P . 【正解】在上题的解法中有两个错误：第一，100件产品，件产品，其中有其中有5件次品与次品率为5%是两个不同的概念；第二，该实验不是独立重复实验，从100件产品中任抽6件，可当作抽了6次，每次抽1个，但每次抽到次品还是正品，显然直接影响到下一次抽到次品还是正品，显然直接影响到下一次抽到次品或正品的概率，具体地说，如果第一次抽出的是次品，那么次品就少了一个，第二次再抽到次品的概率就小了…这就是说各次实验之间并非独立的，错用了独立重复实验概率公式，正确解法应为：2430.0610059515==CC C P . 2.公式理解与记忆不准数学公式众多，学生在应用公式解决数学问题时，由于理解不准确（例如公式成立的条件未考虑）或记忆不准确，极易导致运算失误.例如公式2(0,0,a b ab a b +³>>当且仅当a=b 时“=”成立）中极易忽略数a,b 均为正和取等号的条件，还有学生把我们常用的一些公式记成下面的一系列错误公式：x x =2，111>Þ<x x，2)(v vu v u v u¢+¢=¢，y x y x a a a log log )(log ×=+等等. 例7.若1,0,0=+>>y x y x ，则yx41+的最小值为___________. 【错解】 yx41+8)2(14422=+³³y x xy，错解原因是忽略等号成立条件. 【正解】 yx41+=945)(4³++=+++yxx y y y x x y x 例8.8. 函数y=sin 4x+cos 4x －43的相位____________，初相为__________ .周期为周期为_________，单调递增区间为____________. 【错解】y=sin 4x+cos 4x －43=1cos 44x ，所以相位为4x ，初相为0，周期为2p，增区间为…. 【错因分析】应先把函数转化为正弦型函数【错因分析】应先把函数转化为正弦型函数..教材中关于相位、初相……的定义是在正弦型函数的基础上.【正确解析】y=sin 4x+cos 4x －43=11cos 4sin(4)442x x p =+.相位为42x p+，初相为2p ，周期为2p，单调递增区间为21[,]()42k k k Z p p -Î.3.审题不严审题，是解题的第一步，考生在审题过程中可能发生读题不清楚、未发现隐含条件及字母的意义含混审题，是解题的第一步，考生在审题过程中可能发生读题不清楚、未发现隐含条件及字母的意义含混不清等错误不清等错误. . （1）读题不清例9.(2011四川四川))已知()f x 是R 上的奇函数，且当0x >时，1()()12xf x =+，则()f x 的反函数的图像大致是大致是【错解】选B.B.因为因为1()2xy =在0x >内递减，且1()()12x f x =+过点（过点（00，2），所以选B. 【错因分析】考生未看清楚题目是求()f x 的反函数的图像的反函数的图像. .【正确解答】A .根据函数与其反函数的性质，原函数的定义域与值域同其反函数的值域、定义域相同.当10,0()1,122x x y ><<Þ<<，所以选A.或者首先由原函数过点（0，2），则其反函数过点（2，0），排除B 、C ；又根据原函数在0x >时递减，所以选A.例10.编号为1，2，3，4，5的五个人，分别坐在编号为1，2，3，4，5的座位上，则至多有两个号码一致的坐法种数为（致的坐法种数为（ ）A ．120 B.119 C.110 D.109 【错解】“至多有两个号码一致”的对立事件是“三个或四个（即五个）号码一致”， 三个号码一致有3252C A 种，四个号码一致仅一种，所以所求的坐法种数为553322552199A C A --=，无选项.多有一盒次品的概率是 . 多有一盒次品的概率是（2）忽视隐含条件1)))y =1, =1, 求828x=－－ －∞, , ].+ y =1 y 的取值范围是[1, [1, ].（3）字母意义含混不清x y5 4.运算错误（1）数字与代数式运算出错2211k k ++2211k k ++（2）运算方法（如公式、运算程序或运算方向等）选择不当导致运算繁杂或不可能得解而出错OQ OP 为 . 2265,2x x OP OP 的值为的值为 22331()3-36【正确解析】666（3）忽视数学运算的精确性，凭经验猜想得结果而出错 AB （4）计量单位缺乏量纲意识x 53300003-x 300003]x -].31006000),3000053-x ]310030000-x )].3100200003=Þt .时y 最大，此时对甲商品资金投入量为9999999775.29999)200003(300002=-=x 元，对乙商品资金投入量为0.0000000225元.，此时甲商品获得利润60000000.000045元.（不管怎样分配，甲商品都赚了投入资金的1999倍的钞票！）【错解三】设对甲种商品投入金额x 元，则乙种商品投资为30000-x 元，获得利润总额为y 元. 由于利润总额单位为万元，故)300005351(100001x x y -+=，令]3100,0[,300000,300002Î-==-t t x t x 则t t y 500003)30000(5000012+--=].3100,0[],2096000)23[(5000012Î+--=t t （元）元）25.230000,(75.2999723=-=Þ=Þx x t . 【错因分析】量纲不统一，对经验公式x Q x P 53,51==的单位理解不清.从量纲角度看，长度立方为体积、长度平方为面积（正如体积的立方根为长度、面积的算术平方根长度一样），x Q 53=的单位由经验公式给出的前提是变量x 的单位万元确定，因此，的单位万元确定，因此，【正解一】设对甲种商品投入金额x 万元，是乙种商品投资为（3-x ）万元，获得的利润总额为y 万元. 由题意，得]3,0[,35351Î-+=x x x y ,设]3,0[,3,32Î-==-t t x t x 则，则，则t t y 53)3(512+-=].3,0[,2021)23(512Î+--=t t2021,]3,0[23m ax =Î=\y t 时当,即43493=-=x ，494333=-=-x . 因此，为获取最大利润，对甲、乙两种商品的的资金投入应分别为0.75万元和2.25万 元，获得的最大利润为1.05万元. 【正解二】设对甲种商品投入金额x 元，则目标函数应该为元，则目标函数应该为 100003531000051xxy -+×==x x -+300005003500001 令]3100,0[,300000,300002Î-==-t t x t x 则则2021)150(5000015003)30000(50000122+--=+-=t t t y 7500300002=-=Þt x （余与解一同）（余与解一同） 5.数学思维不严谨（1）数学公式或结论的条件不充分例23.已知：已知：a>0 , b>0 , a+b=1,a>0 , b>0 , a+b=1,a>0 , b>0 , a+b=1,求求(a+ 1a )2+(b+ 1b)2的最小值的最小值. .【错解】【错解】 (a+ (a+a 1)2+(b+b 1)2=a 2+b 2+21a +21b +4+4≥≥2ab+ab 2+4+4≥≥4abab 1·+4=8.∴(a+a 1)2+(b+b1)2的最小值是8. 【错因分析】上面的解答中，两次用到了基本不等式a 2+b 2≥2ab 2ab，第一次等号成立的条件是，第一次等号成立的条件是a=b=21,第二次等号成立的条件是ab=ab1，显然，这两个条件是不能同时成立的，显然，这两个条件是不能同时成立的..因此，因此，88不是最小值不是最小值. . 【正确解析】原式【正确解析】原式= a = a 2+b 2+21a +21b +4=( a 2+b 2)+(21a +21b )+4=[(a+b)2－2ab]+[(a 1+b 1)－ab2]+4= (1]+4= (1－－2ab)(1+221b a )+4)+4，由，由ab ab≤≤(2ba +)2=41 得：得：11－2ab 2ab≥≥1－21=21, , 且且221b a ≥1616，，1+221b a ≥1717，∴原式，∴原式≥21×17+4=225 ( (当且仅当当且仅当a=b=21时，等号成立时，等号成立))， ∴(a + a 1)2 + (b + b1)2的最小值是252 .例24.已知两正数x,y x,y 满足满足x+y=1,x+y=1,则则z=11()()x y x y++的最小值为的最小值为 . .【错解一】因为对a>0,a>0,恒有恒有12a a+³,从而z=11()()x y x y++³4,4,所以所以z 的最小值是 4. 【错解二】222222()22x y xy z xy xy xy xy xy +-==+-³22(21)-=-，所以z 的最小值是2(21)-. 【错因分析】解法一中，等号成立的条件是11,11,1x y x y x y xy====+=且即且与相矛盾；解法二中，等号成立的条件是2,2xy xy xy ==即，与104xy <£相矛盾相矛盾.. 【正解】z=11()()x y x y ++=1y x xy xy x y +++=21()222x y xy xy xy xy xy xy+-++=+-，令t=xy, 则210()24x yt xy +<=£=，由2()f t t t =+在10,4æùçúèû上单调递减上单调递减,,故当t=14时 2()f t t t =+有最小值334,所以当12x y ==时z 有最小值334.（2）以偏概全，重视一般性而忽视特殊情况以偏概全是指思考不全面，遗漏特殊情况，致使解答不完全，不能给出问题的全部答案，从而表现出思维的不严密性思维的不严密性. .例25．(1)(1)不等式不等式不等式|x+1|(2x |x+1|(2x |x+1|(2x－－1)1)≥≥0的解集为的解集为____________ ____________ (2)(2)函数函数11xy x+=-的定义域为的定义域为 . . 解析：解析：（1）【错解】1[,)2+¥.因为因为|x+1||x+1|³0恒成立，所以原不等式转化为2x-1³0，所以1[,)2x Î+¥ 【错因分析】忽略了当x=x=－－1时|x+1|=0原不等式也成立，即x=-1为不等式的解为不等式的解. .【正确解析】}1{),21[-È+¥.原不等式等价于原不等式等价于|x+1|=0|x+1|=0或2x-1³0，所以解集为1[,){1}2x Î+¥È-. (2) (2) 【错解】【错解】10(1)(1)011xx x x x+³Þ+-³Þ³-或1x £-.【错因分析】两个错误：一是解分式不等式（方程）时未考虑分母不能为0；二是解二次不等式时没有把二次项系数变为正再考虑两根之外或两根之间，从而导致解集出错二次项系数变为正再考虑两根之外或两根之间，从而导致解集出错. .【正解】(1)(1)0(1)(1)010111011x x x x xx x x x +-³+-£ìì+³ÞÞÞ-£<íí-¹¹-îî例26.过点过点(0,1)(0,1)(0,1)作直线，使它与抛物线作直线，使它与抛物线x y 42=仅有一个公共点，这样的直线有（仅有一个公共点，这样的直线有（ ）A.1条B.2条C. 3条D. 0条【错解】设直线的方程为1+=kx y ，联立îíì+==142kx y xy ，得()x kx 412=+，即：01)42(22=+-+x k x k ，再由Δ＝0,0,得得k=1,k=1,得答案得答案A.【错因分析】本题的解法有两个问题，一是将斜率不存在的情况考虑漏掉了，另外又将斜率k=0的情形丢掉了，故本题应有三解，即直线有三条掉了，故本题应有三解，即直线有三条. .【正确解析】C.C.由上述分析，由上述分析，y 轴本身即为一切线，满足题意；解方程01)42(22=+-+x k x k 时，若k=0k=0，，即直线y=1也与抛物线x y 42=仅有一个公共点，又k=1时也合题意，所以有三条直线合题意，选C. （3）解题时忽视等价性变形导致出错 例27.27. （1）已知f(x) = a x +bx，若,6)2(3,0)1(3££££-f f 求)3(f 的范围的范围. . （2）已知集合}1|||{£-=a x x A ，}0330|{2³---=x xx x B ，且F =B A ，求实数a 的取值范围的取值范围.. 解析：（1）【错解】由条件得ïîïíì£+££+£-622303b a b a ②①由②×由②×22－①－① 156££a ③ ①×①×22－②得－②得 32338-££-b ④ ③+④得 .343)3(310,34333310£££+£f b a 即【错因分析】采用这种解法，忽视了这样一个事实：作为满足条件的函数f(x) f(x) = = a x +bx，其值是同时受b a 和制约的制约的..当a 取最大（小）值时，b 不一定取最大（小）值，因而整个解题思路是错误的不一定取最大（小）值，因而整个解题思路是错误的. .【正确解析】由题意有ïîïíì+=+=22)2()1(b a f b a f , , 解得：解得：解得：)],2()1(2[32)],1()2(2[31f f b f f a -=-=).1(95)2(91633)3(f f ba f -=+=\ 把把)1(f 和)2(f 的范围代入得的范围代入得 .337)3(316££f（2）【错解】由题意，【错解】由题意，A A ：11a x a -££+B ：2300(6)(5)(3)0{|63x x x x x x x x --³Û-+-³Û³-或53}x -££……(后面略后面略)) 【错因分析】求集合B 时，未考虑分式不等式中分母为零这一条件（若B 中不等式为()0f x >或()0f x <形式而不是()0f x ³或()0f x £则不需要考虑此问题）则不需要考虑此问题）. . 【正确解析】由题意，【正确解析】由题意，A=A={|11}x a x a -££+B ：2(6)(5)(3)0300{|6303x x x x x x x x x -+-³ì--³ÛÛ³í-¹-î或53}x -£<由F =B A 则(,6)[4,5)a Î-¥- . 例28.已知数列{}n a 的前n 项和12+=n nS，求.n a【错解】【错解】 .222)12()12(1111----=-=+-+=-=n n n n n n nnS S a【错因分析】【错因分析】 显然，当1=n 时，1231111=¹==-S a ，不满足上述公式，不满足上述公式. .没有注意公式1--=n n n S S a 成立的条件是n 2³.【正确解析】当1=n 时，113a S ==，n 2³时，时，1111(21)(21)222n n n n n n n n a S S ----=-=+-+=-=.所以13(1)2(2)n n n a n -ì=ï=í³ïî.例29.实数a 为何值时，圆012222=-+-+a ax y x 与抛物线x y 212=有两个公共点有两个公共点. . 【错解】【错解】 将圆012222=-+-+a ax y x 与抛物线与抛物线 x y 212=联立，消去y ， 得 ).0(01)212(22³=-+--x a x a x ①①因为有两个公共点，所以方程①有两个相等正根，得ïïîïïíì>->-=D .01021202a a ，， 解之得.817=a 【错因分析】如下图（【错因分析】如下图（11）（2）.显然，当0=a 时，圆与抛物线有两个公共点时，圆与抛物线有两个公共点. .11143q q q qq q 43x y O 图1x y O 图2（4）空间识图不准数学运算能力包括空间想象能力数学运算能力包括空间想象能力数学运算能力包括空间想象能力..空间想象能力是指能根据条件作出正确的图形，根据图形想象出直观形象；能正确地分析出图形中基本元素及其相互关系；能对图形进行分解、组合与变换；会运用图形与图表等手段形象地揭示问题的本质．表等手段形象地揭示问题的本质．对图形的想象主要包括有图想图和无图想图两种，是空间想象能力高层次的标志．而空间识图不准导致的立何几何题目出错情况很多. 例31．直二面角α－l －β的棱l 上有一点A ，在平面α、β内各有一条射线AB ，AC 与l 成450，AB b a ÌÌAC ,，则∠BAC= . 【错解】如右图由最小角定理，12221cos cos cos 2223BAC BAC pq q Ð=×=´=ÞÐ=【错因分析】错解中忽视了AC 的另一位置OD OD，此时，此时23BAD p Ð=.【正确解析】3p或23p .如下图.当6CAF pÐ=时，由最小角定理，12221cos cos cos 2223BAC BAC p q q Ð=×=´=ÞÐ=；当AC 在另一边DA 位置时，23BAC pÐ=.（5）推理方向的盲目性根据题的已知条件及所求的特征，有时直接从已知出发，运用公式、定理等得结论，这是综合法；有时需要从结论出发，分析它的必要条件，直到得到一个明显成立的命题，时需要从结论出发，分析它的必要条件，直到得到一个明显成立的命题，这是分析法这是分析法.这是两种不同的推理方向，如果解题时失主理方向不正确，可能导致解题思路受阻或出错. 例32.32. 设f f ( ( ( x x x ) ) ) = = = x x 3－21x 2－2x ＋5，当]2,1[-Îx 时，f f ( ( ( x x x ) ) ) < < < m m 恒成立，则实数m 的取值范围为 . 【错解】m>72.令2'()320f x x x =-->，得f(x)的增区间为2(,),(1),(1,,)3-¥-+¥，f(-1)=112（区间左端点），7(1)2f =(极小值点)，所以]2,1[-Îx 时min 7()2f x =所以m>72.【错因分析】推理方向的不正确，f ( x ) < m 恒成立应理解为max ()m f x >而不是min ()m f x >. 【正确解析】m>7.由题意，f f ( ( ( x x x ) ) ) < < < m m 恒成立即max ()m f x >.令2'()320f x x x =-->，得f(x)的增区间为2(,),(1),(1,,)3-¥-+¥，且f(2)=7，2()73f -<，结合f(x)的草图知，max()7f x =，所以m>7.（6）限域求值端点取值不正确例33.若31<<-x ,则_____________;__________112ÎÎ-x x()])的取值范围是的取值范围是 . .1,3,sin,sin 426636232£Þ£Þ£+£==)36p +£.【错因分析】当2663£+£时，根据正弦函数的图象，)6+[,1]23[,]222,42663p p p p p £Þ£Þ£+£)6p+1[,1]2n (6+（7）说一套做一套，粗枝大叶，心里想的和手上写的不一致tan tan 1=-+=BA 4=. 。

高中高考数学易错易混易忘题分类汇总及解析高考数学易错易混易忘题分类汇总及解析“会而不对，对而不全”一直以来成为制约学生数学成绩提高的重要因素，如何解决这个问题对决定学生的高考成败起着至关重要的作用。

本文结合学生在考试中常见的29个易错、易混、易忘典型题目，这些问题也是高考中的热点和重点，做到力避偏、怪、难，进行精彩剖析并配以近几年的高考试题作为相应练习，一方面让你明确这样的问题在高考中确实存在，另一方面通过作针对性练习帮你识破命题者精心设计的陷阱，以助你在高考中乘风破浪，实现自已的理想报负。

【易错点1】忽视空集是任何非空集合的子集导致思维不全面。

例1、设a??x|x2?8x?15?0?，b??x|ax?1?0?，b若ab?，谋实数a共同组成的子集的子集存有多少个？【易错点分析】此题由条件ab?b易知b?a，由于空集就是任何非空集合的子集，但在解题中极容易忽略这种b?b知b特殊情况而造成求解满足条件的a值产生漏解现象。

解析：子集a化简得a??3,5?，由a?a故（ⅰ）当b??时，即为方程ax?1?0难解，此时a=0符合已知条件（ⅱ）当b??时，即方程ax?1?0的解为3或5，代入得a?11或。

综上满足条件的a组成的集合为35?11?3?0,,?，故其子集共有2?8个。

?35?【知识点归类点拔】（1）在应用条件a∪b＝ｂ?a∩b＝ａ?ａ集φ的情况优先进行讨论．（2）在答疑子集问题时，必须特别注意子集的性质“确定性、无序性、互异性”特别就是互异性对子集元素的管制。

有时须要展开检验解的结果就是满足用户子集中元素的这个性质，此外，解题过程中要特别注意子集语言（数学语言）和自然语言之间的转变例如：ｂ时，要树立起分类讨论的数学思想，将集合ａ是空ax,y?|x2?y2?4?，bx,y?|?x?3y?4?22?r2?，其中r?0,若ab??谋r的值域范围。

将集合所表达的数学语言向自然语言进行转化就是：集合a表示以原点为圆心以2的半径的圆，集合b表示以（3，4）为圆心，以r为半径的圆，当两圆无公共点即两圆相离或内含时，求半径r的取值范围。

高中数学必修二第七章复数重点易错题单选题1、设a∈R，若复数(1+i)(a+i)在复平面内对应的点位于实轴上，则a=（）A．0B．−1C．1D．√2答案：B分析：利用复数乘法化简复数，根据其对应点在实轴上有a+1=0，即可得答案. ∵复数(1+i)(a+i)=(a−1)+(a+1)i在复平面内对应的点位于实轴上，∴a+1=0，即a=−1．故选：B2、z=(2+i)2−4在复平面内对应的点位于（）A．第一象限B．第二象限C．第三象限D．第四象限答案：B分析：将复数化为标准形式再根据复数的几何意义即可确定.z=(2+i)2−4=−1+4i，则z在复平面内对应的点位于第二象限，故选：B.3、已知复数z满足1−zz=1−i，则z=（）A．−25+15i B．−25−15i C．25+15i D．25−15i答案：D分析：由已知条件求出复数z，利用共轭复数的定义可得出结果.因为1−zz =1−i，所以，z=12−i=2+i(2−i)(2+i)=25+15i，因此，z=25−15i.故选：D.4、在复平面内，复数z=5i3−4i（i为虚数单位），则z对应的点的坐标为（）A．(3,4)B．(−4,3)C．(45,−35)D．(−45,−35)分析：根据复数运算法则进行运算后，再由复数的几何意义得解.因为z=5i3−4i =5i(3+4i)(3−4i)(3+4i)=3i−45=−45+35i，所以z=−45−35i，所以复数z所对应的点的坐标为(−45,−35).故选:D.5、复数2i1−i（i是虚数单位）的虚部是（）A．1B．−i C．2D．−2i答案：A分析：利用复数的除法法则及复数的概念即可求解.由题意可知，2i1−i =2i×(1+i)(1−i)(1+i)=−2+2i2=−1+i，所以复数2i1−i的虚部为1.故选：A.6、设i是虚数单位，则复数z=2i(−2+3i)对应的点在复平面内位于（）A．第一象限B．第二象限C．第三象限D．第四象限答案：C分析：利用复数的乘法法则化简复数z，由此可得出结论.∵z=2i(−2+3i)=−6−4i，因此，复数z在复平面内的点位于第三象限.故选：C.7、已知a∈R，(1+ai)i=3+i，(i为虚数单位)，则a=（）A．−1B．1C．−3D．3答案：C分析：首先计算左侧的结果，然后结合复数相等的充分必要条件即可求得实数a的值. (1+ai)i=i+ai2=i−a=−a+i=3+i，利用复数相等的充分必要条件可得：−a=3,∴a=−3.8、已知i为虚数单位，则1+3i1−2i=（）. A．−2−3i B．−1−iC．−1+i D．3+2i答案：C分析：利用复数的除法化简可得结果.1+3i 1−2i =(1+3i)⋅(1+2i)(1−2i)⋅(1+2i)=−5+5i5=−1+i，故选：C.多选题9、已知复数z=1+i1−i，以下结论正确的是（）A．z2021是纯虚数B．|z+i|=2C．z⋅z̅=−1D．在复平面内，复数z̅+z⋅i对应的点位于第三象限答案：ABD分析：利用复数除法运算法则化简可得z=i，根据i的幂运算的周期性、模长的定义、共轭复数定义和复数的乘法运算、复数对应的点坐标来依次判断各个选项即可.z=1+i1−i=(1+i)(1+i)(1−i)(1+i)=2i2=i对于A，∵z2021=i2021=i4×505+1=i，∴z2021为纯虚数，A正确；对于B，|z+i|=|2i|=2，B正确；对于C，z⋅z̅=i⋅(−i)=−i2=1，C错误；对于D，∵z̅+z⋅i=−i+i2=−1−i，∴z̅+z⋅i对应的点为(−1,−1)，位于第三象限，D正确. 故选：ABD.10、若复数z在复平面对应的点为Z，则下来说法正确的有（）A．若|z|=3，则Z在复平面内的轨迹为圆B．若|z+4|+|z−4|=8，则Z在复平面内的轨迹为椭圆C．不可能存在复数z同时满足|z|=3和|z+4|+|z−4|=10D．若|z|=3，则|z+4|+|z−4|的取值范围为[8，10]答案：AD分析：设z=x+y i，x，y∈R，根据题中的条件得到相应的轨迹，再分析、判断、计算可求解.对于A，设z=x+y i,x，y∈R，则有|z|=√x2+y2=3⇒x2+y2=9，可知Z在复平面内的轨迹为圆，故A 正确；对于B，设z=x+yi,x，y∈R且|z+4|+|z−4|=8，所以√(x+4)2+y2+√(x−4)2+y2=8=8，所以z在复平面内的轨迹是以(−4,0)和(4,0)为端点的线段，故B不正确；对于C，设z=x+yi,x，y∈R且|z+4|+|z−4|=8，所以√(x+4)2+y2+√(x−4)2+y2=10>8，所以z在复平面内的轨迹是以(−4,0)和(4,0)为焦点，长轴为10的椭圆，其方程为x225+y29=1，若|z|=3，则有x2+y2=9，两者联立{x225+y29=1x2+y2=9，有解x=0，y=±3，所以存在复数z同时满足|z|=3和|z+4|+|z−4|=10，故C不正确；对于D，设z=x+y i,x，y∈R，若|z|=3，则有x2+y2=9，令t=|z+4|+|z−4|=√(x+4)2+y2+√(x−4)2+y2=√x2+y2+16+8x+√x2+y2+16−8x=√25+8x+√25−8x则t2=50+2√252−64x2，（−3≤x≤3）令y=252−64x2，可得72≤y≤252，所以64≤t2≤100，于是得8≤t≤10，故D正确.故选：AD11、设Z1，Z2，Z3为复数，下列命题中错误的是（）A．|Z1|2=Z12B．|Z1⋅Z2|=|Z1|⋅|Z2|C．若Z1+Z2∈R，则Z1−Z2为纯虚数D．若Z2=Z3，且Z1≠0，则|Z2Z1|=|Z3Z1|答案：AC分析：根据举例说明即可判断A、C；根据复数的乘法运算和几何意义即可判断B；根据共轭复数的概念和除法运算即可判断D.A：取Z1=i，则|Z1|2=1，Z12=i2=−1，故A错误；B：设Z1=a+b i，Z2=c+d i(a、b、c、d∈R)，则Z1⋅Z2=(a+b i)(c+d i)=(ac−bd)+(ad+bc)i，|Z1⋅Z2|=√(ac−bd)2+(ad+bc)2=a2c2+a2d2+b2c2+b2d2，又|Z1|⋅|Z2|=√(a2+b2)(c2+d2)=a2c2+a2d2+b2c2+b2d2，所以|Z1⋅Z2|=|Z1|⋅|Z2|，故B正确；C：取Z1=Z2=0，则Z1−Z2=0为实数，故C错误；D：由Z2=Z3，得Z2=Z3，则|Z1Z2|2−|Z1Z3|2=(Z1Z2)(Z1Z2)−(Z1Z3)(Z1Z3)=0，所以|Z1Z2|=|Z1Z3|，又Z1≠0，所以|Z2||Z1|=|Z3||Z1|，故D正确.故选：AC.填空题12、已知复数z1＝3－bi，z2＝1－2i，若z1z2是实数，则实数b＝________. 答案：6分析：化简z1z2，利用虚部为零，计算出b即可.z1 z2＝3−bi1−2i＝(3−bi)(1+2i)(1−2i)(1+2i)＝3+2b+(6−b)i5，∵z1z2是实数，∴6－b＝0，即b＝6.所以答案是：613、已知a为实数，若复数z=(a2−3a−4)+(a−4)i为纯虚数，则a=________．答案：−1分析：根据纯虚数的定义列出方程，解得，即可得出答案.解：若复数z=(a2−3a−4)+(a−4)i是纯虚数，则{a 2−3a −4=0a −4≠0，解得a =−1. 所以答案是：−1.14、实部为5，模与复数4−3i 的模相等的复数的个数为______.答案：1解析：设z =5+bi(b ∈R)，根据模长关系建立等式求解即可.依题意设z =5+bi(b ∈R)，则|z|=√25+b 2，而|4−3i|=√42+(−3)2=5，所以√25+b 2=5，即b =0.所以z =5.故满足题意的复数只有一个.所以答案是：1小提示：此题考查复数概念的辨析和模长的计算，关键在于熟练掌握复数相关概念准确辨析求解. 解答题15、已知z 为复数，z +2i 和z 2−i 均为实数，其中i 是虚数单位． (1)求复数|z | ；(2)若复数z 1=z̅+1m−1−7m+2i 对应的点在第四象限，求m 的取值范围．答案：(1)|z | =2√5；(2)−2<m <34或1<m <32分析：（1）设z =a +b i ，得出z +2i 和z2−i ，根据题意即可求出；（2）表示出z 1，根据z 1对应的点在第四象限可得不等关系求解.(1)设z =a +b i ，则z +2i =a +(b +2)i ，z2−i =a+b i2−i =(a+b i )(2+i )(2−i )(2+i )=a−b 5+a+2b 5i ， 因为z +2i 和z 2−i 均为实数，所以{b +2=0a+2b 5=0 ，解得{a =4b =−2 ， 所以z =4−2i ，则|z | =√42+(−2)2=2√5；(2)z 1=4+2i +1m−1−7m+2i =4m−3m−1+2m−3m+2i ，因为z 1对应的点在第四象限，所以{4m−3m−1>02m−3m+2<0 ，解得−2<m <34或1<m <32.。

高一上学期易错陷阱总结1、 对数型函数中，（易忽略真数位置大于0）5．已知y ＝log a (2－ax )在[0,1]上为减函数，则a 的取值范围为( ) A ．(0,1) B ．(1,2) C ．(0,2) D ．[2，＋∞) 2、 集合中，空集的特殊性（易忘记讨论空集）13．已知集合A ＝{x |2a ＋1≤x ≤3a －5}，B ＝{x |x ＜－1，或x ＞16}，分别根据下列条件求实数a 的取值范围． (1)A ∩B ＝∅； (2)A ⊆(A ∩B )． 3、集合中，元素的互异性（易忽略导致取值错误）[例2] 已知集合⎩⎨⎧⎭⎬⎫1，a ，b a ＝{0，a 2，a ＋b }，求a 2 019＋b 2 020的值．跟踪探究 2.已知集合A ＝{2，x ，y }，B ＝{2x,2，y 2}且A ＝B ，求x ，y 的值．4、集合中，元素的特殊要求（比如：易忽略x等条件）跟踪探究 1.若集合A ＝{x |1≤x ≤3，x ∈N }，B ＝{x |x ≤2，x ∈N }，则A ∩B ＝( )A.{x |1≤x ≤2} B ．{x |x ≥1} C ．{2,3}D ．{1,2}5、抽象函数的定义域问题（定义域仅代表x ，括号内取值范围一致）14、函数的定义域为,则的定义域是___;函数的定义域为___.6、 区间中默认a<b14.已知函数f （x ）=, x是偶函数，则a+b=7、 换元法求值域类问题（易忽略换元后，t 的取值范围）(1)f (x ＋1)＝x ＋2x ，求f (x )的值域；8、动轴定区间类问题（分类讨论不重不漏）典型案例：求函数y ＝x 2－2ax －1在[0,2]上的最值．9同增异减求单调区间问题（对数型时不能忽略真数位置大于0）（多个区间，隔开）跟踪探究 2.求函数y ＝log 2(x 2－5x ＋6)的单调区间．10、分段函数单调性问题。

（易忽略结点处）13．已知函数f (x )＝⎩⎪⎨⎪⎧x 2－ax ＋4，(x ≤1)，－ax ＋3a －4，(x ＞1)且f (x )在R 上递减，则实数a 的取值范围________．11.解分式不等式。

高中数学易错题举例解析高中数学中有许多题目，求解的思路不难，但解题时，对某些特殊情形的讨论，却很容易被忽略。

也就是在转化过程中，没有注意转化的等价性，会经常出现错误。

下面通过几个例子，剖析致错原因，希望能对同学们的学习有所帮助。

加强思维的严密性训练。

● 忽视等价性变形，导致错误。

⎩⎨⎧ x >0 y >0 ⇔ ⎩⎨⎧ x + y >0 xy >0 ，但 ⎩⎨⎧ x >1 y >2 与 ⎩⎨⎧ x + y >3 xy >2不等价。

【例1】已知f(x) = a x + x b，若,6)2(3,0)1(3≤≤≤≤-f f 求)3(f 的范围。

●忽视隐含条件，导致结果错误。

【例2】(1) 设βα、是方程0622=++-k kx x 的两个实根，则22)1()1(-+-βα的最小值是不存在)D (18)C (8)B (449)A (-(2) 已知(x+2)2+ y 24 =1, 求x 2+y 2的取值范围。

●忽视不等式中等号成立的条件，导致结果错误。

【例3】已知：a>0 , b>0 , a+b=1,求(a+ 1a )2+(b+ 1b)2的最小值。

●不进行分类讨论，导致错误【例4】(1)已知数列{}n a 的前n 项和12+=nn S ，求.n a(2)实数a 为何值时，圆012222=-+-+a ax y x 与抛物线x y 212=有两个公共点。

●以偏概全，导致错误以偏概全是指思考不全面，遗漏特殊情况，致使解答不完全，不能给出问题的全部答案，从而表现出思维的不严密性。

【例5】(1)设等比数列{}n a 的前n 项和为n S .若9632S S S =+，求数列的公比q . (2)求过点)1,0(的直线，使它与抛物线x y 22=仅有一个交点。

《章节易错训练题》1、已知集合M = {直线} ，N = {圆} ，则M ∩N 中元素个数是 (A) 0 (B) 0或1 (C) 0或2 (D) 0或1或22、已知A = {}x | x 2+ tx + 1 = 0 ，若A ∩R *= Φ ，则实数t 集合T = ___。

高中数学各章节关注点1.4 否定形式命题可考虑用逆否命题来研究．例1.4 已知R b a ∈,，则条件＂21≠≠b a 或＂是＂2≠ab ＂的 条件．1.5 “且”与“或”的区分．例1.5.1 判断真假：(1) 10232≠⇔≠+-x x x 或2≠x ；(2)33≥．例1.5.2 已知 013:1=+-y ax l ，01)21(:2=---ay x a l ，根据下列条件分别求a 的取值范围．(1) 21l l 与相交；(2) 21l l ⊥．2、函数2.1求函数关系式时必须包含定义域；对数问题也应注意定义域．例2.1 (1)在ABC ∆中，BC AC BC x AB ,3,4,===边上的中线长y AM =，求y 关于x 的函数关系式；(2)函数x x y ln 22-=的单调递增区间是 ．2.2 函数的零点问题通常利用函数图像．例2.2 (1)若函数m x x x y -+-=4423在区间），（251-有且只有一个零点，则实数m 的取值范围是 ；(2) 若函数m x x x y -+-=4423在区间），（251-至少有一个零点，则实数m 的取值范围是 ．例2.5.2 已知函数)(x f 是周期为2的周期函数，当20≤<x 时，13)(2+-=x x x f ，求当75<<x 时，函数)(x f 的表达式．2.6 关注二次函数二次项系数是否为零，注意∆、开口、对称轴与特殊值四要素．例2.6 (1)已知方程0)3(42=++-a x ax 有两个大于１的不等实根，求实数a 的取值范围； (2) 已知方程0)3(42=++-a x ax 至少有一个大于１的实根，求实数a 的取值范围．2.7 指对数的运算法则．例2.7 （1）已知02ln =+x ，求x ；（2）已知)00(02≠>=-a a a x且，求x ； （3）解不等式)10(2log <<->a x a ；（4）已知()1,12log 2log >>>b a b a ，求b a , 的大小关系．3、数列3.1 注意题中n 取值，如：⎩⎨⎧≥-==-2n ,S S 1,n ,S a 1n n1n 的公式应用．例3.1 (1)已知数列{}n a 的前n 项的和为）（+∈+-=N n n n S n 1322，求数列{}n a 的通项公式；(2) 已知数列{}n a 的前n 项的和为n S ，若),2(0321+-∈≥=+N n n a S S n n n ，又31=a ，求n a ；(3) 已知数列{}n a 的前n 项的和为n S ，若,)(31++∈=N n a S n n 又31=a ，求n a ．3.2 等比数列求和注意对q=1与q ≠1的分类；等比数列证明注意首项0a 1≠的说明．例3.2 (1) 若等比数列{}n a 的前n 项和为n S ，公比1-≠q ．求证：n n n n n S S S S S 232,,--也成等比；(2) 若数列{}n a 中,)(23,411++∈-==N n a a a n n ．求证数列{}1-n a 是等比数列．3.3 求和：观察通项、 注意首项、 点清项数，并注意结果的验证．例3.3 求和nn S )2(8421-++-+-= ．3.4 应用性问题：逐步列式，保留原始数据，便于观察规律．例3.4 小王2012年5月向银行借款100万元用于购房，年利率7.8%，2013年5月开始偿还，每年还a 万元，2032年5月全部还清，求每年还款额a （其中2078.110≈）．3.5 等差数列、等比数列常用定义、公式或性质解决．例3.5.1 已知数列{}n a 的前n 项的和为n S ，42,293==S S ．(1)若数列{}n a 成等差，求12S ； (2) 若数列{}n a 成等比，求12S ．例3.5.2 已知等差数列{}n a 与{}n b 的前n 项的和分别为n n T S , , 若1423--=n n T S n n , 求2020b a ．3.6 数列与函数的单调性、最值研究的方法“区别”．例3.6 (1) 已知数列{}n a 的通项公式是nnn C a )31(2012⋅=，求数列{}n a 的最大项；(2)已知函数xex x f 2012)(-=，求函数)(x f 在区间),0(∞+上的最大值．3.7 熟练掌握利用错位相减法或裂项法进行数列求和． 例3.7 (1) 求和：n n n S )21)(12()21(7)21(5)21(321432--++-+-+-+-= ；(2) 求和：)12(753197531753153131++++++++++++++++=n S n ．(3) 求数列⎭⎬⎫⎩⎨⎧+++)23(3522n n n n 的前n 项的和n T ．3.8 通常递推关系转化为“新数列”的思想运用． 例3.8 已知数列{}n a 中，311=a ,根据下列各递推公式，求数列的通项公式： （1） 131-=+n n a a ；（2）131+=+n nn a a a ；（3）()112++-=n n n n a a a a ；（4）nn n a a 331=+－．5.4 三角形问题应注意内角的判断一个或两个解．例5.4 (1) 在ABC ∆中，若32cos ,36sin ==B A , 求C sin ；(2) 在ABC ∆中，若3,31cos ,33sin ===a B A , 求边c 的长．5.5 熟练掌握正弦、余弦定理，面积公式．例5.5.1 在ABC ∆中， 面积32=S ，,6,600=+=c b A （1）求边a 的长； (2)求)(sin C B -．例5.5.2 在ABC ∆中, 三内角C B A ,,成等差数列 , 角C B A ,,所对应的边分别为c b a ,,, 外接圆半径为2 , 求22c a +的取值范围．6.5 熟练掌握不等式应用的两种题型.例6.5 (1) 已知+∈R y x ,，212=+yx ，求y x +的最小值；（2）已知c ax x f +=2)(，1)1(2≤≤-f ，4)2(0≤≤f ，求)3(f 的取值范围．7、直线和圆7.1 求直线问题注意斜率存在与不存在，掌握斜率变化与倾斜角变化的规律．例7.1 (1) 已知过点（０，１）的直线l 与圆)0()1(222>=++R R y x 交于B A ,两点，O 为坐标原点，若52<⋅<-OB OA ，求半径R 的取值范围；(2) 已知过点（－２，０）的直线l 与圆16)1(22=++y x 交于B A ,两点，O 为坐标原点，若1213-<⋅<-OB OA ，求直线l 的倾斜角取值范围．高中数学各章节关注点答案3.1解：(1) ⎩⎨⎧≥== 2.n ,5-4n ,1n ,0a n (2) ,0)(3211=-+--n n n n S S S S 32111=--n n S S ， 数列⎭⎬⎫⎩⎨⎧n S 1是首项为31，公差为32的等差数列，所以3121-=n S n ，即123-=n S n ，从而得⎪⎩⎪⎨⎧≥---==.2,)32)(12(61,3n n n n a n ， (3) ,43111n n n n n n S S S S a S =⇒-==+++数列{}n S 是公比为4 , 首相为3的等比数列 ,所以143-⋅=n n S , 从而⎩⎨⎧≥⋅==-.2,49,1,32n n a n n 3.2解：(1)当公比1=q 时，,,,0123121na S S na S S na S n n n n n =-=-≠=结论成立；当公比1≠q 时，222212131123)1()1()1)1(1)1((1)1()(q q q a q q a q q a q q a S S S nn n n n n n n --=-----⋅--=-， 22221212122)1()1(1)1(1)1()(q q q a q q a q q a S S n n n n n n--=⎥⎦⎤⎢⎣⎡-----=-， 1,0,01±≠≠≠q q a ，0)()(2322≠-=-∴n n n n n S S S S S ，结论成立．(2),)1(311-=-+n n a a 又0311≠=-a ，所以数列{}1-n a 是以3为首项,以3为公比的等比数列．3.3解： []11)2(131)2(1)2(1++--=----=n n n S ． 3.4解：201819%)8.71(100%)8.71(%)8.71(%)8.71(+=+++++++a a a a ，2020%)8.71(100%)8.71(1%)8.71(1+=+-+-⋅a ， 4.103078.0400=⨯≈a （万元）．3.5.1解：(1)由91269363,,,S S S S S S S ---成等差，得,)42(2)2(266S S -+=-166=S ，所以38912=-S S ，8012=∴S ．(2) 由91269363,,,S S S S S S S ---成等比，得,)42(2)2(626S S -=-86-=S 或106=S ，从而128912=-S S 或250912-=-S S ，所以17012=S 或20812-=S ．3.5.2解：利用等差数列求和公式n n a n S )12(12-=-得312315511539392020===T S b a ． 3.6解：(1)1)1(3201231!)2011(!)1(!2012!)2012(!!2012312012120121≥+-=⋅-+-=⋅=++n nn n n n C C a a n n n n ，得25.502≤n ，即12502503a a a a >>>> ， >>>505504503a a a ，所以数列{}n a 的最大项为5035032012503)31(C a =．(2)2013,02013)('==-=x exx f x得，函数↑∞+↑），（，），）在（（201320130x f ． 所以函数)(x f 在区间),0(∞+上的最大值是2013)2013-=ef （．3.7解：(1) 运用错位相减法，15432)21)(12()21)(32()21(7)21(5)21(3)21(21+--+--++-+-+-+-=-n n n n n S15432)21)(12(])21()21()21()21()21[(22123+----++-+-+-+-+-=n n n n S 1111)(12()21(13121)21)(12()21(1)21(141221+-+---⎥⎦⎤⎢⎣⎡--+-=---⎥⎦⎤⎢⎣⎡----⋅+-=n n n n n n n n )21(61661-++-=， nn n S )21(91691-++-=∴．(2) )211(21)2(1)12(7531+-=+=+++++n n n n n，⎥⎦⎤⎢⎣⎡+-++--++-+-+-+-=∴)211()1111()6141()5131()4121()311(21n n n n S n )2)(1(23243211121121+++-=⎥⎦⎤⎢⎣⎡+-+-+=n n n n n ． (3) )2(31)1(31)23(35212+-+=+++-n n n n n n n n,))2(31)1(31()531431()431331()33121(1322+-+++⨯-⨯+⨯-⨯+⨯-=∴-n n T n n n)2(3121+-=n n ．4.9解：y x y x 32cos 2sin -=+,22)32()2(1y y -≥+,031252≤+-y y ,52165216+≤≤-y , ∴值域为⎥⎦⎤⎢⎣⎡+-5216,5216． 4.10解：321sin 121,21sin 23,1sin 21,326<+≤≤+<≤<∴≤<x x x x ππ， 所以1sin 43+-=x y 的值域为⎥⎦⎤ ⎝⎛1,31．4.11解: 2tan 11tan )4tan(=-+=+x x x π, 得31tan =x ． (1)原式671tan 32tan =++=x x ．(2)原式7201tan tan )1(tan 2)cos (sin cos sin )cos (sin 2222222-=--+=+-+=x x x x x x x x x ． 5.1 (1)51- 解析：CB AB AC AB CB BC AB CB AM ⋅-+=⋅+=⋅)](32[)32( 51)2716236(31231)()2(3122-=--=⎥⎦⎤⎢⎣⎡⋅+-=-⋅+=AC AB AC AB AC AB AC AB ．(2)42- 解析：以A 为原点，分别以AB ，AC 所在直线为x ，y 轴，建立直角坐标系，A （0，0），B （6，0），C （0，9），M （2，6），425412),9,6(,)6,2(-=-=⋅-==CB AM CB AM ．5.2解：(1)213,0372)2(1)1)(23(2-=-==++⇒-⋅=++x x x x x x x 或得． (2) 26,03201)23()1)(2(2±==-⇒=⋅+++-x x x x x 得． 5.3解：(1)错 解析：0应该为0．(2)错 解析：c b a )(⋅与向量c 共线 , )(c b a ⋅与向量a 共线． (3)错 解析：正确形式为AC BC AB =+；(4) 错 解析：正确形式为CB AC AB =-．5.4解：(1),,sin 35sin A B A B <∴<=33cos ±=∴A , B A B A B A C sin cos cos sin )(sin sin +=+= 9156235)33(3236±=±+⋅=． (2) 36cos ,,sin 322sin =∴>∴>=A A AB A B ，必为锐角角 ,935322363133sin cos cos sin )(sin sin =+⋅=+=+=B A B A B A C ； 由正弦定理得539353sin sin =⋅⋅==A C a c ．5.5.1解：(1) 83260sin 210=⇒==bc bc S ， 又，或22,4,6===∴=+b c b c b 4=c ，32,12cos 2222==-+=a A bc c b a ． (2) 当4,2==c b 时，由正弦定理，C B sin 4sin 260sin 320==，得1sin ,21sin ==C B ，23)sin(,90,3000-=-==C B C B ，同理当2,4==c b 时，23)sin(=-C B ． 5.5.2解：三角C B A ,,成等差060=⇔B , 由正弦定理42sin sin ===R CcA a , 所以[][])2240cos(2cos 28)120(sin sin 1602222A A A A c a ---=-+=+)602cos(8160+-=A , 由于001200<<A , 00030060260<+<A ,所以21)602cos(10<+≤-A , 从而241222≤+<c a ． 5.6.1 解: (1)真． (2)假．(3)假. 解析：正确的应是等腰三角形或直角三角形． 例5.6.2 (1) 若角A 为锐角, 则A A cos sin +的取值范围是 ； (2)若角A 为钝角, 则A A cos sin +的取值范围是 ．5.6.2 （1）(]2,1 解析：)45sin(2cos sin +=+A A A ，A 为锐角，900<<∴A ， 1354545<+<∴A ，1)45sin(22≤+<∴A ，即有2cos sin 1≤+<A A .． (2)()1,1- 解析: A 为钝角，即18090<<A ，22545135<+<∴A ，22)45sin(22<+<-∴ A ，即有1cos sin 1<+<-A A ． 6.1解：(1)027322132≥--=---x x x x x , 由此得解集[)⎪⎭⎫⎢⎣⎡∞+,372,0 ．6.4 1024或 解析：)52()(1+=-⋅x x x ，得0=x 或3-=x ，44224)42(222++=++=-x x x x ，40=-=x ；1023=--=x ．6.5 解:(1))223(21)2(321)12)((21+≥⎥⎦⎤⎢⎣⎡++=++=+y x x y y x y x y x ， 即y x +的最小值为)223(21+． (2))1(35)2(389)3(,4)2(,)1(f f c a f c a f c a f -=+=+=+=；332)2(380≤≤f ，310)1(3535≤-≤-f ，14)3(35≤≤-∴f ．则当1=t 时，1=k ，当1≠t 时，0)3)(1(44,0)3(2)1(2≥---=∆=-+--t t t k k t ，得；2222+≤≤-t ，所以24322-<<-R ．综上所述，半径R 的取值范围是⎪⎭⎫ ⎝⎛-24,0．(2) 当x l ⊥轴时，)15,2(-A ，)15,2(--B ，11-=⋅OB OA ，不合, 当l 与x 轴不垂直时，设直线)2(:+=x k y l 代入圆方程，得0154)12(2)1(2222=-++++k x k x k ,由韦达定理，222122211154,1)12(2kk x x k k x x +-=++-=+， 2212212212214)(2)1()2)(2(k x x k x x k x x k x x OB OA ++++=+++=⋅)12,13(1151141)12(41542222222--∈++-=+++--=kk k k k k k ，得312<<k , 13-<<-k 或31<<k ，所以直线l 倾斜角的范围是⎪⎭⎫⎝⎛⎪⎭⎫ ⎝⎛43,323,4ππππ ．7.2解：圆心（－１，０）到直线的距离53=d ，所以5109235322=⎪⎭⎫ ⎝⎛+⎪⎪⎭⎫ ⎝⎛=R ． 8.1.1解：(1)513解析：因为02=+FQ PF ,所以点Q 为线段PF 的中点, O 为原点，椭圆另一焦点为'F ,则OQ PF //', 4'=PF , 由椭圆定义：42-=a PF ,'PF PF PF OQ ⊥⇒⊥,由勾股定理；52)42(162=-+a , 得5=a , 所以椭圆的离心率513=e ． (2) 228- 解析：如图，椭圆左焦点)0,2(-F ， 右焦点即为B ，如图，由椭圆的定义得2288)(8-=-≥--=+AF PA PF PB PA ．8.1.2解： (1) 1622=+y x 解析：不妨设点P 在双曲线的右支上，设直线1与2PF 交于点Q ，O 为坐标原点，4221)(21)(21212122==⋅=-=-==a a PF PF PF PQ Q F OM ， 所以点M 的轨迹方程是1622=+y x ．(2) ２ 解析：抛物线的焦点()1,0F ，准线1:-=y l ，连AF 、BF ，设A 、B 、M 到准线l 的距离分别为1d 、2d 、d 则322221=≥+=+=AB BF AF d d d ， ∴点M 到x 轴的最近距离为2．8.2解：(1)9或964解析：当焦点在ｘ轴上时，3181=-m ，得9=m ；当焦点在ｙ轴上时，3181=-m ，得964=m ． (2) 3171--或 解析：当焦点在x 轴上时，7)28(2=+++n n ，得1-=n ；当焦点在y 轴上时，7)2()82(=--+--n n ，得317-=n ．(3) )161,0(a 解析：抛物线方程的标准式为y ax 412=．8.3解：(1)（基本轨迹法） 设)0,5(,)0,5(21F F -，动圆半径为R ，则31+=R PF ，12+=R PF ，221=-PF PF ，由双曲线定义，点P 的轨迹是以1F 、2F 为焦点的双曲线的一支，1=a ，24,52==b c ，它的轨迹方程是)1(12422≥=-y x y ． (2) (转移法) 设),(),,(00y x C y x G ，则3,300yy x x ==，即y y x x 3,300==，代入椭圆得1144)3(324)3(22=+y x ，又三角形中三点不共线，0≠∴x , 所以重心G 的轨迹方程是)0(1163622≠=+x y x ．8.4 解： )0,2()0,2(21F F -，当x PQ ⊥轴时, )3,2(,)3,2(-Q P ，12=S ； 当AB 与x 轴不垂直时, 设直线)0)(2(:≠-=k x k y PQ ,代入椭圆方程得0481616)43(2222=-+-+k x k x k ,设),(11y x P ,),(22y x Q , 则22212221434816,4316kk x x k k x x +-=+=+, 2222243)1(24431241k k k k k PQ ++=+++= , 点1F 到直线PQ 的距离 214kk d +=,由此得222222)43()1(484314821k k k k k k d PQ S ++=++== , 设t k =+243，其中3>t ，则232112t t S --=随t 的增大而增大，120<<S ， 所以PQ F 1∆面积S 的取值范围是(]12,0.(2)设直线2)1(:+-=x k y l ， 代入双曲线方程4422=-y x 得[]01)2(4)2(8)41(222=+-----k x k k x k ，[]0)543(161)2()41(16)2(6422222=+--=+--+-=∆k k k k k k ，得3192±-=k ， 双曲线的渐近线斜率为21±，如图，可知直线l 的斜率范围是)21,3192(---． 8.6解：)0,2(-F ,当x l ⊥轴时,)214,1(P ,)214,1(-Q ,不合． 设直线)1(:-=x k y l ，代入椭圆得0824)21(2222=-+-+k x k x k ,设),(11y x P ,),(22y x Q , 则 ,2142221kk x x +=+22212182k k x x +-=, 2212212212214))(1()1()1)(2()2)(2(k x x k x x k x x k x x FQ FP +++-++=--+++=⋅=2222222421)2(421)82)(1(k k k k k k k +++-++-+=02141122=+-k k ,得112±=k , 所以直线的方程为)1(112-±=x y ．9.1解：(1) 373)4242(433122=⋅⨯++=V ． (2)表面积ππππ425)41(4122=⋅++⋅+⋅=S ，体积ππ284)4161(31=⋅++=V ． 9.2解：(1)取AB 中点O ，连OC ，则AB PO ⊥，ABC PAB 面面⊥ ，ABC PO 面⊥∴， ABC PC PCO 与面就是∠∴所成的角，103010232tan 10232==∠==PCO OC PO ，，， 所以所求角的正切值为1030．。

专题03不等式易错点一：忽略不等式变号的前提条件（等式与不等式性质的应用）1．比较大小基本方法关系方法做差法与0比较做商法与1比较b a >0>-b a )0(1>>b a b a ，或)0(1<<b a b a ，b a =0=-b a )0(1≠=b baba <0=-b a )0(1><b a b a ，或)0(1<>b a ba ，2．．等式的性质（1）基本性质性质性质内容对称性ab b a a b b a >⇔<<⇔>；传递性c a c b b a c a c b b a <⇒<<>⇒>>，；，可加性cb c a b a >>+⇔>可乘性b ac c b a bc ac c b a <⇒<>>⇒>>00，；，同向可加性db c a d c c a +>+⇒>>，同向同正可乘性bdac d c b a >⇒>>>>00，可乘方性nn b a N n b a >⇒∈>>*0，类型1．应用不等式的基本性质，不能忽视其性质成立的条件，解题时要做到言必有据，特别提醒的是在解决有关不等式的判断题时，有时可用特殊值验证法，以提高解题的效率．类型2．比较数（式）的大小常用的方法有比较法、直接应用不等式的性质、基本不等式、利用函数的单调性．比较法又分为作差比较法和作商比较法．作差法比较大小的步骤是：（1）作差；（2）变形；（3）判断差式与0的大小；（4）下结论．作商比较大小（一般用来比较两个正数的大小）的步骤是：（1）作商；（2）变形；（3）判断商式与1的大小；（4）下结论．其中变形是关键，变形的方法主要有通分、因式分解和配方等，变形要彻底，要有利于0或1比较大小．作差法是比较两数（式）大小最为常用的方法，如果要比较的两数（式）均为正数，且是幂或者因式乘积的形式，也可考虑使用作商法．易错提醒：(1)一般数学结论都有前提，不等式性质也是如此．在运用不等式性质之前，一定要准确把握前提条件，一定要注意不可随意放宽其成立的前提条件．(2)不等式性质包括“充分条件(或者是必要条件)”和“充要条件”两种，前者一般是证明不等式的理论基础，后者一般是解不等式的理论基础．，b，，若a b>，则下列不等式成立的是（）易错点二：遗漏一元二次方法求解的约束条件（有关一元二次不等式求解集问题）解一元二次不等式的步骤：第一步：将二次项系数化为正数；第二步：解相应的一元二次方程；第三步：根据一元二次方程的根，结合不等号的方向画图；第四步：写出不等式的解集．容易出现的错误有：①未将二次项系数化正，对应错标准形式；②解方程出错；③结果未按要求写成集合．对含参的不等式，应对参数进行分类讨论具体模型解题方案：1、已知关于x 的不等式02>++c bx ax 的解集为)(n m ，（其中0>mn ），解关于x 的不等式02>++a bx cx ．由02>++c bx ax 的解集为)(n m ，，得:01)1(2>++c x b x a 的解集为)11(m n ，，即关于x 的不等式02>++a bx cx 的解集为11(mn ，．已知关于x 的不等式02>++c bx ax 的解集为)(n m ，，解关于x 的不等式02≤++a bx cx ．由02>++c bx ax 的解集为)(n m ，，得:011(2≤++c x b x a 的解集为)1[]1(∞+-∞，，m n 即关于x 的不等式02≤++a bx cx 的解集为)1[]1(∞+-∞，，mn ．2、已知关于x 的不等式02>++c bx ax 的解集为)(n m ，（其中0>>m n ），解关于x 的不等式02>+-a bx cx ．由02>++c bx ax 的解集为)(n m ，，得:01)1(2>+-c x b x a 的解集为11(n m --，即关于x 的不等式02>+-a bx cx 的解集为)11(nm --，．3．已知关于x 的不等式02>++c bx ax 的解集为)(n m ，，解关于x 的不等式02≤+-a bx cx ．由02>++c bx ax 的解集为)(n m ，，得:01)1(2≤+-c x b x a 的解集为)1[1(∞+---∞，，nm 即关于x 的不等式02≤+-a bx cx 的解集为)1[]1(∞+---∞，，nm ，以此类推．4、已知关于x 的一元二次不等式02>++c bx ax 的解集为R ，则一定满足⎩⎨⎧<∆>00a ；5、已知关于x 的一元二次不等式02>++c bx ax 的解集为φ，则一定满足⎩⎨⎧≤∆<00a ；6、已知关于x 的一元二次不等式02<++c bx ax 的解集为R ，则一定满足⎩⎨⎧<∆<00a ；7、已知关于x 的一元二次不等式02<++c bx ax 的解集为φ，则一定满足⎩⎨⎧≤∆>00a ．易错提醒：一元二次不等式一元二次不等式20(0)ax bx c a ++>≠，其中24b ac ∆=-，12,x x 是方程20(0)ax bx c a ++>≠的两个根，且12x x <（1）当0a >时，二次函数图象开口向上．（2）①若0∆>，解集为{}21|x x x x x ><或．(2)当0a <时，二次函数图象开口向下．①若0∆>，解集为{}12|x x x x <<②若0∆≤，解集为∅。

高中数学易错题举例分析高中数学中有很多题目，求解的思路不难，但解题时，对某些特别情况的议论，却很简单被忽视。

也就是在转变过程中，没有注意转变的等价性，会常常出现错误。

本文经过几个例子，分析致错原由，希望能对同学们的学习有所帮助。

增强思想的严实性训练。

●忽视等价性变形，以致错误。

x>0x +y>0x>1x +y>3y>0xy>0，但y>2与xy>2不等价。

【例 1】已知 f(x) =a x +x3 f (1)0, 3 f (2) 6, 求 f (3) 的范围。

b ，若3 a b0①错误会法由条件得32a b6②2②× 2－①6a15③①× 2－②得8b2④333③+④得103a b43,即10 f (3)43.33333x 错误会析采纳这类解法，忽视了这样一个事实：作为知足条件的函数 f ( x) ax，b 其值是同时受 a和b 限制的。

当a取最大（小）值时， b 不必定取最大（小）值，因此整个解题思路是错误的。

f (1) a b正确解法由题意有f ( 2)b,解得：2a2a1[ 2 f (2) f (1)], b2[ 2 f (1)f (2)],33f (3)3a b16f (2)5f (1).把 f (1) 和 f (2) 的范围代入得39916 f (3)37.33在本题中能够检查出解题思路错误，并给出正确解法，就表现了思想拥有反省性。

只有坚固地掌握基础知识，才能反省性地看问题。

●忽视隐含条件，以致结果错误。

【例 2】(1)设、是方程 x 22kx k 6 0 的两个实根，则 (1) 2(1) 2的最小值是( A )49(B)8(C) 18(D)不存在4思路分析 本例只有一个答案正确，设了3 个圈套，很简单受骗。

利用一元二次方程根与系数的关系易得：2k,k6,( 1) 2(1) 222 1 2 21( ) 2 22() 24( k3) 2 49 .44有的学生一看到49，常受选择答案（ A ）的迷惑，盲从附和。

数学必修一易错题、好题、难题前言：本人为衡水中学毕业生，高中三年记了很多错题本、积累本，高考之后不会再看了，但扔了可惜，所以现将当年积累的错题一点点整理出来，希望对各位学弟学妹有帮助。

如有错误，望告知。

⒈ 已知a ∈Z ，A={(x ,y ) | ax -y ≤3}且(2,1)∈A ，(1,-4)∉A ，则满足条件的a 的值为0或1或2. 解：∵(2,1)∈A ，∴2a -1≤3，∴a ≤2；∵(1,-4)∉A ，∴a +4>3，a ＞-1。

∵a ∈Z ，∴a 为0,1,2. ⒉ 已知集合A={x ∈R | ax 2-3x +2=0}.⑴若A=∅，求实数a 的取值范围；⑵若A 是单元素集，求a 得值及集合A ；⑶求集合P={a ∈R | a 使得A≠∅ }.解：⑴∵A=∅ ∴{a ≠0∆=9−8a <0，解得a >98. ⑵ ①当a =0时，-3x +2=0，解得x =23，∴A={23}.②{a ≠0∆=9−8a =0，解得a =89，∴A={43}. 综上所述，当a =0时，A={23}；当a =98时，A={43}.⑶由⑴可知，a ≤98.⒊ 已知集合A={x ∈R|mx 2−2x +3=0,m ∈R }，若A 重元素至多有一个，求m 的取值范围.解：①当m =0时，-2x +3=0，∴x =32. ②{m ≠0∆=4−12m ≤0，解得m ≥13. 综上所述，m 的取值范围为m ≥13或m =0. ⒋ 用列举法表示集合B={a 9−x ∈N|x ∈N}.解：B={1,3,9}.⒌ 设B={1,2}，A={x|x ⊆B }，则A 与B 的关系是 B ∈A .解析：∵x ⊆B ，∴x ={{1},{2},{1,2},∅}，∴B ∈A.⒍ 已知集合A={x|x 2−2x −3=0}，B={x|ax −1=0}，若B ⊆A ，则实数a 的值构成的集合是{-1,0,13}.解析：此题容易落掉B=∅的情况，当B=∅时，a =0.7 若{x|2x −a =0,a ∈N }⊆{x|−1<x <3}，则a 的所有取值组成的集合为{0,1,2,3,4,5}. 解析：x =a 2，∴-1<a 2<3，即-2<a <6，又∵a ∈N ，∴a =0，1,2,3,4,5.⒏ 设集合A={1,a,b }，B={a,a 2,ab }，且A=B ，实数a 的值为 -1 .解析：①{a 2=1ab =b，解得a =±1，∵a ≠1，∴a =-1，此时b =0. ②{a 2=b ab =1，此种情况不成立. ⒐ 已知集合A={x|0<x <3}，B={x|m <x <4−m }，且B ⊆A ，则实数m 满足的条件是 m ≥1.解析：当B=∅时，m ≥4-m ，m ≥2；当B ≠∅时{m ≥04−m ≤3m <4−m ，解得{m ≥0m ≥1m <2，综上所述，m ≥1.⒑ 设集合A={−1,1}，试用列举法写出下列集合.⑴ B={(x,y )|x,y ∈A } ⑵ C={x|x ⊆A }解：B={(−1,−1),(1,1),(−1,1),(1,−1)}. C={∅,{−1},{1},{(−1,1)}}.⒒ 已知三元素集合A={x,xy,x −y }，B={0,|x |,y }，且A=B ，求x 与y 的值.解：∵x ≠0，y ≠0，∴xy ≠0，∴x -y =0，∴{x =yx −y =0xy =|x|，解得x =y =±1. 当x =1时，A={1,1,0}（舍去）；当x =-1时，A={-1,1,0}，B={0,1,-1}.综上所述，x 与y 的值均为-1.⒓ A={x|x 2+4x =0}，B={x|x 2+2(a +1)x +a 2−1=0}.⑴ 若A ⊆B ，求a 的值； ⑵ 若B ⊆A ，求a 的值.解：A={0,-4}.⑴ ∵A ⊆B ，∴B={0,-4}，∴{−4=−2(a +1)0=a 2−1，解得a =1. ⑵ ∵B ⊆A ，∴①若B=∅，∆=8a +8<0，∴a <-1.②若B 为单元素集，即B={0}或{-4}，∴∆=8a +8=0，a =-1，∴x 2=0，x =0，B={0}.③若A=B ，则a =1.综上所述，a ≤-1或a =1.⒔ 已知集合A={x|−2≤x ≤5}，非空集合B={x|m +1≤x ≤2m −1}，且B ⊆A ，求m 的取值集合.解：∵B ⊆A 且B 为非空集合，∴{m +1≥−22m −1≤5m +1≤2m −1，解得2≤m ≤3，即m 的取值集合为{m|2≤m ≤3}.⒕ 已知集合A={x|ax 2−3x −4=0,x ∈R }.⑴若A 中有两个元素，求实数a 的取值范围；⑵若A 中至多有一个元素，求实数a 的取值范围.解：⑴∵A 中有两个元素，∴{a ≠0∆=9+16a >0，∴a >-916且a ≠0. ⑵当a =0时，-3x -4=0，∴x =-43；当a ≠0时，∆=9+16a ≤0，∴a ≤-916.综上所述，a 的取值范围为a ≤-916或a =0.⒖ 设集合A={2, a }，B={a 2-2, 2}，若A=B ，则实数a 的取值范围为{-1}.解析：∵A=B ，∴a 2-2=a ，∴a 1=-1，a 2=2. ∵a ≠2，∴a =-1.⒗ 已知A ⊆B ，其中A={x|ax −1=0,a ∈R }，若A=B ，则实数a 的取值集合为{-1,0,1}. 解析：因为A ⊆B ，∴①当A=∅时，a =0；②当A ≠∅时，a =±1. ∴a 为{-1,0,1}.⒘ 已知全集U=R ，A={x|−2≤x ≤3}，B={x|x −a >0}，A ⊆B ，求a 的取值范围. 解：a <-2.⒙ 设全集I={(x,y )|x,y ∈R }，集合M={(x,y )|y−3x−2=1}，N={(x,y )|y ≠x +1}，那么(∁I M )∩(∁I N)等于{(2,3)}.解析：M={(x,y )|y =x +1,x ≠2,y ≠3}，∴M ∪ N={(x,y )|x ≠2,y ≠3}，∴∁I (M ∪N )={(2,3)}.⒚ 设数集M={x|m ≤x ≤m +34}，N={x|n −13≤x ≤n}，且M ，N 都是集合{x|0≤x ≤1}的子集，如果把b -a 叫做集合{x|a ≤x ≤b }的“长度”，那么集合M ∩N 的“长度”的最小值是（112）. 解析：∵M ⊆{x|0≤x ≤1}，∴0≤m ≤34，∵N ⊆{x|0≤x ≤1}，∴23≤n ≤1，∴M ∩N={x|23≤x ≤34}，∴长度为112.⒛ 若{x ∈R|x 2+2(a +1)x +a 2−1=0}⊆{x|x 2=0}，则实数a 的取值范围是a ≤−1. 解析：① ∆=4(a 2+2a +1)-4(a 2-1)<0，∴a <-1；② ∆=4(a 2+2a +1)-4(a 2-1)=0，∴a =-1.综上所述，a ≤-1.。