当前位置：文档之家 › 可逆过程与可逆过程体积功

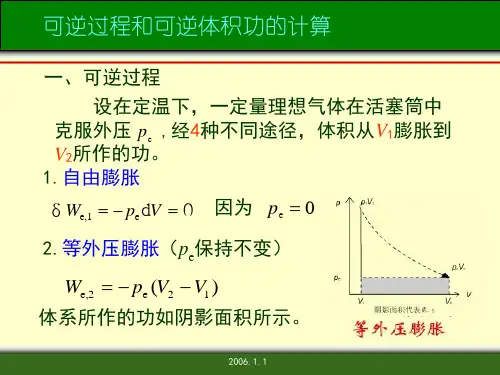
可逆过程与可逆过程体积功

  • 格式：ppt
  • 大小：1.22 MB
  • 文档页数：32

下载文档原格式

  / 32

合集下载

14-可逆过程与可逆功解析

14-可逆过程与可逆功解析

上一内容
下一内容 返回
回主目录
功与过程
上一内容
下一内容
回主目录
返回
功与过程
2.多次等外压压缩 第一步：用 p" 的压力将体系从 V2 压缩到V " ； 第二步：用 p' 的压力将体系从V " 压缩到V ' ； 第三步：用 p1 的压力将体系从 V ' 压缩到 V1 。
W p (V V2 )
pV K1
TV 1 K2
p1 T K3
式中， K1, K2 , K 3 均为常数， C p / CV 。

上一内容
下一内容
回主目录
返回
可逆体积功的计算
三、可逆体积功的计算 1、理想气体恒温可逆过程
V2 P W nRT ln nRT ln 1 V1 P2
We,3 p '(V 'V1 ) p "(V " V ') p2 (V2 V ")
所作的功等于3次作功的加和。
可见，外压差距越小，膨胀 次数越多，做的功也越多。
上一内容
下一内容
2006.1.1 回主目录
返回
2006.1.1
功与过程
上一内容
下一内容
2006.1.1 回主目录
2、理想气体绝热可逆过程
W U nCV ,m (T2 T1 )
上一内容
下一内容
回主目录
返回
绝热过程
绝热过程的功
在绝热过程中，体系与环境间无热的交换，但可 以有功的交换。根据热力学第一定律：
dU Q W
=W
（因为Q 0）
这时，若系统对外作功，热力学能下降，体系温
2-9可逆过程与可逆体积功

2-9可逆过程与可逆体积功


2013-7-14
3
例1, 3mol理想气体于恒温298.15K条件下由始态 V1 = 20.0dm3 可逆膨胀到末态V2 = 50.0dm3 . 求始, 末态气体的压力p1 , p2 以及 膨胀过程的可逆功Wr .
n = 3 mol p1 = V1 = 20dm3 T1 = 298.15K 恒温可逆 n = 3 mol p2 = V2 = 50dm3 T2 = 298.15K
2. 可逆体积功（reversible volume work ）
W
V2
V1
pd V
pamb p
(1). 理想气体恒温可逆过程
WT ,r pdV nRT dV V1 V1 V
V2 V2
WT ,r
V1 p2 nRTln nRTln V2 p1
nRT V p
2013-7-14
p2 Wr nRT ln p1
4
{ 3 8.314 298.15 ln(20.0 / 50.0 )}J 6814J
(2). 理想气体绝热可逆过程
Wa,r pdV
V2 V1
绝热与恒温的区别？
2013-7-14
5
①. 理想气体绝热可逆过程方程式
T2 T1 V1 V 2
②. 理想气体绝热可逆体积功 不论可逆与否, 绝热过程的功总可以用 W = U 来进行计算 , 这种方法更加简便.
Wa,r U nCV ,m (T2 T2 )
2013-7-14
7
例36 1 mol氧气由0℃, 106Pa，经过（1）绝热可逆膨胀；（2） 对抗恒定外压Psu= 105Pa绝热不可逆膨胀，使气体最后压力为 105Pa，求此两种情况的最后温度及系统对环境所作的功。 解（1）绝热可逆膨胀 绝热可逆膨胀 1molO2 p1 = 106Pa T1 = 273.15K
2.10可逆过程与可逆体积功

2.10可逆过程与可逆体积功


气体可逆膨胀压缩过程
以理想气体恒温膨胀压缩过程为例， 以理想气体恒温膨胀压缩过程为例，将盛 有一定量某理想气体的带活塞的气缸与恒温热 源接触， 源接触，以使平衡时系统的温度与热源的温度 相等。 相等。 系统始态为a压力为 末态为z压力为 压力为p 系统始态为 压力为pa；末态为 压力为 z， 压力为 pz＝1/5pa 。
理想气体绝热可逆功
Wa,r = ∆U = ∫T nCV ,mdT = nCV ,m (T2 − T1 )
T2
1
T2根据绝热可逆过程方程式求得。 根据绝热可逆过程方程式求得。 或
Wa,r = ∫ − pamb dV = ∫ − pdV = ∫
V1 V1
V2
V2
V2
V1
p1V1γ − γ dV V
p1V1γ 1 1 = γ −1 − γ −1 V1 γ − 1 V2
3)绝热恒外压膨胀 : ∆U = W 绝热恒外压膨胀 绝热 nCV,m (T2 −T1) = －p2(V2 −V1) = －p2V2＋p2V1
3 p2 n R(T2 −T ) = nRT1 − nRT2 1 2 p1 3 p2 T2 = 174.8K (T2 −T ) = T −T2 1 1 2 p1 ∆U= nCV,m(T2 −T1) = −5.40×103J
p1V1γ − γ dV V
• P95,39 解：设计变化途径如下： 设计变化途径如下：
n = 5mol T2 = 300K p2 = 50kPa V2
n = 5mol T1 = 300K p1 = 200kPa V1
Байду номын сангаас恒温 可逆
绝热 可逆
n = 5mol T3 p3 = 200kPa V3
§1.0-§1.3 热力学基本概念-热与功

§1.0-§1.3 热力学基本概念-热与功

兼有气体及液体双重特性； 超临界流体特性 体积质量接近液体； 粘度接近气体； 扩散系数比液体大约10倍。
表1.2 一些物质的临界参量
物 He H2 N2 O2 H2O CH4 C2 H 4 C6H6 C2H5 OH 质 Tc/K 5.26 33.3 126.2 154.4 647.4 190.7 283.1 562.6 516.3 pc/MPa 0.229 1.30 3.39 5.04 22.12 4.64 5.12 4.92 6.38 Vm,c/10-6m3·mol-1 58 65 90 74 56 99 124 260 167
相变化过程与饱和蒸气压 相变化过程：一定条件下聚集态的变化过程。
气体 (T,p) 汽化 液体 液化 凝固 熔化 (T,p) 固体(α) (T,p) 升华 凝华 晶型转化 (T,p) 固体(β)
饱和蒸气压：
在一定温度下，当液（或 固）体与其蒸汽达成液（或 固）汽两相平衡时，汽相的压 力称为该液（或固）体在该温 度下的饱和蒸气压。
焦耳实验
或: 整个系统(双球） dV＝0
气体 真空 图1-1气体向真空膨胀 （自由膨胀）
(3) 对抗恒定外压过程
p1,V1 Psu p2,V2 Psu
T1
T1
膨胀过程的功：
W = − ∫V psu dV
V2
1
= −psu(V2 −V) 1
压缩过程的功：
p2,V2 Psu
T1p1,V1Psu NhomakorabeaT1
W = − ∫V psu dV
第一节 热力学基本概念
0.系统和环境
系统: 热力学研究的对象(微粒组成的宏观集合体)。 环境: 与系统通过物理界面(或假想的界面)相 隔开并与系统密切相关的周围部分。
第一章 热力学第一定律

第一章 热力学第一定律


1.2热力学基本概念
热和功
Closed system (t1)
Surroundings (t2)
热（heat）：封闭体系与环境 之间因温差而传递的能量 > 0 吸热 规定：Q < 0 放热 功（work）：封闭体系与环境之 间除热以外传递的其他一切能量 > 0 环境对体系做功 规定：W < 0 体系对环境做功
1、研究物质的宏观性质（
macroscopic properties ）。
2、只需知道系统的起始状态和最终状态以及过程进
行的外界条件无需知道过程机理及物质结构。 3、研究的变量没有时间概念，不涉及速率问题。
局限性
不涉及微观结构（Microscopic）和反应 机制（ Mechanism）。
Company Logo
摩尔气体常数：
8.314 J / K ·mol
对于多组分均相系统的状态函数还与其组 成成分有关，即 V = f (p,T,n1, n2 ,n3……)
Company Logo

注意：热力学定律并不能导出 具体系统的状态方程，它必须 由实验来确定。
Company Logo
1
50
100

1.2热力学基本概念 state B path 2
path 1 state A
始态至终态的一切变化——过程（process） 具体步骤 —— 途径（path）
Company Logo

1.2热力学基本概念
常见的变化过程有：
1.2热力学基本概念
状态函数具有下述特性：
1） 状态函数是状态的单值函数。 2）状态函数的改变量只取决于系统的始态和终态， 与变化的途径无关。 3）状态函数的微小变化，在数学上是全微分
2-10可逆过程和可逆体积功

2-10可逆过程和可逆体积功


•多次等外压膨胀
（3）.外压比内压小一个无穷小的值
外压相当于一堆沙子，每次取一粒，这样的膨胀过程是 无限缓慢的，每一步都接近于平衡态。所作的功：
P终 p始

一粒粒取走砂粒 (剩余砂粒相当前述一 个重物)
(iii)

即 TV 1 常 ： 数
结 pg状 方 有 合 态 程
：
pV 常 数
1
Tp

常 数
pV c

b、理想气体绝热可逆体积功
由 热 逆 程 绝 可 方 ：
V2 V1
pV p1V1
W的定义式


Wr pdV p1V1



V2
V1
V dV
V2
V2
V2
（2）理想气体绝热可逆体积功
a、 理想气体绝热可逆过程方程式
d U δWr δ Qr 0 nRT 理想气体 nCV,m d T p d V dV V
对 热 逆 程 绝 可 过 ，
CV,m dT dV R T V
pg :C p,m CV, m R γ C p,m CV, m
W p (V V 1)
' '
p终 p始 p1 P1
p'' (V '' V ' )
p2 (V2 V '' )
(ii)
P始,V始 T
V1
1 P 1,V 1 T
p2 V2
2
P2
p终V3
3 P终,V终
P2,V2 T
可逆过程与可逆过程体积功

可逆过程与可逆过程体积功


T2
= U
n CV ,mdT
T1
T2
= H
n C p,mdT
T1
7
单
纯pVT变
化
—
—
显
热QQVp
Q......... 相
变
—
—
相
变
焓
（
潜
热
）可不
逆 可
相变 逆相
变
化
学
反
应—
—
化
学
反
应
热恒恒
压 容
反 反
应 应
热 热
8
§ 2.5 相变过程热的计算
1. 相及相变
(1)相的定义: 系统内性质完全相同且均匀的部分称为相。 (2)相变:物质从一相转移至另外一相,称为相变。 (3)常见相变:
ln
p2 p1
4. 理想气体绝热可逆过程
T2 T1
V2 V1
1
1 1
T2 T1
p2 p1
4 p1V1 p2V2
5. 绝热可逆过程体积功的计算
方法一：
Wr
pdV
V2 nRT dV V1 V
V2 p0V0
V V1
dV
p0V0
1 V2 V V1
dV p0V0
1
(V21 V11 )
Q Qp H 40.63kJ
28
(2) 100℃下向真空蒸发
H2O(l) T1 373.15K p1
p外0 H
H2O(g) T2 373.15K p2 101.325k Pa
H1
H2O(l) T 373.15K
H 2
p 101.325k Pa
第1章可逆过程

第1章可逆过程

0kJ 18.24kJ 18.24kJ
Q U W
0 18.24kJ 18.24kJ
，
11
解法二:
因为
PV 1 1 nRT 1
3 3
202.65 pa 10 10 m PV 1 1 243.745K 所以 T1 1 1 nR 1mol 8.314 J K mol 3 3 2026.5 p 10 10 m PV a 同理 T2 2 2 2437.45K 1 1 nR 1mol 8.314 J K mol
V2
1
V2
V1
QP H n C P,m dT nCP,m T2 T1
T2
U n CV ,m dT nCV ,m T2 T1
T2 T1
T1
9
例2-2 1mol的理想气体H2(g)由202.65kPa、10dm3等容升温， 压力增大到2026.5kPa,再等压压缩至体积为1dm3。 求整个过程的 Q、W、U和H
1
V2
QV U n CV ,m dT nCV ,m T2 T1
T2 T1
H n C P,m dT nCP,m T2 T1
T2 T1
3．等压过程
W pe dV pdV p V2 V1 nRT2 T1 V
一、热力学可逆过程的特点
1.可逆过程进行时，系统状态变化的动力与阻力相差无限小， 所以在恒温条件下，系统可逆膨胀时对环境所作的功最大， 系统可逆压缩时从环境得到的功最小。 2.可逆过程进行时，系统与环境始终无限接近于平衡态；或 者说，可逆过程是由一系列连续的、渐变的平衡态所构成。 因此，可逆即意味着平衡。 3.若变化循原过程的逆向进行，系统和环境可同时恢复到原 态。同时复原后，系统与环境之间没有热和功的交换。 4.可逆过程变化无限缓慢，完成任一有限量变化所需时间无 限长。
热力学第一定律复习

热力学第一定律复习

11/46 11/46
所以上述两过程 W≈0
20112011-4-2
祝大家学习愉快，天天进步！ 祝大家学习愉快，天天进步！
3、相变化
（2）有气体参加的过程 例:蒸发 B（l）→ B（g）
定温、定压，W’ =0 时 可逆相变 定温、定压，
Q p =∆ g H l
W = − p∆V = − p (Vg − Vl ) ≈ − pVg ≈ −nRT
20112011-4-2
祝大家学习愉快，天天进步！ 祝大家学习愉快，天天进步！
13/46 13/46
3、相变化
可逆相变
气液间可逆相变（ 气液间可逆相变（恒T、P）P是液体在T时的饱和蒸汽压。 可逆相变 是液体在T时的饱和蒸汽压。 气固间可逆相变 可逆相变（ 是固体在T时的饱和蒸汽压。 气固间可逆相变（恒T、P）P是固体在T时的饱和蒸汽压。 固液间可逆相变 可逆相变（ 是固体在P时的熔点。 固液间可逆相变（恒T、P）T是固体在P时的熔点。
∆U = Q + W ≈∆ g H − nRT l
[一般在大气压及其平衡温度下的相变（可逆相变） 一般在大气压及其平衡温度下的相变（可逆相变） 焓数据可查文献，是基础热数据， 焓数据可查文献，是基础热数据，其与压力关系不 因此不标明压力] 大，因此不标明压力]
20112011-4-2 祝大家学习愉快，天天进步！ 祝大家学习愉快，天天进步！ 12/46 12/46
由热力学稳定单质生 （6） 标准摩尔生成焓：一定温度下由热力学稳定单质生 ） 标准摩尔生成焓：一定温度下由热力学稳定单质 的物质B的标准摩尔反应焓 的物质 的标准摩尔反应焓， 成化学计量数 νB=1的物质 的标准摩尔反应焓，称为物质 B在该温度下的标准摩尔生成焓。 ∆f H m ( B )表示 在该温度下的标准摩尔生成焓 在该温度下的标准摩尔生成焓。 没有规定温度， 时的数据有表可查。 1）没有规定温度，一般298.15 K时的数据有表可查。 3）由定义可知：稳定态单质的 ∆f Hm ( B) = 0 稳定态单质的 （6） 标准摩尔燃烧焓:一定 标准摩尔燃烧焓:一定温度下， 1mol物质 B 与 氧气进行完全燃烧反应，生成规定的燃烧产物时的 标准摩尔反应焓，称为B在该温度下的标准摩尔燃烧 焓。 ∆ Hm ( B) 表示.单位：J mol-1 c
(2)-01章-热力学第一定律(可逆过程,体积功,焓,热容)

(2)-01章-热力学第一定律(可逆过程,体积功,焓,热容)

物理化学电子教案—第一章
热力学第一定律及其应用
环境 surroundings
无物质交换 封闭系统
Closed system
U Q W
有能量交换
上一内容 下一内容 回主目录
返回
2020/3/7
热力学第一定律
Joule（焦耳）和 Mayer（迈耶尔)自1840年 起，历经20多年，用各种实验求证热和功的转 换关系，得到的结果是一致的。
也可以表述为：第一类永动机是不可能制成的
第一类永动机（first kind of perpetual motion machine):一种既不靠 外界提供能量，本身也不减少能量，却可以不断对外作功的机器 称为第一类永动机，它显然与能量守恒定律矛盾。
热力学第一定律是人类经验的总结，事实证明违背该定 律的实验都将以失败告终，这足以证明该定律的正确性。
U U2 U1 QW 对于微小变化 dU Q W
热力学能的单位： J
热力学能是状态函数，用符号U表示，它的 绝对值尚无法测定，只能求出它的变化值。
上一内容 下一内容 回主目录
返回
2020/3/7
热力学第一定律的文字表述
热力学第一定律是能量守恒与转化定律在热现 象领域内所具有的特殊形式，说明热力学能、热和 功之间可以相互转化，但总的能量不变。
自然界的一切物质都具有能量，能量有各 种不同形式，能够从一种形式转化为另一种形 式，但在转化过程中，能量的总值不变。
上一内容 下一内容 回主目录
返回
2020/3/7
热力学能
系统总能量通常有三部分组成：
（1）系统整体运动的动能 （2）系统在外力场中的位能 （3）热力学能，也称为内能 热力学中一般只考虑静止的系统，无整体运动， 不考虑外力场的作用，所以只注意热力学能
体积功与可逆过程

体积功与可逆过程

Cp，m
晶Ⅱ 晶Ⅰ
液体
气体
T转晶
T熔
T沸
T
第四节 可逆过程与体积功
一、体 积 功
• pe = 外压
• A= 截面积
pe
• dl = 活塞移动距离
• dV = Adl = 体积的变化 • W = -F dl = -pe Adl
W = -pedV
dl
Gas 体系
A
对于宏观过程
W
V2 V1
pedV
二、不同过程的体积功
三、可逆过程
将准静态膨胀与压缩两图及（1）与（2）式相比 较，显然，准静态膨胀过程所作之功W4与准静态压缩 过程所作之功W ’3，大小相等，符号相反。在环境中没 有功的得失。
由 于 系 统 复 原 ， U=0 ， 根 据 热 力 学 第 一 定 律
U=Q+W，故Q＝-W，所以在环境中也无热的得失。
一定量的气体从始态体积V1膨胀到终态V2, 若过 程不同，则所作的功就不相同。
设在定温下，一定量理想气体在活塞筒中克服外 压 ,经几种不同途径，体积从V1膨胀到V2所作的功。
自由膨胀（free expansion） 外压为零的膨胀过程。此时pe =0，所以
W1
V2 V1
pedV
0
二、不同过程的体积功
二、不同过程的体积功
若采取与（2）、（3）、（4）过程相反的步骤 ，将膨胀后的气体压缩到初始的状态，同理，由于压 缩过程不同，作的功亦不相同。
4．恒定外压p1下压缩过程 在恒定外压p1下将气体从V2压缩到V1，环境所做功为 W1’= -p1(V1－V2) 环境对系统做功的值相当于图中的阴影面积。
p
亦即当系统回复到原态时，环境也回复。

物理化学知识点归纳

热力学第一定律△U=Q+W 或dU=ΔQ+δW=δQ-p amb dV+δW` 体积功δW=-p amb dV （1）气体向真空膨胀时体积功所的计算W=0 （2）恒外压过程体积功W=p amb （V 1-V 2）=-p amb △V （3）对于理想气体恒压变温过程W=-p △V=-nR △T （4）可逆过程体积功W r =⎰21p V V dV (5)理想气体恒温可逆过程体积功W r =⎰21p V V dV =-nRTln(V 1/V 2)=-nRTln(p 1/p 2)(6)可逆相变体积功W=-pdV焓Hdef U + p V △H=△U+△(pV) △H=⎰21,T T m p dT nC此式适用于理想气体单纯p VT 变化的一切过程 内能(1)△U=Qv△ U=⎰21,v T T m dT nC =）（12,v T -T m nC 摩尔定容热容C V ，m△ C V ，m =C V /n=(TU mаа)V (封闭系统，恒容，W 非=0)(3)摩尔定压热容C p,m C p,m ==n p C P⎪⎭⎫ ⎝⎛T H m аа （封闭系统，恒压，W 非=0）(4) C p, m 与 C V ，m 的关系系统为理想气体，则有C p, m —C V ，m =R 系统为凝聚物质，则有C p, m —C V ，m ≈0（5）热容与温度的关系，通常可以表示成如下的经验式 C p, m =a+bT+cT2或C p, m =a+b`T+c`T -2式中a 、b 、c 、b`及c`对指定气体皆为常数，使用这些公式时，要注意所适用的温度范围。

（6）平均摩尔定压热容Cp,mCp,m=⎰21,T T m p dT nC (T 2-T 1)四、理想气体可逆绝热过程方程,m2121(/)(/)1V C R T T V V =,m2121(/)(/)1p C RT T p p -= 1)/)(/(1212=r V V p pγγ2211V p V p =ξ=△n B /v BνB 为B 的反应计算数，其量纲为1。

2-10 可逆过程与可逆体积功


恒温可逆
n p2, V2, T
WT,r
V2 V1
pdV
V2 V1
nRT dV V
nRT ln V2 nRT ln V1
V1
V2
nRT ln p2 p1
U = 0 ， H = 0 ，Q = W
（2）理想气体的绝热可逆体积功
理想气体 可逆过程
dU n CV ,m dT
||绝热过程
W p dV nRT dV
∵ΔU = W ∴ nCV,m(T2'-T1)= -pamb(V2'-V1) = -p2 (nRT2'/p2 - nRT1/p1)
解：(1) 绝热可逆膨胀
T2 T1
p2 p1
R/Cp,m
T2 = 143K
n = 4.41 mol
Q=0
W = ΔU = nCV,m(T2-T1) = -12070J
末态 T，p0, 3V0
沿3条途径实现：
(a) 将两堆细砂一次拿掉： p
3p0, V0 始态
a
p0
Wa
p0 3V0 V0
V0
2p0V0
2/ 3RT
3p0V0 = RT
p0, 3V0 末态
3V0 V
(b)将两堆细砂分两次拿掉：
T, 3p0, V0
pamb= 2p0 Ⅰ
T, 2p0, 1.5V0
pamb= p0 Ⅱ
答案：C。节流膨胀过程恒焓绝热且压力降低。
詹姆斯·普雷斯科特·焦耳
（JamesPrescottJoule；1818年12月24日－ 1889年10月11日）
英国物理学家，出生于曼彻斯特近郊的沙弗 特（Salford）。由于他在热学、热力学和电方 面的贡献，皇家学会授予他最高荣誉科普利奖 章（CopleyMedal）。后人为了纪念他，把能量 或功的单位命名为“焦耳”，简称“焦”；并 用焦耳姓氏的第一个字母“J”来标记热量。

热力学第一定律2.5,2.6,2.7


二、 理想气体的 U
和 H 的计算
设理想气体的热力学能是 T ,V 的函数
U U (T ,V )
从Joule实验得 所以 同理
U U dU dT dV T V V T
U 0 V T
U dU dT CV dT T V
H H (T , p)
H H dH dp C p dT dT T p p T
对于理想气体，在等容不做非膨胀功的条件下
U QV CV dT
对于理想气体，在等压不做非膨胀功的条件下
H Q p C p dT
(封闭系统、理想气体、恒温可逆)
二、理想气体绝热可逆过程
1.绝热过程的特征 绝热Q＝0， 无非体积功Wf=0, （1）则
W U W dU
（2）绝热膨胀过程，V增大，W＜0，U减小，T降低 绝热压缩过程，V减小，W＞0，U增加，T升高 即绝热过程为变温过程
二、理想气体绝热过程的功和过程方程式
(A)
C p CV nR
CV
称为热容比
nR C p CV 1 CV CV
代入（A）式得
dT dV ( 1) 0 T V
绝热过程的功和过程方程式
dT dV ( 1) 0 T V 对上式积分得 ln T ( 1) ln V 常数 TV 1 K1 或写作 pV 因为 T 代入上式得 pV K2 nR
QV
U dT T V
CV , m
CV U m ( )V n T
(4)Cp、CV为状态函数
二．摩尔定压热容Cp,m与T的关系

标准摩尔定压热容： 是物质在标准压力100kPa下的摩尔定压热容，记为

热力学第一定律2-4

W1
V2 V1
p2＝0.5atm
p外 0
p外 dV p外 V 0
2、恒外压 p 外 0 .5 atm 膨胀
W2
V2
V1
p 外 d V p 外 V 2 V1
nRT nRT p外 p1 p2

1 1 0 . 5 1 8 . 314 273 . 15 1135 J 0 .5 1
V1
p系d V
S (曲线下面积）
环境所作 最小功值
V1 V2
p2
V
结 论
1、恒温压缩过程，环境对系统多次压缩比一次 压缩作功少，经过无数次压缩过程，环境对 系统做功最小。
2、一次、二次的膨胀、压缩过程， W 压缩 W 膨胀 循环过程： U 0; W 0; Q 0 即一次、二次膨胀、压缩后，系统复原，而环境
S1
V1
V2
二次压缩恒外压 p 外 0 . 75 atm 再 p 外 1atm
p
p1
W 2 p (V V 2 ) p1 (V1 V )
p`
p2
S1 S 2
'
S2
S
' 1
V1
V`
V2
V
气体经过无数次压缩
p外 p系 d p
p
p1
W

V2
§2−4
一、体积功与过程
体积功与可逆过程
问题
功是过程函数，与过程有关。始态、终态一定时， 过程功有无最大值？即什么过程系统能对环境做最大功？ 什么过程环境对系统做功最小？ 以恒温膨胀过程为例：
例：

可逆过程与可逆过程体积功

水的vapHm=40.63kJ·mol-１
H2O(g),2mol T1 283.15K p1 85k Pa
H1
H2O(g),2mol T2 373.15K p2 101.325k Pa
H
H 2
25
H2O(l),2mol T1 283.15K p1 85k Pa
H1

n
C dT T2
T1 p,m(l )
H3
T1 T2
nC
p,m
(
g
)dT
H2O(l) T2 373.15K p2 101.325k Pa
H 2
nvapHm ( 100C )
H2O(g) T2 373.15K p2 101.325k Pa
H H1 H2 H3
n H2O (s) T1 =253.15K
H1
H3
n H2O ( l ) T2=273.15K
n m 55.56mol M
H2 n H2O ( s ) T2=273.15K
H1
T2nC
T1
p
,m(
l
)dT

83.687k J
H2 nsl H m (0C ) n(ls H m ) 333.327kJ
2. 相变分类
(1)可逆相变：在指定温度及该温度对应的平衡压力下所发 生的相变，叫可逆相变。 例：
H 2O(l ) 100C 101.325k Pa
H2O(g) 可逆相变条件：
100C
dp=0, dT=0 , p =f(T)
101.325k Pa
H 2O(l ) 25C 3.167k Pa
H 2O(g ) 25C

物理化学重要概念公式总结

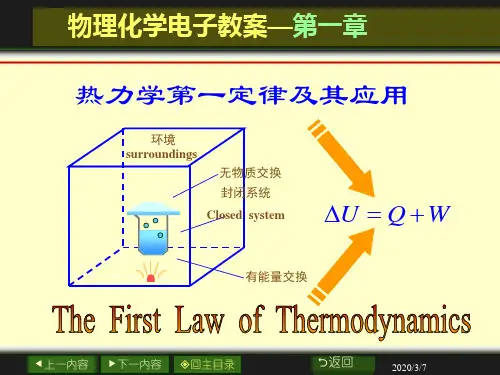
第一章 热力学第一定律一、基本概念系统与环境，状态与状态函数，广度性质与强度性质，过程与途径，热与功，内能与焓。

二、基本定律热力学第一定律：ΔU =Q +W 。

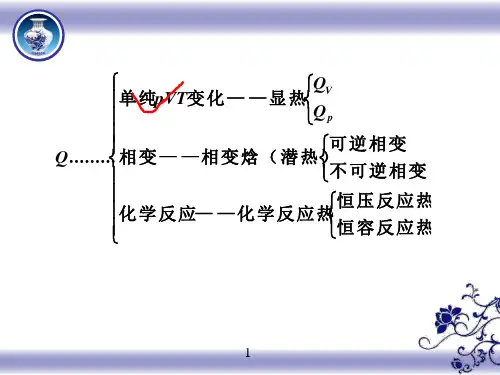
焦耳实验：ΔU =f (T ) ; ΔH =f (T )三、基本关系式1、体积功的计算 δW = －p e d V恒外压过程：W = －p e ΔV可逆过程： W =nRT 1221ln ln p p nRT V V =2、热效应、焓等容热：Q V =ΔU （封闭系统不作其他功）等压热：Q p =ΔH （封闭系统不作其他功）焓的定义：H =U +pV ; d H =d U +d(pV )焓与温度的关系：ΔH =⎰21d p T T T C3、等压热容与等容热容 热容定义：V V )(T U C ∂∂=；p p )(T HC ∂∂=定压热容与定容热容的关系：nR C C =-V p热容与温度的关系：C p =a +bT +c’T 2四、第一定律的应用1、理想气体状态变化等温过程：ΔU =0 ; ΔH =0 ; W =－Q =⎰-p e d V 等容过程：W =0 ; Q =ΔU =⎰T C d V ; ΔH =⎰T C d p 等压过程：W =－p e ΔV ; Q =ΔH =⎰T C d p; ΔU =⎰T C d V可逆绝热过程：Q =0 ; 利用p 1V 1γ=p 2V 2γ求出T 2,W =ΔU =⎰T C d V ;ΔH =⎰T C d p不可逆绝热过程：Q =0 ;利用C V (T 2-T 1)=－p e (V 2-V 1)求出T 2,W =ΔU =⎰T C d V ;ΔH =⎰T C d p2、相变化可逆相变化：ΔH =Q =n Δ＿H ；Ｗ＝－p (V 2-V 1)=－pV g =－nRT ; ΔU =Q +W3、热化学物质的标准态；热化学方程式；盖斯定律；标准摩尔生成焓。

摩尔反应热的求算：)298,()298(B H H m f B mr θθν∆=∆∑ 反应热与温度的关系—基尔霍夫定律：)(])([,p B C T H m p BB m r ∑=∂∆∂ν。

  1. 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
  2. 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
  3. 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

25
H 2O(g),2mol T1 283.15K p1 85kPa
H 1

H
H 2O(l),2mol T1 283.15K p1 85kPa
H 3
H 2O(g),2mol T2 373.15K p2 101.325kPa
T2
H2 T2 373.15K
QV n CV ,m dT
T1 T2
CV ,m
1 QV U m n dT T V
封闭系统，dV=0,W ’=0,单纯pVT变化 *对理想气体：W ’=0，单纯pVT变化 恒容过程 *对液体和固体： =
U n CV , m d T
T1
T2
非恒容过程
1. 相及相变
(1)相的定义: 系统内性质完全相同且均匀的部分称为相。 (2)相变:物质从一相转移至另外一相,称为相变。
(3)常见相变:
气相 晶型 转变 (trs)
固相
固相
熔化(fus) 凝固
9
液相
2. 相变分类
(1)可逆相变：在指定温度及该温度对应的平衡压力下所发 生的相变，叫可逆相变。 例：
H 2 O( l ) 100C 101.325kPa H 2 O( l ) 25C 3.167kPa
W =0
ΔU
ΔH
=0 =0 =0 =0 =0 =0
6
=0
=0
=0
=0
=0
H 2 O( l ) T1 298.15K
p1 3.167kPa
相变 过程
H 2 O( g ) T2 373.15K p2 101.325kPa
T2
U
T2
=
nC
V ,m
dT
H
T1
=
nC
p ,m
vap H m(T2 ) vap H m(T1 ) C p ,m(g) C p ,m(l)dT T1
T2
16
通式：


T2 T1
H m(T2 ) H m(T1 ) C p,mdT
由T1的相变焓计算T2的相变焓
C p ,m C p ,m() C p ,m()
n vap H m ( 25 C )

H
H 2O(g) T1 298.15K p1 3.167kPa
H 3
H 1 nT C p,m ( l )dT

T1
T2
nC p,m ( g )dT
H 2O(l) T2 373.15K p2 101.325kPa
nvap H m ( 100C )
H2
n H2O ( s ) T2=273.15K
Q = Qp= H = -291.43kJ H = U+ (pV) U H = -291.43kJ W= - p外V 0
24
(pV) = pV 0
例9 求2mol水蒸气于10℃、85kPa下凝结为液体水过 程的Q、W、 H 及U 。已知100℃、101.325kPa下 水的vapHm=40.63kJ· -１ mol
H 2 O( g ) 100C 101.325kPa H 2 O( g ) 25C 3.167kPa
可逆相变条件：
dp=0, dT=0 , p =f(T)
可逆相变的判断：
熔点、沸点、凝固点 液体在某温度下的饱和蒸气压 固体在某温度下的饱和蒸气压
10
(2)不可逆相变：指定温度，非平衡压力下所发生的相变叫 不可逆相变。 或者相变前后温度、压力改变。 例：
11
3. 相变焓（可逆相变焓）
(1)定义: 1mol纯物质发生可逆相变时与环境交换的热叫摩尔相变热， 也称为摩尔相变焓.
B
B
H m
根据可逆相变条件: dp=0,dT=0
Q Q p H n H m
12
(2)相变的标记法及摩尔相变焓之间的相互关系:
1
T2 p2 p T1 1

1
1

4
p1V1 p2V2

5. 绝热可逆过程体积功的计算
方法一：
V2 p V nRT dV 0 0 dV W r pd V V1 V V1 V V2 1 p0V0 p0V0 dV ( V21 V11 ) V1 V 1
忽略压力对相变焓的影响
17
例7：已知下列热力学数据：
100℃水的摩尔蒸发焓为40.63kJ· -1 , mol
C p ,m (H 2O, l) 5.59J mol 1K 1
C p ,m (H 2O, g) 33.795J mol 1 K 1
试求：水在25℃的摩尔蒸发焓。
H 3 nC p,m ( g )dT 2535.0J
T2
T1
H H 1 H 2 H 3 43.73 103 J
1 vap H m ( 25C ) H 43.76 103 J mol 1 n
20
5. 不可逆相变过程热的求解——设计过程
H 2 O( s ) H 2O(l() ) H 2O l 5 C 25CC 5 101.325kPa 101.325kPa 101.325kPa
H 22O(s))O(g ) H OH 2 (g 255110C C C 101..101kPa kPa 101325kPa 325.325
n H2O (s) T1 =253.15K H3
H2
n H2O ( s ) T2=273.15K
m n 55.56mol M
H1 nC p,m ( l )dT 83.687kJ
T1
T2
H 2 ns H m (0C ) n( ls H m ) 333.327kJ l
n H2O ( l ) T1 =253.15K H n H2O (s) T1 =253.15K
21
解：p=101.325kPa
n H2 O ( l ) T1 =253.15K
T2
1
H
n H2O (s) T1 =253.15K H3 nC p,m ( s )dT T
T1
2
H1 T nC p,m( l )dT n H2 O ( l ) T2 = 273.15 K H2
H 2O(l) T1 298.15K p1 3.167kPa
n vap H m ( 25 C )

H
H 2O(g) T1 298.15K p1 3.167kPa
18
试求：25℃ 水的摩尔蒸发焓。
H 2O(l) T1 298.15K p1 3.167kPa
T2
1
H 2O(l),2mol
p2 101.325kPa
H1 nC p,m ( g )dT .... J
T1
ΔU ΔH Δ pV ΔH pV g
H 2 n H m n( vap H m ) ... J
例：B物质，在T1，p1时有vapHm(T1)
在T2，p2时有vapHm(T2)
vapHm(T1) ~ vapHm(T2)的关系？
14
设计过程：
B(l), 1mol T2 , p2
Hm(l)
vapHm(T2)
B(g), 1mol T2 , p2
Hm(g)
B(l), 1mol T1 , p1
n H2O ( s ) T2 = 273.15 K ns H m ( 0C ) n( ls H m ) l
H H1 H 2 H 3
22
p=101.325kPa
n H2 O ( l ) T1 =253.15K
H1 n H2O ( l ) T2=273.15K
H
V2
方法二:
由绝热可逆过程方程求出终态温度T2，再求体积功.
ΔU n CV ,mdT n CV ,m (T2 T1 )
T1
T2
U Q W
Wr ΔU
Q0
5
常见pg单纯pVT变化过程： Q
恒容过程(dV= 0) 恒压过程(dp= 0) 恒温可逆过程 (dT= 0,可逆) 恒温不可逆过程 (dT= 0) 绝热可逆过程 ( Qr = 0) 绝热不可逆过程 ( Q = 0) 自由膨胀过程 (p环=0) 恒温自由膨胀过程 (p环=0)
平衡相变＋pVT 变化 例8： 求压力 101.325 kPa 下，1 kg - 20 ℃的过冷水 凝固为同温同压的冰的过程的Q、W、ΔU、ΔH。
已知水的正常凝固点为 0 ℃ ， 在此条件下冰的熔化焓为 5999.4 J · -1 ， mol 过冷水的定压摩尔热容为 75.312 J · -1 · -1 mol K 冰的定压摩尔热容为 37.604 J · -1 · -1 。 mol K
Bs
Bl
ls H m fus H m s H m l
Bs
B g
gs H m sub H m sg H m
Bl
B g
gl H m vap H m lg H m
13
4. 相变焓与温度的关系
相变 H m f (T )
H 3 nC p,m ( s )dT 41.786kJ
T2 T1
H 291.43kJ
23
p=101.325kPa Q、W、ΔU、ΔH
n H2O ( l ) T1 =253.15K H1 n H2O ( l ) T2=273.15K
H
n H2O (s) T1 =253.15K H3
vapHm(T1)
B(g), 1mol T1 , p1