热力学第二定律可逆与不可逆过程

热力学第二定律（英文：second law of thermodynamics）是热力学的四条基本定律之一，表述热力学过程的不可逆性——孤立系统自发地朝着热力学平衡方向──最大熵状态──演化，同样地，第二类永动机永不可能实现。

这一定律的历史可追溯至尼古拉·卡诺对于热机效率的研究，及其于1824年提出的卡诺定理。

定律有许多种表述，其中最具代表性的是克劳修斯表述（1850年）和开尔文表述（1851年），这些表述都可被证明是等价的。

定律的数学表述主要借助鲁道夫·克劳修斯所引入的熵的概念，具体表述为克劳修斯定理。

虽然这一定律在热力学范畴内是一条经验定律，无法得到解释，但随着统计力学的发展，这一定律得到了解释。

这一定律本身及所引入的熵的概念对于物理学及其他科学领域有深远意义。

定律本身可作为过程不可逆性[2]:p.262及时间流向的判据。

而路德维希·玻尔兹曼对于熵的微观解释——系统微观粒子无序程度的量度，更使这概念被引用到物理学之外诸多领域，如信息论及生态学等克劳修斯表述克劳修斯克劳修斯表述是以热量传递的不可逆性（即热量总是自发地从高温热源流向低温热源）作为出发点。

虽然可以借助制冷机使热量从低温热源流向高温热源，但这过程是借助外界对制冷机做功实现的，即这过程除了有热量的传递，还有功转化为热的其他影响。

1850年克劳修斯将这一规律总结为：不可能把热量从低温物体传递到高温物体而不产生其他影响。

开尔文表述参见：永动机#第二类永动机开尔文勋爵开尔文表述是以第二类永动机不可能实现这一规律作为出发点。

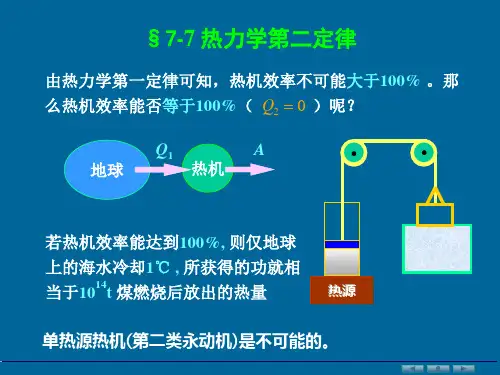
第二类永动机是指可以将从单一热源吸热全部转化为功，但大量事实证明这个过程是不可能实现的。

功能够自发地、无条件地全部转化为热；但热转化为功是有条件的，而且转化效率有所限制。

也就是说功自发转化为热这一过程只能单向进行而不可逆。

1851年开尔文勋爵把这一普遍规律总结为：不可能从单一热源吸收能量，使之完全变为有用功而不产生其他影响。

热力学第二定律的特点
热力学第二定律的特点包括以下5个方面：
1.方向性：热力学第二定律指出，自然过程的进行是有方向性的，即某些过程可以自
发的发生，而另一些过程则不能。

例如，热量可以从高温物体自发地传递到低温物体，而相反的过程则不能自发地发生。

2.不可逆性：热力学第二定律揭示了时间的箭头，即时间是单向流逝的，自然过程具
有不可逆性。

例如，一个气体分子的熵会随着时间的推移而增加，而减少熵的过程则是不可能发生的。

3.普遍性：热力学第二定律是一个普适的定律，适用于所有物质和所有物理过程。

无
论是固体、液体还是气体，无论是化学反应还是物理过程，都受到热力学第二定律的制约。

4.统计性：热力学第二定律是基于统计规律得出的，它描述的是大量粒子或分子的集
体行为。

对于单个分子或少量分子的行为，热力学第二定律并不适用。

5.热力学概率：热力学第二定律指出，一个孤立系统的熵总是倾向于增加，这反映了
系统无序度的增加。

同时，系统的有序度的增加也是可能的，但需要外部的干预，例如能量的输入。

因此，热力学第二定律也反映了自然过程的“涨落”和“概率性”。

总之，热力学第二定律是物理学中的基本定律之一，它描述了自然过程的进行方式和方向，揭示了时间的箭头和不可逆性，同时也反映了物质和能量的统计性质和概率性质。

热力学第二定律熵与不可逆过程的关系热力学是研究物质能量转化和转移规律的科学分支。

该学科中的第二定律是描述系统热力学性质的重要原理。

而熵则是热力学中一个重要的概念，用于衡量系统的无序程度。

本文将探讨热力学第二定律与熵以及不可逆过程之间的关系。

第一节热力学第二定律的基本原理热力学第二定律，也被称为熵增原理，它给出了一个能量转化的方向性，规定自然界中热能只能从高温向低温的方向传递。

具体来说，第二定律可能有多个表述方式，其中最常见的是开尔文表述和克劳修斯表述。

第二节熵的概念及其表达方式熵是热力学中的一个重要概念，用来描述系统的无序程度。

熵的增加可以看作是对系统破坏性的度量，是一个可观测的物理量。

熵的计算有多种表达方式，最常用的是基于微观状态数的玻尔兹曼熵公式。

第三节热力学第二定律与熵的关系热力学第二定律与熵有着密切的关系。

熵的增加可以看作是自然界朝着更加无序状态的一种趋势。

根据热力学第二定律的熵增原理，任何一个孤立系统的熵都不会减少。

因此，可以将熵视为热力学第二定律的一种量化表示。

第四节不可逆过程与熵增不可逆过程是热力学中的一个重要概念，它是指系统经历的过程中不能恢复为初始状态的过程。

而在不可逆过程中，系统的熵会增加。

这表明熵是衡量不可逆性的一个重要指标。

不可逆过程的例子包括热传导、摩擦、扩散等等。

第五节熵增定理及其应用熵增定理是研究熵与不可逆过程关系的重要定理。

它指出，在任何不可逆过程中，系统与周围环境的总熵只能增加，而不能减少。

通过熵增定理，我们可以判断一个过程是否可逆，以及预测系统的演化方向。

总结本文探讨了热力学第二定律、熵和不可逆过程之间的关系。

熵作为一种度量系统无序程度的物理量，与热力学第二定律密切相关。

熵增原理和熵增定理为我们理解系统能量转化和转移规律提供了重要的依据。

通过对熵和不可逆过程的研究，可以更好地应用热力学的知识，预测和优化系统的行为。

热力学第二定律的六种表述热力学第二定律是热力学中最基本的定律之一，它描述了热量的自然流动方向和热量转化的效率。

下面将从六种不同的表述角度来探讨热力学第二定律的含义和应用。

1. 热量不会自发地从低温物体传递到高温物体。

这是热力学第二定律最常见的表述方式。

它告诉我们，热量的自然流动方向是从高温物体向低温物体，而不会反过来。

这也是为什么我们需要加热器来加热房间，而不是用冷却器来冷却房间的原因。

2. 热量不可能完全转化为功。

这个表述方式告诉我们，热量和功之间存在一定的转化效率。

即使我们使用最高效的热机，也无法将所有的热量转化为功。

这是因为热量的自然流动方向是从高温物体向低温物体，而功需要从低温物体向高温物体传递。

3. 熵的增加是不可避免的。

熵是一个描述系统无序程度的物理量。

热力学第二定律告诉我们，任何封闭系统的熵都会不可避免地增加。

这意味着系统的有序程度会不断降低，最终趋向于混沌状态。

这也是为什么我们需要不断输入能量来维持系统的有序状态。

4. 热力学第二定律是不可逆的。

这个表述方式告诉我们，热力学第二定律是一个不可逆的过程。

一旦热量从高温物体向低温物体流动，就无法逆转这个过程。

这也是为什么我们需要不断输入能量来维持系统的有序状态。

5. 热力学第二定律是宇宙中最普遍的定律。

这个表述方式告诉我们，热力学第二定律是宇宙中最普遍的定律之一。

无论是在地球上还是在宇宙中的其他星球上，热力学第二定律都适用。

这也是为什么我们需要不断输入能量来维持系统的有序状态。

6. 热力学第二定律是能量守恒定律的补充。

这个表述方式告诉我们，热力学第二定律是能量守恒定律的补充。

虽然能量守恒定律告诉我们能量不能被创造或销毁，但它并没有告诉我们能量的自然流动方向和转化效率。

热力学第二定律则提供了这些信息，使我们能够更好地理解能量的本质和转化过程。

热力学第二定律是热力学中最基本的定律之一，它描述了热量的自然流动方向和热量转化的效率。

通过不同的表述方式，我们可以更好地理解这个定律的含义和应用。

热力学第二定律的推导过程热力学是研究物质内部能量转化和传递规律的学科，而热力学第二定律则是研究能量转化方向的规律。

本文将探讨热力学第二定律的推导过程。

1. 序言热力学第二定律是热力学最重要的基本定律之一，它描述了自然界中热能传递的不可逆性。

通过推导热力学第二定律，我们可以更好地理解能量转化的规律。

2. 卡诺循环为了推导热力学第二定律，我们首先介绍卡诺循环。

卡诺循环是一种理想的循环过程，它由两个等温过程和两个绝热过程组成。

在卡诺循环中，热量从高温热源吸收，经过绝热膨胀，再通过等温压缩过程排放至低温热源。

3. 卡诺效率我们知道，能量守恒是一个自然界的基本原则。

在理想的卡诺循环中，系统对外做功等于从高温热源吸收的热量减去排放给低温热源的热量。

设高温热源的温度为Th，低温热源的温度为Tl，根据热力学基本方程，我们可以推导出卡诺循环的效率：η = 1 - (Tl/Th)其中，η表示卡诺循环的效率。

4. 温度与熵的关系接下来，我们引入熵的概念。

熵是一个衡量系统有序程度的物理量。

设一个系统的熵变为dS，热量的传递为dQ，温度为T。

根据热力学基本方程，我们可以得到：dS = dQ/T这个方程表明，当系统吸收热量时，熵会增加；当系统排放热量时，熵会减少。

5. 热力学第二定律有了温度与熵的关系，我们可以推导出热力学第二定律。

根据热力学第一定律，能量守恒是永恒不变的。

然而，通过观察自然界中热能传递现象，我们发现自然界中热量从高温物体向低温物体传递，而不会反过来。

根据温度与熵的关系，当两个系统接触并达到热平衡时，它们的熵变应为零：dS = dQ1/T1 + dQ2/T2 = 0上式表明，当热量从高温物体传递到低温物体时，总是满足T1/T2 > 1。

这就是热力学第二定律的表达式。

6. 推广热力学第二定律的推广形式是开尔文-普朗克表述形式。

根据开尔文-普朗克表述，任何一个不可逆过程都可以看作是一个可逆过程与一个热库接触的情况。