2020年高考物理4.14 竖直面内或斜面内的圆周运动的绳模型(提高篇)(含解析)

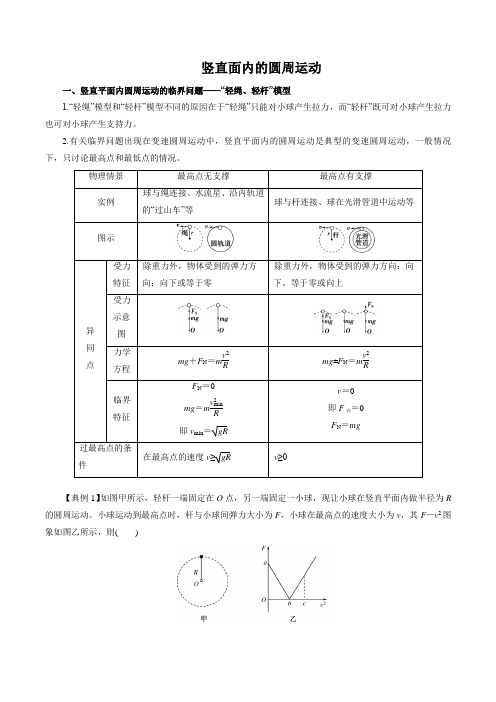
竖直面内的圆周运动一、竖直平面内圆周运动的临界问题——“轻绳、轻杆”模型1.“轻绳”模型和“轻杆”模型不同的原因在于“轻绳”只能对小球产生拉力，而“轻杆”既可对小球产生拉力也可对小球产生支持力。

2.有关临界问题出现在变速圆周运动中，竖直平面内的圆周运动是典型的变速圆周运动，一般情况下，只讨论最高点和最低点的情况。

物理情景最高点无支撑最高点有支撑实例球与绳连接、水流星、沿内轨道的“过山车”等球与杆连接、球在光滑管道中运动等图示异同点受力特征除重力外，物体受到的弹力方向：向下或等于零除重力外，物体受到的弹力方向：向下、等于零或向上受力示意图力学方程mg＋F N＝mv2R mg±F N＝mv2R临界特征F N＝0mg＝mv2minR即v min＝gRv＝0即F向＝0F N＝mg过最高点的条件在最高点的速度v≥gR v≥0【典例1】如图甲所示，轻杆一端固定在O点，另一端固定一小球，现让小球在竖直平面内做半径为R 的圆周运动。

小球运动到最高点时，杆与小球间弹力大小为F，小球在最高点的速度大小为v，其F－v2图象如图乙所示，则()A ．小球的质量为aRbB ．当地的重力加速度大小为RbC ．v 2＝c 时，小球对杆的弹力方向向上D ．v 2＝2b 时，小球受到的弹力与重力大小相等 【答案】： ACD【典例2】用长L ＝ 0.6 m 的绳系着装有m ＝ 0.5 kg 水的小桶，在竖直平面内做圆周运动，成为“水流星”。

G ＝10 m/s 2。

求：(1) 最高点水不流出的最小速度为多少？(2) 若过最高点时速度为3 m/s ，此时水对桶底的压力多大？ 【答案】 (1) 2.45 m/s (2) 2.5 N 方向竖直向上【解析】(1) 水做圆周运动，在最高点水不流出的条件是：水的重力不大于水所需要的向心力。

这是最小速度即是过最高点的临界速度v 0。

以水为研究对象， mg ＝m v 20L解得v 0＝Lg ＝0.6×10 m/s ≈ 2.45 m/s(2) 因为 v ＝ 3 m/s>v 0，故重力不足以提供向心力，要由桶底对水向下的压力补充，此时所需向心力由以上两力的合力提供。

2020年高考物理最新考点模拟试题：竖直面内或斜面内的圆周运动的绳模型（提高篇）（解析版）一．选择题1．（2019沈阳三模）如图所示，水平地面上有一光滑弧形轨道与半径为r的光滑圆轨道相连，且固定在同一个竖直面内。

将一只质量为m的小球由圆弧轨道上某一高度处无初速释放。

为使小球在沿圆轨道运动时始终不脱离轨道，这个高度h的取值可为（）A．2.2r B．1.2r C．1.6r D．0.8r【参考答案】D【命题意图】本题考查机械能守恒定律、牛顿运动定律及其相关知识点。

【解题思路】为使小球在沿圆轨道运动时始终不脱离轨道，一种是小球沿圆轨道运动到不超过与圆心等高的位置；一种是能够通过光滑圆轨道的最高点。

若小球沿圆轨道运动到不超过与圆心等高的位置，设其无初速释放小球的最大高度为h1，由机械能守恒定律，mgh1=mgr，解得h1=r，即高度h的取值不大于r。

若小球能够通过光滑圆轨道的最高点，设恰能通过光滑圆轨道的最高点时的速度为v，在最高点，由牛顿第二定律，mg=m2vr，设小球能够通过光滑圆轨道的最高点，无初速释放小球的最小高度为h2，由机械能守恒定律，mgh2=2mgr+12mv2，解得h2=2.5r，即高度h的取值必须不小于2.5r。

综合上述分析可知选项D正确。

2．如图所示，一质量为M的人站在台秤上，一根长为R的悬线一端系一个质量为m的小球，手拿悬线另一端，小球绕悬线另一端点在竖直平面内做圆周运动，且小球恰好能通过圆轨道最高点，则下列说法正确的是( )A．小球运动到最高点时，小球的速度为零B．当小球运动到最高点时，台秤的示数最小，且为MgC．小球在a、b、c三个位置时，台秤的示数相同D．小球从最高点运动到最低点的过程中台秤的示数增大，人处于超重状态【参考答案】 C【名师解析】小球恰好能通过圆轨道最高点，由mg＝m v2R，得v＝gR，A项错误；当小球恰通过圆轨道最高点b时，悬线拉力为0，此时对人受力分析，得出台秤对人的支持力F＝Mg，在a、c两处时小球受重力和水平指向圆心的拉力，台秤对人的支持力也为F＝Mg，即台秤的示数也为Mg，故C项正确；小球在a、c连线以上(不包括b点)时，人受到悬线斜向上的拉力，人对台秤的压力小于Mg，在a、c连线以下时，人受到悬线斜向下的拉力，人对台秤的压力大于Mg，人处于平衡态，没有超、失重现象，B、D两项错误。

三大力场中竖直面内圆周运动模型特训目标特训内容目标1重力场中的竖直面内圆周运动的绳(或轨道内侧)模型(1T -6T )目标2重力场中的竖直面内圆周运动的杆(或管)模型(7T -12T )目标3电磁场中的竖直面内圆周运动模型(13T -18T )【特训典例】一、重力场中的竖直面内圆周运动的绳(或轨道内侧)模型1如图a ，在竖直平面内固定一光滑的半圆形轨道ABC ，小球以一定的初速度从最低点A 冲上轨道，图b 是小球在半圆形轨道上从A 运动到C 的过程中，其速度平方与其对应高度的关系图像。

已知小球在最高点C 受到轨道的作用力为2.5N ，空气阻力不计，B 点为AC 轨道中点，重力加速度g 取10m/s 2，下列说法正确的是()A.图b 中x =25m 2/s 2B.小球质量为0.2kgC.小球在A 点时重力的功率为5WD.小球在B 点受到轨道作用力为8.5N【答案】ABD【详解】A ．小球在光滑轨道上运动，只有重力做功，故机械能守恒，有12mv 2A =12mv 2h +mgh 解得v 2A =v 2h +2gh 即x =9+2×10×0.8 m 2/s 2=25m 2/s 2，A 正确；B ．依题意小球在C 点，有F +mg =m v 2C R 又v 2C =9m 2/s 2，2R =0.8m 解得m =0.2kg ，B 正确；C ．小球在A 点时重力方向竖直向下，速度水平向右，二者夹角为90°，根据P =mgv cos θ可知重力的瞬时功率为零，C 错误；D ．由机械能守恒，可得12mv 2A =12mv 2B +mgR 又因为小球在B 点受到的在水平方向上的合外力提供向心力，可得F B =mv 2BR联立，可得F B =8.5N ，D 正确。

故选ABD 。

2如图甲所示，一长为R 的轻绳，一端系在过O 点的水平转轴上，另一端固定一质量未知的小球，整个装置绕O 点在竖直面内转动，小球通过最高点时，绳对小球的拉力F 与其速度平方v 2的关系图像如图乙所示，图线与纵轴的交点坐标为a ，下列判断正确的是()A.利用该装置可以得出重力加速度，且g =RaB.绳长不变，用质量较大的球做实验，得到的图线斜率更大C.绳长不变，用质量较小的球做实验，得到的图线斜率更大D.绳长不变，用质量较小的球做实验，图线与纵轴的交点坐标不变【答案】CD【详解】A ．由图乙知当F =0时，v 2=a ，则有mg =mv 2R =ma R 解得g =a R 故A 错误；BC ．在最高点，根据牛顿第二定律得F +mg =m v 2R整理得v 2=R m F +gR 图线的斜率为k =Rm 可知绳长不变，小球的质量越小，斜率越大，故B 错误，C 正确；D ．由表达式v 2=RmF +gR 可知，当F =0时，有v 2=gR =a 可知图线与纵轴的交点坐标与小球质量无关，故D 正确。

专题4.14 竖直面内或斜面内的圆周运动的杆模型一．选择题1. （2018北京密云质检）如图所示甲、乙、丙、丁是游乐场中比较常见的过山车，甲、乙两图的轨道车在轨道的外侧做圆周运动，丙、丁两图的轨道车在轨道的内侧做圆周运动，两种过山车都有安全锁(由上、下、侧三个轮子组成)把轨道车套在了轨道上，四个图中轨道的半径都为R ，下列说法正确的是( )A ．甲图中，当轨道车以一定的速度通过轨道最高点时，座椅一定给人向上的力B ．乙图中，当轨道车以一定的速度通过轨道最低点时，安全带一定给人向上的力C ．丙图中，当轨道车以一定的速度通过轨道最低点时，座椅一定给人向上的力D ．丁图中，轨道车过最高点的最小速度为gR 【参考答案】.BC【名师解析】甲图中，由mg=m 2v R 可知，当轨道车以一定的速度v=gR 通过轨道最高点时，座椅给人向上的力为零，选项A 错误；乙图中，由F -mg=m 2v R 可知，当轨道车以一定的速度通过轨道最低点时，安全带一定给人向上的力F = mg+m 2v R ，选项B 正确；丙图中，由F -mg=m 2v R可知，当轨道车以一定的速度通过轨道最低点时，座椅一定给人向上的力F = mg+m 2v R，选项C 正确；由于过山车都有安全锁(由上、下、侧三个轮子组成)把轨道车套在了轨道上，丁图中，轨道车过最高点的最小速度可以为零，选项D 错误。

2. (2017·辽宁铁岭联考)飞机由俯冲到拉起时，飞行员处于超重状态，此时座椅对飞行员的支持力大于飞行员所受的重力，这种现象叫过荷。

过荷过重会造成飞行员四肢沉重，大脑缺血，暂时失明，甚至昏厥。

受过专门训练的空军飞行员最多可承受9倍重力的影响。

g取10 m/s2，则当飞机在竖直平面上沿圆弧轨道俯冲、拉起的速度为100 m/s时，圆弧轨道的最小半径为( )图10A.100 mB.111 mC.125 mD.250 m【参考答案】C3.(2017·山东青岛期末) (多选)如图11所示，内壁光滑的大圆管，用一细轻杆固定在竖直平面内；在管内有一小球(可视为质点)做圆周运动。

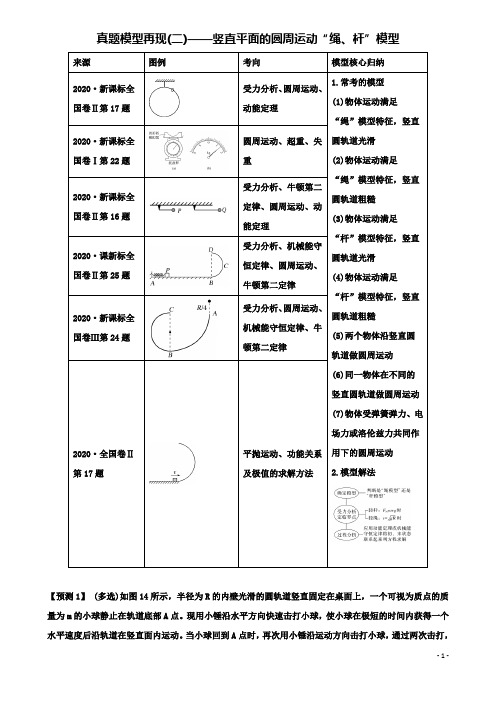
真题模型再现(二)——竖直平面的圆周运动“绳、杆”模型来源图例考向模型核心归纳2020·新课标全国卷Ⅱ第17题受力分析、圆周运动、动能定理1.常考的模型(1)物体运动满足“绳”模型特征，竖直圆轨道光滑(2)物体运动满足“绳”模型特征，竖直圆轨道粗糙(3)物体运动满足“杆”模型特征，竖直圆轨道光滑(4)物体运动满足“杆”模型特征，竖直圆轨道粗糙(5)两个物体沿竖直圆轨道做圆周运动(6)同一物体在不同的竖直圆轨道做圆周运动(7)物体受弹簧弹力、电场力或洛伦兹力共同作用下的圆周运动2.模型解法2020·新课标全国卷Ⅰ第22题圆周运动、超重、失重2020·新课标全国卷Ⅱ第16题受力分析、牛顿第二定律、圆周运动、动能定理2020·课新标全国卷Ⅱ第25题受力分析、机械能守恒定律、圆周运动、牛顿第二定律2020·新课标全国卷Ⅲ第24题受力分析、圆周运动、机械能守恒定律、牛顿第二定律2020·全国卷Ⅱ第17题平抛运动、功能关系及极值的求解方法【预测1】 (多选)如图14所示，半径为R的内壁光滑的圆轨道竖直固定在桌面上，一个可视为质点的质量为m的小球静止在轨道底部A点。

现用小锤沿水平方向快速击打小球，使小球在极短的时间内获得一个水平速度后沿轨道在竖直面内运动。

当小球回到A点时，再次用小锤沿运动方向击打小球，通过两次击打，小球才能运动到圆轨道的最高点。

已知小球在运动过程中始终未脱离轨道，在第一次击打过程中小锤对小球做功W 1，第二次击打过程中小锤对小球做功W 2。

设先后两次击打过程中小锤对小球做功全部用来增加小球的动能，则W 1W 2的值可能是( )图14 A.34 B.13 C.23D.1解析 第一次击打后球最多到达与球心O 等高位置，根据功能关系，有W 1≤mgR，两次击打后球可以运动到轨道最高点，根据功能关系，有W 1＋W 2－2mgR ＝12mv 2，在最高点有mg ＋N ＝m v2R ≥mg，由以上各式可解得W 1≤mgR，W 2≥32mgR ，因此W 1W 2≤23，B 、C 正确。

甲 乙如图乙所示，汽车经过凹形桥面最低点时，受竖直向下的重力和竖直向上的支持力，两个力的合力提m v 2r ，故F N ＝G ＋m v 2r 。

由牛顿第三定律得：汽车对凹形桥面的压力二．竖直面内圆周运动的轻绳(过山车)模型小球沿竖直光滑轨道内侧做圆周运动，小球在细绳作用下在竖直平面内做圆周运动，都是绳模型，如甲 乙小球运动到最高点时受向下的重力和向下的绳子拉力(或轨道弹力)作用，由这两个力的合力提供向心三．竖直面内圆周运动的轻杆(管)模型小球被一轻杆拉着在竖直平面内做圆周运动，小球在竖直放置的光滑细管内做圆周运动，都是杆模型，甲 乙【答案】（1）2m/s；（2）15N'2v【答案】（1）汽车过凹形桥面最低点时，汽车对桥面的压力较大；【详解】（1）汽车以相同速率分别通过凹形桥面最低点和凸形桥面最高点时，受力分析如图通过凹形桥面最低点由牛顿第二定律可知1N mg -解得1N mg =通过凸形桥面最高点由牛顿第二定律可知A.数据a与小球的质量有关B.数据b与小球的质量无关C.比值ba只与小球的质量有关，与圆周轨道半径无关D.利用数据a、b和g能够求出小球的质量和圆周轨道半径A.当地的重力加速度大小为R bB.小球的质量为a b RA．500N B 【答案】C【详解】根据牛顿第二定律解得A．小球通过管道最低点时，管道对地面的压力为B．小球通过管道最高点时，管道对地面的压力可能大于C．小球通过管道最高点时，管道对地面的压力不可能为零DA．小球在轨道最低点的机械能最大B．小球在轨道最低点对轨道的压力最大A．在A→B过程中，速度增大A．3mg【答案】D【详解】在最高点，根据牛顿第二定律可得A．小球不能到达PB．小球到达P点时轻杆受到的弹力为C．小球能到达P点，且在D．小球能到达P点，且在【答案】C【详解】A．根据机械能守恒A ．1N mg <B ．1N mg =C ．A ．10m/s B ．20m/s 【答案】B【详解】要使汽车行驶至桥顶时对桥顶恰无压力，则有A ．若0v gR =，则物体对半球顶点压力为B ．若012v gR =，则物体对半球顶点的压力为0v =A．3:2B．2:3C．2:1【答案】B【详解】在最高点，根据牛顿第二定律A．36km/h B C．70km/h DA．若速度大小为B．若速度大小为C．若速度大小为D．若速度大小为A．当地的重力加速度大小为R bC．v2=c时，杆对小球弹力方向向下【答案】BCA．小球的质量为2kgB．固定圆环的半径R为0.4mC．小球在最高点速度为4m/s时，圆环受到小球施加的竖直向下D．若小球恰好能做完整圆周运动，则其运动中所受圆环给的最大弹力为【答案】（1）2gL；（【详解】（1）球B在最高点时只受重力作用，根据牛顿第二定律有得【答案】（1）22m/s；（2【详解】（1）小球要做完整圆周运动，在最高点当重力提供向心力时，速度最小，则有r=，解得其中0.8m【答案】（1）10m；（2）24N【详解】（1）木块经B点时，对轨道的压力恰好为零，重力刚好提供向心力，则有解得轨道半径的大小为【答案】（1）2 m/s；（2）【详解】（1）在最高点，由牛顿第二定律得由于轻绳对小球只能提供指向圆心的拉力，即【答案】（1）【详解】（1）要使小球在竖直面内能够做完整的圆周运动，在最高点时重力恰好提供向心力，则有解得在竖直方向有在水平方向有由几何关系得【答案】若F向上，【详解】杆在最高点处，球的重力与杆的弹力的合力提供球的向心力。

高考物理100考点最新模拟题千题精练第四部分 曲线运动专题4.16．竖直面内或斜面内的圆周运动的绳模型（基础篇）一．选择题1.（2020年4月浙江台州质量评估）跳绳过程中，甲、乙两位同学握住绳子两端 A 、B 近似不动，绳子绕 AB 连线在空中转到图示位置时，则质点A ．P 、Q 的速度方向沿绳子切线B ．P 的线速度小于 Q 的线速度C ．P 的角速度小于 Q 的角速度D ．P 、Q 的合外力方向指向 AB 的中点 O【参考答案】B 【命题意图】 本题以跳绳为情景，考查圆周运动、曲线运动的速度方向、加速度方向和公式v=ωr 的理解及其相关知识点，考查的核心素养是“运动和力”的观点。

【解题思路】根据题述，绳子绕 AB 连线在空中转到图示位置时，其AB 为转轴，绳子上各质点都是以AB 为轴在垂直AB 的平面内转动，P 、Q 的速度方向沿转动圆轨迹的切线方向，不是沿绳子切线方向，选项A 错误；绳子绕 AB 连线在空中做圆周运动时，各个质点的角速度相同，即P 的角速度等于 Q 的角速度，选项C 错误；由图可知，P 的轨迹半径小于Q 的轨迹半径，由线速度与角速度和半径的关系式，v=ωr ，可知P 的线速度小于 Q 的线速度，选项B 正确；P 、Q 的合外力方向指向各自圆轨迹的圆心，选项D 错误。

2..如图所示，一倾斜的圆筒绕固定轴OO 1以恒定的角度ω转动，圆筒的半径r ＝1.5 m ．筒壁内有一小物体与圆筒始终保持相对静止，小物体与圆筒间的动摩擦因数为32(设最大静摩擦力等于滑动摩擦力)，转动轴与水平面间的夹角为60°，重力加速度g 取10 m/s 2.则ω的最小值是( )A O甲乙A．1 rad/s B.303rad/sC.10 rad/s D．5 rad/s【参考答案】C【名师解析】由于小物体在圆筒内随圆筒做圆周运动，其向心力由小物体受到的指向圆心(转动轴)的合力提供．在小物体转到最上面时最容易与圆筒脱离，根据牛顿第二定律，沿半径方向F N＋mg cos 60°＝mω2r，又沿筒壁方向mg sin 60°≤μF N，解得ω≥10 rad/s，要使小物体与圆筒始终保持相对静止，则ω的最小值是10 rad/s，选项C正确．3.（4分）（2019山东济南期末）如图所示，固定在水平地面上的圆弧形容器，容器两端A、C在同一高度上，B为容器的最低点，圆弧上E、F两点也处在同一高度，容器的AB段粗糙，BC段光滑。

2020年高考物理专题精准突破专题竖直面内的圆周运动【专题诠释】均是没有支撑的小球均是有支撑的小球【高考领航】【2019·江苏卷】如图所示，摩天轮悬挂的座舱在竖直平面内做匀速圆周运动．座舱的质量为m，运动半径为R，角速度大小为ω，重力加速度为g，则座舱（）A．运动周期为2πRB．线速度的大小为ωRC．受摩天轮作用力的大小始终为mg D．所受合力的大小始终为mω2R【答案】BD【解析】由于座舱做匀速圆周运动，由公式2πTω=，解得：2πT ω=，故A 错误；由圆周运动的线速度与角速度的关系可知，v R ω=，故B 正确；由于座舱做匀速圆周运动，所以座舱受到摩天轮的作用力是变力，不可能始终为mg ，故C 错误；由匀速圆周运动的合力提供向心力可得：2F m R ω=合，故D 正确。

【2018·天津卷】滑雪运动深受人民群众的喜爱，某滑雪运动员（可视为质点）由坡道进入竖直面内的圆弧 形滑道AB ，从滑道的A 点滑行到最低点B 的过程中，由于摩擦力的存在，运动员的速率不变，则运动员沿 AB 下滑过程中（ ）A ．所受合外力始终为零B ．所受摩擦力大小不变C ．合外力做功一定为零D ．机械能始终保持不变 【答案】C【解析】根据曲线运动的特点分析物体受力情况，根据牛顿第二定律求解出运动员与曲面间的正压力变化情况，从而分析运动员所受摩擦力变化；根据运动员的动能变化情况，结合动能定理分析合外力做功；根据运动过程中，是否只有重力做功来判断运动员的机械能是否守恒；因为运动员做曲线运动，所以合力一定不为零，A 错误；运动员受力如图所示，重力垂直曲面的分力与曲面对运动员的支持力的合力充当向心力，故有22cos cos N N v v F mg m F m mg R Rθθ-=⇒=+，运动过程中速率恒定，且θ在减小，所以曲面对运动员的支持力越来越大，根据N f F μ=可知摩擦力越来越大，B 错误；运动员运动过程中速率不变，质量不变，即动能不变，动能变化量为零，根据动能定理可知合力做功为零，C 正确；因为克服摩擦力做功，机械能不守恒，D 错误。

专题4.14竖直面内或斜面内的圆周运动的绳模型（提高篇）一．选择题1．（2019沈阳三模）如图所示，水平地面上有一光滑弧形轨道与半径为r的光滑圆轨道相连，且固定在同一个竖直面内。

将一只质量为m的小球由圆弧轨道上某一高度处无初速释放。

为使小球在沿圆轨道运动时始终不脱离轨道，这个高度h的取值可为（）A．2.2r B．1.2r C．1.6r D．0.8r【参考答案】D【命题意图】本题考查机械能守恒定律、牛顿运动定律及其相关知识点。

【解题思路】为使小球在沿圆轨道运动时始终不脱离轨道，一种是小球沿圆轨道运动到不超过与圆心等高的位置；一种是能够通过光滑圆轨道的最高点。

若小球沿圆轨道运动到不超过与圆心等高的位置，设其无初速释放小球的最大高度为h1，由机械能守恒定律，mgh1=mgr，解得h1=r，即高度h的取值不大于r。

若小球能够通过光滑圆轨道的最高点，设恰能通过光滑圆轨道的最高点时的速度为v，在最高点，由牛顿第二定律，mg=m2vr，设小球能够通过光滑圆轨道的最高点，无初速释放小球的最小高度为h2，由机械能守恒定律，mgh2=2mgr+12mv2，解得h2=2.5r，即高度h的取值必须不小于2.5r。

综合上述分析可知选项D正确。

2．如图所示，一质量为M的人站在台秤上，一根长为R的悬线一端系一个质量为m的小球，手拿悬线另一端，小球绕悬线另一端点在竖直平面内做圆周运动，且小球恰好能通过圆轨道最高点，则下列说法正确的是( )A ．小球运动到最高点时，小球的速度为零B ．当小球运动到最高点时，台秤的示数最小，且为MgC ．小球在a 、b 、c 三个位置时，台秤的示数相同D ．小球从最高点运动到最低点的过程中台秤的示数增大，人处于超重状态 【参考答案】 C【名师解析】 小球恰好能通过圆轨道最高点，由mg ＝m v 2R，得v ＝gR ，A 项错误；当小球恰通过圆轨道最高点b 时，悬线拉力为0，此时对人受力分析，得出台秤对人的支持力F ＝Mg ，在a 、c 两处时小球受重力和水平指向圆心的拉力，台秤对人的支持力也为F ＝Mg ，即台秤的示数也为Mg ，故C 项正确；小球在a 、c 连线以上(不包括b 点)时，人受到悬线斜向上的拉力，人对台秤的压力小于Mg ，在a 、c 连线以下时，人受到悬线斜向下的拉力，人对台秤的压力大于Mg ，人处于平衡态，没有超、失重现象，B 、D 两项错误。