当前位置：文档之家 › 运筹学-单纯形法证明

运筹学-单纯形法证明

  • 格式：pdf
  • 大小：1.77 MB
  • 文档页数：27

下载文档原格式

  / 27

合集下载

运筹学单纯形法

运筹学单纯形法

只要取 x5=min{-，8/2，12}=4 就有上式成立。 x5=4时， x4=0，故决定用x5换x4 x1 =4- 1/4 x4 x5 =4-1/2 x4 +2 x3 x2 =2+1/8 x4–1/2 x3 代入得 z=14-3/2 x3 –1/8 x4 ，令x3 ，x4=0得z=14。新基可 行解为 X(3) =(4,2,0,0,4) T –为最优解，新顶点Q2 最优目标值z=14 。
§3.4 最优性检验和判别定理
线性规划解的四种可能： 1、有唯一解； 2、无穷多最优解； 3、无界解； 4、无可行解。 何时达最优解, 何种最优解？
将基本可行解X(0)和X(1)分别代入目标函数得
z z
(0)
= ∑ ci xi0
i =1 m
mቤተ መጻሕፍቲ ባይዱ
(1)
= ∑ ci [ xi0 − θ aij ] + θ ci
§3.3 从初始基可行解转换为另一基可行解
0 0 记初始基可行解为X(0),有 X ( 0 ) = (x10 x 2 L x m 0 L 0
)
Pi xi0 = b 该解满足约束方程, 即 ∑
i =1
m
(1)
非基向量可以用基向量的线性组合表示
Pj = ∑ aij Pj
i =1 m
m
(2) (3)
Pj − ∑ aij Pj = 0
从实际例子中分析单纯形法原理的基本框架为 •第一步：将LP线性规划变标准型，确定一个初始可行解 （顶点）。 •第二步：对初始基可行解最优性判别，若最优，停止；否 则转下一步。 •第三步：从初始基可行解向相邻的基可行解（顶点）转 换，且使目标值有所改善—目标函数值增加，重复第二和 第三步直到找到最优解。

运筹学

运筹学

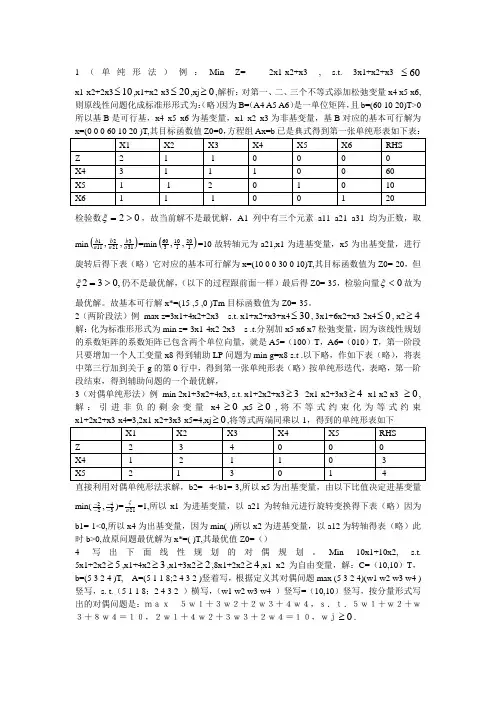
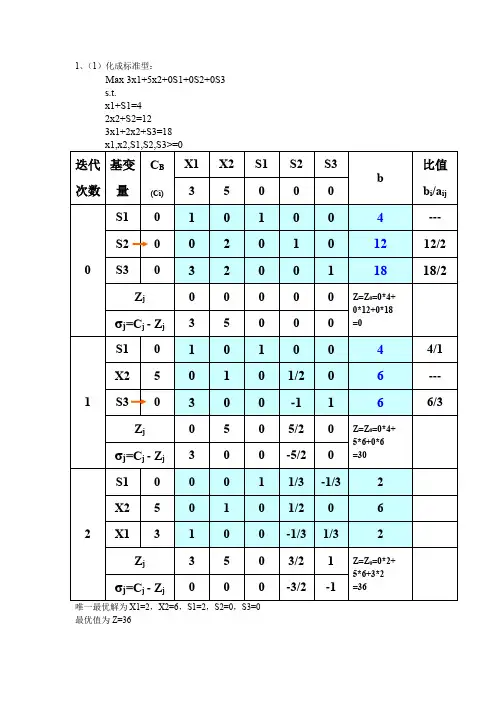
1（单纯形法）例：Min Z=-2x1-x2+x3 , s.t. 3x1+x2+x360≤x1-x2+2x310≤,x1+x2-x320≤,xj 0≥,解析：对第一、二、三个不等式添加松弛变量x4 x5 x6,则原线性问题化成标准形形式为：（略）因为B=（A4 A5 A6）是一单位矩阵，且b=(60 10 20)T>0 所以基B 是可行基，x4 x5 x6为基变量，x1 x2 x3为非基变量，基B 对应的基本可行解为检验数02>=ξ，故当前解不是最优解，A1列中有三个元素a11 a21 a31 均为正数，取min ()313212111,,a b a b a b =min ()120110360,,=10故转轴元为a21,x1为进基变量，x5为出基变量，进行旋转后得下表（略）它对应的基本可行解为x=(10 0 0 30 0 10)T,其目标函数值为Z0=-20，但,032>=ξ仍不是最优解，（以下的过程跟前面一样）最后得Z0=-35，检验向量0<ξ故为最优解。

故基本可行解x*=(15 ,5 ,0 )Tm 目标函数值为Z0=-35。

2（两阶段法）例 max z=3x1+4x2+2x3 s.t. x1+x2+x3+x430≤, 3x1+6x2+x3-2x40≤, x24≥解：化为标准形形式为min z=-3x1-4x2-2x3 s .t.分别加x5 x6 x7松弛变量，因为该线性规划的系数矩阵的系数矩阵已包含两个单位向量，就是A5=（100）T ，A6=（010）T ，第一阶段只要增加一个人工变量x8得到辅助LP 问题为min g=x8 s.t .以下略，作如下表（略），将表中第三行加到关于g 的第0行中，得到第一张单纯形表（略）按单纯形迭代，表略，第一阶段结束，得到辅助问题的一个最优解，3（对偶单纯形法）例 min 2x1+3x2+4x3, s.t. x1+2x2+x33≥ 2x1-x2+3x34≥ x1 x2 x3 0≥,解：引进非负的剩余变量x40≥,x50≥,将不等式约束化为等式约束直接利用对偶单纯形法求解，b2=- 4<b1=-3,所以x5为出基变量，由以下比值决定进基变量min(3422,----)=21a ξ=1,所以x1为进基变量，以a21为转轴元进行旋转变换得下表（略）因为b1=-1<0,所以x4为出基变量，因为min( )所以x2为进基变量，以a12为转轴得表（略）此时b>0,故原问题最优解为x*=( )T,其最优值Z0=（） 4写出下面线性规划的对偶规划。

15单纯形法(运筹学)

15单纯形法(运筹学)
几点说明： 几点说明： (1)、 (1)、例 maxZ=X1 +2X2 X1 ≤ 4 X2 ≤ 3 X1+2X2 ≤ 8 X1 , X2 ≥0 X1+X3 = 4 X2+X4 = 3 X1+2X2+X5= 8 X1 … X5 ≥0
1
2
3
4
X(1)= (2,3) X(2)= (4,2)
全部解： 全部解：X=α
(1) -4 0 1 -2 0
14
15
本问题无界。 本问题无界。 X2
O
X1
Z=0
16
1.5.4 初始基本可行解的求法 (一)、大M法： 一、 法 例1 ： maxZ= 6X1 +4X2 2X1 +3X2 ≤ 100 4X1 +2X2 ≤ 120 X1 X1 X2 ≥0
=14
X2 ≥ 22
17
λj <0
8
(3)、 (3)、maxZ=10X1 + 12X2 3X1+4X2 ≤ 6 4X1+ X2 ≤ 2 3X1 +2X2 ≤ 3 X1 , X2 ≥0
9
10
X =(0, 3/2, 0, 1/2, 0)T Zmax=18
退化解
*
11
例：maxZ= -3/4X4+20X5 -1/2X6+6X7 X1+1/4X4 -8X5 -X6+9X7 =0 X2+1/2X4-12X5 -1/2X6+3X7 =0 X3+X6 =1 X1 … X7 ≥0 (P1 P2 P3) → (P4 P2 P3) → (P1 P2 P3) → (P4 P5 P3) → (P6 P5 P3) → (P6 P7 P3) → (P1 P7 P3)

运筹学-第一章-单纯形法基本原理

运筹学-第一章-单纯形法基本原理
初始基本可行解：
X ( 0) ( x1 , x2 ,, xm ,0,0,...,0)T (b1 , b2 ,......,bm ,0,0,...,0)T
0
0
0
单纯形法基本原理
2、基变换 定义：两个基可行解称为相邻的，如果它们之间变换 且仅变换一个基变量。 初始基可行解的前m个为基变量，
X
凸集
顶点
凸集
不是凸集
顶点：如果凸集C中不存在任何两个不同的点X1，X2，使X 成为这两个点连线上的一个点
单纯形法基本原理
定理1：若线性规划问题存在可行解，则该问题的可行域是 凸集。 定理2：线性规划问题的基可行解X对应可行域(凸集)的顶 点。 定理3：若问题存在最优解，一定存在一个基可行解是最优 解。（或在某个顶点取得）
的左边变成一个单位矩阵，
b (b1 a1 j ,.,bl 1 al 1 j , , bl 1 al 1 j ,.,bm am1 j , ) ( x1 , x2 ,..., xl 1 , x j , xl 1 ,..., xm )
X
(1)
T
与X
( 0)
是相邻的基可行解。
M M bm 0 L
M M
M M
L 1 am,m1 L L 00
M , M amn m
bi 其中： i a kj 0 a kj
j c j ci aij c j z j
单纯形法的计算步骤
例1.12 用单纯形法求下列线性规划的最优解
max Z 3 x1 4 x 2 2 x1 x 2 40 x1 3 x 2 30 x , x 0 1 2
xi0 aij 0, aij 0,取值无限，

运筹学第5章 单纯形法

运筹学第5章 单纯形法

0 0 1
在第一次找可行基时，所找到的基或为单位矩阵或为由单位矩阵的 各列向量所组成，称之为初始可行基，其相应的基本可行解叫初始基 本可行解。如果找不到单位矩阵或由单位矩阵的各列向量组成的基作 为初始可行基，我们将构造初始可行基，具体做法在以后详细讲述。
8Leabharlann §1 单纯形法的基本思路和原理
二、 最优性检验 所谓最优性检验就是判断已求得的基本可行解是否是最优解。
5
§1 单纯形法的基本思路和原理
线性规划解之间的关系：
1.可行解与最优解： 最优解一定是可行解，但可行解不一定是最优解。
2. 可行解与基本解： 基本解不一定是可行解，可行解也不一定是基本解。
3. 可行解与基本可行解： 基本可行解一定是可行解，但可行解不一定是基本可行解。
4. 基本解与基本可行解： 基本可行解一定是基本解， 但基本解不一定是基本可行解。
9
§1 单纯形法的基本思路和原理
2.最优解判别定理
对于求最大目标函数的问题中，对于某个基本可行解，如
果所有检验数 j≤0，则这个基本可行解是最优解。 下面我
们用通俗的说法来解释最优解判别定理。设用非基变量表示
的目标函数为: z z0 j xj jJ 由于所有的xj的取值范围为大于等于零，当所有的 j都小
由线性代数的知识知道，如果我们在约束方程组系数矩阵中找
到一个基，令这个基的非基变量为零，再求解这个m元线性方程组就
可得到唯一的解了，这个解我们称之为线性规划的基本解。
在此例中我们不妨找到
1 1 0 B3 1 0 0
为A的一个基，令这个基的非
1 0 1
基变量x１，s2为零。这时约束方程就变为基变量的约束方程：
第五章 单 纯 形 法

运筹学单纯形法

运筹学单纯形法

单纯形表
max z=x1+2x2 s.t. x1+x23 x2 1 x1, x2 0
Cj CB XB b 0 0 Z X3 3 X4 1 0 1 2 0 0
标准化
max z=x1+2x2 s.t. x1+x2+ x3 =3 x2 +x4=1 x1, x2 ,x3, x40
X1 X2 X3 X4 1 0 1 1 1 2 1 0 0 0 1 0
Z=x1+2x2 x1+x2+ x3 =3 x2 +x4=1 单纯形表
Cj
1
2
0
0
单纯形法原理 单纯形表 CB XB b
z=x1+2x2 x3 =3-x1-x2 x4=1 -x2
x2进基，x4离基
X1 X2 X3 X4

3/1 11
0
1 0
1 1
1 1
2 2 0 1 0 2 0 1 0 0 1 0 -1 0
max z=x1+2x2 s.t. x1+x2+x3 =3 x2 +x4=1 x1, x2, x3, x40
x1=0
(x1,x2,x3,x4)= (0,1,2,0), z=2 C (x1,x2,x3,x4)= (2,1,0,0), z=4,最优解
B
x4=0 x3=0
(x1,x2,x3,x4)= (0,0,3,1), z=0
1 0
0 0
0 1
0
CB XB b 0 2 Z Cj CB XB b 1 2 Z X1 2 X2 1 4 X3 2 X2 1 2 1 1 0 0
X1 X2 X3 X4 1 0 1 1 0 0 0 -1 1 -1

运筹学5-单纯形法

运筹学5-单纯形法

保持可行性 保持可行性 保持可行性
保持可行性
X1
X2
X3
...
Xk
保持单调增 保持单调增 保持单调增
Z1
Z2
Z3
...
保持单调增
Zk
当Zk 中非基变量的系数的系数全为负值时，这时的基 本可行解Xk 即是线性规划问题的最优解，迭代结束。
(2) 线性规划的典则形式
标准型
Max Z CX AX b
s.t X 0
j 1
j 1
j 1
j 1
与X 0 相比，X 1 的非零分量减少1个，若对应的k-1个 列向量线性无关，则即为基可行解；否则继续上述步
骤，直至剩下的非零变量对应的列向量线性无关。
几点结论
❖ 若线性规划问题有可行解,则可行域是一个凸多边形或 凸多面体(凸集),且仅有有限个顶点(极点);
❖ 线性规划问题的每一个基可行解都对应于可行域上的 一个顶点(极点);
10
令 x1 0 x2 0
则 x3 15
X 0 0 15 24T
x4 24
为基本可行解，B34为可行基
B
0
X 24
3
108
A
0
X 34
0
15 24
0
0
X 23
12
45 0
1 基本解为边界约束方程的交点； 2 基对应于可行解可行域极点； 3 相邻基本解的脚标有一个相同。
1 0
1 0
B23 1 0 B24 1 1 B34 0 1
C42
2!
4! 4
2
!
43 21 21 21
6
由于所有|B|≠ 0， 所以有6个基阵和 6个基本解。

运筹学单纯形法

运筹学单纯形法
总结：①在迭代过程中要保持常数列向量非负，这能确保基 可行解旳非负性。最小比值能做到这一点。 ②主元素不能为0。因为行旳初等变换不能把0变成1。 ③主元素不能为负数。因为用行旳初等变换把负数变成1会 把常数列中相应旳常数变成负数。
16
三、其他解旳情况 1、无穷多种解 例2 解LP问题：
min Z x1 2 x2 x3 0 x4 0 x5
xx51
1 2c 5 3c
其中c是满足非负性旳任意常数。
21
再由
x1,
x5
旳非负性，知：
x1 x2
1 2c c
0 0
x5 5 3c 0
解出 0 c 5 3
最优解为：
(2c 1, c,0,0,5 3c)T （其中0 c 5 ）
3
最优值为：max S 1.
22
2、无最优解旳两种情况：
相应地，将 X 0代入目的函数得 Z ( X 0 ) 0
从数学角度看，若让非基变量 x1, x2 取值从零增长，
6
min Z 2x1 x2 0x3 0x4 0x5
相应旳目旳函数值Z也将随之降低。所以有可能找到一种 新旳基本可行解，使其目旳函数值有所改善。即进行基变
换，换一种与它相邻旳基。再注意到 x1 前旳系数－2比 x2
x3
6 x1 x1
2x2 x2
x4 x5
xi 0
i 1,,5
15 24 5
目前可行基{ x3, x4 , x5 }所相应旳基本可行解
X 0 (0,0,15,24,5)T
(相应可行域旳 o(0,0) )
显然不是最优。 因为从经济意义上讲， x1 0, x2 0
意味着该厂不安排生产，所以没有利润。
2

(完整word版)运筹学单纯形法

(完整word版)运筹学单纯形法
0*10+0*20
=0
σj=Cj- Zj
2
-1
1
0
0
0
1
S1
0
0
4
-5
1
-3
0
30
30/4
X1
2
1
-1
2
0
1
0
10
10/-1
S3
0
0
2
-3
0
-1
1
10
10/2
Zj
2
-2
4
0
2
0
Z=Z0=0*30+
2*10+0*10
=20
σj=Cj- Zj
0
1
-3
0
-2
0
2
S1
0
0
0
1
1
-1
-2
10
X1
2
1
0
1/2
0
s.t.
5x1+6x2-4x3-4x4+S1=20
3x1-3x2+2x3+8x4+S2=25
4x1-2x2+x3+3x4+S3=10
x1,x2,x3,x4,S1,S2,S3>=0
迭代次数
基变量
CB
(Ci)
X1
X2
X3
X4
S1
S2
S3
b
比值
bi/aij
6
2
10
8
0
0
0
0
S1
0
5
6
-4
-4
1
0
0
20

运筹学第2章 单纯形法

运筹学第2章 单纯形法

所有检验数 j 0 ，则这个基本可行解是最优解。
n
z z0 j x j
j m 1
m
j ciaij c j =CTBa j c j
i 1
m
m
z0 c j x j = cibi =CBT b
j 1
i 1
✓对于求目标函数最小值的情况，只需 σj≤0
0
XB
b
x1
-1 x5 0
0
0 x4 3
1
-3 0
0
00
x2
x3
x4
0
-2 0
2
-2 1
0 10
-1 bi/aik
x5
1
0
0
29 2020/3/4
2、无界解
在求目标函数最大值的问题中，所谓无界解是指在约束条件 下目标函数值可以取任意的大。
•存在着一个小于零的检验数，并且该列的系数向量的每个元素 都小于或等于零，则此线性规划问题是无界的，一般地说此类
2x1 x2 x3 x5 2
s.t. x1 2x2
x4
3

x1,
x2 , x3, x4 , x5 0
✓添加人工变量x5来人为的创造一个单位矩阵作为基 ✓M叫做罚因子，任意大的数。 ✓人工变量只能取零值。必须把x5从基变量中换出去，否 则无解。
cj
3
2
00
CB XB
2020/3/4
14
(2)出基变量和主元的确定——最小比值规则
min

bi aik
aik

0


bl alk
确定出基变量的方法：把已确定的入基变量在各约束方程中的正的系数

运筹学02-单纯形法

运筹学02-单纯形法

反之，若经过迭代，不能把人工变量都变
为非基变量，则表明原LP问题无可行解。
19
第2章
单纯形法
2.3 人工变量法
2.3.1 大M法
在原问题的目标函数中添上全部人工变量，并令其系数 都为-M，
而M是一个充分大的正数。即
max z = c1x1 + c2x2 + c3x3 + … + cnxn – M( xn+1 + xn+2 +…+ xn+m )
思路：由一个基本可行解转化为另一个基本可行解。 等价改写为 目标方程 max z max z = 3x1+5x2 z -3x1 -5x2 = 0 z -3x1 -5x2 x1 +x3 x1 +x3 = 8 2x2 +x4 2x2 +x4 = 12 s.t. s.t. 3x1+4x2 +x5 3x1 + 4x2 +x5 = 36 x1 ， x2 ，x3，x4，x5 x1 ， x2 ，x3，x4，x5 ≥ 0
以主列中正值元素为分母，同行右端常数为分子，求比值；
6
第2章
单纯形法
2.1 单纯形法的基本思想
(Ⅰ)
用换基运算 将X0 转化为 另一个基本 可行解 X1。
z- 3x1 -5x2 = 0 0 换基运算—— x1 +x3 = 8 ① 方程组的初等变换 目的是把主列变为 22x2 +x4 = 12 ② 单位向量：主元变 3x1 + 4x2 +x5 = 36 ③ 为1，其余变为0。 X0 = ( 0, 0, 8, 12, 36 )T z0 = 0
⑴ 当前基：m阶排列阵

运筹学单纯形法

运筹学单纯形法

第二步：寻求初始可行基，确定基变量
1 2 1 0 0
1 0 0
A


4 0
0 4
0 0
1 0
10
B P3,
P4 ,
P5



0
0
1 0
0 1
对应的基变量是 x3，x4，x5； 第三步：写出初始基本可行解和相应的
目标函数值
两个关键的基本表达式：
写出用非基变量表示基变量的表达式：
由 x4 3 x1 x2 x3 → x1 3 x2 x3 x4
x5 9 x1 4x2 7x3

x5

6

3x2

6x3

x4
得新的基本可行解 X(1)=(3，0，0，0，6)T
⑤ 写出用非基变量表示目标函数的表达式:
Z 2x1 3x2 3x3 2(3 x2 x3 x4 ) 3x2 3x3 6 x2 x3 x4
可得相应的目标函数值为Z(1)=6
检验数仍有正的, 返回①进行讨论。
三、单纯形法的一般描述：
1、初始可行解的确定
(1)初始可行基的确定 观察法——观察系数矩阵中是否含有现成 的单位阵？
于是，若LP只有唯一最优解，这个最 优解所对应的点一定是可行域的一个顶点； 若LP有多个最优解，那么肯定在可行域的 顶点中可以找到至少一个最优解。
转移条件？
转移结果？
使目标函数值得到改善
得到LP最优解，目标函数达到最优值
2．需要解决的问题：
(1)为了使目标函数逐步变优，怎么转移？ (2)目标函数何时达到最优——
要求：

运筹学第2章单纯形法

运筹学第2章单纯形法
==８ ==6
① ② ③
－２Ｘ４＋Ｘ５ ＝１２
得到新的基本可行解 X1 =(0,6,8,0,12)T
(1)、决定进基变量：1=--3, X1进基 (2)、决定离基变量：最小比值规则来确定主 元与离基变量.
则Xl为进基变量。 MIN(8/1,-,12/3)=12/3 此时可以确定X5为离基变量
Z
X(0) =(0, 0, 10, 15 )T
Z0 =0
Z-30X1-20X2 =0 选中X1从0↗，X2 =0 X3=10-(-X1 )0
X4=15-(-3X1 )0 求X1， X1→+ ,Z→+
2.2.3 单纯形法计算之例
2-3 人工变量法 (Artificial Variable)
+1/2X4
+X5 =42 =6
X3 +2/3X4 -1/3X5 =4
X2 +1/2X4
X1 -2/3X4+1/3X5=4 令X4 =X5 =0 X =(4, 6, 4, 0, 0)T Z =42
。此时4=1/2,
Z值不 再增大了,X值是最优基本解
5
=1,
* T * 即:X =(4,6) ,Z =42
检验数
当目标方程中基变量系数全为0时，非基 变量的系数可以作为检验当前的基本可 行解是否最优的标志，称之为检验数。
(2)、判定解是否最优 Z-3X1-5X2 =0 当X1从0↗或X2从0↗ Z从0↗ ∴ X0 不是最优解
(3)、由一个基可行解→另一个基可行解。 ∵ -5<-3 选X2从0↗，X1 =0 X3 =8 X4 =12-2X2 0 X2 12/2
N
沿边界找新 的基本可行解
结束

运筹学一般单纯形法

运筹学一般单纯形法

1
0 0 0 1
0
1 0 0 0
0
0 1 0 -2
3
6 2 →
Cj-Zj
0
2
0
4
x4
x2 →
8
15
3 P1
10 P2
0 P3
0 P4
θi
注
3
-1
4
5
1
0
0
1
段 1 cj-zj
cj ↓ 0 0
→
0
3
10
0
0
基
x3 x4 →
b
24 15
P1
3 -1 3
P2
4 5 10
P3
1 0 0
P4
0 1 0
θi
注
步骤4.2：判断
（１）若所有检验数均≤０时，即得到最优解和 最优值； （２）若检验数存在正值，继续下一步。
3
0 3 1 3
2
（1） 4 0 0
0
0 0 1 0
1
0 0 0 1
0
1 0 -2 -2
6
2 →
Cj-Zj
0 2 0
4
x2
→
2
0
1
0
0
1
Cj-Zj
Cj 段 ↓
→ 基
0 b
3 P1
4 P2
0 P3
0 P4
0 Qi P5 注
0
1 0 0
x3
x4 x5 → x3
6
12 2 0 2
1
3 0 3 1
2
2 （1） 4 0
用主元列对应的变量（入基变量/调入变量）代替之，进入 下一段。

运筹学-单纯形法1课件

运筹学-单纯形法1课件

例2:
cj CB XB 0 x3 0 x4
σj 0 X3 1 x1
σj
maxZ x 1 x 2
s.t.
2x 1 x1
x2 x2
100 50
x1,x2 0
1
1
00
bi x1 x2 x3 x4
100 -2 1
1
0
50 [ 1 ] -1 0 1
11
0
0
200 0 -1 1 2
50 1 -1 0 1
唯一最优解；
• a4<0,a5<0, a6≥0
无穷多最优解；
• a6≥0,a4≤0, a5≤0, a4=0或a5=0
无界；
• a6≥0,a5>0,a2≤0, a3≤0
无可行解；
• a4≤0,a5≤0, x4或x2为人工变量, a6≥0 ；
非最优，继续换基: X3换入，x2换出
• x1为人工变量, a6>0 • a4>0,a4>a5;a6/a1>2→a1>0
0 -M -M
x5 x6 x7 θ
0 0 04 -1 1 0 1
0 0 13
-M 0 0 x2入, x6出
1 -1 0 1 -1 1 0 -
3 -3 1 1
3M -1/2
0 1/2
-4M 0 1/2 -1/2 0 1/3 -1/2 1/6
x1入, x7出 9 3/2
3/2 -M-3/2 -M+1/2 x3入, x1出
28.09.2024
11
练习: 列出初始单纯形表，并求解第2小题 的最优解
P55，2.2（1） 2.
28.09.2024
12
单纯形表

《管理运筹学》求解线性规划的单纯形法

《管理运筹学》求解线性规划的单纯形法

– 基变量在目标函数中的系数为0
– 非基变量在目标函数中的系数<=0.
（注意：目标函数形式 z = 2x1 + 3x2）
– 若目标函数为方程形式：
检验数
z - 2x1 - 3x2=0，则需非基变量的系数>=0
求解线性规划的单纯形法
Q3：如何找下一个相邻的基本可行解
• 迭代步骤1：确定移动的方向
确定进基变量
例：z = 2x1 + 3x2 – 选择 x1 ？Z的增长率=2 – 选择 x2 ？Z的增长率=3 – 3＞2，选择x2！
• 进基变量的选择：
检验数的 绝对值哦
~~~
– 选择非基变量的系数最大的！
求解线性规划的单纯形法
Q3：如何找下一个相邻的基本可行解
• 迭代步骤2：确定在何处停下 – 增加x2 的值， x1 =0
• 选择单元阵作为初始基：
1 1 1 0
A 1
2
0
1


(a1
,
a2
,
a3
,
a4
)
1 0
B


0
1


(a3
,
a4
)
令非基变量 x1= x2 = 0得：X0 = ( 0，0，3，4)T
求解线性规划的单纯形法
Q2：最优性检验
• 非最优：增加非基变量的值，可以使 得目标函数Z值增加
x1,
x2,
x3,
=1 +x4 =2 x4 ≥0
然后确定初始基本可行解
X0 = (0, 0, 1, 2)T z0 = 0
最优性检验：一切σj ≥ 0 ？
当前解 X0 非优； 须由X0 转化为另一个基本可行解 X1。 思路：让X0 中的一个非基变量进基，去替换原来的一个基变量（离基）。
  1. 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
  2. 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
  3. 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
的方案，然后不断去尝试其他的定点，判断其是
否最优，直到找到最优的方案。
School of Information Management ,CCNU
2
《运筹学》
2.1 单纯形法的基本思路：
从可行域中某一个顶点开始，判断此顶点是否是 最优解，如不是,则再找另一个使得其目标函数值更 优的顶点，称之为迭代，再判断此点是否是最优解。
Nx N
11
《运筹学》
B -1 Bx B + B -1 Nx N = B -1b Þ x B + B -1 Nx N = B -1b
Þ x B = B -1b - B -1 Nx N
令xN = 0
x B1 x B2
Bb-11 b1 = Bb-21b2
x Bm
Bb-m1 b m
B -1 Bx B = Ex B = x B
定理1
D = { x Î R n | Ax = b , x ³ 0 } 是 凸 集 .
证 任 取 x , y Î D ， w = l x + (1 - l ) y ， 其 中
l Î [0 ,1]. 由于 x ³ 0， y ³ 0，故w ³ 0. 又 Ax = b ， Ay = b ， 故
Aw = l Ax + (1 - l ) Ay = b
顶 点
School of Information Management ,CCNU
8
《运筹学》
从图解法的几何直观容易得到下面两个重要结论：
⑴．线性规划的可行区域D是若干个半平面的 交集， 它形成了一个有界的或无界的凸 多边形.
⑵．对于给定的线性规划问题，如果它有最优 解，最优解总可以在D的某个顶点上达到.
B -1 Nx N
School of Information Management ,CCNU
12
《运筹学》
xB = B -1b xN = 0
é B -1bù x=ê ú
êë 0 úû
基本解
x B1 x B2
若 B -1b ³ 0 则 x ³ 0
x 基本可行解 B 可行基
B -1b1 B -1b2
即wÎ D.
School of Information Management ,CCNU
6
《运筹学》
定理2 任意多个凸集的交还是凸集. 证 如果 x 和 y 是 I Si中的两个点，则 x 和 y 必
属 于 每 一 个 Si ，因 此 它 们 的 凸 组 合 也 在 每 一 个 Si里，从而也在I Si里.
bm
School of Information Management ,CCNU
10
《运筹学》
A = (B,N )
x
=
çæ çè
xB xN
÷ö ÷ø
Ax = b
(B
N
)ççèæ
xB xN
÷ö ÷ø
=
b
Þ Bx B + Nx N = b
b1 b2 =
bm
Bx B
School of Information Management ,CCNU
School of Information Management ,CCNU
7
《运筹学》
定义2
设 S 为 凸 集 ， x Î S .若 对 任 何 y Î S ，z Î S ， y ¹ z，以及任何0 < l < 1，都有
x ¹ ly + (1 - l )z
则 称 x 为 凸 集 S 的 一 个 顶 点 (极 点 ).
中与之对应的 m 个分量称为基变量，其余的分
量 称 为 非 基 变 量 .令 所 有 的 非 基 变 量 取 值 为 零 ，
é xB ù é B -1bù
得到的解 x = ê ú = ê
ú，称为相应于 B 的
êë x N úû êë 0 úû
基本
解
.当
B
-1b
³
0 时
，称
基本
解
x
为基本可行
解，这时对应的基B 称为可行基.
School of Information Management ,CCNU
9
《运筹学》
(2)基本可行解及线性规划基本定理
Ax = b 秩 ( A ) = m , m < n a11 x1 a12 x 2 a 21 x1
am1 x1 am 2 x2
a1n xn
b1
a2n xn =
b2
a mn x n
考虑标准形式的LP问题
m ax cTx
s
.t
.
ìï A
í ïî
x
x ≥
= 0
b
x Î R n ,c Î R n ,b Î R m , A Î R m´n
设 D = { x Î R n | Ax = b , x ³ 0} ¹ f
秩(A) = m,m < n
School of Information Management ,CCNU
第二章 单 纯 形 法
2.3 单纯形法的基本证明
School of Information Management ,CCNU
1
《运筹学》
n 由于图解方法只能解决两个决策变量的线性规划 问题，因此对于多个决策变量的线性规划问题就
无法解决； n 图解法作图难以规范； n 图解法中：总是从某个顶点开始，给出一个初始
直到找到一个顶点为其最优解，就是使得其目标函数
值最优的解，或者能判断出线性规划问题无最优解为
止。
由此可见，这里必须要解决三个问题
1）找到一个初始可行解. 2）如何判断是否是最优解 3）如果不是，如何改进（迭代）
School of Information Management ,CCNU
3
《运筹学》
线性规划问题的可行域
4
《运筹学》
定义1
设 S Ì R n 是n 维欧氏空间中的一个点集，若对任 何 x Î S , y Î S 与任何l Î [0,1]，都有
lx + (1 - l ) y Î S
就称S 是一个凸集.
凸集
极点
School of Information Management ,CCNU
凸集
5
《运筹学》
不是凸集
School of Information Management ,CCNU
14
《运筹学》
定理3
可行解 x 是基本可行解的充要条件是它的正分量所
对应的 A 中列向量线性无关.
证：不妨设 x的前 k 个分量为正分量，即
x = ( x1 ,Lformation Management ,CCNU
13
《运筹学》
B -1bm
定义3
设 B 是 秩 为 m 的 约 束 矩 阵 A Î R m´n 中 的 一 个
m 阶 满 秩 子 方 阵 ， 则 称B 为 一 个 基 (或 基 阵 ). B
中m个线性无关的列向量称为基向量，变量 x