- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
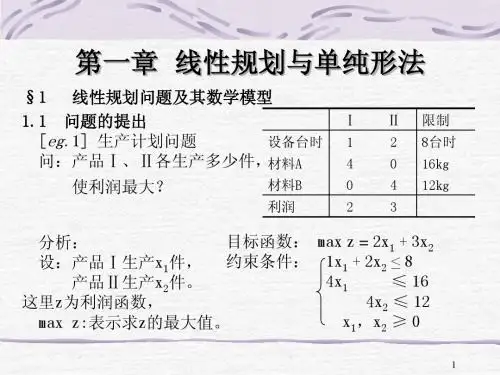
假定在市场上可买到 B1,B2,…Bn n 种食品,第 i 种
食品的单价是 ci , 另外有 m 种营养 A1,A2,…Am。设 Bj
内含有 Ai 种营养数量为 aij (i=1~m,j=1~n),又知人们每
天对 Ai 营养的最少
表2
需要量为 bi。见表2:
食品
最少
试在满足营养要 求的前提下,确定食 品的购买量,使食品 的总价格最低。
则 A = ( B, N )
§3 线性规划问题解的基本性质
A = ( B, N )
xB= (x1,…,xm)T , xN =(xm+1,…,xn)T
则
x
xB xN
,
代入约束方程(2),得
B
N
xB xNLeabharlann b.BxB Nxn b
xB B1b B1NxN
自由变量 (独立变量)
令 xN 0 xB B1b
c c1, c2, , cn 价值向量 x x1, x2, , xn T 决策向量
什么意思? 为什么?
b b1, b2 , , bm T , bi 0 右端向量
第一章 线性规划及单纯形法
定义 3 在上述 LP 问题中,约束方程组(2)的系数 矩阵 A 的任意一个 m×m 阶的非奇异的子方阵 B (即 |B|≠0),称为 LP 问题的一个基阵或基。
x2
max z = 2x1 + 2x2 s.t. 2x1 – x2 ≥ 2
-x1 + 4x2≤ 4 x1,x2 ≥ 0
(1,0)
O
A
2x1 x2 2
x1 4x2 4
x1
Note: 可行域为无界区域, 目标函数值可无限 增大,即解无界。 称为无最优解。
§2 线性规划问题的图解法
由以上两例分析可得如下重要结论:
线性规划问题的标准形式:
max z = c1x1 + c2x2 + … + cnxn s.t. a11x1 + a12x2 + … + a1nxn = b1
a21x1 + a22x2 + … + a2nxn = b2 …… am1x1 + am2x2 + … + amnxn = bm
xj ≥ 0 (j = 1,2,…,n) bi ≥ 0 (i = 1,2,…,m)
运筹学
Operations Research
第一章 线性规划及单纯形法
第一章 线性规划及单纯形法
线性规划(Linear Programming,简称LP) 运筹学的一个重要分支,是运筹学中研究较早、发展较 快、理论上较成熟和应用上极为广泛的一个分支。
1947年G.B. Dantying提出了一般线性规划问题求解 的方法——单纯形法之后,线性规划的理论与应用都得 到了极大的发展。
1、善于抓住关键因素,忽略对系统影响不大的因素; 2、可以把一个大系统合理地分解成 n 个子系统处理。
三个基本要素:
1、决策变量 xj≥0 2、约束条件 —— 一组决策变量的线性等式或不等式 3、目标函数 —— 决策变量的线性函数
第一章 线性规划及单纯形法
线性规划问题的一般形式:
max(min)z = c1x1 + c2x2 + … + cnxn s.t. a11x1 + a12x2 + … + a1nxn ≤(或=,≥)b1
§2 线性规划问题的图解法
绿色线段上的所有点 都是最优解,即有无穷多 最优解。Zman=34.2
x1 + 1.9 x2 = 11.4
x2
(3.8,4)
max z =3x1 + 5.7x2 s.t. x1 + 1.9x2 ≥ 3.8
x1 - 1.9x2≤ 3.8 x1 + 1.9x2 ≤11.4 x1 - 1.9x2 ≥ -3.8
最多有
Cnm
=
n! m!(n-m)!
种
定义 4 在LP问题的一个
基可行解中,如果它的所
Rn
非可行解
基 可行解 可 基解
行 解
有的基变量都取正值,则
称它是非退化的解;反之,如果有一个基变量也取
甲
A
1
B
1
单件利润 15
乙 库存量
3
60
1
40
25
x1,x2 ≥ 0 目标函数:
z = 15 x1 +25 x2
Subject to
max z = 15x1 +25x2 s.t. x1 + 3x2 ≤ 60
x1 + x2 ≤ 40 x1,x2 ≥ 0
§1 线性规划问题及其数学模型
e.g. 2 营养问题
x1,x2 ≥0 化为标准形式。
解: 令 x3= x4 - x5 其中x4、x5 ≥0;
对第一个约束条件加上松弛变量 x6 ;
对第二个约束条件减去松弛变量 x7 ;
对第三个约束条件两边乘以“-1” ;
令 z’=-z 把求 min z 改为求 max z’
§1 线性规划问题及其数学模型
LP的几种表示形式:
n
即化为: max z ' c j x j j 1
2、约束条件为不等式,
xn+1 ≥ 0
松弛变量
n
aij x j bi j 1
n
aij x j bi j 1
n
aij x j xn1 bi
j 1
如何处理?
§1 线性规划问题及其数学模型
3、右端项bi < 0时,只需将等式两端同乘(-1)
x1 ,x2 ≥ 0
x1 - 1.9 x2 = -3.8
(0,2)
D可行域
(7.6,2)
max Z
min Z o
(3.8,0)
x1 + 1.9 x2= 3.8 0=3 x1 +5.7 x2
x1 - 1.9 x2 = 3.8 34.2 = 3 x1 +5.7 x2
x1
第一章 线性规划及单纯形法
可行域为无界 区域一定无最 优解吗?
B1b
x
0
(4) 称(4)为相应于基 B 的基本解
第一章 线性规划及单纯形法
B1b x (4)
0
是可行解吗?
max 3x5
z’= x1-2x2+3x4-
s.t. x1+x2+x4-x5+x6=7
x1-x2+x4-x5-x7=2
3x1-x2-2x4+2x5=5
1 1 1 1 1 0
z cx (1)
Ax b (2)
x0
(3)
z cx
n
pjxj b j 1
x0
x x1, x2 ,, xn T 决策向量
b b1 , b2 ,, bm T , bi 0 右端向量
p j a1 j , a2 j ,, amj T 为A的第j列向量
§2 线性规划问题的图解法
max z cx
60年来,随着计算机的发展,线性规划已广泛应用 于工业、农业、商业、交通运输、经济管理和国防等各 个领域,成为现代化管理的有力工具之一。
§1 线性规划问题及其数学模型
e.g. 1 资源的合理利用问题
某工厂在下一个生产周期内生产甲、乙两种产品,
要消耗A、B 两种资源,已知每件产品对这两种资源
的
消耗,这两种资源的现有数量和每件产品可获得的利 表1
1、LP 问题从解的角度可分为:
⑴ 有可行解
a. 有唯一最优解
b. b. 有无穷多最 优解
⑵ 无可行解 c. C. 无最优解
2、LP 问题若有最优解,必在可行域的某个顶点上取
到;若有两个顶点上同时取到,则这两点的连线上
任一点都是最优解。
§2 线性规划问题的图解法
图解法优点: 直观、易掌握。有助于了解解的结构。
max s.t.
n
z c j x j j 1
n
aij x j bi (i 1,2,, m)
j 1
x j 0 ( j 1,2,, n)
a11
A
a21
a12
a22
a1n
a2n
系数矩阵
am1 am2 amn
c c1, c2, , cn 价值向量
max s.t.
max s.t.
x1 + x2 ≤ 40 x1,x2 ≥ 0
x1 x2 40
A (0,20)
(0,0) O
B (30,10)
x1 3x2 60
C (40,0)
Z=250
L2
最优解:
x1=30 x2 =10
最优值:zmax=700
x1
L1
第一章 线性规划及单纯形法
LP问题图解法的基本步骤:
1、在平面上建立直角坐标系; 2、图示约束条件,确定可行域和顶点坐标; 3、图示目标函数(等值线)和移动方向; 4、寻找最优解。
对任意的x∈D 都有c x*≥c x,则称x*为LP 问题
的最优解,相应的目标函数值称为最优值,
记作 z*=c x*。
§2 线性规划问题的图解法 目标函数变形:
max z = 15x1 +25x2 s.t. x1 + 3x2 ≤ 60
x2=-3/5 x1+z/2B5点是使z达到最
大的唯一可行点
x2
特点:
1、目标函数为极 大化; 2、除决策变量的 非负约束外,所有 的约束条件都是等 式,且右端常数均 为非负;
3、所有决策变量 均非负。
第一章 线性规划及单纯形法