下载文档原格式
械图样。
（二）三视图的形成与投影规律（用怎样才能完整表达物体各个面形状和书上图1-5引入：看物体至少需从几个方面看？）假设投影线为平行且垂至于投影面的投影线，这样在投影面上所得到的正投影称为视图。
问：什么叫视图？提出问题：1、三投影面分别指的是那三面？2、以教室墙角为例讲解V、H、W3、讲解撒头面相交所得到的轴和原点1、三投影面体系与三视图的形成（1）三投影面体系的建立由三个互相垂直的投影面所组成，如图所示。
正立投影面：简称为正面，用V表示；水平投影面：简称为水平面，用H表示；侧立投影面：简称为侧面，用W表示。
他们的交线称为投影轴。
OX轴、OY轴、OZ轴：交点称为原点O（2）三视图的形成演示：一边用简单道具粉笔盒演示投影一边讲解每个投影的名称，和每个视图的名字，并要求学生记住将物体放在三投影面体系中，将物体对各个投影面进行投影，得到三个视图，主视图：从前往后进行投影，在正立投影面（V面）上所得到的视图。
俯视图：从上往下进行投影，在水平投影面（H面）上所得到的视图。
主视图：从前往后进行投影，在侧立投影面（W面）上所得到的视图。
（3）三投影面体系的展开提示学生假想：利用空间想象能力假想V、W面分别绕X、Y轴展开后三个视图的位置的情况）总结：俯视图在主视图的正下方，左视图在主视图的正右方。
2、三视图的投影规律问：A、主视图反应物体的那两个尺寸？B、俯视图反应物体的哪两个尺寸？C 、左视图反应物体的那两个尺寸？引导：主视图和俯视图什么相等？主视和左视什么相等？俯视和左视什么相等？么投影法？6、学生跟随老师引导和根据书上的图1-5分析讨论回答：要表达清楚一个零件的形状至少需要从几个方面看？7、学生随老师提问快速看书预习，并随老师引导回答？A、三投影面指的是那三面？B、三投影面分别应该用什么字母表示？C、三投影面相交分别得到了什么轴？8、学生认真观察，思考记忆每个投影面的投影名称9、学生思考，利用空间想象能力假想（也可以用自制纸壳演示VW沿XY展开后的位置关系，并回答10、学生回答每个视图反应那两个尺寸让学生在老师的引导下，能够逐步的学会自己思考问题，分析问题，解决问题让学生能够迅速的掌握重点知识让学生自己观察讨论得出结论，有利于学生对该知识点的掌握培养激发学生学习兴趣结论：“长对正”（即等长）；“高平齐”（即等高）；宽相等”（即等宽）；3、三视图与物体方位的对应关系演示：用一简单的教具粉笔盒为大家演示每个视图所表达的方位？物体有长、宽、高三个方向的尺寸，有上下、左右、前后六个方位关系，如图（a）所示。
三视图的形成及其投影规律用正投影法绘制出物体的图形称为视图。
一个视图只能反映物体的一个方位的形状。
不能完整反映物体的结构形状。
三视图是从三个不同方向对同一个物体进行投射的结果。
能较完整的表达物体的结构。
一、三视图的形成1. 三投影面体系三投影面体系由三个相互垂直的投影面和三条投影轴（立体坐标）构成正立投影面简称正面代号V三个投影面水平投影面简称水平面代号H侧立投影面简称侧面代号WV与H的交线称为OX轴简称X 轴它代表物体的长度方向三条投影轴W与H的交线称为OY轴简称Y 轴它代表物体的宽度方向W与V的交线称为OZ轴简称Z 轴它代表物体的高度方向X、Y、Z三轴的交点O 称为原点2. 三视图的形成过程和名称从物体的前面向后面投射，在V 面所得的视图称主视图—能反映物体的前面形状从物体的上面向下面投射，在H 面所得的视图称俯视图—能反映物体的上面形状从物体的左面向右面投射，在W 面所得的视图称左视图—能反映物体的左面形状3. 三视图的展开及其位置三视图的展开以V面为基准，沿Y 轴剪开，然后H 面绕X轴向下转90°W面绕Z轴向右转90°三视图的位置主视图在图纸的左上角左视图在主视图的正右方俯视图在主视图的正下方二、三视图之间的投影关系（三等关系）任何物体均有长、宽、高三个方向尺寸，该关系是用于分析每一视图如何反映物体的这些尺寸。
分析的前提必须先规定物体的长、宽、高尺寸方向。
强调正对主视图（V面）的水平方向为物体的长度方向，然而，其宽度和高度方向就自然地确定下来了。
主视图反映物体的长高尺寸；不反映宽尺寸。
（原因：宽方向与主视的投射方向重合）俯视图反映物体的长宽尺寸；不反映高尺寸。
（原因：高方向与俯视的投射方向重合）左视图反映物体的高宽尺寸；不反映长尺寸。
（原因：长方向与左视的投射方向重合）由此可见：1、每一视图只能反映物体两个方向的尺寸。
2、每两个视图反映的相同方向尺寸，具有尺寸等量的内在联系。
基本立体基本体其表面几何形状不同分为：平面立体和曲面立体。
所有表面由平面围成的立体称为平面立体，常见的有棱柱体和棱锥体；表面由曲面或者曲面和平面围成的立体称为曲面立体，常见的有圆柱体、圆锥体、圆球和圆环等。
三视图的形成及投影规律两个形状不同的物体在同一投影面上的投影却会相同。
因此由一个投影不能确定物体的形状解决办法：增加投影面。
一、三视图的形成空间分析：如图 a 所示，把物体放在三投影面体系中，按正投影法向三个投影面投射，可以分别得到物体的正立投影面投影、水平投影面投影和侧立投影面投影。
在工程图样中这种投影叫做“视图”。
主视图——由前向后投射，在正立投影面（简称正面）上所得到的视图；俯视图——由上向下投射，在水平投影面上所得到的视图；左视图——由左向右投射，在侧立投影面（简称侧面）上所得到的视图。
展开：如图所示。
投影面V 面不动，将H 面和W 面分别绕OX 轴和OY 轴按图示方向旋转90°，使它们展开成与V 面处在同一平面上，如图 b 所示。
在投影图中不画投影面的边框线，形成的三个视图如图 c 所示。
（a）物体的投影 (b)展开图（c）三视图三视图的形成二、三视图的投影规律从三视图形成过程中可以看出，三个视图之间存在一定的位置关系，即以主视图为准，俯视图在主视图的正下方，左视图在主视图的正右方。
由此可以归纳出在画物体三视图时，三个视图之间存在如下投影关系：主、俯视图长对正；主、左视图高平齐；俯、左视图宽相等。
三、三视图代表的方位在空间，物体有长、宽、高三个方向的尺寸。
如果规定物体沿X 方向上的左右距离称为长，沿Z 方向的上下距离称为高，沿Y 方向的前后距离称为宽，则一个视图能反映物体的两个方向的尺寸。
即：主、俯视图同时反映出物体左右方向上的长度尺寸，长度相等；主、左视图同时反映了物体上下方向上的高度尺寸，高度相等；俯、左视图同时反映了物体前后方向上的宽度尺寸，宽度相等。
立体图视图投影规律和方位对应关系四、三视图的画法举例例：绘制图示物体的三视图。
2-1 投影法与三视图物体在光线照射下，在地面或墙壁上产生影子。
人们对这种自然现象加以抽象研究，总结其中规律，创造了投影法。
所谓投影法，就是投射线通过物体，向选定的平面（投影面）投影，并在该平面上得到图形（投影图）的方法。
投影法分为两大类：中心投影法和平行投影法。
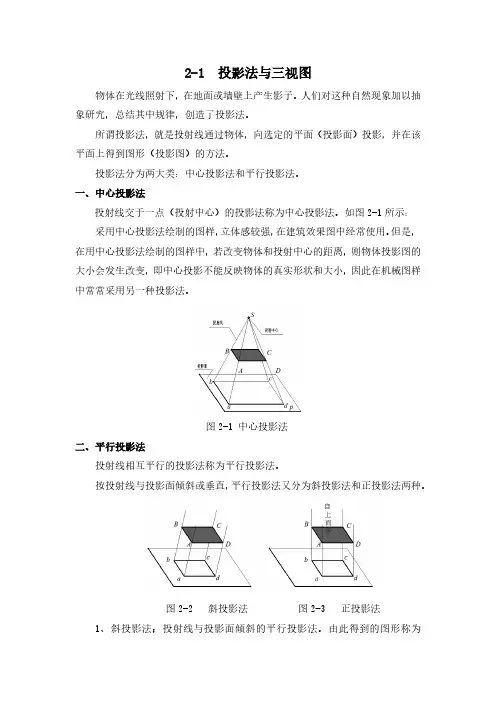
一、中心投影法投射线交于一点（投射中心）的投影法称为中心投影法。
如图2-1所示：采用中心投影法绘制的图样，立体感较强，在建筑效果图中经常使用。
但是，在用中心投影法绘制的图样中，若改变物体和投射中心的距离，则物体投影图的大小会发生改变，即中心投影不能反映物体的真实形状和大小，因此在机械图样中常常采用另一种投影法。
图2-1 中心投影法二、平行投影法投射线相互平行的投影法称为平行投影法。
按投射线与投影面倾斜或垂直，平行投影法又分为斜投影法和正投影法两种。
图2-2 斜投影法图2-3 正投影法1、斜投影法：投射线与投影面倾斜的平行投影法。
由此得到的图形称为斜投影图（简称斜投影）。
如图2-2所示。
2、正投影法：投射线与投影面垂直的平行投影法。
由此得到的图形称为正投影图（简称正投影）。
如图2-3所示。
正投影图度量性好，作图简单，机械图样常常采用正投影法绘制。
三、正投影的基本特性(单投影面)1、真实性：当物体上的平面（或直线）与投影面平行时，其投影反映实形（或实长）。
如图2-4(a)。
2、积聚性：当物体上的平面（或直线）与投影面垂直时，其投影积聚成直线（或点）。
如图2-4(b)。
3、类似性（亦称收缩性）：当物体上的平面（或直线）与投影面倾斜时，其投影收缩成原来形状的类似形。
如图2-4(c)。
图2-4 正投影的特性四、三视图的形成及投影规律1、三投影面体系一般情况下，物体的一个投影图（二维）不能准确地反映物体（三维）的完整形状，如图2-5所示。
要想准确表达物体的结构形状，就必须增加投影图。
工程上常采用在三投影面体系中得到的三面投影图来表达物体的形状，如图2-6所示。
