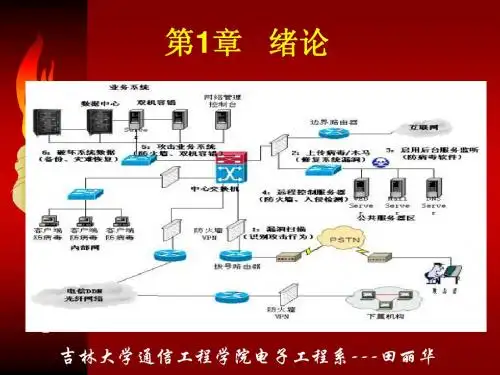
纠错编码技术第一章绪论

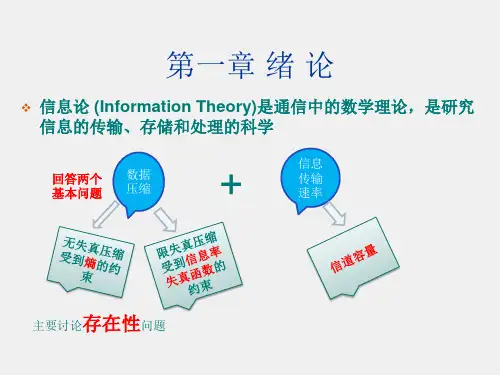
信息论复习提纲第一章绪论1．通信系统模型；2．香浓信息的概念；3．信源、信道、信源编码和信道编码研究的核心问题。

第二章离散信源及信源熵1．离散信息量、联合信息量、条件信息量、互信息量定义；2．信源熵、条件熵、联合熵定义；3．平均互信息量定义、性质、三种表达式及物理意义，与其它熵的关系（不证明）；4．最大信源熵定理及证明；5．本章所有讲过的例题；第三章离散信源的信源编码1．信息传输速率、编码效率定义；2．最佳编码定理（即节定理：概率越大，码长越小；概率越小，码长越大）及证明；3．码组为即时码的充要条件；4．单义可译定理（Kraft不等式）及应用；5．费诺编码方法、霍夫曼编码方法应用（二进制，三进制，四进制）；6．本章所有讲过的例题；第四章离散信道容量1．利用信道矩阵计算信道容量（离散无噪信道、强对称离散信道、对称离散信道、准对称离散信道）；2．本章讲过的例题；第五章连续消息和连续信道1．相对熵的定义；2．均匀分布、高斯分布、指数分布的相对熵及证明；3．峰值功率受限条件下的最大熵定理及证明，平均功率受限条件下的最大熵定理及证明，均值受限条件下的最大熵定理及证明；4．香农公式及意义；5．本章所有讲过的例题；第六章差错控制1．重量、最小重量、汉明距离、最小汉明距离、编码效率的定义；2．最小距离与检错、纠错的关系（即节定理）；3．本章所有讲过的例题；第七章线性分组码1．线性分组码定义；2．线性分组码的最小距离与最小重量的关系及证明；3．生成矩阵、一致校验矩阵定义，给出线性方程组求出生成矩阵和一致校验矩阵的标准形式，生成矩阵与一致校验矩阵的关系；4．制作标准阵列并利用标准阵列译码；5．本章所有讲过的例题；第八章循环码1．生成多项式的特点，有关定理（三定理1，定理2，定理3）及证明；2． 生成矩阵、一致校验矩阵定义，如何获得生成矩阵、一致校验矩阵的典型形式；3．本章所有讲过的例题； 习题：1.已知随机变量X 和Y 的联合分布如下：计算：、I(X;Y)。

《纠错编码技术》课程教学大纲课程编码：课程名称：纠错编码技术课程类型：学时分配：32学分：适用对象：通信工程，信息工程，电子信息工程先修课程：通信原理一、课程性质、目的和任务本课程是为通信工程专业（信息工程专业，电子信息工程专业）本科生设立的学科基础课。

本课程的目的是让学生了解纠错编码的基本原理、特性和设计方法，掌握线性分组码、循环码和卷积码的基本原理、特性以及编译码的方法。

教学任务有：纠错编码的基本概念、分类和性能评价；纠错编码代数基础；线性分组码的定义，生成矩阵、校验矩阵，编码的实现，译码的方法；循环码的定义，循环码的多项式描述，循环码的生成矩阵、生成多项式和监督矩阵，循环码的编码与译码；卷积码的数学描述，卷积码的图形描述，Viterbi译码。

本课程配有实验教学，采用MATLAB编程或SIMULINK模型搭建来实现编码，并通过实验验证编码对通信系统性能的改善，以达到巩固所学知识，加深理解理论教学的目的。

二、教学内容第一章纠错编码的基本概念1.1纠错编码的理论基础1.2纠错编码的分类1.2.1差错控制编码的分类1.2.2差错控制系统分类1.2.3纠错编码的分类1.3纠错编码的基本定义1.4有噪信道编码定理1.5译码规则和编码规则1.5.1错误概率1.5.2译码规则1.5.3平均错误概率1.5.4信道编码的编码原则1.6纠错编码的本质1.7纠错编码方法的性能评价1.8纠错编码系统的性能第二章纠错编码代数基础2.1整数的有关概念2.1.1整数的概念及性质2.1.2同余和剩余类2.1.3多项式2.2群的基本概念2.2.1群的定义2.2.2循环群2.2.3子群和陪集2.3环的基本概念2.3.1环的定义2.3.2环的性质2.3.3子环2.3.4剩余类环2.4域的基本概念2.4.1域的定义2.4.2有限域2.4.3二元域的运算第三章线性分组码3.1线性分组码的定义3.2生成矩阵和校验矩阵3.2.1生成矩阵3.2.2校验矩阵3.3系统线性分组码3.4对偶码3.5编码的实现3.6线性分组码的译码3.6.1信息传输系统模型3.6.2标准阵列3.6.3译码及纠错能力3.7汉明码3.7.1汉明码的构造3.7.2汉明限与完备码3.8线性分组码的编码实现与仿真3.8.1从码元符号与信息符号的关系得到生成矩阵3.8.2从码元符号与信息符号的关系得到校验矩阵3.8.3生成矩阵与校验矩阵的相互转换3.8.4将非标准的生成矩阵转换为标准的生成矩阵3.8.5 线性分组码编译码得的实现（多种方法）3.8.6 Simulink仿真第四章循环码4.1循环码的定义4.2循环码的多项式描述4.2.1循环码的多项式4.2.2码多项式的按模运算4.3循环码的生成矩阵、生成多项式和监督矩阵4.3.1循环码的生成矩阵4.3.2循环码的生成多项式4.3.3循环码的监督多项式和监督矩阵4.4循环码的编码与译码4.4.1循环码的编码4.4.2电路实现4.4.3循环码的译码4.4.4循环码的检错能力4.5 BCH码4.5.1 BCH码的基本概念4.5.2 BCH码的生成4.5.3 BCH码的译码4.6 RS码4.7循环码的编码实现与仿真4.7.1循环码编译码实现（多种方法）4.7.2 Simulink仿真第五章卷积码5.1卷积码的基本概念5.2卷积码的编码过程5.3卷积码的数学描述5.3.1卷积码的码多项式法描述5.3.2卷积码的矩阵生成法描述5.3.3卷积码的离散卷积法描述5.4卷积码的图形描述5.4.1状态图5.4.2树图5.4.3网格图5.5Viterbi译码5.5.1Viterbi译码步骤5.5.2Viterbi译码过程5.6卷积码举例5.7卷积码的编码实现与仿真5.7.1卷积码编码实现（多种方法）5.7.2 Viterbi译码5.7.3 Simulink仿真三、课程学时数安排四、实验1．线性分组码的编码实现及性能仿真（2学时）2．循环码的编码实现及性能仿真（2学时）五、考核方式课程采用开卷考试或大作业的形式。

Reed-Solomon编译码算法研究与硬件实现的开题报告一、研究背景在通信、储存等领域中，数码信号可以因干扰、噪声、失真等原因发生损伤，进而影响到系统的性能和可靠性。

纠错编码技术是保证数字信号传输可靠性的重要技术。

其中，Reed-Solomon编译码算法是一种常用的前向纠错编码算法，被广泛应用于数据通信、数字广播、光纤通信等领域。

二、研究内容本论文主要研究Reed-Solomon编译码算法的理论介绍、编码过程、解码过程和实现方法，以及其在硬件系统中的实现。

具体内容包括：1. 确定编码与解码算法的参数，包括码长、校验位数、生成多项式、主元多项式等。

2. 介绍Reed-Solomon编码的基本原理、编码过程和解码过程，重点介绍单错误纠正、多错误纠正的解码方法。

3. 研究Reed-Solomon编码在FPGA硬件系统中的实现方法，包括设计与确定硬件架构、调试和验证等步骤。

4.设计验证平台，通过仿真验证和实验测试验证Reed-Solomon编码算法和硬件实现的正确性和可靠性。

三、研究意义Reed-Solomon编译码算法作为一种前向纠错编码算法，在通信、储存等领域中被广泛使用，并且具有很强的容错性。

本文的研究将有助于加深对该算法的理解和应用，为其在实际工程中的实现提供参考。

另外，硬件实现方法的研究也提高了编码速度，可以更好地适应实时性要求较高的场景，进一步提高了系统的性能和可靠性。

四、研究方法1. 理论分析法：通过对Reed-Solomon编译码算法进行理论分析和比较，研究其优缺点及适用场景。

2. 外文文献法：查阅相关英文文献，进行文献综述和翻译，获取最新的研究进展和应用案例。

3. 实验分析法：基于FPGA硬件开发平台，结合Verilog HDL语言，实现Reed-Solomon编译码算法的硬件系统，验证其性能和可靠性。

五、预期结果1. 深入理解Reed-Solomon编译码算法的原理和应用场景，对比各种算法的优劣，选择合适的参数进行编码与解码。

第1章绪论本章教学基本要求：掌握：1. 通信基本概念2. 信息量、主要性能指标计算3. 数字通信系统的组成理解：1. 通信系统的分类2. 通信系统的发展本章核心内容：一、通信的基本概念二、通信系统的组成、分类三、数字通信系统的性能指标四、数字通信技术及发展一、通信的基本概念1. 通信：消息传递的全过程，即信息的传输与交换。

2. 消息：是有待于传输的语言、活动图片和文字、数据等。

3. 信息：消息中包含的有意义的内容。

4. 信号：信息的物质载体。

5. 信息量：度量信息多少的量值，它和消息的总类，消息的重要程度无关，它只反应一个量值。

1）信息量的计算消息中所含信息量与消息出现的概率有关。

（1）信息量（I ）是消息出现的概率（P(x)）的函数：I=I[P(x)] （2）消息出现的概率愈小，它所包含信息量愈大；反之信息量愈小。

且P(x)=1时，I=0，P(x)=0时，I=（3）若干个互相独立事件构成的消息，所含信息量等于各独立事件信息量的和。

I[P(x 1)P (x 2)…P(x n )] = I[P(x 1)]+ I[P(x 2)]+…+ IP(x n )]所以，I=log a)(1x p = - log a p(x) 信息量I 的单位与对数的底数有关：当对数底a 取2时，信息量的单位为比特（bit ）；当对数底a 取e 时，信息量的单位为奈特（nit ）；当对数底a 取10时，信息量的单位为哈特（hart ）。

通常使用的单位为比特。

1比特（bit ）的含义：是信息量的度量单位；一位二进制数不经压缩所含的信息量；一个脉冲波形所含的信息量；一比特等于488微秒。

2）离散信源的平均信息量（1）离散等概时信息量的计算假设有M(M=2K )个消息，它们是等概的，每条消息的概率P(x)=M1，以2为底时：I=lb)(1x P =lbM=K(bit) （2）离散不等概时信息量的计算某离散信息源输出x 1,x 2,…,x M M 个不同符号，它们出现的概率分别为P(x 1),P(x 2),…,P(x M )。

本科生毕业论文（设计）中文题目Turbo码在第三代移动通信中应用英文题目学生姓名班级学号学院专业指导教师职称摘要Turbo码是应用在CDMA2000系统中的新的纠错编码技术。

自从被提出之后，已经从最初的理论研究，发展到成功的应用到第三代移动通信系统当中。

Turbo码的纠错性能优于卷积编码，但是译码复杂度高，而且编码时延较大，适用于对时延要求不高的高速数据业务。

本文主要介绍了Turbo码的产生背景，研究现状以及应用的领域。

掌握了Turbo码编码器的结构和译码器的原理。

在无线通信系统中，无线信道的特性对信号传输的影响非常大，本文介绍了无线信道的特性，信道衰落的产生的原因以及CDMA2000系统的空中接口的物理信道，引出了在信道纠错编码领域中一项就有突破性意义的技术，即Turbo码技术。

Turbo不仅在信道编码领域凸显出其优异的性能，基于Turbo码的基本思想，尤其是迭代译码的思想，Turbo码与其他技术结合时，可以对整个系统提供更好的性能。

还介绍介绍Turbo码在cdma2000中的应用仿真，并对它的性能进行了分析以及在设计Turbo的相关参数时应该注意的问题。

最后对本毕业设计做了简要总结及致谢。

关键词Turbo码编码译码CDMA2000ABSTRACTTurbo code is an error correctioncoding techniquesusedintheCDMA2000 system. Since the turbo code was proposed,turbo code has been applied in the third generation mobile communicaton system successfully.Error correction performanceofTurbo codeis better thantheconvolutional encoding.Becauseturbo code’s decoding is high complexityandcodingdelayis long ,it is fit fordelaylow-speed data services.This paper describes the backgroundofTurbo codes, and its theareasofcurrent researching andapplications. I learn theprincipleofthe structureoftheTurbo Encoderanddecoder. Inwireless communication systems, radio channelcharacteristics ofthesignal transmissionis very large.This article describes thecharacteristicsofthewireless channel, thechannel fadingcauses andCDMA2000air interfacephysicalchannel.There isabreakthroughtechnologyinthefieldofthe channelerror correction coding. Not only Turbo codereflectsexcellent performanceinthefieldofchannel coding, especiallytheideaofiterative decodingbasedonthe basic ideaofTurbo codes, but also Turbocodes andothertechnologiescanprovide better performancein the entire system.This articlealso describestheapplicationofTurbo codesin cdma2000simulation,and makesperformanceanalysis, anddiscibe what theproblemshould be noted when peopledesigntheTurbo. Finally, I made a briefsummaryandthanks inthis graduation.Keywords Turbo-code Coding decoding CDMA2000system目录第一章绪论11.1 第三代移动通信11.2 Turbo码的起源11.3 Turbo码研究现状21.4 Turbo码的应用领域3第二章Turbo码编译码原理62.1 编码原理62.2 分量编码器和删余器72.3 交织器92.4 解码原理112.5 解码算法132.6 小结19第三章Turbo码在CDMA2000中的应用203.1 无线信道的特性203.2 CDMA2000系统223.3 CDMA2000的空中接口233.4 CDMA2000物理信道253.5 CDMA2000中Turbo码的关键技术283.6 Turbo码与其他技术的结合303.7 CDMA2000中的Turbo编码器与交织器333.8 小结38第四章Turbo码的Matlab仿真及其仿真结果分析404.1 编码约束度对Turbo码性能的影响404.2 迭代次数对Turbo码性能的影响414.3 交织长度对Turbo码性能的影响424.4 码率对Turbo码性能的影响43结论46致谢48参考文献50第一章绪论1.1第三代移动通信（0001）第三代移动通信系统[1]，简称3G（3rd-generation），是指工作在2G频段上支持高速数据传输的蜂窝移动通讯系统。

纠错编码在通信中的应用研究绪论纠错编码是一种重要的数据通信技术，在数字通信和计算机网络中得到了广泛应用。

其主要功能是通过在数据中添加冗余信息，从而实现在数据传输过程中能够检测和纠正误差的能力。

本文将就纠错编码的原理、种类和应用进行详细介绍，希望更好地掌握该技术在通信中的应用研究。

一、纠错编码的原理纠错编码是通过将数据与纠错码进行组合，以实现检测和纠正数据在传输中出现的误差。

在传输数据的过程中，由于种种原因（例如噪声、失真等），数据很容易发生误差，而纠错编码能够在保证数据传输速率的前提下，提高数据传输的可靠性。

常见的纠错编码包括海明码（Hamming Code）、里德-所罗门码（Reed-Solomon Code）等。

海明码是最早被提出的一种纠错编码，其基本原理是在数据中添加一定数量的冗余位，以检测和纠正数据中的单个比特错误。

里德-所罗门码则在实现海明码的基础上，能够支持检测和纠正更多的比特错误，因而在数据传输可靠性要求较高的场合得到广泛应用。

二、纠错编码的种类1. 海明码海明码由理查德·海明于1950年提出，是最早被用于纠错编码的一种码。

海明码一般采用转换矩阵的形式来表示，其主要功能是检测和纠正单个比特错误。

海明码利用一个生成矩阵将信息位和校验位组合起来，生成的编码可以被接收端进行读取和纠正。

海明码可以在数据传输中检测到传输中发生的单个比特错误，并通过校验位修复受损数据，从而提高数据传输的可靠性和安全性。

2. 里德-所罗门码里德-所罗门码是一种广泛应用于数字通信中的纠错编码。

在信息传输中，里德-所罗门码能够检测和纠正多个比特错误，因而在数据传输可靠性要求较高的场合得到广泛应用。

里德-所罗门码利用了同余和有限域运算的基本知识，以实现检测和纠正多个比特错误。

里德-所罗门码的特点是能够纠正一定数量的错误，因此其应用场合较为广泛，包括数据压缩、数字音频和视频、数字电视、卫星通讯、光纤通讯等等。