核衰变统计规律的验证

实验二 核衰变的统计规律实验人：*** 合作者：*** 实验时间：2011/06/03一、引言对核衰变产生的射线可用计数方式测量。

然而多次测量相同时间间隔内的计数，即使保持相同的实验条件，每次测量的结果并不相同，而是围绕某一平均值上下涨落，反映出核衰变的随机性二、实验目的1、了解并验证原子核衰变及放射性计数的统计性2、了解统计误差的意义，掌握计算统计误差的方法3、学习检验测量数据的分布类型的方法三．原理1．放射性测量的随机性和统计性在做重复的放射性测量中，即使保持完全相同的实验条件（例如放射性的半衰期足够长，因此在实验时间内可以认为其强度基本上没有变化；源与计数器的相对位置始终保持不变；每次测量时间不变；测量仪器足够精确，不会产生其它的附加误差等等），每次的测量结果并不完全相同，而是围绕其平均值上下涨落，有时甚至有很大的差别，也就是说物理实验的测量结果具有偶然性，或者说随机性。

物理测量的随机性产生原因不仅在于测量时的偶然误差，而且更是物理现象(当然包括放射性核衰变)本身的随机性质，即——物理量的实际数值时刻围绕着平均值发生微小起伏。

在微观现象领域，特别是在高能物理实验中，物理现象本身的统计性更为突出。

按照量子力学的原理，对处于同一个态的微观粒子，测量同一个可观测的物理量时，即使不存在任何测量误差，各次测量结果也会不同，除非粒子处于这个可观测量的本征态；比如同一种粒子的寿命，其实测值分布在从相当短到相当长的范围内。

另一方面，所谓偶然的东西，是一种有必然性隐藏在里面的形式；我们正是要通过研究其统计分布规律从而找出在随机数据中包含的规律性。

2．核衰变数的统计分布放射性原子核衰变数的统计分布可以根据数理统计分布的理论来推导。

放射性原子核衰变的过程是一个相互独立彼此无关的过程，即每一个原子核的衰变是完全独立的，与其他原子核是否衰变无关；因此放射性原子核衰变的测量计数可以看成是一种伯努里试验问题。

在N 0个原子核的体系中，单位时间内对于每个原子核来说只有两种可能：A 类是原子核发生衰变，B 类是没有发生核衰变。

G-M特性及核衰变统计规律实验目的1.了解G-M计数器的工作原理，有关特性及使用方法。

2.以G-M计数器为探测设备，验证核衰变的统计规律。

3.了解统计误差的意义，掌握计算统计误差的方法。

实验内容1.在一定甄别阈值下，测量G-M计数管的坪曲线，确定坪曲线的各个参量，并确定其工作电压。

2.用示波器测定计数装置的分辨时间。

3.观察G-M计数管的工作电压与输出脉冲幅度的关系。

4.在相同条件下，对某放射源进行重复测量，画出放射性计数的频率直方图，并与理论正态分布曲线作比较。

5.在相同条件下，对本底进行重复测量，画出本底计数的频率分布图，并与理论泊松分布作比较。

实验原理1G-M计数管1.1G-M管的结构和工作原理G-M计数管是一种气体探测器，结构类型很多，最常见的有圆柱形和钟罩形两种，它们都是由同轴圆柱形电极构成。

图1是其结构示意图，中心的金属丝为阳极，管内壁圆筒状的金属套（或一层金属粉末）为阴极，管内充有一定量的混合气体（通常为惰性气体及少量的猝灭气体），钟罩形的入射窗在管底部，一般用薄的云母片做成；圆柱形的入射窗就是玻璃管壁。

测量时，根据射线的性质和测量环境来确定选择哪种类型的管子。

对于α和β等穿透力弱的射线，用薄窗的管子来探测；对于穿透力较强的γ射线，一般可用圆柱型计数管。

G-M 管工作时，阳极上的直流高压由高压电源供给，于是在计数管内形成一个柱状对称电场。

带电粒子进入计数管，与管内气体分子发生碰撞，使气体分子电离即初电离（γ粒子不能直接使气体分子电离，但它在阴极上打出的光电子可使气体分子发生电离）。

初电离产生的电子在电场的加速下向阳极运动，同时获得能量，当能量增加到一定值时，又可使气体分子电离产生新的离子对，这些新离子对中的电子又在电场中被加速再次发生电离碰撞而产生更多的离子对。

由于阳极附近很小区域内电场最强，则此区间内发生电离碰撞几率最大，从而倍增出大量的电子和正离子，这个现象称为雪崩。

雪崩产生的大量电子很快被阳极收集，而正离子由于质量大、运动速度慢，便在阳极周围形成一层“正离子鞘”，阳极附近的电场随着正离子鞘的形成而逐渐减弱，使雪崩放电停止。

核衰变的指数规律在我们生活的这个世界里，存在着许多神奇而又神秘的现象，核衰变就是其中之一。

核衰变，这个听起来有些高深莫测的名词，实际上与我们的生活息息相关。

而核衰变所遵循的指数规律，更是为我们揭示了原子核内部的奇妙变化。

要理解核衰变的指数规律，首先得知道什么是核衰变。

简单来说，核衰变就是原子核自发地放出粒子或射线，从而转变为另一种原子核的过程。

在这个过程中，原子核的质子数和中子数会发生改变，导致其化学性质和物理性质也发生相应的变化。

那么，为什么核衰变会遵循指数规律呢？这得从原子核的内部结构说起。

原子核是由质子和中子组成的，它们之间存在着强大的相互作用力。

然而，这种相互作用力并不是绝对稳定的，在一定条件下，原子核会处于一种不稳定的状态，从而有自发衰变的倾向。

想象一下，在一个装有许多小球的盒子里，每个小球都代表着一个原子核。

这些原子核都有可能发生衰变。

在某一时刻，一部分原子核衰变了，而剩下的原子核在接下来的时间里，发生衰变的概率并不会受到已经衰变的原子核的影响。

这就好比抛硬币，每次抛硬币得到正面或反面的概率都是独立的，不会因为之前抛的结果而改变。

核衰变的指数规律可以用一个数学公式来表示：N ＝ N₀ × e^（λt) 。

在这个公式中，N 表示经过时间 t 后尚未衰变的原子核数目，N₀表示初始时刻的原子核数目，λ 则被称为衰变常数。

这个衰变常数λ是一个非常重要的参数，它反映了原子核衰变的快慢程度。

λ 的值越大，原子核衰变的速度就越快，反之则越慢。

不同的原子核具有不同的衰变常数，这也就决定了它们衰变的速度和半衰期的长短。

半衰期，这是一个在核衰变中经常提到的概念。

它指的是放射性原子核数目衰变掉一半所需要的时间。

比如说，某种放射性物质的半衰期是 10 天，那么经过 10 天后，原来的放射性物质就只剩下一半了。

再过 10 天，剩下的一半又会衰变掉一半，也就是只剩下四分之一了。

核衰变的指数规律在许多领域都有着重要的应用。

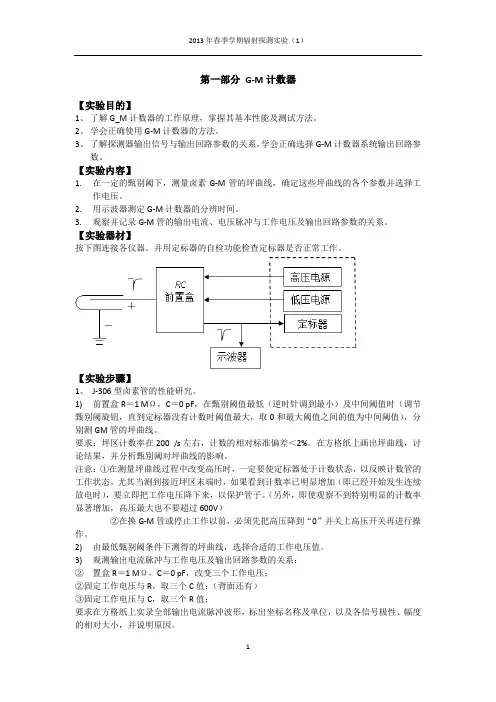
第一部分G-M计数器【实验目的】1、了解G_M计数器的工作原理，掌握其基本性能及测试方法。

2、学会正确使用G-M计数器的方法。

3、了解探测器输出信号与输出回路参数的关系，学会正确选择G-M计数器系统输出回路参数。

【实验内容】1.在一定的甄别阈下，测量卤素G-M管的坪曲线，确定这些坪曲线的各个参数并选择工作电压。

2.用示波器测定G-M计数器的分辨时间。

3.观察并记录G-M管的输出电流、电压脉冲与工作电压及输出回路参数的关系。

【实验器材】按下图连接各仪器。

并用定标器的自检功能检查定标器是否正常工作。

【实验步骤】1、J-306型卤素管的性能研究。

1) 前置盒R＝1 MΩ，C＝0 pF，在甄别阈值最低（逆时针调到最小）及中间阈值时（调节甄别阈旋钮，直到定标器没有计数时阈值最大，取0和最大阈值之间的值为中间阈值），分别测GM管的坪曲线。

要求：坪区计数率在200 /s左右，计数的相对标准偏差＜2%。

在方格纸上画出坪曲线，讨论结果，并分析甄别阈对坪曲线的影响。

注意：①在测量坪曲线过程中改变高压时，一定要使定标器处于计数状态，以反映计数管的工作状态。

尤其当测到接近坪区末端时，如果看到计数率已明显增加（即已经开始发生连续放电时），要立即把工作电压降下来，以保护管子。

（另外，即使观察不到特别明显的计数率显著增加，高压最大也不要超过600V）②在换G-M管或停止工作以前，必须先把高压降到“0”并关上高压开关再进行操作。

2) 由最低甄别阈条件下测得的坪曲线，选择合适的工作电压值。

3) 观测输出电流脉冲与工作电压及输出回路参数的关系：②置盒R＝1 MΩ，C＝0 pF，改变三个工作电压；②固定工作电压与R，取三个C值；（背面还有）③固定工作电压与C，取三个R值；要求在方格纸上实录全部输出电流脉冲波形，标出坐标名称及单位，以及各信号极性、幅度的相对大小，并说明原因。

注意：①中的三个电压值必须在坪区范围内；为观察到形状较好的电流和电压波形，②、③及以下各步骤中的工作电压可比步骤(2)中选择的工作电压低，具体数值可以取R ＝1 M Ω，C ＝0 pF 时，示波器观察电流或电压波形不出现饱和的最大工作电压值。

核衰变的统计规律实验薛佳柳083822一、实验目的1．了解并验证原子核衰变及放射性计数的统计性。

2．了解统计误差的意义，掌握计算统计误差的方法。

3.学习检验测量数据的分布类型的方法。

二、实验原理1. 测量NaI(Tl)闪烁晶体探测器的计数率随工作变化的坪曲线，选定合适的工作电压。

2. 在相同条件下，对某放射源进行重复测量，画出放射性计数的频率直方图并与理论分布曲线作比较。

3. 在相同条件下对本底进行重复测量，画出本底计数的频率分布图，并与理论分布曲线作比较。

4. 用2检验法检验放射性计数的统计分布类型。

三、实验仪器①NaI(Tl)闪烁探测器；②γ放射源（137Cs或60Co)；③高压电源、放大器和多道脉冲幅度分析器。

二、实验内容1．放射性测量的随机性和统计性在做重复的放射性测量中，即使保持完全相同的实验条件（例如放射性的半衰期足够长，因此在实验时间内可以认为其强度基本上没有变化；源与计数器的相对位置始终保持不变；每次测量时间不变；测量仪器足够精确，不会产生其它的附加误差等等），每次的测量结果并不完全相同，而是围绕其平均值上下涨落，有时甚至有很大的差别，也就是说物理实验的测量结果具有偶然性，或者说随机性。

物理测量的随机性产生原因不仅在于测量时的偶然误差，而且更是物理现象(当然包括放射性核衰变)本身的随机性质，即——物理量的实际数值时刻围绕着平均值发生微小起伏。

在微观现象领域，特别是在高能物理实验中，物理现象本身的统计性更为突出。

按照量子力学的原理，对处于同一个态的微观粒子，测量同一个可观测的物理量时，即使不存在任何测量误差，各次测量结果也会不同，除非粒子处于这个可观测量的本征态；比如同一种粒子的寿命，其实测值分布在从相当短到相当长的范围内。

另一方面，所谓偶然的东西，是一种有必然性隐藏在里面的形式；我们正是要通过研究其统计分布规律从而找出在随机数据中包含的规律性。

2．核衰变数的统计分布放射性原子核衰变数的统计分布可以根据数理统计分布的理论来推导。

实验一核衰变与放射性计数的统计规律第一部分 G-M计数器一.实验目的1、了解G-M管的工作原理，掌握其基本性能及其测试方法。

2、学会正确使用G-M管计数装置的方法。

3、了解探测器输出信号与输出回路参数的关系，学会正确选择G-M管计数系统输出回路参量。

二.实验内容1、在一定的甄别阈下，测量卤素G-M管的坪曲线，确定这些坪曲线的各个参量并选择工作电压。

2、用示波器观察法和双源法测定卤素G-M管计数装置的分辨时间。

3、观察并记录G-M计数管的输出电流、电压脉冲与工作电压及输出回路参数的关系。

三.实验原理1、G-M管是一种气体探测器。

当带电粒子射入其灵敏体积时，引起气体原子电离。

电离产生的电子在阳极丝附近的强电场中又引起一系列碰撞电离，即触发“自持放电”。

这一过程产生的电子和正离子向两极漂移时，在外回路产生脉冲信号。

2、从G-M管的工作机制可以看出，入射带电粒子仅仅起一个触发放电的作用，G-M管的输出电流、电压信号的幅度与形状和入射粒子种类与能量无关，只和计数管的几何参量、工作电压以及输出回路参量有关。

在G-M管的使用中，坪特性是其最重要的性能之一。

坪特性是判断管子好坏的主要依据，也是选择管子工作电压的依据。

坪特性曲线就是在一定的实验条件下当入射粒子的注量率不变时，计数管的计数率随工作电压变化的曲线，见图1－1。

图1-1 G-M计数管的坪曲线表征坪特性的参量主要有：起始电压(Vs)：即计数管开始计数时的电压。

坪长： B A =V -V 坪长（单位：百伏） （1-1） 这是管子的工作区域，工作电压一般可选在坪区的21~31的范围内。

坪斜：()100% ()2B A B A B A n n n n V V -=⨯+-坪斜（单位：％/百伏） （1-2） 坪斜主要是由假计数引起的，当然它的值越小越好。

当工作电压高于B V 时，曲线急剧上升，表明管子内发生了持续放电，这会大大缩短管子的寿命，因此在使用中必须注意避免这种情况。

分辨时间的测量
假设测得计数率m，分辨时间为τ，则单位时间内有mτ 时间要产生漏记。若实际的计数率为n，则单位时间内的 漏记数为nmτ
n-m=nmτ
修正后的计数率公式 ：n=m/(1-mτ)
双源法测量分辨时间
• nA=mA/(1-ma τ) • nB=mB/(1-mB τ) • Nab=nA+nB=mAB/(1-mAB τ) • τ =(mA+mB-mAB)/2mAmB
fj :每个分组区间中实际观测到的次数 fj’:每个分组区间中按理论分布应有的出现次数
• 算出随机变数x2所取的值大于某个预定值x21- α的概率P(x2>x21- α), 令此概率为α
• 在检验时，先设定一个小概率α,称为显著性水平，一般设为0.10，可 从表中找到对应的x21- α
• 自由度v=r-s-1 • 若x2<x21- α，则小概率事件未发生，认为此组数据服从泊松分布
核衰变的统计规律
在t时间内平均衰变的原子核的数目：m=N(1-e-λt)
每个核在t时间内发生衰变的几率为1-e-λt，不发生衰变 的几率为e-λt
在t时间内，在N个原子核中有n个核发生衰变的几率为
p(n)=CNn(1-e-λt)n(e-λt)N-n
当N很大且λt<<1时，二项式分布简化为泊松分布
射粒子的数目
所产生的负离子在电场 加速下向阳极运动
负离子与气体分子发生 碰撞打出更多的次级电
子，引起了“雪崩放 电”，在阳极上便得到
一个负的电压脉冲
为了使一个辐射粒子 引起放电后只计一次 数，在计数管内加入 少量猝灭的气体，用 来猝灭正离子鞘和电 离产生的离子增殖。
电流I与计数率的关系
图（1）

实验验证的最新成果和发现
实验方法：使用高能 粒子加速器进行实验
最新成果：发现了新 的放射性衰变模式
发现意义：为理解原 子核结构和放射性衰 变提供了新的视角
未来展望：预计未来会 有更多新的实验方法和 发现，进一步推动原子 核结构和放射性衰变研 究的发展。
实验验证的未来展望和发展方向
实验技术的进 步：如加速器、 探测器等技术 的改进，提高 实验精度和效 率
实验方法：使用电子散射 实验和质子散射实验
实验目的：研究原子核的 结构和性质
实验结果：证实了原子核 的存在和性质
实验意义：为原子核物理 的发展奠定了基础
放射性衰变的实验观测
放射性衰变实验：通过测量放射性元素的衰变率来验证放射性衰变理论
实验方法：使用放射性元素探测器，如盖革计数器，测量放射性元素的衰变率
放射性衰变的实验验证
放射性衰变的类型和特点
α衰变：释放氦 核，能量高，穿
透力强
β衰变：释放电 子或正电子，能 量较低，穿透力
较弱
γ衰变：释放高 能光子，能量最 高，穿透力最强
特点：放射性衰 变是原子核自发 的过程，遵循能 量守恒和动量守 恒定律，释放的 能量和粒子的种 类与原子核的组 成和结构有关。
提高实验技术：实验验证可以提高实验技术，为未来的实验研究奠定基础。
促进国际合作：实验验证可以促进国际合作，共同解决全球性问题。
03
原子核结构的实验验证
原子核的组成和结构
质子和中子通过强相互作 用力结合在一起
原子核由质子和中子组成
原子核的形状和结构可以 通过散射实验来研究
原子核的稳定性可以通过 核裂变和核聚变来验证
观测仪器：使用辐射探测器、闪烁探测器等仪器进行测量 数据分析：通过数据分析，验证放射性衰变的规律和理论模型

实验10-2 核衰变的统计规律【实验目的】1．测量NaI(Tl)闪烁探测器的坪曲线，确定合适的工作电压；指导：用闪烁探测器测量强度不变的放射源时，改变光电倍增管的高压，计数率也会随之改变；原因在于任何一种射线在闪烁探测器中产生的脉冲幅度都不会完全一样，输出脉冲的幅度也分布在一定范围内。

尽管如此，只要射线的能量不是特别低而探测器的工作状态又选择得当，绝大部分信号脉冲都会比光电倍增管的噪声脉冲大。

当电压足够高，信号脉冲幅度基本上都超过了仪器的甄别阈而绝大部分噪声的幅度又还比甄别阈小很多时，随着高压的增加计数率的增加就很缓慢了，这时就出现了“坪区”。

在实验中，重要的是向学生说明在许多核物理实验中测量坪曲线的意义何在。

在本实验中，由于高压相对比较稳定，因此我们在实践中发现选取坪曲线较为平坦（计数率随高压漂移变化较小）的工作点和坪曲线较为陡峭的工作点两者的差异不大。

2．了解并验证原子核衰变及放射性计数的统计性；指导：本实验通过反复测量放射源（137Cs 或60Co ）在一段时间内强度并作为一个随机事件，取一个样本容量为A 的样本来观察其结果是否符合正态分布。

当然，源的强度本身随时间衰减，但137Cs 的半衰期长达30年，可以近似认为在实验时间内（大约1——2小时）源强不变。

3．了解统计误差的意义，掌握计算统计误差的方法；指导：这一实验需要一定的概率论和数理统计方面的基础，比如二项式分布、泊松分布、正态分布以及样本均值、样本方差、样本方差的无偏估计；学生应该已经学习过相关课程，若没有接受过类似训练，实验讲义的原理部分已经列出了所需知识。

需要说明的是： 鉴于A x x Ai i /)(12∑=-不是方差2S 的无偏估计，)1/()(12--∑=A x x Ai i 才是，因此取)1/()(12--=∑=A x x S Ai ix 作为样本标准差的无偏估计。

（参见任一概率论数理统计教材） 4．学习检验测量数据的分布类型的方法。

盖革-弥勒计数器及核衰变的统计规律盖革-弥勒计数器是气体探测器的一种，用来测定射线强度，既单位时间的粒子个数。

近年来，随着闪烁探测器及半导体探测器的发展，其重要性有所下降，但由于它的设备简单，使用方便，在有关的放射性测量中仍在广泛使用。

一、实验目的掌握G-M计数器的工作基础，测定其有关特性，学会使用；以G-M计数器未测试设备，验证核衰变的统计规律；学会使用放射性测量结果的误差表示法，学会多次测量结果的误差计算及测试时间的选择。

二、实验原理1、G-M计数器原理：G-M计数器是利用射线使计数管内的工作气体电离，然后收集产生的电荷来记录射线的探测器。

玻璃管内有圆筒状阴极，在阴极对称轴上装有丝状阳极。

先将管内抽成真空，再充入一定量的惰性气体和少量猝灭气体（卤素或有机物）在G-M计数管两级加上电压，设其阳极半径为a，阴极半径为b，阳极与阴极间的电压为U，则沿着管径向位置为r处的电场强度为，可见随着r减小，电场强度增大，且阳极附近急剧增大。

2、脉冲原理（1）当射线进入G-M管中使得管中气体电离后，正离子和负离子在管内电场的作用下分别向阴极和阳极移动。

在阳极附近强大的电场作用下，电子获得强大的动能以至于将阳极附近的气体电离。

经过多次碰撞，殃及附近的电子急剧增多，形成了“雪崩电子”；在这些碰撞中会产生大量的紫外线光子，这些光子能进一步的产生第二波的“雪崩”效应，增加电子。

这个电子不断增加的过程称为气体放大。

（2）雪崩过程发生在殃及附近，加上电子的质量远远小于阳离子的质量，速度比阳离子快，因此电子很快被阳极吸收，在管内留下一个被大量阳离子构成的阳离子鞘包围着的阳极。

正离子鞘将随着电离的发生逐渐增厚，由于正离子鞘的作用，阳极附近的电场将随之减小，以致新电子无法增殖，即电场强度不足以引发雪崩效应，雪崩效应停止，正离子鞘停止生成，放电便终止了，伺候，正离子鞘在电场的作用下慢慢移向阴极，最后到达阴极被中和，阳极附近的电场也随之恢复，使得与G-M串联的电阻记录下一个电压脉冲。

dN dt
(P
B)N
e
N
eff
Bio
Phys
式中λe 为有效衰变常数，λP 是物
理衰变常数，λB 为生物衰变常数。
依据半衰期与衰变常数的关系，有：
或：
11 1
Teff
T T Bio
Phys
Te
TP TB TP TB
五、放射性活度
放射性活度 A (radioactivity)
半衰期 —— 放射性核素减 少一半所需要 的时间。
T1 2
ln 2
T1 2
0.693
N0 2
N e T1 2 0
T1 2
ln 2
0.693
λ↑→ T↓→ 核素衰变得愈快。
自然界中各种放射性核素的半衰期长 短不一，长的可达数十亿年，短的不
足 1 s。
annual 每年的
半衰期的单位为：年(a)、天(d)、小
时(h)、分(min)和秒(s)等。
在一种放射物中，有些原子核衰变得 早些，有些则衰变得晚些，
就是说有的寿命短，有的寿命长。可 以用数学来求出平均寿命值。
τ平均寿命(mean life) —— 设原
来未衰变的原子核数为 N，在 t ～ ( t + dt ) 的时间间隔内，
在 t ～ (t + dt) 的时间间隔内， 核衰变的数目为： - dN = λNdt ，
—— 用单位时间内衰变掉的原子核 数来衡量放射源的放射性强弱。
A dN N
dt
即：放射源在单位时间内发出的射 线愈多，其衰变的核素也愈多。
A N0 exp( t) A0 exp( t)
或：A
(N0 ) et
A et 0

盖革-米勒计数器及核衰变统计规律方啸（南开大学物理科学学院，天津 300071）【摘要】本文介绍了盖革-米勒计数器的基本结构、工作原理和性能，并给出了核衰变的理论统计规律。

之后作者通过设计实验和分析数据测量了盖革-米勒计数管的坪特性，并验证了核衰变的统计规律。

【关键字】盖革-米勒计数器计数管坪特性核衰变统计规律1.引言盖革-米勒计数器（G-M计数器）是一种气体电离探测器，由德国物理学家盖革（Hans Wilhelm Geiger,1882～1945）和米勒（E. Walther Muller，1905～1979）在1928年发明[1]。

G-M计数器与正比计数器类似，但所加的电压更高。

带电粒子射入气体，在离子增殖过程中，受激原子退激，发射紫外光子，这些光子射到阴极上产生光电子，光电子向阳极漂移，又引起离子增殖，于是在管中形成自激放电。

为了使之能够计数，计数器中充有有机气体或卤素蒸气，能吸收光子，起到猝灭作用。

盖革-米勒计数器优点是灵敏度高，脉冲幅度大，缺点是不能快速计数。

1908年，盖革按照卢瑟福（ E. Ernest Rutherford，1871～1937）的要求，设计制成了一台α粒子计数器。

卢瑟福和盖革利用这一计数器对α粒子进行了探测。

从1920年起，盖革和米勒对计数器作了许多改进，灵敏度得到很大提高，被称为盖革-米勒计数器，应用十分广泛。

本文第二个部分先介绍了G-M计数器的结构组成，阐述了其重要部件G-M 计数管的工作原理和性能。

第三部分给出了核衰变的理论统计规律，并对测量误差做出了理论估计。

第四部分是实验的具体设计。

第五部分对实验获得的数据进行分析处理。

实验成功测得了G-M计数管的坪特性，并验证了核衰变的统计规律。

2.G-M计数器图1 G-M计数器实验装置图G-M计数器由G-M计数管、高压电源和定标器三部分组成（如图1）。

G-M计数管按用途可分为γ计数管(常见圆管型）和β计数管(常见钟罩型)(如图2)。

衰变统计规律衰变统计规律：在放射性衰变过程中，对于某个特定的放射性核素，其衰变的发生是完全随机且不可预测的，但从大量的原子核来看，其衰变又呈现出一定的统计规律，即在某一固定时间段内，发生衰变的原子核数目是相对稳定的。

嘿，想象一下，这些放射性原子核就像是一群调皮的小精灵，它们可不会乖乖地按照我们期望的方式行动。

它们什么时候衰变，那完全是看它们自己的心情，没有任何规律可循，特别任性！但神奇的是，当把它们聚在一起形成一个庞大的群体时，它们的行为又好像被一只无形的大手给规范住了。

就好像这些小精灵在玩一个特别的游戏，每个小精灵都有可能随时“出局”，也就是发生衰变。

单个小精灵的行为是完全无法预料的，它可能下一秒就“出局”了，也可能等了好久都不“出局”。

但是呢，如果有一大群这样的小精灵，我们就会发现，在一段时间内，总会有差不多固定数量的小精灵“出局”。

这就好像它们虽然各自为战，但冥冥之中又遵循着某种神秘的规则。

比如说铀这种放射性元素吧，它的原子核就一直在玩着这个衰变的游戏。

在一大块铀矿石中，每时每刻都有铀原子核在发生衰变，但我们无法确切地知道下一个衰变的会是哪一个。

然而，通过长时间的观察和统计，我们可以大致算出在一定时间内会有多少铀原子核发生衰变。

这就像是我们虽然不知道彩票的中奖号码是多少，但我们可以通过统计数据大致了解到中奖的概率有多大。

而且啊，这种衰变统计规律在很多领域都有着重要的应用呢。

在核物理学中，科学家们通过研究这种规律来深入了解原子核的结构和性质；在医学上，利用放射性同位素的衰变规律可以进行疾病的诊断和治疗，比如放射性治疗癌症，就是根据衰变规律来精确控制辐射剂量的。

总之，衰变统计规律虽然听起来很神秘，但它却在我们的生活和科学研究中发挥着重要的作用。

它让我们对这个世界的认识更加深入，也为我们解决各种问题提供了有力的工具。

如果你对这些神奇的科学规律感兴趣，不妨去看看相关的科普书籍，或者上网搜索一些专业的科学网站，那里有更多有趣的知识等待着你去探索。

实验四 核衰变的统计规律与放射性测定的实验数据处理学生： 学号：同组：一、实验目的1. 验证核衰变所服从的统计规律2. 熟悉放射性测量误差的表示方法3. 了解测量时间对准确度的影响4. 学会根据准确度的要求选择测量时间 二 、实验原理实验证明,在对长寿命放射性物质活度进行多次重复测量时，即使周围条件相同，每次测量的结果仍不相同。

然而，每次结果都围绕某一平均值上下涨落，并且，这种涨落是服从一定的统计规律的。

假如在时间间隔t 内核衰变的平均数为n ，则在某一特定的时间间隔t 内，核衰变为n 的出现机率P(n)服从统计规律的泊松分布：()()!n nn P n e n -= （2-4-1） 图一表示n =3.5的泊松分布曲线。

泊松分布在平均数n 较小的情况下比较适用；如果值相当大，计算起来十分复杂，实际应用对泊松分布利用斯蒂令近似公式： !2n n n n n e π-≈⋅⋅ （2-4-2） 化为高斯分布，得：2()21()2n n nP n enπ--= （2-4-3）高斯分布说明，与平均值的偏差()n n -对于n 而言具有对称性，而绝对值大的偏差出现的几率小。

放射性衰变并不是均匀地进行，所以在相同的时间间隔内作重复的测量时测量的放射性粒子数并不严格保持一致，而是在某平均值附近起伏。

通常把平均值n 看作是测量结果的几率值，并用它来表示放射性活度，而把起伏带来的误差叫做测量的统计误差，习惯用标准误差n ±来表描述。

实验室都将一次测量的结果当作平均值，并作类似的处理而计为N N ±。

图 1泊松分布曲线图 2 高斯分布曲线计数的相对标准误差为：= （2-4-4）它能说明测量的准确度。

当N 大时，相对标准误差小，而准确度高。

反之，则相对标准误差大，而准确度低。

为了得到足够计数N 来保证准确度，就需要延长测量时间t 或增加相同测量的次数m 。

根据计算可知，从时间t 内测的结果中算出的计数率的标准误差为：t ±== （2-4-5） 计数率的相对标准误差E 用下式表示：E == （2-4-6）若实验重复进行m 次，则平均计数率的标准误差等于：（2-4-7） 考虑本底后，标准误差为：σ== （2-4-8） N c 为t c 时间内源加本底的计数，n b 为t b 时间内本底的计数，n c 为源加本底的计数率，n b 为本底的计数率。

P(x)
1
( x )2
e 2 2
2
两种分布
两种检验法
χ2检验法
2 r ( f j kp j )2
j 1
kp j
j为分组数，fj为各组实际频数，pj为各组理论概率，k为
总频数 。其近似地服从χ2分布 。
统计量χ2可用来衡量实测分布与理论分布之间有无明显
的差异。
《热力学·统计物理》第三版 汪志成 高等教 育出版社
谢谢!
χ2分布的图形
两种检验法
频率直方图检验法
作频率直方图。将所得到的频率直方图与理论分布曲线相 比较，来定性判断测量数据分布是否合理。
实验装置
实验结果及分析
低计数（泊松分布）
第一次测量：Cs源，时间间隔0.1s，测量300个样本点
概率
0.25
0.2 0.15
0.1 0.05
0 0 1 2 3 4 5 6 7 8 9 10 11 记录个数分类
χ2检验法
组数r=11，泊松分布s=1=>自由度v=9 取显著性水平α=0.1，查表得χ1- α2=14.684
χ2<χ1- α2成立！
服从泊松分布
再试两次：
平均值=3.367，组数r=11，χ2=8.351 平均值=3.384，组数r=11，χ2=11.473
的确发生 了小概率 事件！
实验结果及分析
如果出现χ2>χ1- α2的情况，也不可断然认定 核衰变不符合理论分布，而要进一步详细 分析原因。一般来说可以多测几组数据， 再做具体分析，记住小概率事件也是可能 发生的
参考书目
《近代物理实验补充讲义》 复旦大学物理教学 实验中心

0.05
3.841 5.991 7.815 11.07 14.07 16.92 18.31 25.0 31.41 37.65 43.77
布.
2. 实验与分析
装置简图
统计规律的验证
1. 低计数(泊松分布):分别用Tl 和Cs,控制时间,使计数平均值在3~5 之间,取
300 个样本.
下表中左边数据是Tl,右边是Cs
和χ 2 1−α
,若χ2<
χ2 1−α
,就认为数据服从泊松分
χ2 1−α
v
1
2
3
5
7
9
10
15
20
25
30
α
0.50
0.455 1.165 2.366 4.351 6.346 8.343 9.342 14.34 19.34 24.34 29.34
0.10
2.71 4.61 6.25 9.24 12.0 14.684 16.0 22.3 28.4 34.4 40.3
图的形状
从图中可以看出随机变数χ2
所取的值大于某预定值χ12−α
的概率
p(χ2>
χ2 1−α
),令此概
率为α 则
∫ p(χ2>
χ2 1−α
)=
∞ p(χ 2 )d χ 2 = α
χ12−α
实验时要求总次数不少于50.比较时先取一个小概率α (本实验取0.1),称为显著
性水平,查表得χ12−α
的值,比较统计量χ2
9
4/5
0.0133/0.0166
0.0162/0.0152
10
1/3
0.0033/0.0099
0.0067/0.0062

1放射性衰变涨落的统计规律实验放射性衰变涨落的统计规律实验⼀、实验⽬的1、证放射性衰变的涨落性2、了解统计误差的意义，掌握计算统计误差的⽅法3、统计检验放射性衰变涨落的概率分布类型4、学会⽤列表法和作图法表⽰实验结果⼆、实验内容1、相同实验条件下，多次重复测量某放射源的计数及测量装置的放射性本底计数2、⽤列表法和作图法表⽰实验结果：列出频数、频率统计表和χ2检验表；作放射源和本底计数的频数、频率和累计频率曲线图3、作χ2检验，确定放射源和本底计数的概率分布类型三、FD3013仪器简介：为便携式，操作⽅便、它适⽤于地质油矿普查、同位素放射源检测。

也使⽤于如核电、医院、实验室及废旧钢材等放射性同位素场合的检测。

1、仪器⼯作原理：γ射线经过外包壳后与探测器NaI（TI）晶体发⽣作⽤产⽣次级电⼦，它使闪烁体分⼦电离和激发，退激时发出⼤量光⼦荧光（其有各向同性，光谱范围从可见光到紫外光），在闪烁体周围包以反射物质，这样能使光⼦集中向光电倍增管（由光阴极和若⼲个打拿极和⼀个阳极组成）。

闪烁光⼦经光电倍增管，由于光电效应会产⽣光电⼦，这些光电⼦受极间电场加速和聚焦，打在第⼀个打拿极上，产⽣3～6个⼆次电⼦，这些⼆次电⼦在以后的打拿极上发⽣同样的倍增FD3013数字γ辐射仪过程，直到最后在阳极上可接收到104～109个电⼦。

这些电⼦在阳极负载上形成电压脉冲，通过起阻抗匹配作⽤的射极跟随器，传送到电压甄别器进⾏脉冲幅度甄别，当脉冲幅度⾼于甄别阈40kev时会形成⼀个计数信号，触发后续计数电路计数（低于甄别阈40kev的脉冲不会引起计数）。

CPM测量：计数选通cpm计数⽀路（⾯版上转换按钮置于cpm档），进⾏64s的计数测量。

测量结束后，计数选通门关闭，给出8秒显⽰计数。

显⽰结束后进⾏监测。

PPM测量：（⾯版上转换按钮置于ppm档）计数选通ppm计数⽀路，先进⾏1s的判测计数。

当计数在0～99时，⾃动选择16s 档的测量时间；计数在100～199时，⾃动选择4s档的测量时间；计数在200以上时，⾃动选择2s档的测量时间。