衰变规律

放射性元素的半衰期与衰变规律在我们探索物质世界的奥秘时，放射性元素的半衰期与衰变规律是一个引人入胜且至关重要的领域。

这不仅在科学研究中具有重要意义，也在许多实际应用中发挥着关键作用。

首先，让我们来了解一下什么是放射性元素。

简单地说，放射性元素就是那些原子核不稳定，会自发地放出射线（如α射线、β射线、γ射线等），从而转变为另一种原子核的元素。

这种自发的变化过程就被称为衰变。

而半衰期，是描述放射性元素衰变快慢的一个重要概念。

它指的是放射性元素的原子核有半数发生衰变所需的时间。

打个比方，如果一种放射性元素的半衰期是 1 天，那么经过 1 天后，原来的放射性元素就会有一半变成了其他物质。

不同的放射性元素具有不同的半衰期。

有的半衰期非常短，可能只有几微秒甚至更短；而有的则很长，可以达到数十亿年。

比如，碘131 的半衰期约为 8 天，而铀 238 的半衰期则长达约 45 亿年。

放射性元素的衰变规律遵循着一定的数学规律。

假设初始时刻放射性元素的原子核数目为 N₀，经过时间 t 后，剩余的原子核数目为 N，那么它们之间的关系可以用公式 N ＝ N₀ ×（1/2)＾（t/T) 来表示，其中 T 就是该放射性元素的半衰期。

那么，为什么会有半衰期和衰变这种现象呢？这其实与原子核内部的结构和能量状态有关。

原子核由质子和中子组成，它们之间存在着很强的相互作用力。

当原子核的结构不稳定，内部能量过高时，就会通过释放粒子或射线来降低能量，达到更稳定的状态，这就是衰变的本质。

半衰期的长短取决于多个因素。

首先是原子核内部的结构和质子、中子的比例。

如果这个比例不合适，原子核就更容易发生衰变。

其次，原子核的质量也会影响半衰期。

一般来说，质量较大的原子核相对更不稳定，半衰期可能较短。

放射性元素的半衰期和衰变规律在许多领域都有着广泛的应用。

在医学上，放射性同位素常用于诊断和治疗疾病。

例如，碘 131 可以用于治疗甲状腺疾病，因为甲状腺会吸收碘。

放射性衰变放射性核素的衰变规律放射性衰变是一种自然现象，指的是放射性核素在时间上逐渐减少自身的不稳定性。

本文将深入探讨放射性衰变的规律，并解释放射性核素的衰变过程。

一、放射性衰变的概念及特点放射性衰变是指放射性核素发生自发性的衰变现象，通过释放射线和/或粒子来达到更稳定的状态。

放射性衰变具有以下几个特点：1. 随机性：放射性衰变是完全随机的，不受任何外界影响。

2. 自发性：放射性核素在不依赖外界因素的情况下自行发生衰变。

3. 不可逆性：放射性核素一旦发生衰变，就无法逆转。

二、放射性衰变类型及衰变规律放射性衰变可以分为α衰变、β衰变和γ衰变。

下面将逐一对三种衰变类型进行阐述。

1. α衰变α衰变是指放射性核素通过释放氦离子（α粒子）来衰变。

α粒子包括两个质子和两个中子，其电荷为+2。

α衰变的衰变规律符合指数衰减定律，即放射性核素的数量随时间按指数函数减少。

衰变速率与放射性核素的数量成正比，可以用以下公式来计算α衰变的放射性核素数量N：N = N0e^(-λt)其中，N是某一时刻的放射性核素数量，N0是初始放射性核素数量，λ是衰变常数，t是经过的时间。

2. β衰变β衰变是指放射性核素通过释放电子（β粒子）或正电子（β+粒子）来衰变。

β衰变可以进一步分为β-衰变和β+衰变。

β-衰变的衰变规律与α衰变相似，也符合指数衰减定律。

β+衰变则是通过正电子与电子的相遇并湮灭，释放出γ光子。

3. γ衰变γ衰变是指放射性核素通过释放γ光子来衰变。

γ光子是高能量电磁波，具有较强穿透力。

γ衰变的衰变规律较为特殊，不依赖于时间或数量的指数函数。

放射性核素的γ衰变是连续的，直到衰变成一个稳定的核素。

三、半衰期和衰变常数半衰期是指放射性核素衰变至原始数量的一半所需的时间。

每种放射性核素都有其独特的半衰期。

半衰期与放射性核素的衰变常数有关，它们之间的关系可以用以下公式表示：t(1/2) = ln2 / λ其中，t(1/2)是半衰期，λ是衰变常数，而ln2是自然对数的2为底的对数。

半衰期放射性元素的衰变规律放射性元素具有一定的不稳定性，会在一定时间内发生衰变。

衰变是指原子核发生变化，释放出辐射以获得更稳定的状态。

而放射性元素的衰变规律可以通过其半衰期来描述。

本文将详细介绍半衰期放射性元素的衰变规律。

一、放射性元素的定义和特性放射性元素指的是那些原子核不稳定，能够通过自发衰变释放辐射的元素。

这些元素的原子核中的中子和质子的比例不合适，导致核力不平衡，因此它们会发生衰变，转化为更稳定的元素。

放射性元素的特性包括衰变产物的释放、辐射的种类、放射性强度等。

当放射性元素发生衰变时，会释放出α粒子、β粒子或伽马射线。

每种辐射具有不同的能量和穿透能力，因此其对人体和环境的影响也各不相同。

二、半衰期的概念和计算方法半衰期是指放射性元素衰变到其初始数量的一半所需的时间。

它是描述放射性元素衰变速率的重要参数。

半衰期的计算方法可以通过放射性元素的指数衰变方程来推导。

对于放射性元素A而言，其衰变速率dN/dt与剩余原子核数目N成正比，即dN/dt = -λN。

其中，λ为衰变常数。

根据微分方程的求解方法，可以得出放射性元素A的衰变规律公式N = N0 * e^(-λt)。

当衰变时间t等于半衰期T时，剩余原子核数目为初始数目的一半，即N0/2。

代入衰变规律公式可得：N0/2 = N0 * e^(-λT)。

整理后可得到半衰期的计算公式T = ln2 / λ。

三、半衰期放射性元素的应用半衰期放射性元素具有广泛的应用领域。

它们可以用于核能的生产和利用、医学诊疗、地质学研究等方面。

在核能的生产和利用中，半衰期放射性元素可以用于核反应堆的燃料、放射性同位素的制备和处理等方面。

通过控制衰变速率，可以实现能源的高效利用和核材料的安全管理。

在医学诊疗中，半衰期放射性元素常被用作放射治疗和影像学检查的辐射源。

例如，放射性碘被广泛应用于甲状腺疾病的治疗，放射性铯用于治疗深部肿瘤等。

在地质学研究中，半衰期放射性元素可以用于年代测定和岩石、土壤等介质的物质循环研究。

放射性同位素的衰变规律研究在我们生活的这个世界中，存在着许多神秘而又神奇的现象，放射性同位素的衰变就是其中之一。

放射性同位素的衰变并非随机发生，而是遵循着一定的规律，这些规律的发现和研究对于我们理解物质的本质、探索宇宙的奥秘以及在众多领域的应用都具有极其重要的意义。

首先，我们来了解一下什么是放射性同位素。

同位素，简单来说，就是指质子数相同但中子数不同的同一元素的不同原子。

而放射性同位素，则是指那些会自发地放出射线，从而发生衰变的同位素。

这些射线包括α射线、β射线和γ射线等。

放射性同位素的衰变规律可以用一个关键的概念来描述，那就是半衰期。

半衰期指的是放射性同位素的原子核有半数发生衰变所需要的时间。

不同的放射性同位素具有不同的半衰期，有的短至几毫秒，有的则长达数十亿年。

例如，碘-131 的半衰期约为 8 天，而铀-238 的半衰期则长达约 45 亿年。

那么，放射性同位素为什么会发生衰变呢？这要从原子核的内部结构说起。

原子核由质子和中子组成，它们之间存在着强大的相互作用力。

然而，在某些情况下，原子核的内部结构可能不稳定，这种不稳定性导致了原子核自发地发生变化，以达到更稳定的状态，这个过程就是衰变。

在衰变过程中，放射性同位素会按照一定的概率发生衰变。

这种概率是固定不变的，不受外界条件的影响，比如温度、压力、化学环境等。

这是放射性衰变的一个重要特点。

放射性同位素的衰变规律可以用数学公式来表示。

假设初始时刻放射性同位素的原子核数目为 N₀，经过时间 t 后，剩余的原子核数目为N，则它们之间的关系可以用以下公式表示：N ＝ N₀ ×（1/2)＾（t ／T) ，其中 T 为该放射性同位素的半衰期。

通过对这个公式的研究和应用，我们可以预测在一定时间后放射性同位素的剩余量，这在许多领域都有着重要的应用。

在医学领域，放射性同位素的衰变规律被广泛应用于诊断和治疗疾病。

例如，利用碘-131 对甲状腺疾病进行诊断和治疗。

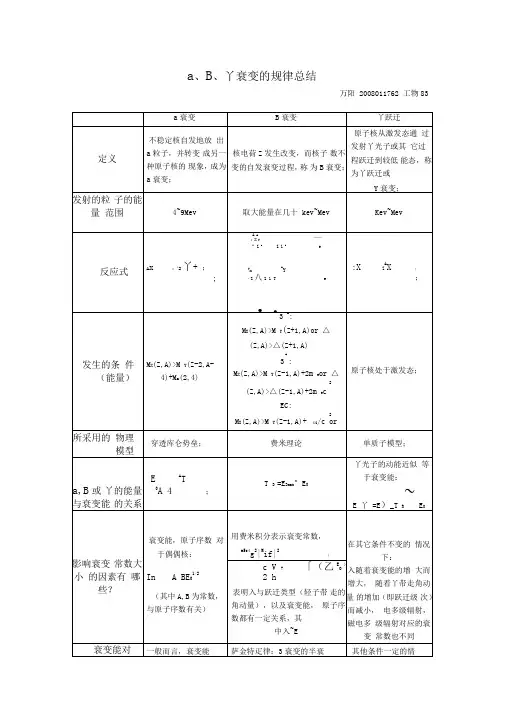
α、β、γ衰变的规律总结万阳 2008011762工物 83α 衰变β 衰变γ 跃迁不稳定核自发地放原子核从激发态通核电荷 Z 发生改变，而核子过发射 γ 光子或其出 α 粒子，并转变定义数不变的自发衰变过程，称它过程跃迁到较低 成另一种原子核的 为 β 衰变；能态，称为 γ跃迁或现象，成为 α 衰变；γ 衰变；发射的粒 子的能量4~9Mev范围反应式ZAXA Z 42Y+ ；发生的条 M X (Z,A)>M Y (Z-2,A- 件（能量） 4)+M α(2,4)所采用的穿透库仑势垒；物理模型α，β或Aγ的能量 E 0与衰变能 TA 4 ；的关系最大能量在几十 kev~Mev Kev~Mev: Z A XZA1Ye，: Z A XZ A 1Ye ，ZAXZAX；EC : Z AX e iZ A1Y e ；β - ：M X (Z,A)>M Y (Z+1,A)or(Z,A)>(Z+1,A)β +：M(Z,A)>M (Z-1,A)+2m or原子核处于激发态；XYe(Z,A)>(Z-1,A)+2m e c 2EC ：XYi/c 2M(Z,A)>M (Z-1,A)+ εor(Z,A)> (Z-1,A)+ ε i ；费米理论单质子模型；γ 光子的动能近似T β =E βmax ≈ E 0等于衰变能：E γ =E 0-T R ≈ E 0衰变能，原子序数用费米积分表示衰变常数，在其它条件不变的情况下：对于偶偶核：m 5e c 4 g 2 M if2λ 随着衰变能的增大而增大，影响衰变1/2常数大小 lnA BE 0的因素有（其中 A ，B 为常哪些？数，与原子序数有关）衰变能对一般而言，衰变能23 7f (Z , E 0 )表明 λ 与跃迁类型（轻子带走的角动量），以及衰变能，原子序数都有一定关系，其中λ ~E 05萨金特定律： β 衰变的半衰随着 γ 带走角动量的增加（即跃迁级次）而减小，电多级辐射， 磁电多级辐射对应的衰变常数也不同其他条件一定的情衰变的影越大， α 粒子穿透响库仑势垒概率越大，衰变常数越大，α 衰变越容易发生；α 衰变过程中角动 角动量对 量守恒，这影响后面的选择定则；同 衰变的影 时 α 粒子带走的角响是怎样 动量越小，衰变越 的？为什容易发生，因为 α么？粒子穿透势垒的离心势会变小。

药物衰变规律药物的半衰期一般指药物在血浆中最高浓度降低一半所需的时间。

例如一个药物的半衰期（一般用t1/2表示）为6小时，那么过了6小时血药物浓度为最高值的一半；再过6小时又减去一半；再过6小时又减去一半，血中浓度仅为最高浓度的1/8。

药物的半衰期反映了药物在体内消除（排泄、生物转化及储存等）的速度，表示了药物在体内的时间与血药浓度间的关系，它是决定给药剂量、次数的主要依据，半衰期长的药物说明它在体内消除慢，给药的间隔时间就长；反之亦然。

消除快的药物，如给药间隔时间太长，血药浓度太低，达不到治疗效果。

消除慢的药物，如用药过于频敏，易在体内蓄积引起中毒。

每一种药物的半衰期各不一样；即使是同一种药物对于不同的个体其半衰期也不完全一样；成人与儿童、老人、孕妇，健康人与病人，药物半衰期也会有所不同。

通常所指的药物半衰期是一个平均数。

肝肾功能不全的病人，药物消除速度慢，半衰期便会相对延长。

如仍按原规定给药，有引起中毒的危险，这点必须特别注意。

根据半衰期的长短给药，可以保证血药浓度维持在最适宜的治疗浓度而又不致引起毒性反应。

常用的适宜方案是首次给以全负荷剂量，然后根据药物半衰期间隔一定时间，再给以首次剂量的一半。

例如磺胺嘧啶1克能在血中产生有效浓度，其半衰期为17小时，因此适宜方案是每日服两次，首剂2克，以后1克一次。

但对一些半衰期过短或过长的药物，如仍按半衰期给药，前者可能给药次数太频；而后者血药浓度波动较大，甚或由于间隔时间太长，易于遗忘给药。

鉴于上述情况，对于毒性不大的药物，如半衰期过短，可以加大首次剂量，使其在间隔时间末段仍保持有效剂量。

倘若药物的治疗指数小，半衰期又短，如去甲肾上腺素，一次注射仅维持几分钟，就必须采用静脉滴注法给药。

倘若某药物的半衰期大大超过24小时，则可采用首次剂量和每天服用维持量的方案。

维持量的大小可以根据该药首次剂量、每天给药量和该药的半衰期运用公式计算而得。