2019年中考数学总复习第四单元图形的初步认识与三角形课时训练22锐角三角函数及其应用练习湘教版

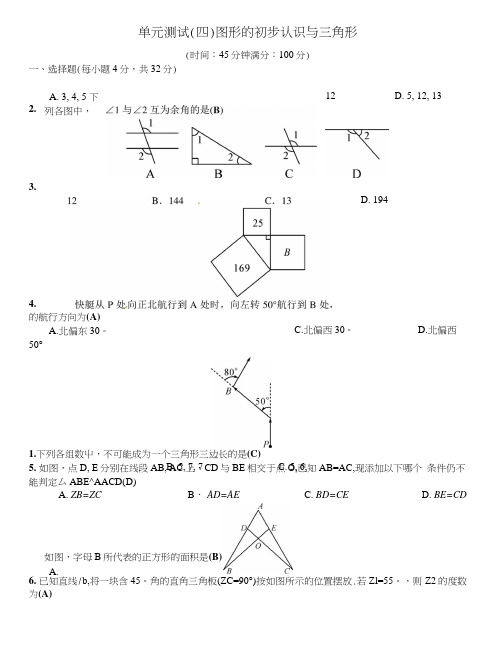
单元测试(四)图形的初步认识与三角形(时间：45分钟满分：100分)一、选择题(每小题4分，共32分)1.下列各组数屮，不可能成为一个三角形三边长的是(C)5. 如图，点D, E 分别在线段AB, AC 上，CD 与BE 相交于点O,已知AB=AC,现添加以下哪个 条件仍不能判定厶ABE^AACD(D)A. ZB=ZC B ・ AD=AE C. BD=CE D. BE=CD 6. 已知直线/b,将一块含45。

角的直角三角板(ZC=90°)按如图所示的位置摆放.若Zl=55。

，则 Z2的度数为(A)2. A. 3, 4, 5 下列各图中， 12 D. 5, 12, 13 3.D. 1944.的航行方向为(A)A.北偏东30。

50° C.北偏西30。

D.北偏西B. 5, 7, 7 如图，字母B 所代表的正方形的面积是(B)A. C. 5, 6,A. 80°B. 70°C. 85°•D. 75°7. 如图，在AABC 中，AC = 8, ZABC = 60。

，ZC=45。

，AD 丄BC,垂足为 D, ZABC 的平分线交 AD 于点E,则AE 的长为(C)8•女U 图，E, F 是口 ABCD 对角线上AC 两点，AE=CF=#AC.连接DE, DF 并延长，分另交AB, BC 于点G, H,连接GH,则的值为(C)'△BGH二、填空题(每小题4分，共24分) 9. 如图，在厶ABC 中，ZACB=90°, CD 〃AB, ZACD=40。

，则ZB 的度数为岂10. 如图所示，小明同学利用一个锐角是30。

的三角板测量一棵树的高度，测量时「如图所示放置三角 板，已知他与树之间的水平距离BE 为5 m,小明的眼睛与地面的距离AB 为1.5 m,那么这棵树高是4・39m.(可用计算器，精确到0.01)11. 如图，E 为口ABCD 的DC 边延长线上一点，连接AE,交BC 于点F,则'图中与AABF 相似的三 角形共有2个.D. 3^2A 2 B.| D. 1B. 2^2 C 4CD 平分 ZBCE, BC=2书,贝AB =4.8$60。

课时训练(二十二)锐角三角函数及其应用(限时:40分钟)|夯实基础|1.[2018·天津] cos30°的值等于()A.22B.32C.1D.32.[2018·益阳] 如图K22-1,小刚从山脚A出发,沿坡角为α的山坡向上走了300米到达B点,则小刚上升了()图K22-1A.300 sinα米B.300 cosα米C.300 tanα米D.300米3.[2018·金华、丽水] 如图K22-2,两根竹竿AB和AD斜靠在墙CE上,量得∠ABC=α,∠ADC=β,则竹竿AB与AD的长度之比为()图K22-2A.B.ss C.ssD.coscos4.[2018·日照] 如图K22-3,边长为1的小正方形构成的网格中,半径为1的☉O的圆心O在格点上,则∠BED的正切值等于()图K22-3A.2B.C.2D.125.[2018·娄底] 如图K22-4,由四个全等的直角三角形围成的大正方形的面积是169,小正方形的面积为49,则sinα-cosα=()图K22-4A.13B.-13C.13D.-136.[201 ·滨州] 如图K22-5,在△ABC中,AC⊥BC,∠ABC=30°,点D是CB延长线上的一点,且BD=BA,则tan∠DAC的值为()图K22-5A.2+B.2C.3+D.37.[2018·滨州] 在△ABC中,∠C=90°,若tan A=12,则sin B= .8.[2018·咸宁] 如图K22-6,航拍无人机从A处测得一幢建筑物顶部的仰角为4 °,测得底部C的俯角为60°,此时航。

2019年中考复习单元测试（四）图形的初步认识与三角形(含答案)单元测试(四) 图形的初步认识与三角形(时间：45分钟满分：100分)一、选择题(每小题4分，共32分)1．下列各组数中，不可能成为一个三角形三边长的是(C)A．3，4，5 B．5，7，7 C．5，6，12 D．5，12，132．下列各图中，∠1与∠2互为余角的是(B)3．如图，字母B所代表的正方形的面积是(B)A．12 B．144 C．13 D．1944．如图，快艇从P处向正北航行到A处时，向左转50°航行到B处，再向右转80°继续航行，此时的航行方向为(A)A．北偏东30° B．北偏东80° C．北偏西30° D．北偏西50°5．如图，点D，E分别在线段AB，AC上，CD与BE相交于点O，已知AB＝AC，现添加以下哪个条件仍不能判定△ABE≌△ACD(D)A．∠B＝∠C B．AD＝AE C．BD＝CE D．BE＝CD6．已知直线a∥b，将一块含45°角的直角三角板(∠C＝90°)按如图所示的位置摆放．若∠1＝55°，则∠2的度数为(A)A．80° B．70° C．85° D．75°7．如图，在△ABC 中，AC ＝8，∠ABC＝60°，∠C＝45°，AD⊥BC，垂足为D ，∠ABC 的平分线交AD 于点E ，则AE 的长为(C )A.432 B ．2 2 C.832 D ．3 28．如图，E ，F 是▱ABCD 对角线上AC 两点，AE ＝CF ＝14AC.连接DE ，DF 并延长，分别交AB ，BC 于点G ，H ，连接GH ，则S △ADGS △BGH的值为(C ) A.12 B.23 C.34D ．1二、填空题(每小题4分，共24分)9．如图，在△ABC 中，∠ACB＝90°，CD∥AB，∠ACD＝40°，则∠B 的度数为50__°．10．如图所示，小明同学利用一个锐角是30°的三角板测量一棵树的高度，测量时如图所示放置三角板，已知他与树之间的水平距离BE 为5 m ，小明的眼睛与地面的距离AB 为1.5 m ，那么这棵树高是4.39m.(可用计算器，精确到0.01)11．如图，E 为▱ABCD 的DC 边延长线上一点，连接AE ，交BC 于点F ，则图中与△ABF 相似的三角形共有2个．12．如图，在Rt △ABC 中，∠ACB＝90°，D ，E 是边AB 上两点，且CE 所在直线垂直平分线段AD ，CD 平分∠BCE，BC ＝23，则AB ＝4．13．如图，在△ABC 中，BF 平分∠ABC，AF⊥BF 于点F ，D 为AB 的中点，连接DF 并延长交AC 于点E.若AB ＝10，BC ＝16，则线段EF 的长为3．14．一般地，当α，β为任意角时，sin (α＋β)与sin (α－β)的值可以用下面的公式求得：sin (α＋β)＝sin α·cos β＋cos α·sin β；sin (α－β)＝sin α·c os β－cos α·sin β.例如sin 90°＝sin (60°＋30°)＝sin 60°·cos 30°＋cos 60°·sin 30°＝32×32＋12×12＝1.类似地，可以求得sin 4三、解答题(共44分)15．(10分)如图，点E ，F 在BC 上，BE ＝CF ，AB ＝DC ，∠B＝∠C，AF 与DE 相交于点G ，求证：GE ＝GF.证明：∵BE ＝CF ， ∴BE ＋EF ＝CF ＋EF. ∴BF ＝CE.在△ABF 和△DCE 中， ⎩⎪⎨⎪⎧AB ＝DC ，∠B ＝∠C，BF ＝CE ，∴△ABF≌DCE (SAS )． ∴∠GEF ＝∠GFE. ∴EG ＝FG.16．(10分)下面有4张形状、大小完全相同的方格纸，方格纸中的每个小正方形的边长都是1，请在方格纸中分别画出符合要求的图形，所画图形各顶点必须与方格纸中小正方形的顶点重合，具体要求如下：(1)画一个直角边长为4，面积为6的直角三角形； (2)画一个底边长为4，面积为8的等腰三角形； (3)画一个面积为5的等腰直角三角形；(4)画一个边长为22，面积为6的等腰三角形．,(1)) ,(2)),(3)),(4))解：如图．17．(12分)如图所示，某公路检测中心在一事故多发地段安装了一个测速仪器，检测点设在距离公路10 m 的A 处，测得一辆汽车从B 处行驶到C 处所用时间为0.9 s 秒，已知∠B＝30°，∠C＝45°.(1)求B ，C 之间的距离；(保留根号)(2)如果此地限速为80 km /h ，那么这辆汽车是否超速？请说明理由．(参考数据：3≈1.7，2≈1.4)解：(1)过点A 作AD⊥BC 于点D ，则AD ＝10 m ， 在Rt△ACD 中， ∵∠C ＝45 °， ∴AD ＝CD ＝10 m.在Rt△ABD 中，∵∠B ＝30 °， ∴tan30 °＝ADBD.∴BD ＝3AD ＝10 3 m.∴BC ＝BD ＋DC ＝(10＋103)m. (2)结论：这辆汽车超速．理由：∵BC ＝10＋103≈27(m )，∴汽车速度为270.9＝30(m/s )＝108(km/h )．∵108>80，∴这辆汽车超速．18．(12分)问题1：如图1，在△ABC 中，AB ＝4，D 是AB 上一点(不与A ，B 重合)，DE∥BE，交AC 于点E ，连接CD.设△ABC 的面积为S ，△DEC 的面积为S′.(1)当AD ＝3时，S′S ＝316；(2)设AD ＝m ，请你用含字母m 的代数式表示S′S.问题2：如图2，在四边形ABCD 中，AB ＝4，AD∥BC，AD ＝12BC ，E 是AB 上一点(不与A ，B 重合)，EF∥BC，交CD 于点F ，连接CE.设AE ＝n ，四边形ABCD 的面积为S ，△EFC 的面积为S′.请你利用问题1的解法或结论，用含字母n 的代数式表S′S.图1 图2解：问题1：(2)∵AB ＝4，AD ＝m ，∴AD ＝4－m. ∵DE∥BC，∴CE EA ＝BD DA ＝4－m m .∴S △DEC S △ADE ＝4－mm .又∵DE∥BC，∴△ADE∽△ABC. ∴S △ADE S △ABC ＝(m 4)2＝m216. ∴S △DEC S △ABC ＝S △DEC S △ADE ·S △ADE S △ABC ＝4－m m ·m 216＝－m 2＋4m 16， 即S ′S ＝－m 2＋4m 16.问题2：分别延长BA ，CD ，相交于点O. ∵AD∥BC，∴△OAD∽△OBC.∴OA OB ＝AD BC ＝12. ∴OA ＝AB ＝4.∴OB ＝8. ∵AE ＝n ，∴OE ＝4＋n. ∵EF∥BC.由问题1的解法可知，S △CEF S △OBC ＝S △CEF S △OEF ·S △OEF S △OBC ＝4－n 4＋n ·(4＋n 8)2＝16－n264.∵S △OAD S △OBC ＝(OA OB )2＝14，∴S 四边形ABCD S △OBC ＝34. ∴S △CEFS 四边形ABCD ＝S △CEF 34S △OBC ＝43×16－n 264＝16－n248， 即S ′S ＝16－n 248.。

课时训练(二十二)锐角三角函数及其应用|夯 实 基 础|一、选择题1．[2017·天津]cos60°的值等于( ) A. 3 B ．1 C.22 D.122．[2017·湖州]如图K22－1，已知在Rt △ABC 中，∠C ＝90°，AB ＝5，BC ＝3，则cosB 的值是( )A.35B.45C.34D.43K22－1K22－23．[2017·宜昌]△ABC 在网格中的位置如图K22－2所示(每个小正方形边长为1)，AD ⊥BC 于D ，下列选项中，错误的是( )A ．sin α＝cos αB ．tanC ＝2 C ．sin β＝cos βD ．tan α＝14．[2017·益阳]如图K22－3，电线杆CD 的高度为h ，两根拉线AC 与BC 相互垂直，∠CAB ＝α，则拉线BC 的长度为(A 、D 、B 在同一条直线上)( )A.h sin αB.h cos αC.htan αD ．h ·cos αK22－3K22－45．[2017·兰州]如图K22－4，一个斜坡长130 m ，坡顶离水平地面的距离为50 m ，那么这个斜坡与水平地面夹角的正切值等于( )A.513 B.1213 C.512 D.1312图K22－56．[2017·滨州]如图K22－5，在△ABC 中，AC ⊥BC ，∠ABC ＝30°，点D 是CB 延长线上的一点，且BD ＝BA ，则tan ∠DAC 的值为( )A ．2＋ 3B ．2 3C ．3＋ 3D ．3 3 二、填空题7．[2017·烟台]在Rt △ABC 中，∠C ＝90°，AB ＝2，BC ＝3，则sin A2＝________．8．[2017·宁波]如图K22－6，一名滑雪运动员沿着倾斜角为34°的斜坡，从A 滑行至B ，已知AB ＝500米，则这名滑雪运动员的高度下降了________米．(参考数据：sin34°≈0.56，cos34°≈0.83，tan34°≈0.67)K22－6K22－79．[2017·临沂]如图K22－7，在▱ABCD 中，对角线AC ，BD 相交于点O.若AB ＝4，BD ＝10，sin ∠BDC ＝35，则▱ABCD的面积是________．三、解答题10．[2017·衡阳]衡阳市城市标志来雁塔坐落在衡阳市雁峰公园内．如图K22－8，为了测量来雁塔的高度，在Ε处用高为1.5米的测角仪AE ，测得塔顶C 的仰角为30°，再向塔身前进10.4米，又测得塔顶C 的仰角为60°，求来雁塔的高度．(结果精确到0.1米)图K22－811.[2017·郴州]如图K22－9所示，C 城市在A 城市正东方向，现计划在A 、C 两城市间修建一条高速铁路(即线段AC)，经测量，森林保护区的中心P 在A 城市的北偏东60°方向上，在线段AC 上距A 城市120 km 的B 处测得P 在北偏东30°方向上，已知森林保护区是以点P 为圆心，100 km 为半径的圆形区域，请问计划修建的这条高速铁路是否穿越保护区，为什么？(参考数据：3≈1.73)图K22－912．[2017·常德]图K22－10①②分别是某款篮球架的实物图与示意图，已知底座BC ＝0.60米，底座BC 与支架AC 所形成的角∠ACB＝75°，支架AF 的长为2.50米，篮板顶端F 点到篮筐D 的距离FD ＝1.35米，篮板底部支架HE 与支架AF 所成的角∠FHE＝60°，求篮筐D 到地面的距离(精确到0.01米)．(参考数据：cos75°≈0.2588，sin75°≈0.9659，tan75°≈3.732，3≈1.732，2≈1.414)图K22－1013．[2017·长沙]为了维护国家主权和海洋权利，海监部门对我国领海实现了常态化巡航管理，如图K22－11，正在执行巡航任务的海监船以每小时50海里的速度向正东方向航行，在A 处测得灯塔P 在北偏东60°方向上，继续航行1小时到达B 处，此时测得灯塔P 在北偏东30°方向上．(1)求∠APB 的度数；(2)已知在灯塔P 的周围25海里内有暗礁，问海监船继续向正东方向航行是否安全？图K22－11|拓 展 提 升|14．[2017·舟山]如图K22－12，把n 个边长为1的正方形拼接成一排，求得tan ∠BA 1C ＝1，tan ∠BA 2C ＝13，tan∠BA 3C ＝17，计算tan ∠BA 4C ＝______，…，按此规律，写出tan ∠BA n C ＝________(用含n 的代数式表示)．图K22－1215．如图K22－13，根据图中数据完成填空，再按要求答题：图K22－13sin 2A 1＋sin 2B 1＝________；sin 2A 2＋sin 2B 2＝________；sin 2A 3＋sin 2B 3＝________.(1)观察上述等式，猜想：在Rt △ABC 中，∠C ＝90°，都有sin 2A ＋sin 2B ＝________；(2)如图④，在Rt △ABC 中，∠C ＝90°，∠A ，∠B ，∠C 的对边分别是a ，b ，c ，利用三角函数的定义和勾股定理，证明你的猜想；(3)已知∠A＋∠B＝90°，且sinA ＝513，求sinB.参考答案1．D2．A [解析] 在Rt △ABC 中，cosB ＝邻边斜边＝BC AB ＝35.3．C [解析] sin α＝cos α＝22 2＝12，tanC ＝21＝2，sin β＝cos(90°－β)，故选C.4．B [解析] 根据同角的余角相等得，∠CAD ＝∠BCD，由cos ∠BCD ＝CD BC ，知BC ＝CD cos ∠BCD ＝hcos α，因此选B.5．C [解析] 在直角三角形中，根据勾股定理可知水平的直角边长度为120 m ，正切值为对边比邻边，故斜坡与水平地面夹角的正切值等于50120＝512，故选C.6．A [解析] 设AC ＝a ，则AB ＝a÷sin30°＝2a ，BC ＝a ÷tan30°＝3a ，∴BD ＝AB ＝2a.∴tan ∠DAC ＝DCAC ＝（2＋3）aa＝2＋ 3. 7.12 [解析] 在Rt △ABC 中，∠C ＝90°，AB ＝2，BC ＝3，∴sinA ＝32，∴∠A ＝60°. ∴sin A 2＝12.8．280 [解析] 在Rt △ABC 中，sinB ＝ACAB，∴AC ＝ABsin34°≈500×0.56＝280.9．24 [解析] 过C 作CE⊥BD 于E ，在Rt △CDE 中，∵sin ∠BDC ＝35＝CE CD ＝CE AB ，AB ＝4，∴CE ＝125，∴S ▱ABCD ＝2×12×BD×CE＝24.10．解：因为∠CBD＝60°，∠CAD ＝30°， 所以∠ACB＝30°，所以AB ＝BC ＝10.4米．在直角三角形CBD 中，BC ＝10.4米，∠CBD ＝60°，所以CD ＝BC×sin ∠CBD ＝10.4×32≈9.0(米)，所以塔高为9.0＋1.5＝10.5(米)． 答：来雁塔的高度约为10.5米．11．解：如图，过点P 作PH⊥AC，交AC由题意得∠EAP＝60°，∠FBP ＝30°， ∴∠PAB ＝30°，∠PBH ＝60°， ∴∠APB ＝30°，∴AB ＝PB ＝120，∴在Rt △PBH 中，PH ＝PBsin ∠PBH ＝120×sin60°＝60 3≈103.8， ∵103.8＞100，∴要修建的这条高速铁路不会穿越森林保护区．12．解：如图，过点A 作AM⊥FE 交FE ∵∠FHE ＝60°，∴∠F ＝30°.在Rt △AFM 中，FM ＝AF·cosF ＝AF·cos30°＝2.50×32≈2.165(米)． 在Rt △ABC 中，AB ＝BC·tan ∠ACB ＝BC·tan75°≈0.60×3.732＝2.2392(米)． ∴篮板顶端F 点到地面的距离为：FM ＋AB ＝2.165＋2.2392＝4.4042(米)， ∴篮筐D 到地面的距离为：4.4042－FD ＝4.4042－1.35＝3.0542≈3.05(米)． 13．解：(1)∵∠PAB＝30°，∠ABP ＝120°， ∴∠APB ＝180°－∠PAB－∠ABP＝30°. (2)作PH⊥AB 于H.∵∠BAP ＝∠BPA＝30°， ∴BA ＝BP ＝50，在Rt △PBH 中，PH ＝PB·sin60°＝50×32＝25 3，∵25 3>25，∴海监船继续向正东方向航行是安全的．14.113 1n 2－n ＋1 [解析] 过点C 作CH⊥BA 4于H ，由勾股定理得BA 4＝42＋12＝17， A 4C ＝32＋12＝10，∵△BA 4C 的面积＝4－12×1×4－12×1×3＝12，∴12×17CH ＝12，∴CH ＝1717， 则A 4H ＝A 4C 2－CH 2＝13 1717， ∴tan ∠BA 4C ＝CH A 4H ＝171713 1717＝113，∵1＝12－1＋1，3＝22－2＋1，7＝32－3＋1，13＝42－4＋1，∴tan ∠BA n C ＝1n 2－n ＋1.15．解： 1 1 1 (1)1(2)证明：在Rt △ABC 中，∠C ＝90°.∵sinA ＝a c ，sinB ＝bc，∴sin 2A ＋sin 2B ＝a 2＋b 2c2.∵∠C ＝90°，∴AC 2＋BC 2＝AB 2，即a 2＋b 2＝c 2，∴sin 2A ＋sin 2B ＝1.(3)∵sinA ＝513，sin 2A ＋sin 2B ＝1，∴sinB ＝1－⎝ ⎛⎭⎪⎫5132＝1213.。

课时训练(二十二) 锐角三角函数及其应用|夯实基础|1.[2018·云南] 在Rt△ABC中,∠C=90°,AC=1,BC=3,则∠A的正切值为()图K22-1A.3B.C.D.2.[2017·宜昌] △ABC在网格中的位置如图K22-1所示(每个小正方形边长为1),AD⊥BC于D,下列选项中,错误的是()A.sin α=cos αB.tan C=2C.sin β=cos βD.tan α=13.在△ABC中,∠A,∠B都是锐角,tan A=1,sin B=,你认为对△ABC最确切的判断是()A.等腰三角形B.等腰直角三角形C.直角三角形D.锐角三角形4.[2018·日照] 如图K22-2,边长为1的小正方形构成的网格中,半径为1的☉O的圆心O在格点上,则∠BED的正切值等于()图K22-222 A . B. C .2 D .5.[2018·重庆B 卷] 如图K22-3,AB 是一垂直于水平面的建筑物.某同学从建筑物底端B 出发,先沿水平方向向右行走20米到达点C ,再经过一段坡度(或坡比)为i=1∶0.75、坡长为10米的斜坡CD 到达点D ,然后再沿水平方向向右行走40米到达点E (A ,B ,C ,D ,E 均在同一平面内).在E 处测得建筑物顶端A 的仰角为24°,则建筑物AB 的高度约为(参考数据:sin 24°≈0.41,cos 24°≈0.91,tan 24°≈0.45) ()图K22-3A .21.7米B .22.4米C .27.4米D .28.8米6.把sin 60°,cos 60°,tan 60°按从小到大的顺序排列7.[2018·黄石] 如图K22-4,无人机在空中C 处测得地面度CD 为100米,点A ,D ,B 在同一水平直线上,则A ,B 两点间的距离是图K22-48.[2018·潍坊]如图K22-5,一艘渔船正以60海里/时的速度向正东方向航行,在A 处测得岛礁P 在东北方向上,继续航行1.5小时后到达B 处,此时测得岛礁P 在北偏东30°方向,同时测得岛礁P 正东方向上的避风港M 在北偏东60°方向.为了在台风到来之前用最短时间到达M 处,渔船立刻加速以75海里/时的速度继续航行 小时即可到达.(结果保留根号)图K22-59.[2017·舟山] 如图K22-6,把n个边长为1的正方形拼接成一排,求得tan∠BA1C=1,tan∠BA2C=,tan∠BA3C=,tan ∠BA4C= ,…,按此规律,tan∠BA n C= (用含n的代数式表示).图K22-610.[2017·丽水] 图K22-7是某小区的一个健身器材平面图,已知BC=0.15 m,AB=2.7 m,∠BOD=70°,求端点A到地面CD的距离(精确到0.1 m,参考数据:sin 70°≈0.94,cos 70°≈0.34,tan 70°≈2.75)图K22-711.[2018·台州] 如图K22-8是一辆吊车的工作示意图,AC是可以伸缩的起重臂,其转动点A离地面BD的高度AH 为3.4 m.当起重臂AC长度为9 m,张角∠HAC为118°时,求操作平台C离地面的高度(结果保留小数点后一位;参考数据:sin 28°≈0.47,cos 28°≈0.88,tan 28°≈0.53).图K22-834 4 12.[2018·内江] 如图K22-9是某路灯在铅垂面内的示意图,灯柱AC的高为11米,灯杆AB与灯柱AC的夹角∠A=120°,路灯采用锥形灯罩,在地面上的照射区域DE长为18米,从D,E两处测得路灯B的仰角分别为α和β,且tan α=6,tan β=.求灯杆AB的长度.图K22-9|拓展提升|13.如图K22-10,已知AD∥BC,AB⊥AD,点E,F分别在射线AD,BC上,若点E与点B关于AC对称,点E与点F关于BD 对称,AC与BD相交于点G,则()A.1+tan∠ADB=B.2BC=5CFC.∠AEB+22°=∠DEFD.4cos∠AGB=图K22-1014.如图K22-11,在每一个四边形ABCD中,均有AD∥BC,CD⊥BC,∠ABC=60°,AD=8,BC=12.(1)如图①,点M是四边形ABCD的边AD上一点,求△BMC的面积.(2)如图②,点N是四边形ABCD边AD上的任意一点,请你求出△BNC周长的最小值.(3)如图③,在四边形ABCD的边AD上,是否存在一点P,使得cos∠BPC的值最小?若存在,求出此时cos∠BPC的值;若不存在,请说明理由.图K22-1156 6 参考答案1.A[解析] 根据正切的定义得tan A==3.2.C[解析] 先构建直角三角形,再根据三角函数的定义计算,sin α=cos α==,tanC==2,sinβ=cos(90°-β),tan α=1,故选C.3.B4.D[解析] 在Rt△ABC中,AB=2,BC=1,∴tan∠BAC==.∵∠BED=∠BAD,∴tan∠BED=.故选D.5.A[解析] 过点C作CN⊥DE于点N,延长AB交ED于点M,则BM⊥DE于点M,则MN=BC=20米.∵斜坡CD的坡比i=1∶0.75,∴令CN=x米,则DN=0.75x米.在Rt△CDN中,由勾股定理,得x2+(0.75x)2=102,解得x=8,从而CN=8米,DN=6米.∵DE=40米,∴ME=MN+ND+DE=66(米),AM=(AB+8)米.在Rt△AME中,tan E=,即=tan24°,从而0.45=,解得AB=21.7(米),故选A.6.cos 60°<sin 60°<tan 60°7.100(1+)[解析] 由题意可知∠A=60°,∠B=45°,∴AD==100米,BD=CD=100米,∴AB=AD+BD=100+100=100(1+)米.8.[解析] 过点P作PQ⊥AB,垂足为Q,过点M作MN⊥AB,垂足为N.AB=60×1.5=90(海里).设PQ=MN=x,由点P在点A的东北方向可知,∠PAQ=45°,∴AQ=PQ=x,BQ=x-90.在Rt△PBQ中,∠PBQ=90°-30°=60°,tan60°==,解得x=135+45.在Rt△BMN中,∠MBN=90°-60°=30°,∴BM=2MN=2x=2×(135+45)=270+90.∴航行时间为=(小时).9.[解析] 根据所给的三角函数值进行分析可以得到如下规律:tan∠BA1C==,tan∠BA2C==,tan∠BA3C==,tan∠BA4C==,….按此规律tan∠BA n C==.10.[解析] 过点A作AE⊥CD于点E,过点B作BF⊥AE于点F,构造Rt△ABF,运用解直角三角形的知识求出AF,进而求出AE,得出结果.解:过点A作AE⊥CD于点E,过点B作BF⊥AE于点F,∵OD⊥CD,∴AE∥OD,∴∠A=∠BOD=70°.在Rt△ABF中,AB=2.7,∴AF=2.7×cos70°≈2.7×0.34=0.918,∴AE=AF+BC=0.918+0.15=1.068≈1.1.788 答:端点A 到地面CD 的距离约是1.1 m .11.解:如图所示,过点C 作CF ⊥BD ,垂足为F ,过点A 作AE ⊥CF ,垂足为E,∵AE ⊥CF ,∴∠AEC=90°,在Rt △AEC 中,sin ∠CAE=,可得CE=AC ·sin ∠CAE ≈9×0.47=4.23.∵∠AHF=∠EFH=∠AEF=90°,∴四边形AHFE 是矩形, ∴EF=AH=3.4,∴CF=CE+EF=3.4+4.23=7.63≈7.6(米). 答:操作平台C 离地面的高度为7.6米.12.解:如图,过点B 作BH ⊥DE ,垂足为点H ,过点A 作AG ⊥BH ,垂足为点G. ∵BH ⊥DE ,∴∠BHD=∠BHE=90°. 在Rt △BHD 中,tan α==6,在Rt △BHE 中,tan β==,∴BH=6DH,BH=EH,∴8DH=EH.∵DE=18,DE=DH+EH,∴9DH=18,∴DH=2,BH=12.∵∠BHD=∠AGH=∠ACH=90°,∴四边形ACHG为矩形,∴AC=GH=11,∠CAG=90°,BG=BH-GH=12-11=1,∵∠BAC=120°,∴∠BAG=∠BAC-∠CAG=120°-90°=30°.∴在Rt△AGB中,AB=2BG=2.答:灯杆AB的长度为2米.13.A[解析] 如图,连结CE,设EF与BD相交于点O.由对称性,得AB=AE.设AB=1,则BE==.∵点E与点F关于BD对称,∴BE=BF,∠EBD=∠FBD,又∵∠EDB=∠DBF,∴∠EBD=∠EDB,∴DE=BE=,∴AD=1+.∵AD∥BC,AB⊥AD,AB=AE,∴四边形ABCE是正方形,91010 ∴BC=AB=1,1+tan ∠ADB=1+=1+-1=,故A 正确.∵CF=BF-BC=-1,2BC=2×1=2,5CF=5(-1),∴2BC ≠5CF ,故B 错误. ∠AEB+22°=45°+22°=67°,在Rt △ABD 中,BD===,sin ∠DEF===.用计算器计算可得 ∠DEF=67.5°,故C 错误.由勾股定理得OE 2=()2-2=,∴OE=.∵∠EBG+∠AGB=90°, ∠EBG+∠BEF=90°, ∴∠AGB=∠BEF. 又∵∠BEF=∠DEF ,∴4cos ∠AGB=4×=4×=2,故D 错误.14.解:(1)过点A 作AE ⊥BC ,垂足为E. 在Rt △ABE 中,∠ABC=60°,BE=12-8=4, ∴AE=4,∴S△BMC =BC·AE=×12×4=24.(2)作点C关于AD对称的点C',连结BC'交AD于点N,点N为满足条件的点.易知CN=C'N.在Rt△CBC'中,BC=12,CC'=8,∴BC'==4,∴△BCN周长的最小值为12+4.(3)存在点P,使得cos∠BPC的值最小.如图,作BC的垂直平分线PQ交BC于点Q,交AD于点P,连结BP,CP,作△BPC的外接圆☉O,☉O与直线PQ交于点N,又PB=PC,∴圆心O在PN上.∵AD∥BC,∴AD为☉O的切线,切点为P.∵PQ=DC=4>6,∴圆心O在弦BC的上方.在AD上任取一点P',连结P'C,P'B,P'B交☉O于点M,连结MC,∴∠BPC=∠BMC≥∠BP'C,∴∠BPC最大,此时cos∠BPC的值最小.连结BO,在Rt△BOQ中,易知BO=4-OQ,BQ=6,11∴OQ=,∴OB=,∴cos∠BPC=cos∠BOQ=.故cos∠BPC 的最小值是.1212。