第八章 杆件的扭转

9
8.3 平面弯曲梁的变形计算———叠加法（查表法） 从上一节例题可以看出，由于梁的变形微小， 而且梁的材料是在线弹性范围内工作的，因此梁的 挠度和转角均与梁上的荷载成线性关系。这样，梁 上某一荷载所引起的变形，不受同时作用的其他荷 载的影响，即各荷载对弯曲变形的影响是各自独立 的。因此，梁在几项荷载（集中力、集中力偶或分 布力）同时作用下某一截面的挠度和转角，就分别 等于每一项荷载单独作用下给截面的挠度和转角的 叠加。当每一项荷载所引起的转角在同一平面内（ 例如均在 xy平面内），其挠度都在同一方向上（ 例如均在 y轴方向）时，叠加就是代数和。
12
小结 本章主要研究扭转轴和平面弯曲梁的变形计算 和刚度校核问题。 1）扭转轴的变形计算及刚度条件为
13
2）平面弯曲梁的变形计算可用积分法和叠加 法进行。用积分法求解梁变形就是正确列出各段梁 的弯矩方程，代入挠曲线近似微分方程，积分一次 得到转角方程，再积分一次得到挠曲线方程，然后 正确应用边界条件和连续条件确定积分常数。积分 法是求梁变形的基本方法，虽然计算比较烦琐，但 在理论上是比较重要的。
14
2
图 8.2
3
图 8.3
4
5
6
7
8
正文正文正文正文正文正文正文正文正文正文 正文正文正文正文正文正文正文正文正文正文正文 正文正文正文正文正文正文正文正文正文正文正文 正文正文正文正文正文正文正文正文正文正文正文 正文正文正文正文正文正文正文正文正文正文正文 正文正文正文正文正文正文正文正文正文正文
第8章 杆件的变形和刚度校核
为了避免受扭的轴产生过大的变形，除了要 保证强度条件以外，还要满足刚度要求。工程中 ，通常是用单位长度扭转角 θ 来限制轴的扭转变 形。因此，其刚度条件为

机械运作原理的杆件弯曲与扭转分析杆件弯曲与扭转分析是机械运作原理中的重要内容之一。

对于机械结构而言，杆件的弯曲与扭转是不可避免的力学现象，而准确地分析和计算杆件在弯曲与扭转力下的应力和变形是确保机械结构安全可靠运行的重要步骤。

下面将对杆件弯曲与扭转的原理进行详细分析。

首先，我们来讨论杆件的弯曲。

在杆件的弯曲分析中，我们通常采用梁理论（也称为Euler- Bernoulli梁理论）进行分析。

根据这一理论，当杆件受到作用力时，杆件会发生弯曲变形，即杆件上的任意一点都会产生弯曲位移。

杆件的弯曲会引起杆件上的各个截面产生弯矩，而弯矩又会导致杆件上的截面发生应力分布。

根据材料力学的知识，我们可以得到杆件截面上的应力与弯矩的关系：弯曲应力与弯矩成正比。

其次，我们来讨论杆件的扭转。

在杆件扭转分析中，我们通常采用圆柱体的扭转理论进行分析。

根据这一理论，当杆件受到扭矩时，杆件会发生扭转变形。

扭转时，杆件截面上的各个点会绕着杆件中心线产生相对位移。

根据材料力学的知识，我们可以得到杆件截面上的应力与扭矩的关系：扭转应力与扭矩成正比。

综上所述，对于杆件的弯曲与扭转分析，我们首先需要确定杆件所受的力或扭矩，并根据梁理论和扭转理论计算出杆件截面上的弯矩和扭矩。

然后，根据材料的力学性质，将弯矩和扭矩转换成截面上的应力值，并计算出截面上的应力分布情况。

最后，根据杆件所受力的大小和截面上的应力分布情况，判断杆件是否满足运行要求，如果杆件的应力超过了材料的强度极限，就需要进行结构优化或者选择更合适的材料。

需要注意的是，杆件的弯曲和扭转往往是同时存在的，因此在分析时需要将两者综合考虑。

当杆件同时受到弯曲力和扭矩时，会出现综合应力状态，即弯曲应力和扭转应力的叠加效应。

对于综合应力状态的杆件分析，我们可以使用叠加原理进行计算。

杆件弯曲与扭转分析在机械工程中是一项基础而重要的工作，它能够帮助我们理解和分析杆件在工作过程中的变形和应力状态，为设计和优化机械结构提供重要的理论依据。

解析法适用于简单杆件的简单边界条 件，通过数学推导得到精确解。
边界元法是一种与有限元法类似的数 值方法，适用于具有复杂边界条件的 杆件扭转问题。
03
杆件扭转的实验研究
实验设备与材料
扭矩计
用于测量杆件在扭转过程中的扭矩。
不同直径和材料的杆件
用于研究不同参数对杆件扭转的影响。
杠杆
用于固定和支撑杆件，确保其稳定。
采矿工程
矿山的支架、提升机等设备需要考虑杆件扭转问 题，以确保矿山的安全生产和正常运行。
水利工程
大坝、水闸等水利设施需要考虑杆件扭转问题， 以确保水利设施的正常运行和安全性。
05
杆件扭转的研究展望
新型材料的杆件扭转性能研究
总结词
随着新材料技术的不断发展，新型材料的杆件在扭转性能方面具有广阔的研究前景。
全性。
高层建筑
高层建筑的柱、梁等结构部件在风 力、地震等外力作用下，容易发生 杆件扭转，影响建筑物的安全性能 。
建筑加固
对于已经存在的建筑物，如果存在 杆件扭转问题，需要进行加固处理 ，以增强其承载能力和稳定性。
机械系统中的杆件扭转问题
01悬挂系 统等部位需要考虑杆件扭 转问题，以确保车辆的正 常运行和安全性。
通过引入传感器、智能算法和机器学习等技 术，可以实现杆件的智能化监测、控制和优 化设计。例如，利用传感器监测杆件的扭转 状态，通过智能算法分析其力学性能和稳定 性，并根据分析结果进行优化设计。未来研 究可以进一步探索智能化技术在杆件扭转领 域的应用，以提高杆件的设计水平和应用范
围。
THANKS
感谢观看
详细描述
新型材料如碳纤维复合材料、钛合金等具有轻质、高强度等优点，在杆件扭转性能方面表现出 优异的力学性能。未来研究可以探索这些新型材料的杆件在复杂环境下的扭转性能，以及如何 优化设计以提高其扭转刚度和稳定性。

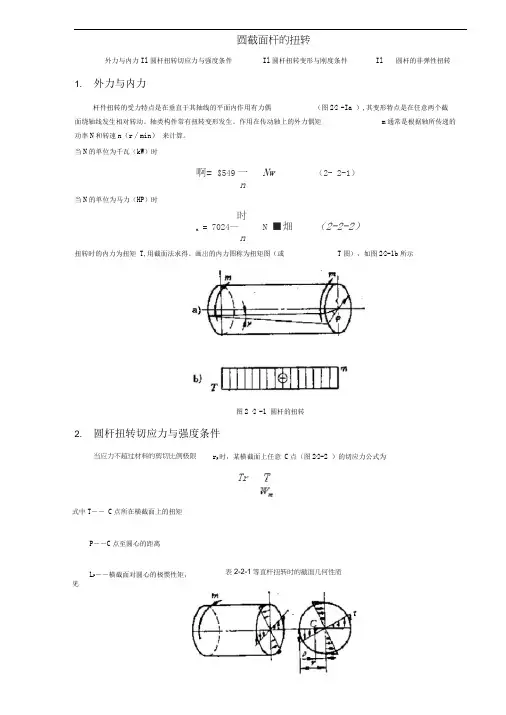
圆截面杆的扭转外力与内力Il圆杆扭转切应力与强度条件Il圆杆扭转变形与刚度条件Il 圆杆的非弹性扭转1. 外力与内力杆件扭转的受力特点是在垂直于其轴线的平面内作用有力偶（图2∙2 -Ia ）,其变形特点是在任意两个截面绕轴线发生相对转动。

轴类构件常有扭转变形发生。

作用在传动轴上的外力偶矩m通常是根据轴所传递的功率N和转速n（r∕min）来计算。

当N的单位为千瓦（kW）时啊= $549一Nw（2- 2-1）n当N的单位为马力（HP）时时m= 7024—N■畑（2-2-2）n扭转时的内力为扭矩T,用截面法求得。

画岀的内力图称为扭矩图（或T图），如图2∙2-1b所示图2 ∙2 -1 圆杆的扭转2. 圆杆扭转切应力与强度条件r p时，某横截面上任意C点（图2∙2-2 ）的切应力公式为Tr式中T―― C点所在横截面上的扭矩P――C点至圆心的距离L P――横截面对圆心的极惯性矩，见当应力不超过材料的剪切比例极限表2-2-1等直杆扭转时的截面几何性质图2 ∙2 -2 切应力分布圆杆横截面上的切应力 r 沿半径呈线性分布，其方向垂直于半径（图 周各点上，其计算公式为丁二至 （2-2-A ）等截面杆的最大切应力发生在T maX 截面（危险截面）的圆周各点（危险点）上。

其强度条件为≤［r ］C2-2— 了）式中，［T ］为许用扭转切应力，与许用拉应力［σ ］的关系为：［T ］= （0.5〜0.6 ）［ σ ］（塑性材料）或［T ］= （0.50.6 ） ［ σ ］（脆性材料）3.圆杆扭转变形与刚度条件在比弹性范围内，圆杆在扭矩T 作用下，相中为 L 的两截面间相对扭转角为式中,［θ ］为圆杆的许用单位扭转角（°） /m4.圆杆的非弹性扭转讨论圆杆扭转时切应力超过材料的比例极限并进入塑性状态的情况。

对于加工硬化材料，如果材料的应2 ∙3 -2 ）。

模截面上的最大切应力在圆 式中G ――材料的切变模量 单位扭转角公式为式中GL P 抗扭刚度圆杆上与杆轴距离为 P 外（图 rad (2-2-6)180毋二一π2 ∙2 -2 TIT—Cy 阳 (JLF）的切应变r 为(2-2-7)(2(2-2-9)圆杆表面处的最大切应变为”二扈¢2-2-10)式中,r ——圆杆的半径等截面圆杆的最大单位扭转角，发生在 段内, 其刚度条件为ISOεj HbSKJZ r尹］(2- 2-12)相应的切应力r max可以从应力-应变图求得。

T2 = −m2 − m3 = −(4.78 + 4.78) = −9.56kN ⋅ m
×
③绘制扭矩图
m2
m3
m1
m4
n A
扭矩图
B
C
⊕
D
6.37kN.m
–
4.78kN.m
–
9.56kN.m
T
max
= 9.56 kN ⋅ m, BC段为危险截面。 段为危险截面。 段为危险截面
×
画图示杆的扭矩图。 例5 画图示杆的扭矩图。
×
三、剪切虎克定律： 剪切虎克定律： 单元体ab 的倾角γ 称为切应变 切应变， 单元体 的倾角γ 称为切应变， 切应变是单元体直角的改变量 单元体直角的改变量。 切应变是单元体直角的改变量。实 验表明，在弹性范围内， 验表明，在弹性范围内，切应力与 dy 切应变成正比， 切应变成正比，即 a
γ τ´
×
⒋ 极惯性矩
dρ
I p = ∫ A ρ 2 dA = ∫ ρ 2 ⋅ 2 ρ ⋅ π ⋅ dρ =
D 2 0
ρ
O
D
πD 4
32
=
极惯性矩的单位： 极惯性矩的单位：m4
×
d D
环形截面： 环形截面： I P
π
32
(D4 − d 4 )
同一截面，扭矩 极惯性矩I 为常量， 同一截面，扭矩T ，极惯性矩 P 为常量，因此各点切应 成正比， 力τ 的大小与该点到圆心的距离ρ 成正比，方向垂直于圆的 半径，且与扭矩的转向一致。 半径，且与扭矩的转向一致。
A
a
1
2 B 3
b
b
4
a
C
16T1 T1 = τ1 = WP1 π D 3 16 ×1000 = π × 53 = 40.74 MPa

杆件的基本变形形式
杆件的基本变形形式有以下几种：
1. 拉伸和压缩：当杆件受到沿其轴向的力时，杆件会发生拉伸或压缩变形。

拉伸时杆件长度增加，压缩时杆件长度减小。

2. 剪切：当杆件受到垂直于其轴向的力时，杆件会发生剪切变形。

剪切变形表现为杆件的横截面发生相对错动。

3. 扭转：当杆件受到绕其轴线的力矩时，杆件会发生扭转变形。

扭转变形使得杆件的横截面绕轴线旋转。

4. 弯曲：当杆件受到垂直于其轴线的横向力时，杆件会发生弯曲变形。

弯曲变形导致杆件的轴线发生弯曲。

这些基本变形形式是杆件在不同加载条件下的主要响应方式。

在工程和力学领域中，了解杆件的基本变形形式对于设计和分析结构非常重要。

通过对这些变形形式的研究，可以确定杆件在负载下的应力、应变分布以及可能的破坏模式。

需要注意的是，实际工程结构中的杆件可能同时受到多种变形形式的组合作用。

例如，在一个梁的设计中，可能同时存在弯曲和剪切变形。

因此，在分析杆件的变形和应力时，需要综合考虑各种变形形式的影响。

希望这些信息对你有所帮助！如果你有其他问题，请随时提问。

右图为工字形断面在自由扭转时的 剪应力分布情况
其分布规律为： 沿壁厚为线性分布，在壁厚中心线 处为零。
任意曲线形状的开口薄壁断面亦可以看作 是狭长矩 形断面组合的结果（图a），故其扭转惯性矩亦可用公式 （3-9）推广得到：
t
J 1 sl t 3ds 30
s1
式中s为沿薄壁断面中心线的坐标;s1为薄壁断面的 长度。
剪流为： 式中 A D12 / 4
t Mt D1t Mt J 2 2A
为薄壁管壁中心线所包围的面积
（3-4）
➢非圆断面的自由扭转
与圆截面自由扭转的最大区别：
①翘曲问题
如果杆件断面不是圆形，则扭转变形特征 有所不同，其主 要差别在扭转时段面不在保持 平面而发生“翘曲”(warping)
但翘曲是自由的 在自由扭转条件下，因杆扭转不受阻碍，所以各段面 的翘
在计算杆件断面在其平面内的扭转位移时可把断面当作一 刚体一样发生平面运动，断面在扭转时各组成部分的扭角相同。
，
工字形断面在扭转后的变形情况:
φ'1 φ'2 φ'3
截面的变形条件
整个工字形断面的扭矩满足力的平衡条件
Mt1 Mt2 Mt3 Mt
截面的力平衡条件
截面的力平衡条件
Mt1 Mt2 Mt3 Mt
开口薄壁断面的扭转惯性矩与壁厚的三次方成正比 例,因此壁厚的大小对扭转惯性矩的影响甚为显著，即 开口薄壁杆件的壁厚越小，其抗扭能力越小，反之薄 壁增加，抗扭能力大大增加。
：
➢闭口薄壁杆件的自由扭转
其主要特征是：
杆件在扭转时断面中的剪应力将沿着断面形成剪应力流。
用 f 表示。
• t 因为壁厚很小，故可认为剪应力沿壁厚不变，

2, 由强度条件可得: 由强度条件可得:
由刚度条件可得: 由刚度条件可得:
所以,空心轴的外径应不小于 所以,空心轴的外径应不小于147mm. .
8.5.2 杆件的刚度设计 从挠曲线的近似微分方程及其积分可以看出, 从挠曲线的近似微分方程及其积分可以看出, 弯曲变形与弯矩大小,跨度长短,支座条件, 弯曲变形与弯矩大小,跨度长短,支座条件,梁 有关. 截面的惯性矩 ,材料的弹性模量 有关.故提高 梁刚度的措施为: 梁刚度的措施为: 1) 改善结构受力形式,减小弯矩 ; 改善结构受力形式, 2) 增加支承,减小跨度 ; 增加支承, 3) 选用合适的材料,增加弹性模量 .但因各 选用合适的材料, 种钢材的弹性模量基本相同, 种钢材的弹性模量基本相同,所以为 提高梁的刚 度而采用高强度钢,效果并不显著; 度而采用高强度钢,效果并不显著; 4) 选择合理的截面形状,提高惯性矩 ,如工字形 形状,
4,由于实际无变形,所以: ,由于实际无变形,所以:
解得: 解得:
已知α=30.,杆长 杆长L=2m,直径 直径d=25mm, 【例8.3 】已知 直径 , E=210GPa,P=100kN,求节点 的位移. 求节点A的位移 , 求节点 的位移.
【解】
§8.2 圆轴的扭转变形
圆截面直杆在扭转时,小变形情况下, 圆截面直杆在扭转时,小变形情况下,可认为各 横截面之间的距离保持不变,仅绕轴线作相对转动, 横截面之间的距离保持不变 , 仅绕轴线作相对转动 , 表示. 两横截面间相对转过的角度称为 扭转角 , 用 φ表示 . 表示 取一微段dx研究,设徽段d 的相对扭转角为dφ, 取一微段 x研究,设徽段dx的相对扭转角为 ,沿 轴线方向的变化率为dφ/dx . 在线弹性范围内 , 由 轴线方向的变化率为 x 在线弹性范围内, 5-22) 式(5-22)可知 :

圆截面杆的扭转外力与内力 || 圆杆扭转切应力与强度条件 || 圆杆扭转变形与刚度条件 || 圆杆的非弹性扭转1.外力与内力杆件扭转的受力特点是在垂直于其轴线的平面内作用有力偶（图2·2-1a），其变形特点是在任意两个截面绕轴线发生相对转动。

轴类构件常有扭转变形发生。

作用在传动轴上的外力偶矩m通常是根据轴所传递的功率N和转速n(r/min)来计算。

当N的单位为千瓦（kW）时当N的单位为马力（HP）时扭转时的内力为扭矩T，用截面法求得。

画出的内力图称为扭矩图（或T图），如图2·2-1b所示图2·2-1 圆杆的扭转2.圆杆扭转切应力与强度条件当应力不超过材料的剪切比例极限r p时，某横截面上任意C点（图2·2-2）的切应力公式为式中T——C 点所在横截面上的扭矩p——C点至圆心的距离L p——横截面对圆心的极惯性矩，见表2-2-1 等直杆扭转时的截面几何性质。

图2·2-2 切应力分布圆杆横截面上的切应力r沿半径呈线性分布，其方向垂直于半径（图2·3-2）。

模截面上的最大切应力在圆周各点上，其计算公式为等截面杆的最大切应力发生在T max截面（危险截面）的圆周各点（危险点）上。

其强度条件为式中，[τ]为许用扭转切应力，与许用拉应力[σ]的关系为：[τ]=（0.5～0.6）[σ] (塑性材料)或[τ]=（0.5～0.6）[σ]（脆性材料）3.圆杆扭转变形与刚度条件在比弹性范围内，圆杆在扭矩T作用下，相中为L的两截面间相对扭转角为或式中G——材料的切变模量单位扭转角公式为或式中GL p——抗扭刚度圆杆上与杆轴距离为p外（图2·2-2）的切应变r为圆杆表面处的最大切应变为式中,r——圆杆的半径等截面圆杆的最大单位扭转角，发生在T max一段内，其刚度条件为式中,[θ]为圆杆的许用单位扭转角（°）/m4.圆杆的非弹性扭转讨论圆杆扭转时切应力超过材料的比例极限并进入塑性状态的情况。

200 kW。试做轴力图。
(a)
P2
P3
P1
n
P4
B
C
D
A
例题3-2图
m P2 2
m P3 3
P1
m1
m n
4 P4
B
C
D
A
m2
m3
m1
m4
(b)
B
C
A
D
解:1.计算外力偶矩
m1
m2
9.55 P1 15.9kN .m
m3
n
9.55
P2
n
4.78kN
.m
m4
9.55 P4 n
6.37kN .m
2.由计算简图用截面法计算各段轴内的扭矩，然后画扭矩图
§3.1 扭转的概念和实例
➢ 扭转变形 ——作用在垂直于杆件轴线的平面内 的力偶矩，使得杆件的任意两个 横截面都发生了绕轴线的相对转 动。
➢ 扭转变形杆件的内力 ——扭矩（T ）
➢ 轴 ——主要承受扭矩的构件
m A'
g
A
m B j B'
扭转的受力特征 ：在杆件的两端作用两个大小相等、
转向相反、且作用平面垂直于杆件轴线的力偶。
dA
O r
dA
dA
O
A
G 2
dj
dx
dA
G
dj
dx
A
2dA
T
GI p
dj
dx
令 Ip A 2dA
dj
dx
T GI p
代入物理关系式
G
dj
dx
得：
T
Ip
T
Ip
—横截面上距圆心为处任一点剪应力计算公式。

第四章 扭转4.1预备知识一、基本概念 1、扭转变形扭转变形是杆件的基本变形之一，扭转变形的受力特点是：杆件受力偶系的作用，这些力偶的作用面都垂直于杆轴。

此时，截面B 相对于截面A 转了一个角度ϕ，称为扭转角。

同时，杆件表面的纵向直线也转了一个角度γ变为螺旋线，γ称为剪切角。

2、外力偶杆件所受外力偶的大小一般不是直接给出时，应经过适当的换算。

若己知轴传递的功率P(kW)和转速n(r/min)，则轴所受的外力偶矩)(9549Nm nPT =。

3、扭矩和扭矩图圆轴扭转时，截面上的内力矩称为扭矩，用T 表示。

扭矩的正负号，按右手螺旋法则判定。

如扭矩矢量与截面外向法线一致，为正扭矩，反之为负；求扭矩时仍采用截面法。

扭矩图是扭矩沿轴线变化图形，与轴力图的画法是相似4、纯剪切 切应力互等定理单元体的左右两个侧面上只有切应力而无正应力，此种单元体发生的变形称为纯剪切。

在相互垂直的两个平面上，切应力必然成对存在且数值相等，两者都垂直于两个平面的交线、方向到共同指向或共同背离积这一交线，这就是切应力互等定理。

5、切应变 剪切虎克定律 对于纯剪切的单元体，其变形是相对两侧面发生的微小错动，以γ来度量错动变形程度，即称切应变。

当切应力不超过材料的剪切比例极限时，切应力τ和切应变γ成正比，即τ=G γG 称材料的剪切弹性模量，常用单位是GPa 。

6、圆杆扭转时的应力和强度计算(1) 圆杆扭转时，横截面上的切应力垂直于半径，并沿半径线性分布，距圆心为ρ处的切应力为ρτρpI T =图式中T 为横截面的扭矩，I p 为截面的极惯性矩。

(2) 圆形截面极惯性矩和抗扭截面系数实心圆截面324D I p π=， 163D W p π=（D 为直径） 空心圆截面)1(3244a D I p -=π， )1(1643απ-=D W p （D 为外径，d 为内径，D d /=α）(3)圆杆扭转时横截面上的最大切应力发生在外表面处tW T =max τ 式中W t =I p /R ，称为圆杆抗扭截面系数（或抗抟截面模量）。

其中 2 d A A
称为横截面的极惯性矩Ip，
它是横截面的几何性质。
以Ip
2 d A 代入上式得：
A
dj T
d x GI p
从而得等直圆杆在线弹性范围内扭转时，横截面上任一点
处切应力计算公式
t
ρ
G
T GIp
T
Ip
30
T
t max
d T
t max
D
t max
t
T
Ip
横截面周边上各点处 r)的
由 t d A r T 根据应力分布可知 Me A
tr0
d A T，于是有
A
t dA
t
r0
T d
A
A
T
r0 (2πr0 )
T
2πr02
引进 A0 πr02 ，上式亦可写作
t T 2 A0
m r0
x m
20
§8-4 切应力互等定理和剪切胡克定律 1. 单元体·切应力互等定理
以横截面、径向截面以及与表面平行的面(切向 截面)从受扭的薄壁圆筒或等直圆杆内任一点处截取 一微小的正六面体——单元体。
{M
e }Nm
2π
{n} r m in 60
103
因此，在已知传动轴的转速n(亦即传动轴上
每个轮的转速)和主动轮或从动轮所传递的功率P
之后，即可由下式计算作用于每一轮上的外力偶
矩： 6
{Me }Nm
9.55 103
{P}kw {n}r
Nm
min
{Me }Nm
9.55 {P}kw {n}r
kN m
kN
m
M2
M3
(9.55 150) 300

理论力学中的杆件的扭转分析杆件的扭转分析是理论力学中的一个重要内容，它研究的是杆件在受到扭转力矩作用下的力学行为。

在工程领域中，杆件的扭转分析常用于设计和优化各种结构，如轴、桥梁、风力发电机等。

本文将从理论角度介绍杆件的扭转分析方法，并探讨其在工程实践中的应用。

一、杆件的扭转分析基础要进行杆件的扭转分析，首先需要了解杆件受力的基本原理。

在扭转过程中，杆件会受到作用在两端的扭转力矩。

根据牛顿第三定律，杆件会对扭转力矩产生一个等大反向的力矩。

这两个力矩构成了一个力矩对偶系统，使得杆件绕其轴线发生旋转，即发生扭转变形。

扭转分析中需要考虑的关键参数是杆件的几何形状和材料性质。

杆件的几何形状包括长度、直径等。

杆件的材料性质包括弹性模量和剪切模量等。

这些参数对于杆件的扭转刚度和强度都有很大的影响。

二、杆件的扭转分析方法1.杆件的扭转刚度分析杆件的扭转刚度是指杆件在受到一定扭转力矩作用下所发生的扭转变形与扭转力矩之间的关系。

通常情况下，杆件的扭转变形是线性的，即扭转角与扭转力矩成正比。

扭转刚度可以通过杆件的几何形状和材料性质来计算。

对于直径均匀的圆杆来说，扭转刚度可以通过公式k = G * J / L来计算，其中G为剪切模量，J为截面的极惯性矩，L为杆件的长度。

除了圆杆，其他不规则形状的杆件可以采用类似的方法进行扭转刚度分析。

2.杆件的扭转强度分析杆件的扭转强度是指杆件在受到一定扭转力矩作用下所能承受的最大力矩。

扭转强度分析是为了保证杆件的正常使用，在设计和优化结构时非常重要。

根据杆件的几何形状和材料性质，可以采用各种不同的扭转强度计算方法。

对于圆杆来说，可以采用最大剪应力理论或者最大应变能理论来计算扭转强度。

而对于其他形状的杆件，可以采用相应的杆件形式系数来修正扭转强度。

三、杆件的扭转分析应用杆件的扭转分析在工程实践中有广泛的应用。

以轴为例，轴是一种常见的传动元件，承受着旋转和扭转作用。

在设计轴时，需要考虑轴的强度和刚度，以确保轴在工作过程中不会发生过大的变形和破坏。

第八章 圆轴的扭转工程构件一般可分为三类。

第四章已指出：杆是某一方向尺寸远大于其它二方向尺寸的构件，若杆件的轴线为直线，则称为直杆。

此外，若构件在某一方向的尺寸远小于其它二方向的尺寸，称之为板。

若构件在x 、y 、z 三个方向的尺寸具有相同的数量级，则称为块体。

本课程主要讨论直杆，这是一种最简单的构件。

如同4.4节所述，在空间任意力系的作用下，杆件截面内力的最一般情况是六个分量都不为零，其变形是很复杂的。

为了简化讨论，我们将杆的基本变形分成为三类，即拉压、扭转、弯曲，如图4.3所示。

前面已经讨论了在轴向载荷作用下杆的拉伸和压缩；现在再来研究杆的另一类基本变形，即扭转问题。

§8.1扭转的概念和实例工程中承受扭转的构件是很常见的。

如图8.1所示的汽车转向轴，驾驶员操纵方向盘将力偶作用于转向轴AB 的上端，转向轴的下端B 则受到来自转向器的阻抗力偶的作用，使转向轴AB 发生扭转。

又如图8.2中的传动轴，轮C 上作用着主动力偶矩，使轴转动；轮D 输出功率，受到阻力偶矩的作用，轴CD 也将发生扭转。

以上二例都是承受扭转的构件实例。

由于工程中承受扭转的构件大多为圆截面直杆，故称之为轴。

本章亦仅限于讨论直圆轴的扭转问题。

图8.2 传动轴图8.3所示为等截面直圆轴扭转问题的示意图。

扭转问题的受力特点是：在各垂直于轴线的平面内承受力偶作用。

如在图8.3中，圆轴AB 段两端垂直于轴线的平面内，各作用有一个外力偶M 0，此二力偶的力偶矩相等而转向相反，故是满足平衡方程的。

圆轴扭转问题的变形特点是：在上述外力偶系的作用下，圆轴各横截面将绕其轴线发生相对转动；任意两横截面间相对转过的角度，称为相对扭转角，以φ表示。

图8.3中，φAB 表示截面B 相对于截面A 的扭转角。

必须指出，工程中的传动轴，除受扭转作用外，往往还伴随有弯曲、拉伸(压缩)等其它形式的变形。

这类问题属于组合变形，将在以后研究。

§8.2 扭矩与扭矩图已知轴所传递的功率、转速，可利用6.3节提供的“功率、转速与传递的扭矩之关系”来计算作用于传动轴上的外力偶矩M 0。

（2）计算各段上的扭矩
M2 4.78 1 B M2 B M2
1 1
M3 4.78
2
M1 15.9 A
3
M4 6.37
(kN.m)
C T1
2 3
D
x
M3 2 T2
1
T1 M 2 0 T1 M 2 4.78kN m
x
T2 M2 M3 0
T2 M 2 M 3 9.56kN m
例1. 传动轴如图所示，已知：转速 n = 300r/min；主动 轮功率 P1= 500kW， 从动轮功率分别为P2= 150kW， P3= 150kW， P4= 200kW。 求各段的扭矩并画出轴的 扭矩图。
M2 B
M3 C
M1 A
M4
D
解: （1）计算各传动轮所受的外力偶矩
M2 4.78 B M3 4.78 C M1 15.9 A M4 6.37
2 A
基本变形公式
I p dA ——极惯性矩
● 切应力的计算式：
d G dx
d T dx GI P
T IP


T
max
( )
r
T max Tr T T max Ip I p I p Wt r IP —— 扭转截面模量(抗扭矩） Wt
D2 d 2
空心圆截面
I p dA
A
2 2 d

D d
O
D 32

4
d4
D4
32
4
1
4
32 IP D 3 Wt 14 D / 2 16

DEPARTMENT OF ENGINEERING MECHANICS KUST第八章杆件的扭转本章介绍扭转的概念轴的扭力矩、扭矩和扭矩图切应力互等定理、剪切胡克定律圆轴扭转时的应力与变形圆轴扭转的强度条件和刚度条件§8-1 扭转的概念实例对称扳手拧紧镙帽实例传动轴汽车传动轴实例扭转的概念受力特征:外力偶作用在垂直于轴线的平面内。

变形特征:两个横截面之间绕杆轴线发生相对转动j，称为扭转角；纵向线倾斜一个角度g，称为剪切角(或称剪应变) 。

扭转的概念使杆件产生扭转变形的外力偶称为扭力偶，扭，kN.m）力偶的矩称为扭力矩。

（Me承受扭矩并通过扭转传递力的杆件称为轴。

§8-2 轴的扭力矩、扭矩及扭矩图1. 扭力矩的计算切线方向的力F 产生力偶矩M e =FR 皮带的拉力F 1和F 2产生力偶矩.若F 2>F 1则M e =(F 2-F 1)D /2皮带轮或链条作用在齿轮上的切向力产生力偶矩M e =F tR齿轮功率P (kW 或HP horsepower)标示牌显示旋转速度n (r/min)[kW]9549[N m][r /min]e P M n =×[HP]7024[N m][r /min]e P M n =×602/602e e P M n M Pn p p=Þ=由转速和功率计算扭力矩1 horsepower=0.7355 KWM eM轴受外力偶矩作用时，将在横截面上产生分布剪应力，分布剪应力对质心的合力矩也是一个力偶矩，通常称为扭矩，以T (或M x )表示。

单位kN.m 。

2. 轴的扭矩T=M e扭矩T 的正负约定:+3 扭矩图坐标(x, T)用来表示沿轴线方向的扭矩变化. x表示横截面的位置.T表示扭矩的大小.我们可以画出扭矩图。

例8-1传动轴如图所示，已知：转速n = 300r/min ; 驱动功率P 1= 500kW , 被驱动齿轮功率分别为P 2= 150kW , P 3= 150kW , P 4= 200kW . 请画出轴的扭矩图.首先计算各齿轮所受的外力偶矩.1500(9549)N m 15.9kN m300M =´×=×4200(9549)N m 6.37kN m300M =×=×解:m4.78kN m N )3001509549(32×=×==M MmkN 78.421×-=-=M T mkN 37.643×==M T mkN 56.9322×-=--=M M T画扭矩图T max= 9.56 kN·m, 位于CA段上.T max= 15.9 kN·m, 位于AD段上.1. 薄壁圆管的扭转R—平均半径t(或δ)—筒壁厚度薄壁t<<2R通常t≤R/10薄壁圆管§8-3 切应力互等定理、剪切胡克定律(1)圆周线绕轴线相对转动(2)圆周线的大小和间距不变(3)各纵线倾斜同一角度(4)矩形网格变为平行四边形变形现象：薄壁圆管的扭转近似认为管内变形与管表面变形相同C ’ABttt单元体–微小六面体微体只产生剪切变形。

已知：空心圆截面轴d=20mm，D=40mm，Mx=1kN· m 求：τ A 、τ max 、τmin
解：
110 15 M x rA A 63.66MPa 4 40 Ip 4 (1 0.5 ) 32
6
max
Mx 110 84.88MPa 3 WP 40 4 (1 0.5 ) 16
②施加一对外力偶 Me。
实验现象：
Me
Me
1.各圆周线绕轴线有相对转动，但形状、大小及相邻 两圆周线之间的距离均不变 。 这说明横截面上没有正应力 2. 在小变形下，各纵向线倾斜了同一角度，但仍为 直线，表面的小矩形变形成平行四边形。 这说明横截面上有切应力 (由于壁很薄，可以假设剪应力沿壁厚均匀分布)


m-m截面上切应力引起的 内力系对x轴的力矩：
M x 2 r r
x
M
0
Me M x 0
Me 2 2 r
二、切应力互等定理
三、切应变
剪切胡克定律
单元体截面上只有切应力而无正应力作用，这种 应力状态叫做纯剪切应力状态。 纯剪切单元体的相对两侧面将发生微小的相对错 动，使原来互相垂直的两个棱边的夹角 ( 直角 ) 改变了 一个微量γ即为切应变。
②| Mx |max值及其截面位置 （危险截面）。
强度计算

x
例8-2
MB
计算例8-1中所示轴的扭矩，并作扭矩图。 M M M 解： M A 1592N m
A C D

MB
B
C
M B M C 477.5N m
A D
M x1
M D 637N m
x
B MB MC