开口薄壁梁的扭转理论与应用_王兆强
- 格式:pdf
- 大小:462.21 KB
- 文档页数:5




薄壁截面杆件的自由扭转变形能力比较刘晓红【摘要】近些年建筑行业对薄壁杆件的应用在迅猛增加,冷弯形成的各种杆件以及焊接、热轧薄壁杆件在钢结构中比比皆是.本文进行对比研究相同材料用量下工字形、T形开口薄壁截面杆和圆形、箱型、三角形闭口薄壁截面杆在自由扭转时的变形能力,分析了相同材料用量下工字形、箱形和三角形薄壁截面杆高宽比对截面扭转变形能力的影响.【期刊名称】《四川建材》【年(卷),期】2016(042)008【总页数】3页(P55-57)【关键词】薄壁截面杆件;自由扭转;扭转变形能力;高宽比【作者】刘晓红【作者单位】宁夏建设职业技术学院,宁夏银川 750021【正文语种】中文【中图分类】U442钢结构杆件在满足强度、刚度、稳定性要求的前提下,如能选择最佳截面来减少钢材损耗量、降低造价,将带来良好的经济效益和社会效益。
而薄壁结构杆件恰好具有重量轻、强度大、能充分利用材料的特点,所以各发达国家先后制定了关于薄壁结构的设计规范,我国也于1969年颁布了《弯曲薄壁型钢结构技术规范(草案)》,1975年又颁布了TJ18-75《薄壁型钢结构技术规范》,1987年颁布了GBJ18-87《冷弯薄壁型钢结构技术规范》和2002年颁布的GB5008-2002《冷弯薄壁型钢结构技术规范》共计4个版本。
国家体育场“鸟巢”主结构和次结构均采用焊接扭曲薄壁箱型截面,对此我国专家首次在国内外提出复杂扭曲薄壁箱型构件的设计理论与工程构型方法,可见薄壁杆件应用前景广阔。
扭转是工程中较为常见的一种现象,对薄壁截面扭转性能的研究是在试验和理论分析的基础上发展起来的。
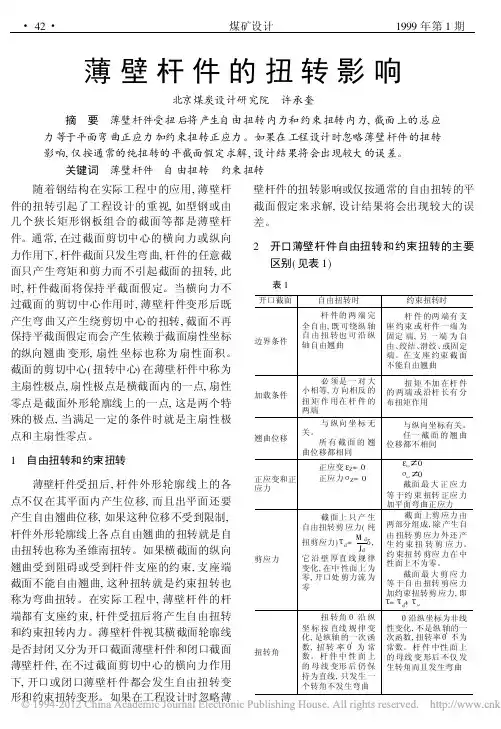
无论是开口截面还是闭合截面,根据支撑情况和加载方式的不同,扭转分为两类:自由扭转(轴向位移是自由的)和约束扭转(轴向位移受到约束)。
针对薄壁杆件自由扭转问题,鲁汉银、郭建华[1] 已经做出了相关研究,本文与其不同之处在于:①鲁汉银等的研究仅限于三种闭合截面薄壁杆件,而本文增加了两种开口截面薄壁杆件工字型截面杆[2-5]和T形截面杆的研究,五种薄壁杆件自由扭转性能形成更鲜明对比;②鲁汉银等的文章从抗扭承载力方面研究薄壁截面杆件的扭转性能,而本文从扭转变形能力方面进行研究,通过变形能力可以使薄壁截面杆件的扭转性能对比更有说服力。



第六讲 薄壁杆件的约束扭转第一节 基本假定薄壁杆件的自由扭转是指杆件受扭时,截面的纵向翘曲位移不受约束,因而纵向翘曲应变和相应的正应力都不存在。
当截面的纵向翘曲位移受到约束时,便产生约束正应力和相应的附加剪应力,这便是约束扭转。
约束扭转的分析,可以从确定截面上纵向翘曲位移着手,进而利用弹性理论的几何方程确定纵向翘曲应变;利用物理方程确定翘曲正应力;最后利用微单元的平衡方程确定相应的翘曲剪应力。
薄壁杆件的约束扭转分析中,除沿用前两章的若干基本假定(包括平面假定、线性假定、小变形假定和周边投影不变形假定)外,补充的基本假定有:1、约束扭转产生的正应力和剪应力沿壁厚均匀分布(参见图5-7),并且杆件纵向纤维不存在正应力。
据此假定,由图3-2所示薄壁单元体s z d d 在z 轴方向的平衡条件,可得到截面正应力和剪应力间的微分关系,即式(3-19)0=∂∂+∂∂zt s q σ(6-1)(3-19) 2、在约束扭转分析中,杆件纵向翘曲位移w 采用自由扭转时的表达式。
根据弹性理论,参照图6-1,薄壁单元体s z d d 的剪切应变为:=γzs w ∂∂+∂∂ξ(6-2)由周边投影不变形假定有:ρφξ=。
这里,φ为扭转角,ρ为扭转中心S 到点P 切线的垂直距离c ρ(见图3-4),于是式(6-2)可写为:=γ+∂∂swφρ' 那么,纵向翘曲位移的一般表达式便可由此积分求得,即⎰⎰+'-=ssw s s w 0d d ρφγ (6-3)式中0w 为s =0处的翘曲位移值。
0)≠γa图6-10)=γb参照第三讲剪力中心推导中关于扇性坐标的定义有:⎰=s s dρω(6-4)(3-30-1)式中ω为自积分起点至扇性零点(s=0,)0=ω到s点所包围的扇性面积的2倍。
于是,纵向翘曲位移的一般表达式(6-3)可写为:d wsw s⎰+'-=ωφγ(6-5)对于开口薄壁杆件,其在中面上的自由扭转剪应变0=中γ,代入上式便得截面的纵向翘曲位移表达式/ww+-=ωφ(6-6)对于闭口薄壁杆件,其在中面上的自由扭转剪应变0≠中γ,根据虎克定律Gτγ=,分别按单室或多室闭口截面确定剪应力τ剪应变γ。



在偏心荷载作用下薄壁箱梁剪力滞效应和约束扭转梁段有限元分析王小鹏【摘要】选取剪力滞引起的附加挠度作为广义位移,应用初参数法分别求得箱梁剪力滞弯曲变形单元刚度矩阵和约束扭转刚度矩阵,提出一种剪力滞弯扭箱梁单元,适合分析纵向弯曲、剪力滞和约束扭转之间的耦合关系,并对一有机玻璃简支箱梁模型进行计算,所得的跨中截面应力值与AN-SYS计算所得应力值基本吻合,验证了该单元的可靠性.经过对该模型内力分析可得:纵向弯曲弯矩图和剪力滞广义力矩图线形的走势基本相同,但在数值上纵向弯曲弯矩值的绝对值恒大于剪力滞广义力矩值的绝对值,在集中荷载作用处两者相差最大;扭翘双力矩的峰值出现在集中荷载作用位置处,且峰值有快速衰减的局部特征.【期刊名称】《兰州工业学院学报》【年(卷),期】2016(023)001【总页数】5页(P44-48)【关键词】剪力滞效应;约束扭转;初参数;附加挠度;有限元法【作者】王小鹏【作者单位】兰州交通大学土木工程学院,甘肃兰州730070【正文语种】中文【中图分类】U448.213薄壁箱形梁具有良好的结构性能,在现代各种桥梁中广泛使用[1].在偏心荷载作用下,箱形梁总是处于弯扭耦合的复杂受力状态[2-3].与板壳有限元相比,梁段有限元法分析箱形梁的剪力滞和约束扭转具有输入数据少,节点自由度少,输出结果便于设计人员直接使用等优点,因而被众多学者应用[4-8].在分析箱梁剪力滞效应时,上述文献都是以翼缘板的最大剪切转角差或最大纵向位移差作为广义位移[9-10],这样的广义位移没有明显的物理意义,而文献[11]中以剪力滞引起的附加挠度作为广义位移,将箱形梁的剪力滞变形从初等梁挠曲变形状态中分离出来,作为一种独立的基本变形状态.因此,在任意外荷载作用下薄壁箱梁有纵向弯曲、横向弯曲、剪力滞、畸变和刚性扭转[12]5种基本变形状态.文章以剪力滞引起的附加挠度作为广义位移,分析箱梁剪力滞效应,提出一种适合分析纵向弯曲、剪力滞和刚性扭转的梁段有限元法.结合一个简支箱梁模型,具体分析在偏心荷载作用下横截面内力分布的情况.如图1所示,箱梁发生挠曲变形时,横截面上任一点处的纵向位移可表示为式中,w(z)为相应初等梁的挠度;f(x)为剪力滞效应引起的附加挠度;wζ(x,y)为剪力滞翘曲位移函数;w(x,y)为相应于附加挠曲转角-f'(z)的剪力滞广义翘曲位移函数,即(x,y).η为考虑剪力滞翘曲应力自平衡条件的修正系数,即.其中,Ix=∫Ay2dA;Iyζ=∫AyωζdA.Ix为初等梁理论中对水平形心轴的惯性矩,Iyζ为剪力滞翘曲惯性积.选取箱梁翼缘板的剪力滞翘曲位移函数为二次抛物线ωζ=其中,;A为箱梁横截面面积;At,Ac,Ab分别为箱梁顶板,两侧悬臂版,底板的截面积,其他符号意义见图1(b)所示.箱梁的总势能Π可表达为式中,G和E分别为剪切弹性模量和杨氏弹性模量;2dA.总势能Π求其一阶变分δΠ,根据最小势能原理得剪力滞控制微分方程为故与初等梁的挠度w和挠曲转角-w'相应的内力分别为剪力-EIxw″'和弯矩-EIxw″.与剪力滞效应引起的附加挠度f相应的广义内力为剪力滞广义剪力Qω,即Qω=η2GAζf'-EIωf″',与剪力滞附加挠曲转角-f'相应的广义内力为剪力滞广义力矩wω,即wω=-EIωf″.令p=0,求解方程(5)得式中,C1~C4为积分常数;k为Reissner参数,.如图2所示,箱梁在外荷载作用下发生扭转,横截面上任一点的纵向翘曲位移可表达为式中,(s)为闭口截面广义主扇形坐标;β(z)为扭翘广义位移.β'(z)表示截面的翘曲程度,它与扭转角φ(z)有一定的关系式中,μ为截面约束系数,;Jρ为截面的极惯性矩,Jρ=∮ρ2tds,ρ为扭转中心到截面中线的垂直距离;Jd为截面的扭转惯矩,;Ω为截面中周线所围面积的两倍. 箱梁约束扭转微分方程为关于β的微分方程:关于φ的微分方程:式中,G和E分别为剪切弹性模量和杨氏弹性模量;为广义主扇形惯矩,2tds.故扭转角φ和扭翘广义位移β相应的内力为扭矩T和扭翘双力矩B.令m=0,求解方程(10)得式中:C1~C4为积分常数;k2为约束扭转的弯扭特性系数,.如图3所示,提出一种剪力滞弯扭箱梁单元,适合分析纵向弯曲,剪力滞和约束扭转之间的耦合关系,箱梁单元具有12个自由度,单元节点位移列向量为,.式中,wi和wj分别为单元i端和j端初等梁的挠度;αi和αj分别为i端和j端的初等梁的挠曲转角;fi和fj分别为i端和j端的剪力滞附加挠度;θi和θj分别为i端和j端的附加挠度转角;φi和φj分别为i端和j端的扭转角;βi和βj分别为i端和j端的扭翘广义位移.与单元节点位移列向量对应的单元节点力列向量为,.式中,Qi和Qj分别为单元i端和j端初等梁的剪力;Mi和Mj分别为i端和j端的初等梁的弯矩;Qwi和Qwj分别为i端和j端的剪力滞广义剪力;Mwi和Mwj分别为i端和j端的广义力矩;Ti和Tj分别为i端和j端的扭矩;Bi和Bj分别为i端和j端的扭翘双力矩.轴线处节点位移和节点力之间的关系可写成如下矩阵形式:其中,K为联系梁轴处节点力与节点位移的单元刚度矩阵.单元刚度矩阵K中与纵向弯曲有关的各元素可从相关的一本关于杆系结构有限元的书中引用,与单元两端剪力滞附加挠度和附加挠度转角有关的元素可参见文献[6].与单元两端的扭转角和扭翘广义位移有关的元素可参见文献[8].必须注意的是单元刚度矩阵K中各元素的位置顺序应与式(12)中的位置顺序保持一致.在求解总刚度方程之前,应先组集总荷载列向量.然后求解方程可得节点位移δ和作用在梁轴的单元节点力列向量F,即F=Kδ.用Fortran语言,按照文章建立的单元刚度矩阵编制简支箱梁剪力滞弯扭效应分析的有限元电算程序MFrame2,利用该程序对一有机玻璃单室箱梁模型进行计算,该模型为简支梁,该梁总长1.6m,材料弹性模量为3.3GPa,泊松比为0.375,如图4所示.当竖向集中荷载P=980N作用在跨中截面梁顶边腹板位置时,作出此工况下箱梁的挠度变形图,纵向弯曲弯矩和剪力滞广义力矩图,扭翘双力矩图,如5~7所示. 为了验证文章梁段单元的可靠性,用ANSYS中的SHELL63壳单元对模型进行模拟计算,计算出跨中横截面处的应力如图8~9所示.从图8和图9可知,应用剪力滞弯扭箱梁单元求出的应力值和按照ANSYS有限元软件中SHELL63壳单元算出的应力值总体吻合,故文章梁单元是合理的,适合分析纵向弯曲,剪力滞变形和约束扭转之间的耦合关系.简支箱梁截面上的正应力由纵向弯曲正应力,剪力滞正应力,约束扭转正应力叠加而成.从图5可得剪力滞变形作为一种基本的变形,在跨中引起的附件挠度最大.由图6所示,可得在同一截面上纵向弯曲弯矩恒大于剪力滞广义力矩,两者在荷载作用位置附近相差最大,但两个力矩图的线性走势基本相同.从图7可得扭翘双力矩的峰值出现在集中荷载作用位置处,且峰值有快速衰减的局部特征.文章以附加挠度作为剪力滞广义位移,考虑约束扭转,提出了一种剪力滞弯扭箱梁单元,计算得到了单元刚度矩阵.用Fortran语言编制了相应程序,并与ANSYS壳单元解相比较,验证了该单元的可靠性.适合分析纵向弯曲,剪力滞变形和约束扭转之间的耦合关系.简支箱梁截面上的正应力由纵向弯曲正应力,剪力滞正应力,约束扭转正应力叠加而成.通过对有机玻璃简支箱梁模型计算,当集中荷载作用于跨中腹板顶处时,在跨中引起的附加挠度最大,纵向弯曲弯矩图与剪力滞广义力矩图线形走势基本相同,但在数值上纵向弯曲弯矩值的绝对值恒大于剪力滞广义力矩值的绝对值;在集中荷载作用处两者相差最大.扭翘双力矩的峰值出现在集中荷载作用位置处,且峰值有快速衰减的局部特征.【相关文献】[1] 郭金琼.箱形梁设计理论[M].北京:人民交通出版社,1991.[2] 张元海,徐若昌.不规则支承条件下薄壁箱形梁的一维有限元分析[J].兰州铁道学报,1994(2):22-28.[3] 张元海,李乔.斜交箱梁桥剪滞效应的有限元分析[J].西南交通大学学报,2005,40(1):64-68.[4] 谢旭,黄剑源.薄壁箱梁桥约束扭转下翘曲、畸变和剪力滞效应的空间分析[J].土木工程学报,1995(4):31-34.[5] 罗旗帜,吴幼明,刘光栋.变高度薄壁箱梁的剪力滞[J].铁道学报,2003,25(5):81-87.[6]LuoQZ,WuYM,LiQS,etal.Afinitesegmentmodelforshearlaganalysis[J].EngineeringStructures, 2004, 26(14):2113-2124.[7] ZhouS.Finitebeamelementconsideringshear-lageffectinboxgirder[J].JournalofEngineeringMechanics, 2010, 136(9):1115-1122.[8] ZhangY.Improvedfinite-segmentmethodforanalyzingshearlageffectinthin-walledboxgirder[J].JournalofStructuralEngineering, 2011, 138(10):1279-1284.[9] 韦成龙,曾庆元,刘小燕.薄壁曲线箱梁桥剪滞效应分析的一维有限单元法[J].中国公路学报,2000,13(l):65-72.[10] 罗旗帜.薄壁箱形梁剪力滞计算的梁段有限元法[J].湖南大学学报,1991,18(2):33-38.[11] 张元海,李琳,林丽霞,等.以附加挠度作为广义位移时薄壁箱梁剪力滞效应的梁段有限元分析[J].土木工程学报,2013(10):100-107.[12] 张元海.薄壁箱梁的挠曲扭转有限元分析[J].土木工程学报,1995(6):28-36.。
薄壁梁变形分析的基本理论薄壁梁变形分析的基本理论1. 引言薄壁梁是一种在工程结构中常见的构件,其具有体积轻、成本低、易加工等优点,被广泛应用于航空、航天、汽车、建筑等领域。
为了确保薄壁梁在使用过程中的安全可靠,需要对其变形特性进行分析和计算。
本文将介绍薄壁梁变形分析的基本理论。
2. 薄壁梁的基本假设薄壁梁是指其截面形状相比于其长度来说非常细长的梁。
在薄壁梁变形分析中,通常采用以下基本假设:(1) 梁截面平面仍保持平面;(2) 梁截面内各点之间的距离不变;(3) 材料力学性质在整个截面中是均匀的;(4) 剪切变形可以忽略。
3. 梁的变形与应变在考虑以上基本假设的情况下,薄壁梁的变形与应变可以通过一系列公式来描述。
其中最常用的是梁的切线方程、挠曲方程和剪切方程。
(1) 切线方程:切线方程描述了梁上任意一点剪力和弯矩之间的关系。
根据切线方程,可以计算出梁在不同位置的弯矩分布情况。
(2) 挠曲方程:挠曲方程描述了梁的挠曲变形情况。
通过挠曲方程,可以计算出梁的挠度分布情况,进而推导出梁的位移和变形。
(3) 剪切方程:剪切方程描述了梁在剪力作用下的变形情况。
通过剪切方程,可以计算出梁在不同位置的剪应变和剪应力。
4. 薄壁梁的应力分析在薄壁梁的变形分析中,计算其应变分布并不足以确定其受力状态。
因此,需要对薄壁梁的应力进行分析。
(1) 弯曲应力:薄壁梁受弯曲作用时,其截面上会产生弯曲应力。
根据材料的弹性力学性质,可以通过弯曲应力计算出梁的弯矩分布。
(2) 剪切应力:薄壁梁在受剪力作用下会产生剪切应力。
根据材料的剪切力学性质,可以通过剪切应力计算出梁的剪力分布。
(3) 拉应力:薄壁梁在受拉力作用下会产生拉应力。
根据材料的拉伸力学性质,可以通过拉应力计算出梁的拉力分布。
5. 薄壁梁的稳定性分析薄壁梁在受外力作用下可能会发生稳定性失效,因此需要进行稳定性分析。
(1) 屈曲分析:屈曲是指薄壁梁在受外力作用下产生的稳定性失效。