信号与系统习题集18359
- 格式:doc
- 大小:1.43 MB
- 文档页数:30

选择练习题一1.卷积积分)(*2t e t δ'-等于: ( D ) A. )(t δ' B.-2)(t δ' C. t e 2- D. -2t e 2-2.周期信号是( A )A.功率信号B.能量信号C.既是功率信号又是能量信号D. 二者均不是计算⎰∞∞-=-dt t t )6(sin 2πδ( D ) A .1 B .1/6C .1/8D .1/43. 不属于周期信号频谱特性的是( D ) A. 离散性 B. 谐波性 C. 收敛性 D. 连续性4.已知信号()t f 的波形如图所示,则 ()t f 的表达式( B ) A.()t t ε B.()()11--t t ε C.()1-t t ε D.()()112--t t ε 5.已知系统微分方程为dy t dty t f t ()()()+=2,若y f t t t (),()sin ()012+==ε,解得全响应为y t e t t ()sin()=+-︒-54242452,t ≥0。
全响应中24245sin()t -︒为( D ) A .零输入响应分量B .零状态响应分量C .自由响应分量D .稳态响应分量信号()f t 波形如下图a 所示,则图b 的表达式是( C )。
f(t)t024y(t)t682图a 图b(A )(4)f t - (B )(3)f t -+ (C )(4)f t -+ (D )(4)f t -6. 系统结构框图如图示,该系统的单位冲激响应h(t)满足的方程式为( C )A .dy t dt y t x t ()()()+= B .h t x t y t ()()()=- C .dh t dth t t ()()()+=δ D .h t t y t ()()()=-δ7.信号f t f t 12(),()波形如图所示,设f t f t f t ()()*()=12,则f()0为( B ) A .1 B .2 C .3D .48.若矩形脉冲信号的宽度加宽,则它的频谱带宽( B ) A .不变 B .变窄C .变宽D .与脉冲宽度无关9. 已知信号)(t f 的傅里叶变换)()()(00ωωεωωεω--+=j F 则)(t f 为( A )A.)(00t S a ωπωB. )2(00t S a ωπωC. )(200t S a ωωD. )2(200t S a ωω 9.()()()()t e t f t e t f t t εε4221,--==则()()=*t f t f 21( D )A . ()t e t ε2-B .()t e tε4-C .()()t e e t t ε4221--+ D .()()t e e t t ε4221---10. 已知一线性时不变系统,当输入)()()(3t e e t x t t ε--+=时,其零状态响应是)()22()(4t e e t y t t ε---=,则该系统的频率响应为( A )A.)521524(2++-++ωωωωj j j j B. )521524(2+++++ωωωωj j j j C. )521524(++-++ωωωωj j j jD. )521524(+++++ωωωωj j j j11..已知信号f t ()如图所示,则其傅里叶变换为( C )A .τωττωτ2422Sa Sa ()()+ B .τωττωτSa Sa ()()422+C .τωττωτ242Sa Sa ()()+D .τωττωτSa Sa ()()42+12.已知f(t)↔F(j ω),则信号y(t)=f(t)δ(t-3)的频谱 Y(j ω)=( ) A.f(3)e -j 3ω B. F(j ω)e -j 3ω C. f(3) D. F(j ω)13..周期信号f(t)=-f(t 2T±),(T —周期),则其傅里叶级数展开式的结构特点是( A ) A.只有正弦项 B.只有余弦项 C.只含偶次谐波D.只含奇次谐波14.信号)}2()2({-+--t u t u dtd的傅立叶变换是( C ) A ω2sin 2j B )(2ωπδ C -2j ω2sin D15.f(t)的频宽是200Hz,那么f(-2t-6)的奈奎斯特频率为( C )。

信号与系统题目部分,(卷面共有200题,0。
0分,各大题标有题量和总分) 一、选择题(7小题,共0.0分)[1]题图中,若h '(0)=1,且该系统为稳定的因果系统,则该系统的冲激响应()h t 为。
A 、231()(3)()5tt h t e e t ε-=+- B 、32()()()tt h t e e t ε--=+C 、3232()()55tt e t e t εε--+D 、3232()()55tt e t e t εε--+-[2]已知信号x [n]如下图所示,则x [n]的偶分量[]e x n 是。
[3]波形如图示,通过一截止角频率为50rad sπ,通带内传输值为1,相移为零的理想低通滤波器,则输出的频率分量为() A 、012cos 20cos 40C C t C t ππ++ B 、012sin 20sin 40C C t C t ππ++ C 、01cos 20C C t π+ D 、01sin 20C C t π+[4]已知周期性冲激序列()()T k t t kT δδ+∞=-∞=-∑的傅里叶变换为()δωΩΩ,其中2TπΩ=;又知111()2(),()()2T T f t t f t f t f t δ⎛⎫==++⎪⎝⎭;则()f t 的傅里叶变换为________。
A 、2()δωΩΩ B 、24()δωΩΩ C 、2()δωΩΩ D 、22()δωΩΩ[5]某线性时不变离散时间系统的单位函数响应为()3(1)2()kkh k k k εε-=--+,则该系统是________系统。
A 、因果稳定B 、因果不稳定C 、非因果稳定D 、非因果不稳定 [6]一线性系统的零输入响应为(23kk --+)u(k), 零状态响应为(1)2()k k u k -+,则该系统的阶数A 、肯定是二阶B 、肯定是三阶C 、至少是二阶D 、至少是三阶 [7]已知某系统的冲激响应如图所示则当系统的阶跃响应为。

《信号与系统》课程习题集一、计算题1. 已知一连续时间LTI 系统,输入为()(2)n f t t n δ+∞=-∞=-∑,单位冲激响应sin 3()t th t π=。
(1)求()f t 的傅里叶级数系数k a ,以及傅里叶变换()F j ω。
(2)求该系统的频率响应)(ωj H ,并概略画出其波形。
(3)求该系统输出)(t y ,以及)(ωj Y 。
2. 已知一连续时间理想高通滤波器S ,其频率响应是1,400()0,H j otherωω⎧≥⎪=⎨⎪⎩。
当该滤波器的输入是一个基波周期4T π=且傅里叶级数系数为k a 的信号()f t 时,发现有()()()Sf t y t f t −−→=。
问对于什么样的k 值,才能保证0=k a ?3. 已知一连续时间理想低通滤波器S ,其频率响应是1,200()0,>200H j ωωω⎧≤⎪=⎨⎪⎩。
当该滤波器的输入是一个基波周期8T π=且傅里叶级数系数为k a 的信号()f t 时,发现有()()()Sf t y t f t −−→=。
问对于什么样的k 值,才能保证0=k a ?4. 已知一连续时间LTI 系统,输入为()(),4n f t t nT T δ+∞=-∞=-=∑,单位冲激响应sin 2()tth t π=。
(1)求()f t 的傅里叶级数系数k a ,以及傅里叶变换()F j ω。
(2)求该系统的频率响应)(ωj H ,并概略画出其波形。
(3)求该系统输出)(t y ,以及)(ωj Y 。
5. 已知一连续时间LTI 系统,单位冲激响应sin ()t th t ππ=,输入()f t 为如图所示周期性方波。
(1)求()f t 的傅里叶级数系数k a 。
(2)求该系统的频率响应)(ωj H ,并概略画出其波形。
(3)求该系统输出)(t y ,以及)(ωj Y 。
6. 已知常系数线性微分方程描述的连续时间因果线性时不变系统。

信号与系统习题集(很有⽤)2011《信号与系统》习题集选择题1.图⽰电路的微分⽅程是:(A )()()()t v t v t v c c =+'2(B )()()()t v t v t v c c =+'2(C )()()()t v t v t v c c=+'(D )()()()t v t v t v c c 2=+'2.f[n](n-n 0)是 A f[n] B f (n-n 0) C (n-n 0) D (n )3下列傅⾥叶变换对中错误的是:A .1)(?δFt B .222a a eFta +ω?-C .)(1)(ωδ+ω?Ft uD .aj t u eFat+ω?-1)(4.下列拉普拉斯变换性质中错误的是A .时移特性)()(00s F e t t f st L-?-B .S域微分特性dss dF t tf LC .时域微分特性)()(s sF dtt df LD .时域卷积特性)()()()(s H s F t h t f L*5.已知信号f (t )的波形如图所⽰,则f (t )的表达式为 (A)(t +1)ε(t) (B)δ(t -1)+(t -1)ε(t) (C)(t -1)ε(t) (D)δ(t +1)+(t +1)ε(t) 6.若系统的起始状态为0,在x (t )的激励下,所得的响应为(A )强迫响应;(B )稳态响应;(C )暂态响应;(D )零状态响应。
7.理想不失真传输系统的传输函数H (jω)是(A )0j t Ke ω- (B )0tj Ke ω-(C )0t j Ke ω-[]()()c c u u ωωωω+-- (D )00j t Ke ω- (00,,,c t k ωω为常数)8.不满⾜)()(n u n 与δ之间满⾜如下关系(A )∑∞-∞=-=k k n n u )()(δ(B )∑∞=-=0)()(k k n n u δ(C ))1()()(--=n u n u n δ(D )()()(1)n u n u n δ=----9.中图所⽰的离散时间信号⽤单位阶跃信号u[n]表⽰的是 A f[n]=u[n+3]-u[n+1] B f[n]=u[n]-u[n+3](t v ππ--2)(t v R Ω1C F1)(t v cC10 () 11.图⽰电路的微分⽅程是:(A )()()()t u t u t u s c c 2=+'(B )2()()()t u t u t u s c c =+' (C )()()()t u t u t u s c c=+'2 (D )()()()t u t u t u s c c=+'12.信号f (t )变成)121(+t f 的过程为 (A) 先将f (t )的图形向左移⼀个单位,再时间上展宽1/2倍。

信号与系统习题答案(注:教材---郑君里编)习题一1-7 绘出下列各信号的波形:图a:[][]11()(2)(2)()(2)()(2)22f t t u t u t t u t u t =++-----[](1)(2)(2)2tu t u t =-+--图b:)2(2)1()()();2(4)]2()1([2)]1()([)(-+-+=-+---+--=t u t u t u t f t u t u t u t u t u t f图c :[])()()sin()(T t u t u t T E t f --=π1-12 绘出下列各时间函数的波形图,注意它们的区别: (1))]1()([--t u t u t ; (2))1(-t tu ; (3))1()]1()([-+--t u t u t u t ;)1(-tf(t)求f(-t),讨论图7(b)(c)(a)⇒ ⇒方法二:(1))()()(00t f dt t t t f -=-⎰∞∞-δ ;(2)⎰∞∞-=-)()()(00t f dt t t t f δ ;(3)1)2()2()(000==--⎰∞∞-tu dt t t u t t δ;(4)⎰∞∞-=-=--0)()2()(000t u dt t t u t t δ;(5)⎰∞∞---=++2)2()(2e dt t t e t δ;(6)2166sin6)6()sin (+=+=-+⎰∞∞-ππππδdt t t t ;(7)⎰∞∞----=--01)]()([0t j t j e dt t t t e ωωδδ ;1-15 电容C 1与C 2串联,以阶跃电压源v(t)=Eu(t)串联接入,试分别写出回路中的电流i(t)、每个电容两端电压vc 1(t)、vc 2(t)的表示式。
电路如图:2121c c c c +*=⇒电路电流)()(2121t E c c dt Ct i c δ+==)()(1)()()(1)(2112221211t u c c Ec dt t i c t v t u c c Ec dt t i c t v c c ⎰⎰+==+==1-20 判断下列系统是否为线性的、时不变的、因果的?(1)dt t de t r )()(=;(2))()()(t u t e t r = ;V C1(t) V C2(t)(3) )()](sin[)(t u t e t r = ; (4) )1()(t e t r -= ; (5) )2()(t e t r = ;(6))()(2t e t r = ;(7)⎰∞-=td e t r ττ)()( ;(8) ⎰∞-=td e t r 5)()(ττ 。

信号与系统练习题——第1-3章信号与系统练习题(第1-3章)一、选择题1、下列信号的分类方法不正确的是(A )A 、数字信号和离散信号B 、确定信号和随机信号C 、周期信号和非周期信号D 、连续信号和离散信号2、下列离散序列中,哪个不是周期序列? (D )A 、165()3cos()512f k k ππ=+ B 、2211()5cos()712f k k ππ=+ C 、33()9sin()5f k k π= D 、433()7sin()45f k k π=+ 3、下列哪一个信号是周期性的?(C )。
A 、()3cos 2sin f t t t π=+;B 、()cos()()f t t t πε=;C 、()sin()76f k k ππ=+; D 、1()cos()53f k k π=+。
4、周期信号()sin6cos9f t t t =+的周期为(D )A 、πB 、2πC 、12π D 、23π5、周期信号()sin3cos f t t t π=+的周期为(C )。
A 、πB 、2πC 、无周期D 、13π 6、以下序列中,周期为5的是(D ) A. 3()cos()58f k k π=+ B. 3()sin()58f k k π=+ C. 2()58()j k f k eπ+= D. 2()58()j k f k e ππ+=7、下列说法正确的是(D )A 、两个周期信号()x t ,()y t 的和信号()()x t y t +一定是周期信号B 、两个周期信号()x t ,()y t 的周期分别为2()()x t y t +是周期信号C 、两个周期信号()x t ,()y t 的周期分别为2和π,则信号()()x t y t +是周期信号D 、两个周期信号()x t ,()y t 的周期分别为2和3,则信号()()x t y t +是周期信号8、下列说法不正确的是(A )A 、两个连续周期信号的和一定是连续周期信号B 、两个离散周期信号的和一定是离散周期信号C 、连续信号()sin(),(,)f t t t ω=∈-∞+∞一定是周期信号D 、两个连续周期信号()x t ,()y t 的周期分别为2和3,则信号()()x t y t +是周期信号9、(52)f t -是如下运算的结果(C )A 、(2)f t -右移5B 、(2)f t -左移5C 、(2)f t -右移25 D 、(2)f t -左移25 10、将信号()f t 变换为(A )称为对信号()f t 的平移。
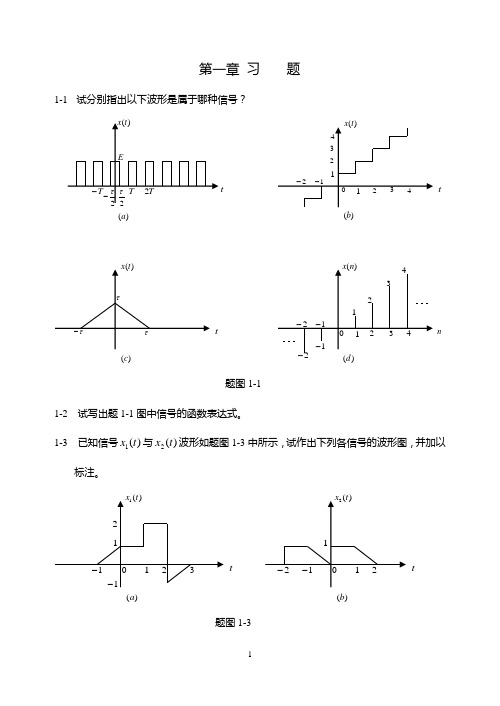
第一章 习 题1-1 试分别指出以下波形是属于哪种信号?题图1-11-2 试写出题1-1图中信号的函数表达式。
1-3 已知信号)(1t x 与)(2t x 波形如题图1-3中所示,试作出下列各信号的波形图,并加以标注。
题图1-3⑴ )2(1-t x ⑵ )1(1t x - ⑶ )22(1+t x ⑷ )3(2+t x ⑸ )22(2-t x ⑹ )21(2t x -t)(a t)(bt)(c nt)(bt)(a⑺ )(1t x )(2t x - ⑻ )1(1t x -)1(2-t x ⑼ )22(1t x -)4(2+t x1-4 已知信号)(1n x 与)(2n x 波形如题图1-4中所示,试作出下列各信号的波形图,并加以标注。
题图1-4⑴ )12(1+n x ⑵ )4(1n x - ⑶ )2(1nx⑷ )2(2n x - ⑸ )2(2+n x ⑹ )1()2(22--++n x n x ⑺)2(1+n x )21(2n x - ⑻ )1(1n x -)4(2+n x ⑼ )1(1-n x )3(2-n x 1-5 已知信号)25(t x -的波形如题图1-5所示,试作出信号)(t x 的波形图,并加以标注。
题图1-51-6 试画出下列信号的波形图:⑴ )8sin()sin()(t t t x ΩΩ= ⑵ )8sin()]sin(211[)(t t t x ΩΩ+=⑶ )8sin()]sin(1[)(t t t x ΩΩ+= ⑷ )2sin(1)(t tt x =nn)(a t1-7 试画出下列信号的波形图:⑴ )(1)(t u e t x t -+= ⑵ )]2()1([10cos )(---=-t u t u t e t x t π ⑶ )()2()(t u e t x t --= ⑷ )()()1(t u e t x t --= ⑸ )9()(2-=t u t x ⑹ )4()(2-=t t x δ1-8试求出以下复变函数的模与幅角,并画出模与幅角的波形图。

(完整版)信号与系统专题练习题及答案信号与系统专题练习题一、选择题1.设当t<3时,x(t)=0,则使)2()1(t x t x -+-=0的t 值为 C 。
A t>-2或t>-1B t=1和t=2C t>-1D t>-22.设当t<3时,x(t)=0,则使)2()1(t x t x -?-=0的t 值为 D 。
A t>2或t>-1B t=1和t=2C t>-1D t>-23.设当t<3时,x(t)=0,则使x(t/3)=0的t 值为 C 。
A t>3 B t=0 C t<9 D t=34.信号)3/4cos(3)(π+=t t x 的周期是 C 。
A π2 B π C 2/π D π/25.下列各表达式中正确的是B A. )()2(t t δδ= B.)(21)2(t t δδ= C. )(2)2(t t δδ= D. )2(21)(2t t δδ=6. 已知系统的激励e(t)与响应r(t)的关系为:)1()(t e t r -= 则该系统为 B 。
A 线性时不变系统 B 线性时变系统 C 非线性时不变系统 D 非线性时变系统7. 已知系统的激励e(t)与响应r(t)的关系为:)()(2t e t r = 则该系统为 C 。
A 线性时不变系统B 线性时变系统C 非线性时不变系统D 非线性时变系统 8. ?∞-=td ττττδ2sin )( A 。
A 2u(t) B )(4t δ C 4 D 4u(t)10.dt t t )2(2cos 33+??-δπ等于 B 。
A 0 B -1 C 2 D -211.线性时不变系统输出中的自由响应的形式由 A 决定A 系统函数极点的位置;B 激励信号的形式;C 系统起始状态;D 以上均不对。
12.若系统的起始状态为0,在x (t)的激励下,所得的响应为 D 。
A 强迫响应;B 稳态响应;C 暂态响应;D 零状态响应。

1.(P10例1.2.1)已知离散时间信号为)23cos(3)(n e t f n j ππ++=判断该信号是否为周期信号.若是确定信号的周期.2.(P15例1.3.1)已知信号波形)(t f 如图,画出)22(+t f 与)121(--t f 的波形. 3.(P20例1.4.1)求图示离散时间信号][n f 的偶部][n f e 与奇部][n f o4.(P22例1.5.1)已知离散时间信号如图所示,分别用][n δ与][n u 及其延时表示信号][n f .5.(P36例 1.7.1)已知线性时不变(LTI)离散时间系统对输入][][n n f δ=的响应为][2][n u n y =求该系统对输入]3[]1[][1--+=n u n u n f 的响应][1n y .6.(P36例1.7.2)已知连续时间系统可表示为)1()()(-=t f t f t y 问该系统是否为(1)线性系统?(2)时不变系统?(3)记忆系统?(4)因果系统?7.(P39例1.8.3)已知一个离散时间线性系统对信号n j e n f 31][=的响应为n j e n y 51][=对另一输入信号n j e n f 32][-=的响应为n j e n y 52][-=.求系统对输入信号)]1(3cos[][-=n n f 的响应][n y第一章习题(3题)1(1.4)判断下列连续时间信号是否为周期信号.如果是,求出其周期. (a) )525sin(2)(π+=t t f (b) )23()(+=t j e t f (f))cos()(2t e t f t j π+= 2(1.6)判断下列信号中,哪些是能量信号,哪些是功率信号,哪些是非能量、非功率信号. (a )tet f 2)(-=;(c )2)(=t f第一章简答题1(P30)系统的相互联接有几种?分别画出其结构图.3(1.15)画出下列信号的波形(a) ]5[][][1--=n u n u n f (b)]1[]4[][2---+-=n u n u n fn n1.(P51例2.1.1)已知一个因果LTI 离散时间系统用差分方程描述为]1[][]2[61]1[65][--=-+-+t f n f n y n y n y 且输入][][n nu n y = ,初始条件为 25]2[,21]1[=-=-y y 试求:(1)系统零输入响应][n y s (2)系统零状态响应][n y f (3)系统全响应][n y2.(P60例2.2.5)一个LTI 离散时间系统的输入信号][n f 与冲激响应为][n h 如图.分别用三种方法求系统的响应.(1)常规方法 (2)将输入信号][n f 表示为冲激信号的加权和(3)多项式相乘3.(P64例 2.3.1)已知一个因果LTI连续时间系统微分方程为)(2)()(2)(3)(////t f t f t y t y t y +=++且已知初始答件为1)0(,1)0(/==--y y 输入为)()(2t u t t f = 求系统(1)零输入响应(2)零状态响应(3)全响应4.(P71例2.4.4)已知LTI 连续时间系统的输入信号)(t f 和)(t h 冲激响应如图求系统的响应.5.(P76例2.5.1)已知LTI 系统冲激响应分别为 (1))()(t u t h =(2)]5[]1[][--+=n u n u n h 判断系统的记忆性,因果性.6.(P80例2.6.1)已知LTI 连续时间系统结构如图求整个系统的冲激响应)(t h .7.(P80例2.6.2)已知L TI离散时间系统结构如图且][)]3cos([][],2[][][],[2][21n u n n n f n n n h n u n h πδδ+=--==求系统响应.第2章习题(7题)1(2.5)己知L TI 离散时间系统输入信号 ][n f 与冲激响应][n h 如下,求系统响应][][][n h n f n y *= 并画出波形.(a)][][],[][n u n h n u n f == (e)][][],[][n u n h n u n f -==2(2.7)己知LTI 离散时间系统输入信号 ][n f 与冲激响应][n h 可用序列表示如下,用多项工方法计算卷积.(a)5,4,3};3,2,4{][;4,3,2,1};3,1,2,1{][====n n h n n f (b)5,4,3};3,2,4{][;0,1,2};1,2,1{][==--==n n h n n f3(2.10)己知因果LTI 连续时间系统的微分方程为)(2)(3)(/t f t y t y =+ 系统输入为)()32()(t u t t f -= 初始条件为1)0(=-y (1) 直接解微分方程求系统响应;(2)求系统的零输入响应与零状态响应;并验证两者之和等于系统全响应. 4(2.11)己知LTI 连续时间系统的输入输出关系如下,求各系统的冲激响应)(t h . (a))(2)(t f t y =5(2.12)己知L TI 离散时间系统输入信号 )(t f 与冲激响应)(t h 求系统响应)()()(t h t f t y *=画出响应示意图.(a))2()(),()(-==t u t h t u t f6(2.14)己知LTI 离散时间系统冲激响应][n h ,讨论系统的记忆性、因果性与稳定性。

第2章2-1 绘出下列各时间函数的波形图。
(1)1()(1)f t tu t =- (2)2()[()(1)](1)f t t u t u t u t =--+- (3)3()(1)[()(1)]f t t u t u t =---- (4)4()[(2)(3)]f t t u t u t =--- (5)5()(2)[(2)(3)]f t t u t u t =---- (6)6()()2(1)(2)f t u t u t u t =--+-解:2-5 已知()f t 波形如图题2-5所示,试画出下列信号的波形图。
t图 题2-5(3)3()(36)f t f t =+ (5)511()36f t f t ⎛⎫=-- ⎪⎝⎭解:tt2-6 已知()f t 波形如图题2-6所示,试画出下列信号的波形图。
图 题2-6(4)4()(2)(2)f t f t u t =-- (6)6()(1)[()(2)]f t f t u t u t =--- 解:2-7 计算下列各式。
(1)0()()f t t t δ+ (2)00()()d f t t t t t δ∞-∞+-⎰(3)24e (3)d t t t δ-+⎰(4)e sin (1)d t t t t δ∞-+⎰(5)d [e ()]d t t t δ-(6)0()()d f t t t tδ∞-∞-⎰(7)0()()d f t t t tδ∞-∞-⎰(8)00()d 2t t t u t t δ∞-∞⎛⎫--⎪⎝⎭⎰(9)00()(2)d t t u t t t δ∞-∞--⎰(10)(e )(2)d t t t t δ∞-∞++⎰(11)(sin )d 6t t t tδ∞-∞π⎛⎫+- ⎪⎝⎭⎰(12)j 0e [()()]d t t t t t Ωδδ∞--∞--⎰解:(1) 原式0()()f t t δ=(2)原式)2()()(0000t f dt t t t t f =-+=⎰+∞∞-δ(3)原式2334(3)e t dt e δ---=+=⎰(4)原式10sin(1)(1)0((1))e t dt t δδ+∞-=-+=+⎰不在积分区间内(5)原式)()](['0t t e dtd δδ== (6)原式)()()0(00t f dt t t f -=-=⎰+∞∞-δ(7)原式00(0)()()f t t dt f t δ+∞-∞=-=⎰(8)原式⎩⎨⎧><==--=⎰∞+∞-0100)2()2()(000000t t t u dt t t u t t δ(9)原式⎩⎨⎧<>=-=--=⎰∞+∞-0100)()2()(000000t t t u dt t t u t t δ(10)原式22(2)(2)2e t dt e δ+∞---∞=-+=-⎰(11)原式1(sin )()66662t dt ππππδ+∞-∞=+-=+⎰ (12)原式000[()()]1j t j t e t e t t dt e δδ+∞-Ω-Ω-∞=--=-⎰2-8 画出图题2-8所示各信号的偶分量和奇分量的波形。

《信号与系统》练习题1、线性性质包含两个内容: 和 。
(可加性、齐次性)2、线性时不变(LTI )连续系统的数学模型是线性常系数 方程。
(微分) 线性时不变(LTI )离散系统的数学模型是线性常系数 方程。
(差分)3、线性时不变系统具有 、 和 。
(微分特性、积分特性、频率保持性。
)4、连续系统的基本分析方法有: 分析法, 分析法和 分析法。
(时域、频域、复频域或s 域)系统依处理的信号形式,可以分为三大类:连续系统、离散系统和混合系统。
5、周期信号频谱的特点是 、 、 。
(离散性、谐波性、收敛性)6、(1)LTI 连续系统稳定的充要条件是 。
(∞<⎰∞∞-dt t h )()(2)LTI 离散系统稳定的充要条件是 。
(()∞<∑∞=0n n h ) 7、(1)已知信号()t e t f 2-=,则其频谱函数()=ωF 。
(()244ωω+=F ) (2)已知信号()()()t t e t f at εω0sin -=,则其频谱函数()=ωF 。
(()()2020ωωωω++=j a F ) 8、信号t t t f 3cos 3cos 21)(++=的傅立叶变换是 。
(()()()()[]()()[]333112++-+++-+=ωδωδπωδωδωδπωF )9、为了保证对输入信号无失真传输,系统函数必须满足的条件是 。
(()0t j Ke j H ωω-=)10、冲激信号通过理想低通滤波器后,冲激响应是 。
(()()[]0t t Sa t h c c -=ωπω) 11、为使采样信号不丢失信息,信号必须频带有限且采样间隔s T 。
(m f 21≤) 12、(1)已知()t t f --=e 2,则其单边拉式变换()=s F 。
(()()12++=s s s s F ) (2)已知()()t t t f 3e-+=δ,则其单边拉式变换()=s F 。
(()311++=s s F ) 13、(1)象函数())2)(1(4+++=s s s s s F 的逆变换 ()t f 为 。

信号与系统试题库一、选择题共50题1.下列信号的分类方法不正确的是( A ):A、数字信号和离散信号B、确定信号和随机信号C、周期信号和非周期信号D、因果信号与反因果信号2.下列说法正确的是( D ):A、两个周期信号x(t),y(t)的和x(t)+y(t)一定是周期信号。
B、两个周期信号x(t),y(t)的周期分别为2和2,则其和信号x(t)+y(t)是周期信号。
C、两个周期信号x(t),y(t)的周期分别为2和 ,其和信号x(t)+y(t)是周期信号。
D、两个周期信号x(t),y(t)的周期分别为2和3,其和信号x(t)+y(t)是周期信号. 3。
下列说法不正确的是( D ).A、一般周期信号为功率信号。
B、时限信号(仅在有限时间区间不为零的非周期信号)为能量信号。
C、ε(t)是功率信号;D、e t为能量信号;4.将信号f(t)变换为( A)称为对信号f(t)的平移或移位。
A、f(t–t0)B、f(k–k0)C、f(at)D、f (—t)5.将信号f(t)变换为(A)称为对信号f(t)的尺度变换。
A 、f (at )B 、f (t –k 0)C 、f (t –t 0)D 、f (-t )6.下列关于冲激函数性质的表达式不正确的是( B ).A 、)()0()()(t f t t f δδ=B 、()t aat δδ1)(=C 、)(d )(t tεττδ=⎰∞-D 、)()-(t t δδ=7。
下列关于冲激函数性质的表达式不正确的是(D).A 、⎰∞∞-='0d )(t t δ B 、)0(d )()(f t t t f =⎰+∞∞-δC 、)(d )(t t εττδ=⎰∞-D 、⎰∞∞-=')(d )(t t t δδ8。
下列关于冲激函数性质的表达式不正确的是( B ).A 、)()1()()1(t f t t f δδ=+B 、)0(d )()(f t t t f '='⎰∞∞-δC 、)(d )(t t εττδ=⎰∞-D 、)0(d )()(f t t t f =⎰+∞∞-δ9。

信号与系统练习及答案一、单项选择题1.已知信号f (t )的波形如题1图所示,则f (t )的表达式为( )A .tu(t)B .(t-1)u(t-1)C .tu(t-1)D .2(t-1)u(t-1)2.积分式⎰-δ+δ++4422)]dt -(t 2(t))[23(t t 的积分结果是( ) A .14 B .24 C .26 D .283.已知f(t)的波形如题3(a )图所示,则f (5-2t)的波形为( )4.周期矩形脉冲的谱线间隔与( )A .脉冲幅度有关B .脉冲宽度有关C .脉冲周期有关D .周期和脉冲宽度有关 5.若矩形脉冲信号的宽度加宽,则它的频谱带宽( ) A .不变 B .变窄 C .变宽D .与脉冲宽度无关 6.如果两个信号分别通过系统函数为H (j ω)的系统后,得到相同的响应,那么这两个信号()A .一定相同 B .一定不同 C .只能为零 D .可以不同7.f(t)=)(t u e t 的拉氏变换为F (s )=11-s ,且收敛域为( ) A .Re[s]>0B .Re[s]<0C .Re[s]>1D .Re[s]<1 8.函数⎰-∞-δ=2t dx )x ()t (f 的单边拉氏变换F (s )等于( ) A .1 B .s 1 C .e -2s D .s1e -2s 9.单边拉氏变换F (s )=22++-s e )s (的原函数f(t)等于( ) A .e -2t u(t-1) B .e -2(t-1)u(t-1) C .e -2t u(t-2)D .e -2(t-2)u(t-2)答案: BCCCBDCDA二.填空题1.如果一线性时不变系统的单位冲激响应为h(t),则该系统的阶跃响应g(t)为_________。
2.已知x(t)的傅里叶变换为X (j ω),那么x (t-t 0)的傅里叶变换为_________________。
3.如果一线性时不变系统的输入为f(t),零状态响应为y f (t )=2f (t-t 0),则该系统的单位冲激响应h(t)为_________________。

信号与系统题库(完整版)信号与系统题目部分,(卷面共有200题,0.0分,各大题标有题量和总分)一、选择题(7小题,共0.0分)[1]题图中,若h '(0)=1,且该系统为稳定的因果系统,则该系统的冲激响应()h t 为。
A 、231()(3)()5tt h t ee t ε-=+-B 、32()()()t th t ee t ε--=+C 、3232()()55tte t e t εε--+D 、3232()()55ttet e t εε--+-[2]已知信号x[n]如下图所示,则x[n]的偶分量[]e x n 是。
[3]波形如图示,通过一截止角频率为50rad s π,通带内传输值为1,相移为零的理想低通滤波器,则输出的频率分量为() A 、012cos 20cos 40C C t C t ππ++B 、012sin 20sin 40CC t C t ππ++C 、01cos 20C C t π+ D 、01sin 20CC tπ+[4]已知周期性冲激序列()()Tk t t kT δδ+∞=-∞=-∑的傅里叶变换为()δωΩΩ,其中2TπΩ=;又知111()2(),()()2T T f t t f t f t f t δ⎛⎫==++ ⎪⎝⎭;则()f t 的傅里叶变换为________。
A 、2()δωΩΩ B 、24()δωΩΩ C 、2()δωΩΩD 、22()δωΩΩ[5]某线性时不变离散时间系统的单位函数响应为()3(1)2()kkh k k k εε-=--+,则该系统是________系统。
A 、因果稳定B 、因果不稳定C 、非因果稳定D 、非因果不稳定 [6]一线性系统的零输入响应为(23kk--+)u(k), 零状态响应为(1)2()kk u k -+,则该系统的阶数A 、肯定是二阶B 、肯定是三阶C 、至少是二阶D 、至少是三阶[7]已知某系统的冲激响应如图所示则当系统的阶跃响应为。

12.连续信号与的乘积,即( ).)(t f )(0t t -δ=-)()(0t t t f δA. B. C.D. )()(00t t t f -δ)(0t t f -)(t δ)()(0t t f δ13.已知系统响应与激励的关系为()()y t ()f t 则该系统是( )系统。
2(51)()()5()[()]t y t ty t y t f t '''-++=A. 线性非时变B. 非线性非时变C. 线性时变D. 非线性时变14. 下列系统那个是因果、线性、时不变的连续系统( )。
A .B. )()(2)(3)(t f t y t y t y '=+'+'')()()(3)(t f t f t y t y ='+''C .D .)()()(3)(t f t ty t y t y =+'+'')(2)1(3)(t f t y t y =+-'+''15.若对连续时间信号进行频域分析,则需对该信号进行( ).A. LTB. FTC. Z 变换D. 希尔伯特变换16.的频谱函数为())()52(t e t j ε+-A. B. C. D. ωj e j 521-ωj e j 521+j )5(21ω++j)5(21ω++-17.若收敛坐标落于原点,S 平面有半平面为收敛区,则() A. 该信号是有始有终信号B. 该信号是按指数规律增长的信号C. 该信号是按指数规律衰减的信号D. 该信号的幅 度既不增长也不衰减而等于稳定值,或随时间成比例增长的信号n t t ,18. ,则根据终值定理有( ))22(3)(2+++=s s s s s F =∞)(f A. 0 B. 1.5 C. 0 D. 1∞19.信号与冲激函数之积为( ))2(4sin 3)2(4cos 2)(++-=t t t f ππ)2(-t δA 、2B 、2C 、3D 、5)2(-t δ)2(-t δ)2(-t δ,则该系统是()>-系统的系统函数.已知2]Re[,651)(LTI 202s s s s s H +++=A 、因果不稳定系统B 、非因果稳定系统C 、因果稳定系统D 、非因果不稳定系统21 设连续时间线性系统的单位冲激响应为h(t),系统的频率特性为,信号通)()()(ωϕωωj e j H j H =过线性系统不失真的条件是()A. 可以为任意函数,)(ωj H 0)(t ωωϕ-=B. 和都可以为任意函数)(ωj H )(ωϕC. h(t)为常数D. 为常数,)(ωj H 0)(t ωωϕ-=22. 系统的幅频特性|H (ω)|和相频特性如图2(a)(b)所示,则下列信号通过该系统时,不产生失真的是 ( )。
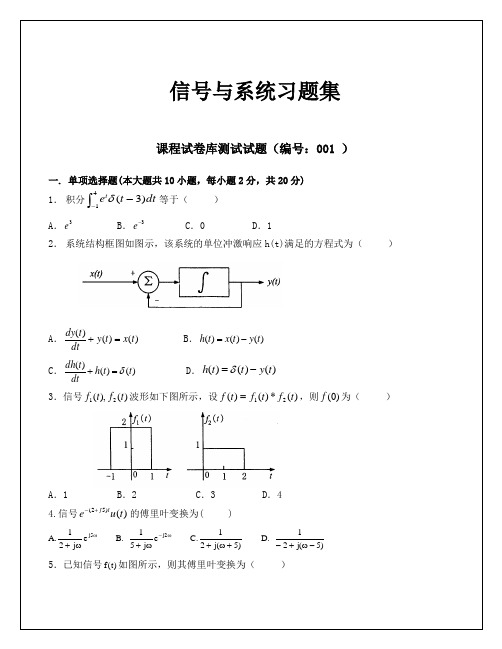
信号与系统习题集课程试卷库测试试题(编号:001 )一. 单项选择题(本大题共10小题,每小题2分,共20分) 1. 积分⎰--41)3(dt t e t δ等于( )A .3eB .3-eC .0D .12. 系统结构框图如图示,该系统的单位冲激响应h(t)满足的方程式为( )A .)()()(t x t y dtt dy =+ B .)()()(t y t x t h -=C .)()()(t t h dtt dh δ=+ D .)()()(t y t t h -=δ 3.信号)(),(21t f t f 波形如下图所示,设)(*)()(21t f t f t f =,则)0(f 为( )A .1B .2C .3D .44.信号)()52(t u etj +-的傅里叶变换为( )A.ωω+5j e j 21 B. ω-ω+2j e j 51 C.)5(j 21+ω+ D. )5(j 21-ω+- 5.已知信号f t ()如图所示,则其傅里叶变换为( )A .τωττωτ2422Sa Sa ()()+ B .τωττωτSa Sa ()()422+C .τωττωτ242Sa Sa ()()+ D .τωττωτSa Sa ()()42+6.有一因果线性时不变系统,其频率响应H j j ()ωω=+12,对于某一输入x(t)所得输出信号的傅里叶变换为Y j j j ()()()ωωω=++123,则该输入x(t)为( )A .)(3t u e t --B .)(3t u e t -C .)(3t u e t -D .)(3t u e t7.)()(2t u e t f t =的拉氏变换及收敛域为( )A .122s s +>-,Re{}B .122s s +<-,Re{}C .122s s ->,Re{}D .122s s -<,Re{} 8.23)(2++=s s s s F 的拉氏反变换为( )A .)(]2[2t u e e t t --+B .)(]2[2t u e e t t ---C .)()(2t u e t t -+δD .)(2t u e t -9.离散信号)(n f 是指( )A . n 的取值是连续的,而)(n f 的取值是任意的信号B .n 的取值是连续的,而)(n f 的取值是离散的信号C .n 的取值是连续的,而)(n f 的取值是连续的信号D .n 的取值是离散的,而)(n f 的取值是任意的信号10. 已知序列f(n)=)1()21(---n u n ,其z 变换及收敛域为( )A. F(z)=122-z z z <21B. F(z)=z z 212- z >21C. F(z)=1-z z z <21 D. F(z)=1-z z z <1二. 填空题(本大题共10小题,每小题2分,共20分)1.)3()2(+*-t u t u =_ _ 。

2011《信号与系统》习题集选择题1.图示电路的微分方程是:(A )()()()t v t v t v c c =+'2(B )()()()t v t v t v c c =+'2(C )()()()t v t v t v c c =+'(D )()()()t v t v t v c c2=+'2.f[n]*δ(n-n 0)是 A f[n] B f (n-n 0) C δ(n-n 0) D δ(n ) 3下列傅里叶变换对中错误的是:A .1)(↔δFt B .222a a eFta +ω↔-C .)(1)(ωδ+ω↔Ft uD .aj t u eFat+ω↔-1)(4.下列拉普拉斯变换性质中错误的是A .时移特性)()(00s F e t t f st L-↔-B .S域微分特性dss dF t tf L)()(↔C .时域微分特性)()(s sF dtt df L↔ D .时域卷积特性)()()()(s H s F t h t f L↔*5.已知信号f (t )的波形如图所示,则f (t )的表达式为 (A)(t +1)ε(t) (B)δ(t -1)+(t -1)ε(t)(C)(t -1)ε(t) (D)δ(t +1)+(t +1)ε(t)6.若系统的起始状态为0,在x (t )的激励下,所得的响应为 (A )强迫响应;(B )稳态响应; (C )暂态响应;(D )零状态响应。
7.理想不失真传输系统的传输函数H (jω)是 (A )0j t Ke ω- (B )0tj Ke ω-(C )0t j Ke ω-[]()()c c u u ωωωω+-- (D )00j t Ke ω- (00,,,c t k ωω为常数)8.不满足)()(n u n 与δ之间满足如下关系(A )∑∞-∞=-=k k n n u )()(δ (B )∑∞=-=0)()(k k n n u δ(C ))1()()(--=n u n u n δ (D )()()(1)n u n u n δ=----9.中图所示的离散时间信号用单位阶跃信号u[n]表示的是 A f[n]=u[n+3]-u[n+1] B f[n]=u[n]-u[n+3] C f[n]=u[n]-u[n-1]D f[n]=u[n]-u[n-3](t v ππ--2)(t v R Ω1CF1)(t v cf (n )1 12 3n-1 010.下列信号是因果信号的是() 11.图示电路的微分方程是: (A )()()()t u t u t u s c c 2=+'(B )2()()()t u t u t u s c c =+'(C )()()()t u t u t u s c c=+'2 (D )()()()t u t u t u s c c=+'12.信号f (t )变成)121(+t f 的过程为 (A) 先将f (t )的图形向左移一个单位,再时间上展宽1/2倍。
信号与系统练习题集 第一部分:信号与系统的时域分析一、填空题 1. =---)3()()2(t t u et δ ( ).2. The unit step response )(t g is the zero-state response when the input signal is ( ).3. Given two continuous – time signals x(t) and h(t), if their convolution is denoted by y(t), then the convolution of )1(-t x and )1(+t h is ( ).4. The convolution =+-)(*)(21t t t t x δ( ).5. The unit impulse response )(t h is the zero-state response when the input signal is ( ).6. A continuous – time LTI system is stable if its unit impulse response satisfies the condition: ( ) .7. A continuous – time LTI system can be completely determined by its ( ). 8.=⎰∞∞-(t)dt 2sin 2δtt( ). 9. Given two sequences }1,2,2,1{][=n x and }5,6,3{][=n h , their convolution =][*][n h n x ( ).10. Given three LTI systems S1, S2 and S3, their unit impulse responses are )(1t h , )(2t h and )(3t h respectively. Now, construct an LTI system S using these three systems: S1 parallel interconnected by S2, then series interconnected by S3. the unit impulse response of the system S is ( ). 11. It is known that the zero-stat response of a system to the input signal x(t) is ⎰∞-=td x t y ττ)()(,then the unit impulse response h(t) is ( ).12. The complete response of an LTI system can be expressed as a sum of its zero-state response and its ( ) response.13. It is known that the unit step response of an LTI system is )(2t u et-, then the unit impulse response h(t) is( ).14. =++-=⎰∞dt t t t t x ))1()1((2sin )(0δδπ( ).15. We can build a continuous-time LTI system using the following three basic operations:( ) , ( ), and ( ).16. The zero-state response of an LTI system to the input signal )1()()(--=t u t u t x is)1()(--t s t s , where s(t) is the unit step response of the system, then the unit impulse response ish(t) = ( ).17. The block diagram of a continuous-time LTI system is illustrated in the following figure. The differentialequationdescribingtheinput-outputrelationshipofthesystemis( ).18. The relationship between the unit impulse response h(t) and unit step response s(t) is s(t) =( ), or h(t) = ( ).二、选择题1. For each of the following equations, ( ) is true.A 、)()()1(t t t δδ=-B 、)(2)1()1(t t t δδ=-+C 、⎰∞∞-=+)()()1(t dt t t δδ D 、⎰∞∞-=++1)1()1(dt t t δ2. Given two continuous-time signals )(t x and )(t h , if the convolution of )(t x and )(t h is denoted by )(t y , then the convolution of signals )1(+t x and )2(-t h is ( ).A. )(t yB. )1(-t yC. )2(-t yD. )1(+t y3. The unit impulse response of an LTI system is h(t) = te-, this system is ( ).)(tA. causal and stableB. causal and unstableC. noncausal and unstableD. noncausal and stable4. dt t t t x )2()12()(112-+=⎰-δ = ( ).A. 1B. 3C. 9D. 05. For an LTI system, if the input signal is )(1t x , the corresponding output response is )(1t y , if the input signal is )(2t x , the corresponding output response is )(2t y . And if the input signal is)()(21t bx t ax +, the corresponding output response is )()(21t by t ay + ( a and b are arbitrary realnumbers ). Then the system is a ( ) system.A. linearB. causalC. nonlinearD. time – invariant6. )(*)(21t t t t x --δ = ( ).A. )(21t t t x --B. )(21t t t x +-C. )(21t t t x -+D. )(21t t t ++δ7. =⎪⎭⎫⎝⎛-+=⎰∞∞-dt t t t t x 6)sin ()(πδ ( ). A.6πB.16-πC. 216-πD. 216+π8. Given two sequences ][1n x and ][2n x , their lengths are M and N respectively. The length of theconvolution of ][1n x and ][2n x is ( ).A .MB .NC .N M +D .1-+N M9. The unit impulse response of a continuous-time LTI system is dtt d t t h )()(2)(δδ+=, the differential equation describing the input-output relation of this system is ( ).A.)()()(2t x dt t dy t y =+B. )()(2)(t x dtt dy t y =+ C. dt t dx t x t y )()(2)(+= D. dtt dx t x dt t dy )(2)()(+=10. The input-output relation of a continuous-time LTI system is described by the differential equation:dt t dx t x t y dt t dy dtt y d )()(2)(3)(2)(22+=++. The unit impulse response of the system h(t) ( ).A . does not include )(t δ B. includes )(t δ C. includesdtt d )(δ D. is uncertain 11. Signals )(1t x and )(2t x are shown in the following figures. The expression of the convolution)(*)()(21t x t x t x = is ( ).A. )1()1(--+t u t uB. )2()2(--+t u t uC. )1()1(+--t u t uD. )2()2(+--t u t u 12. The following block diagram represents a continuous-time LTI system. The unit impulse response h(t) satisfies ( ).A.)()()(t x t y dtt dy =+ B. )()()(t y t x t h -= C.)()()(t t h dtt dh δ=+ D. )()()(t y t t h -=δ13. The input-output relationship of a causal continuous-time system is described by the differential equation:dtt dx t y dt t dy )(2)(3)(=+, then the unit step response =)(t s ( ). A. )(23t u e t - B. )(213t u e t - C. )(23t u e t D. )(213t u e t -11(1)(1))(2t x⊕)(t x )t+三、综合题(分析、计算题)1. The input-output relationship of a continuous-time LTI system is described by the equation:τττd x e t y tt )2()()(-=⎰∞---,a. Determine the unit impulse response h(t) of the system.b. Determine the system response y(t) to the input signal )2()1()(--+=t u t u t x .2. Given an LTI system depicted in Figure 2. Assume that the impulse response of the LTI system is h(t) = e -t u(t), the input signal x(t) = u(t) - u(t-2). Determine and sketch theoutput response y(t) of the system by evaluating the convolution y(t) = x(t)*h(t).3. Remember the following identities:)(*)()(t t x t x δ= )(*)()(00t t t x t t x -=-δ)()(*)(00t t t t t δδδ=-+dtt dh t x t h dt t dx dt t dy )(*)()(*)()(== 4. Consider an LTI system S and a signal )1(2)(3-=-t u e t x t . If)()(t y t x →and)()(3)(2t u e t y dtt dx t -+-→, determine the impulse response h(t) of S.5. Let )5()3()(---=t u t u t x and )()(3t u e t h t -=, as illustrated in the Figure6.(a). Compute y(t) = x(t)*h(t).Figure 2)(t x t5)(t h t131(b). Compute g(t) = dx(t)/dt * h(t).(c). How is g(t) related to y(t)?6. Let ∑∞-∞=--=k tk t t u e t y )3(*)()(δShow that t Ae t y -=)( for 0 ≤ t < 3, and determine the value A. 7. A causal LTI system is described by the differential equation:)()()(2)(3)(22t x dtt dx t y dt t dy dt t y d +=++ If the input signal is )()(2t u e t x t -=, determine the zero-state response y(t) of the system.8. In this problem, we illustrate one of the most important consequences of the properties of linearity and time invariance. Specifically, once we know the response of a linear system or a linear time-invariant system to a single input or responses to several inputs, we can directly compute the responses to many other input signals.(a). Consider an LTI system whose response to the signal x 1(t) in Figure 9(a) is the signal y 1(t) illustrated in Figure 9(b). Determine and sketch carefully the response of the system to the input x 2(t) depicted in Figure 9(c).(b). Determine and sketch the response of the system considered in part (a) to the input x 3(t) shown in Figure 9(d).tt第二部分:信号与系统的频域分析一、填空题1. The frequency response of an ideal filter is given by ⎪⎩⎪⎨⎧<≥=πωπωω100,0100,2)(j H , if the input signalis )120cos(5)80cos(10)(t t t x ππ+=, the corresponding outputresponsey(t)=( ).2. The Fourier transform of signal )cos()(0t t x ω= is ( ).3. The Fourier transform of signal )6sin()(0πω+=t t x is ( ).4. Assume that the Fourier transform of )(t x is denoted as )(ωj X , then the Fourier transform of)()(0t x e t y t j ω= is )(ωj Y = ( ).5. The Fourier transform of a continuous – time periodic signal ∑∞-∞==k tjk kea t x 0)(ω is )(ωj X =( ).6. It is known that the Fourier transform of )(t x is 11)(+=ωωj j X , then the Fourier transform of )(t tx is ( ).7. The Fourier transform of signal )(t x is denoted as )(ωj X , the Fourier transform of )()1(t x t - is ( ).8. A time shifting leads to a ( ).9. The frequency responses of two LTI systems are assumed to be 1()H j ω and 2()H j ω, the frequency response of the interconnection of 1()H j ω cascaded by 2()H j ω is ()H j ω =( ).10. A time-domain compression corresponds to a frequency-domain ( ). 11. For a signal x(t), if the condition⎰∞∞-∞<dt t x )( is satisfied, then the Fourier transform of x(t)exists, this condition is ( ) but not ( ).12. Figure 12 shows a continuous-time signal )(t x , its Fourier transform is denoted as )(ωj X , then=)0(X ( ). (Without evaluating )(ωj X ).13. For a continuous-time LTI system, if the zero-state response of the systemtotheinputsignal)()(t u e t x t-= is)()()(2t u e t u e t y t t ---=, then the frequency response of the systemis =)(ωj H ( ).14. The Fourier transform of signal ttt x 4sin )(= is =)(ωj X ( ).15. The inverse Fourier transform of )(ωδ is =)(t x ( ).16. The frequency spectrum includes two parts, one is ( ), the other is ( ). 17. Let )(ωj X denote the Fourier transform of signal )(t x , then the Fourier transform of signal)4cos(*)32()(t tx t y += is =)(ωj Y ( ). (Expressed using )(ωj X ).18. Let )(ωj X denote the Fourier transform of signal )(t x , then the Fourier transform of signal)cos()()(t t x t y π= is =)(ωj Y ( ). (Expressed using )(ωj X ).19. The period of the periodic square wave increases, the space of the spectral lines ( ). 20. Consider a continuous-time ideal lowpass filter S whose frequency response is⎪⎩⎪⎨⎧>≤=1001001)(ωωωj HWhen the input to this filter is a signal x(t) with fundamental period T = π/6 and Fourier series coefficients ak, it is found that)()()(t x t y t x S =−→−For k ( ) it is guaranteed that a k = 0.21. Consider a continuous-time LTI system whose frequency response isωωωω)4sin()()(==⎰+∞∞--dt e t h j H tjIf the input to this system is a periodic signal ⎩⎨⎧<≤-<≤=841401)(t t t x with period T = 8, thecorresponding system output is y(t) = ( ).二、选择题1. The frequency response of an ideal lowpass filter is⎪⎩⎪⎨⎧>≤=πωπωω120,0120,2)(j H .If the input signal is )200cos(5)100cos(10)(t t t x ππ+=, the output response is )(t y = ( ).A. )100cos(10t πB. )200cos(10t πC. )100cos(20t πD. )200cos(5t π2. The Fourier transform of the rectangular pulse )1()1()(--+=t u t u t x is ( ).A. )(4ωSaB. )(2ωSaC. )2(2ωSaD. )2(4ωSa3. Let )(ωj X denote the Fourier transform of a signal )(t x , the Fourier transform of jt e t x )( is ( ).A. )(ωωj X e j -B. )(ωωj X e jC. ))1((-ωj XD. ))1((+ωj X4. Let )(ωj X denote the Fourier transform of signal )(t x , the Fourier transform of )1(-t x is ( ).A. )(ωωj X e j -B. )(ωωj X e jC. ))1((-ωj XD.))1((+ωj X5. The Fourier transform of the rectangular pulse )1()()(--=t u t u t x is ( ).A. 2)2(ωωjesa - B. 2)2(ωωjesa C. ωωj e sa -)( D. ωωj e sa )(6. The condition for signal transmission with no distortion is that ( ).A. The magnitude response is a constant in the passband.B. The phase response is a line cross the origin in the passband.C. The magnitude response is a constant and the phase response is a line cross the origin in the passband.D. The phase response is a constant and the magnitude response is a line cross the origin. 7. The bandwidth of a signal )(t x is 20KHz, the bandwidth of signal )2(t x is ( ).A.20KHzB.40KHzC.10KHzD.30KHz8. Let )(ωj X denote the Fourier transform of signal )(t x , the Fourier transform of dtt dx t )( is ( ).A.ωωωωd j dX j X )()(- B. ωωωωd j dX j X )()(+- C. ωωωωd j dX j X )()(-- D. ωωωωd j dX j X )()(+ 9. Let )(ωj X denote the Fourier transform of signal )(t x , the Fourier transform of)()(b atx t y += is ( ).A. ωωjab ej X a )( B. ωωjab eja X a -)( C. ωωa b j e a j X a )(1 D. ωωa bj e aj X a -)(1 10. Let )(ωj X denote the Fourier transform of signal )1()1()(--+=t u t u t x , then =)0(X ( ).A. 2B. πC.π21D. 4 11. Let )(ωj X denote the Fourier transform of signal )(t x , the Fourier transform of )1(t x - is( ).A .ωωj e j X )(--B .ωωj ej X -)( C .ωωj ej X --)( D .ωωj e j X )(-12. Let )(ωj X denote the Fourier transform of signal )(t x , the Fourier transform of)()()(a t t x t y -=δ is ( ).A. ωωja e j X -)(B. ωja e a x -)(C. ωωja e j X )(D. ωja e a x )(13. The Fourier transform of signal )()()(τδτδ-++=t t t x is =)(ωj X ( ).A. ωτcos 21B. ωτcos 2C. ωτsin 21D. ωτsin 214. Let ),()(t e t x tδ-= and ττd x t y t⎰∞-=)()(. The Fourier transform of y(t) is =)(ωj Y ( ).A.ωj 1 B. ωj C.)(1ωπδω+j D. )(1ωπδω+-j 15. Consider the square wave )21()21()(ττ--+=t u t u t x , as τ decreases, the width of the mainlobe of )(ωj X ( ).A. increasesB. decreasesC. does not changeD. can not be determined16. It is known that the bandwidth of x(t) is ω∆, the bandwidth of )12(-t x is ( ).A. ω∆2B. 1-ω∆C. ω∆21D. )(1-21ω∆ 17. The inverse Fourier transform of 01)(t j e aj j X ωωω+=is =)(t x ( ). A. )()()(0t u e t x t t a +-= B. )()(0)(0t t u e t x t t a +=+- C. )()(0)(0t t u e t x t t a -=-- D. )()()(0t u e t x t t a --=18. The Fourier transform of signal )(t x τ is )2()(τωτωτSa j X =, then the Fourier transform of signal)1()(-=t x t y τ is =)(ωj Y ( ).A. ωωωj e Sa j Y )()(=B. ωωωj e Sa j Y -=)()(C. ωωωj e Sa j Y )(2)(=D. ωωωj e Sa j Y -=)(2)(19. Given an LTI system with its frequency response 21)(+=ωωj j H , it is known that the Fourier transform of the output response y(t) is)3)(2(1)(++=ωωωj j j Y , the input signal )(t x =( ).A. )()(2t u e t x t -=B. )()(3t u e t x t --=-C. )()(3t u e t x t -=D. )()(3t u e t x t =20. The frequency response of an ideal lowpass filter is ⎩⎨⎧≥<=-22)(ωωωωj e j H , its unit impulse response is h(t) = ( ).A.)1(2sin -t t π B. )1()1(2sin --t t π C. )1(sin -t t π D. )1()1sin(--t t π三、综合题(分析、计算)1. Consider a continuous-time LTI system whose frequency response isωωω)4sin()(=j HIf the input to this system is a periodic signal ⎩⎨⎧<≤-<≤=841401)(t t t x with period T = 8, determinethe corresponding system output y(t).2. The fundamental frequency of a continuous-time periodic signal is ω0 = π, Figure 2 shows the spectral coefficients of x(t).(a) Write out the expression of x(t).(b) If x(t) is applied to an ideal highpass filter with frequencyresponse ⎩⎨⎧≥=otherwisej H ,015,1)(πωω,determine the output signal y(t).3. Figure 3.a illustrates a communication system. Let X 1(j ω) and X 2(j ω) denote the Fourier transforms of x 1(t) and x 2(t), respectively. It is known that ω1 = 4π, ω2 = 8π, and the frequency response of the ideal bandpass filter is H 1(j ω), the overall output response is y(t).••••kka ∠Figure 2(1). Plot the magnitude of the Fourier transform W(j ω) of w(t).(2). Choose an appropriate frequency ω3, so that the output response is y(t) = x 1(t); (3). Plot the magnitude responses of H 1(j ω) and H 2(j ω).4. Figure 4 shows the Fourier transform )(ωj X of a periodic continuous-time signal )(t x . (1). Write out the expression of )(t x .(2). Let ⎩⎨⎧≤=Otherwisej H ,012,1)(πωω be thefrequency response of an ideal lowpass filter, and )(t x is applied to the filter, determine the output response y(t) of the filter.。