计量经济学 第十章 联立方程组模型
- 格式:doc
- 大小:322.50 KB
- 文档页数:16


计量经济学之联立方程模型引言联立方程模型(Simultaneous Equation Model,简称SEM)是计量经济学中的一个重要分析工具,用于研究多个经济变量之间的相互关系。
通过建立一组方程,可以理解变量之间的联动效应,并进行预测和政策分析。
本文将介绍联立方程模型的基本概念、建模步骤和常见的估计方法等内容。
基本概念联立方程模型的定义联立方程模型是指由多个方程组成的一种数学模型,用于描述多个经济变量之间的关系。
每个方程都包含一个因变量和若干个解释变量,以及一个误差项。
联立方程模型的核心思想是通过解方程组,得到各个变量的估计值,进而分析它们之间的关系。
基本假设在建立联立方程模型时,需要对变量之间的关系进行假设。
常见的基本假设有:1.线性关系假设:方程中的变量之间的关系是线性的。
2.独立性假设:各个方程中的误差项是独立的,即它们之间不存在相关性。
3.零条件均值假设:解释变量的条件均值为零,即解释变量的期望与误差项无关。
4.同方差假设:各个方程中的误差项方差相等。
建模步骤建立联立方程模型的步骤如下:步骤一:确定变量根据研究主题和数据可获得的变量,确定需要建立模型的变量集合。
步骤二:构建方程根据经济理论和实际问题,构建联立方程模型的方程形式。
每个方程包含一个因变量和若干个解释变量。
步骤三:参数估计通过收集数据,对联立方程模型进行参数估计。
常用的估计方法有最小二乘估计(Ordinary Least Squares,简称OLS)和广义矩估计(Generalized Method of Moments,简称GMM)等。
步骤四:模型诊断对估计得到的模型进行诊断,检验模型的拟合优度、参数显著性和误差项的假设等。
常见的诊断方法有虚拟变量检验、异方差性检验和序列相关性检验等。
步骤五:模型解释与政策分析根据估计得到的模型结果,解释各个变量之间的关系,并进行政策分析。
可以利用模型进行预测和模拟,评估不同政策对经济变量的影响。


联立方程模型一、概念:联立方程模型系统将变量分为内生变量和外生变量两大类。
由系统决定的,同时也对模型系统产生影响,它会受到随机项的影响。
一般都是经济变量。
每一个内生变量的值都要利用模型中的全部方程才能决定。
外生变量:是不由系统决定的变量,是系统外变量,取值由系统外决定。
一般是确定性变量,或者是具有临界概率分布的随机变量,其参数不是模型系统研究的元素。
外生变量影响系统,但本身不受系统的影响。
外生变量一般是经济变量、条件变量、政策变量、虚变量。
注:联立方程模型中有多少个内生变量就必定有多少个方程:根据经济理论和行为规律建立的描述经济变量之间直接结构关系的计量经济学方程系统称为结构式模型。
结构方程的正规形式:将一个内生变量表示为其他内生变量、先决变量和随机干扰项的函数形式完备的结构式模型:g个内生变量、k个先决变量、g个结构方程行为方程:描述变量之间经验关系的方程,含有未知的参数和随机扰动项。
例如:凯恩斯收入决定模型中的消费函数制度方程:由法律、制度、政策等制度性规定的经济变量之间的函数关系,如税收方程。
恒等式:定义方程式和平衡方程。
简化式模型:用所有先决变量作为每个内生变量的解释变量所形成的模型。
参数关系体系:描述简化式参数与结构式参数之间的关系。
二、识别方程之间的关系有严格的要求,一个方程模型想要能估计,必须可识别。
∴进行模型的估计之前需要判断模型是否可以识别(即是否能被估计)。
1、识别的基本定义:是否具有确定的统计形式。
注:识别的定义是针对结构方程而言的。
模型中每个需要估计其参数的随机方程都存在识别问题。
如果一个模型中的所有随机方程都是可以识别的,则认为该联立方程模型系统是可以识别的。
反之不识别。
恒等方程由于不存在参数估计问题,所以也不存在识别问题。
但是,在判断随机方程的识别性问题时,应该将恒等方程考虑在内。
恰好识别:某一个随机方程只有一组参数估计量过度识别:某一个随机方程具有多组参数估计量方程的线性组合是否得到的新方程具有与消费方程相同的统计形式,决定了方程也是否是可以识别的。

第十章 联立方程组模型第一节 联立方程组模型概述一、问题的提出1、单一方程模型存在的条件是单向因果关系。
2、对于变量之间存在的双向因果关系,则需要建立联立方程组模型。
3、经济现象的表现多以系统或体系的形式进行,仅用单一方程来反映存在局限性。
二、联立方程组的概念1、联立方程组模型的定义。
由一个以上的相互联系的单一方程组成的系统(模型),每一个单一方程中包含了一个过多个相互联系(相互依存)的内生变量。
联立方程组表现的是多个变量间互为因果的联立关系。
联立方程组与单一方程的区别是估计联立方程组模型的参数必须考虑联立方程组所能提供的信息(包括联立方程组里方程之间的关联信息),而单一方程模型的参数估计仅考虑被估计方程自身所能提供的信息。
2、联立方程组模型的例子。
(1)一个均衡条件下市场供给与需求的关系。
)3()2(0)1(012101110s i d i ii s i ii d i Q Q u P Q u P Q =>++=<++=βββααα 称(1)式为需求方程,(2)式为供给方程,(3)式为供需均衡式;d i Q 表示需求量,s i Q 表示供给量,i P 表示价格,i i u u 21,分别为(1)式和(2)式的随机误差项。
按照经济学基本原理,商品的供给与商品的需求共同作用于价格,反过来,价格也要分别决定商品的供给与需求。
这就是方程(1)与方程(2)的作用机制,如果考虑了均衡条件,这又是方程(3)的作用。
因此,通过这一联立方程组将上述商品的供需与价格的相互作用过程得到了反映。
(2)一个凯恩斯宏观经济模型。
011012(4)(5)(6)t t tt t tt t t t C Y u I Y u T C I G ββαα=++=++=++ 式中,C 表示消费,Y 表示国民总收入(又GDP ,实际上它们是有区别的),I 表示私人投资,G 表示政府支出,u1、u2分别为消费函数和投资函数中的随机误差项。



CWYKW tPtttGt1O300000\0y21010001100(00010容易验证该矩阵的秩为5,与整个模型w G T T Y tGt t t t1t1竹000000V1V2V2E1000000000000000),从而是可以识别的。
°202300Gt 0 0 1 0 0)联立方程计量经济学模型的识别与估计Klein于1950年建立的旨在分析美国两次世界大战间经济发展的小型宏观计量经济学模型如下:消费:c t=%+〜n t+僞耳i+〜(%+%)+%投资:人=兀+久存+侑耳1+峡1+纭工资:叫=卩0+人(Y t+T t叫丿+卩2(I1+T t1“Gt1)+泾+妆收入:Y t=C t+I t+G t T t利润:n t=y t w pt w Gt资本存量:£=—+仪i其中,Y,C,/,%,%,〃,K,G,T,t分别代表收入、消费、投资、私人工资、政府工资、利润、资本存量、政府支出、税收与时间。
1)模型的识别该模型中的内生变量共6个,分别为Y,C,I,W p,n,K,外生变量分别为为“G,G,T,t,先决变量共9个,分别为为岭1〃…,K1,W Gt,G t,Tt,t,咚1,—对于该模型的识别过程如下:对于消费方其中未包含的变量在其他方程中对应系数所组成的矩阵I Y K K w G T T Y tt t t t1Gt1t t t1t1100传0000000V10V20V1E E V31100011000010*******(1011000000)容易验证该矩阵的秩为5,与整个模型系统的内生变量减1后相等,从而是可以识别的。
另一方面,由于k心=103=7>2=31=21,因此,消费方程是过度识别的。
对于投资方程,其中未包含的变量在其他方程中对应系数所组成的矩阵为:另一方面,由于k心=103=7>1=21=9t1,因此,投资方程是过度识别的。
对于工资方程,其中未包含的变量在其他方程中对应系数所组成的矩阵为:cIn K tttt10线001B0111000010(0101容易验证该矩阵的秩为5,与整个模型系统的内生变量减1后相等,从而是可以识别的。
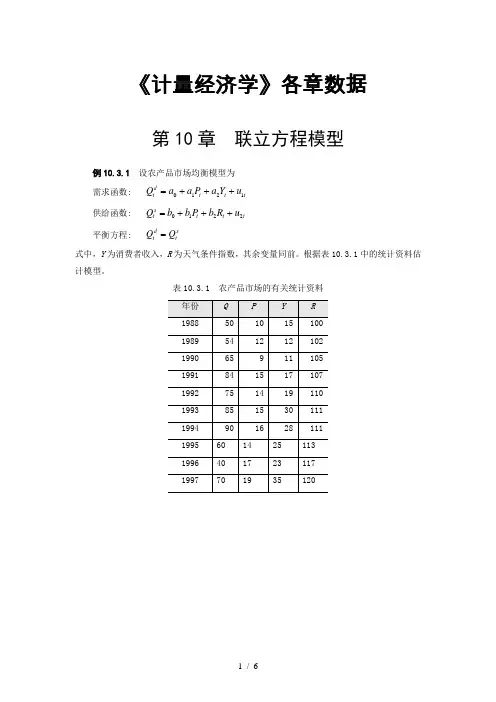
《计量经济学》各章数据第10章 联立方程模型例10.3.1 设农产品市场均衡模型为需求函数: t t t dt u Y a P a a Q 1210+++= 供给函数: t t t st u R b P b b Q 2210+++= 平衡方程: st d t Q Q =式中,Y 为消费者收入,R 为天气条件指数,其余变量同前。
根据表10.3.1中的统计资料估计模型。
表10.3.1 农产品市场的有关统计资料10.5 案例分析10.5.1 中国宏观经济模型中国1978-2003年居民宏观消费CONS、国内生产总值GDP、国内投资总额INV、政府支出GOV、净出口NEX(单位:亿元)统计数据,如表10.5.1所示:表10.5.1 中国宏观经济统计数据10.5.2 克莱因战争间模型根据美国1920~1941年的统计资料,如表10.5.6所示。
用2SLS和系统估计法等方法对模型参数进行估计。
表10.5.6 美国1920~1941年的统计数据思考与练习17.设我国的价格、消费、工资模型设定为t t t u I a a W 110++= t t t Pt u W b I b b C 2210+++= t pt t t t u C W I P 33210++++=γγγγ其中:I =固定资产投资(亿元);W =国营企业职工年平均工资(元);C =居民消费水平指数(%);P =价格指数(%)。
C 、P 均以上年为100%。
样本观察值如表2所示:表2 固定资产投资、职工平均工资与居民消费指数等统计资料(1)用递归模型参数估计法求出该模型的估计式;(2)用普通最小二乘法逐一估计每个方程;(3)比较以上两种做法的结果。
18.表3是我国1978-2003年国内生产总值(GDP )、货币供给量(2M )、政府支出(G )和投资支出(I )的统计资料,试用表中数据建立我国的收入——货币供给模型:t t t t t u G a I a M a a GDP 132210++++= t t t t u M b GDP b b M 2122102+++=-(1)判别模型的识别性。


第十章 联立方程组模型第一节 联立方程组模型概述一、问题的提出1、单一方程模型存在的条件是单向因果关系。
2、对于变量之间存在的双向因果关系,则需要建立联立方程组模型。
3、经济现象的表现多以系统或体系的形式进行,仅用单一方程来反映存在局限性。
二、联立方程组的概念1、联立方程组模型的定义。
由一个以上的相互联系的单一方程组成的系统(模型),每一个单一方程中包含了一个过多个相互联系(相互依存)的内生变量。
联立方程组表现的是多个变量间互为因果的联立关系。
联立方程组与单一方程的区别是估计联立方程组模型的参数必须考虑联立方程组所能提供的信息(包括联立方程组里方程之间的关联信息),而单一方程模型的参数估计仅考虑被估计方程自身所能提供的信息。
2、联立方程组模型的例子。
(1)一个均衡条件下市场供给与需求的关系。
)3()2(0)1(012101110s i d i ii s i ii d i Q Q u P Q u P Q =>++=<++=βββααα 称(1)式为需求方程,(2)式为供给方程,(3)式为供需均衡式;d i Q 表示需求量,s i Q 表示供给量,i P 表示价格,i i u u 21,分别为(1)式和(2)式的随机误差项。
按照经济学基本原理,商品的供给与商品的需求共同作用于价格,反过来,价格也要分别决定商品的供给与需求。
这就是方程(1)与方程(2)的作用机制,如果考虑了均衡条件,这又是方程(3)的作用。
因此,通过这一联立方程组将上述商品的供需与价格的相互作用过程得到了反映。
(2)一个凯恩斯宏观经济模型。
011012(4)(5)(6)t t tt t tt t t t C Y u I Y u T C I G ββαα=++=++=++ 式中,C 表示消费,Y 表示国民总收入(又GDP ,实际上它们是有区别的),I 表示私人投资,G 表示政府支出,u1、u2分别为消费函数和投资函数中的随机误差项。
三、联立方程组模型的基本问题(即联立方程组模型的偏倚性)1、内生解释变量与随机误差项的相关性。
2、直接对联立方程组模型运用OLS 法,所得的参数估计值是有偏的,并且是不一致的。
例如,设凯恩斯收入决定模型为[][]01)(11)1()0)(())(())())(((),cov(1)(11)1(11)(111)1(10122111110111011100110110≠-=-=-==-=--=-=-∴-+-=-+-+-=-+-+-=∴++=-+++=∴+=<<++=βσβββββββββββββββββββββU E U U E U E U Y E Y E U E U Y E Y E U Y U Y E Y I U E I Y E U I Y U I Y I U Y Y I C Y U Y C t t tt t tt t t t t t tt t tt t t tt t tt t表明内生变量Y 在作解释变量时与随机误差U 相关。
对凯恩斯模型中的消费函数求参数的估计,有(用离差形式表示)∑∑∑∑∑∑∑∑∑∑∑∑∑∑∑∑∑∑∑∑∑+==++=++===-=-=-=---=21221021022221)1()()0)(()()())((ˆy Uy yYy y Uy Yy y y y U Y y Cy Y Y y yy C Cy y y C C Y Y Y Y C C ββββββ求1ˆβ的数学期望 1211)()ˆ(βββ≠+=∑∑y Uy E E 在上式中,由于∑≠0)(Uy E ,所以,1ˆβ不是1β的无偏估计。
再看参数估计的一致性。
对1ˆβ的表达式两端同时求概率极限,得 1212121212111)lim()lim()lim()ˆlim(βσβσβββββ≠-+=+=+=+=∑∑∑∑∑∑Y ny n Uyp y Uy p y Uy p p表明1ˆβ不是1β的一致性估计。
下面根据此例用具体的数据(文件名kaiensimx )加以说明。
假定投资I 得数据已知,并且用蒙特卡罗方法生成随机误差U 得数据,再假定 0),cov(04.0)var(),0(0)(,0)(2===≠==-t t t s t t t I U U s U U E U E σ 进一步假定消费函数中得参数真实值已知为8.0,210==ββ。
(1)由8.0,210==ββ和U 的值,根据1110111ββββ-+-+-=t t t U I Y 计算Y 的数值;(2)由8.0,210==ββ、Y 的数值和U 的数值,根据消费函数计算C 的数值。
(3)由于用蒙特卡罗方法生成随机误差U 的数据,则样本误差应正好是“真实”误差,故求C 对Y 的回归,所得的参数估计就应是8.0ˆ,2ˆ10==ββ,与真实值一致。
(4)但当Y 与U 相关时,则参数估计的无偏性不再满足。
(Gujarati ,计量经济学,第641页)四、联立方程组模型中的几个概念1、内生变量。
其数值由模型体系所决定的变量称之为内生变量。
其特点是:(1)内生变量受模型体系的影响,反之亦然;(2)内生变量是随机变量。
2、前定变量。
包括外生变量和滞后内生变量。
外生变量是指,它取的数值不由模型体系所决定。
其特点是:(1)外生变量影响模型体系,反之不成立;(2)外生变量是非随机变量。
外生变量与内生变量的关系是:外生变量能够影响内生变量,但内生变量不能影响外生变量。
举例说明,(1)均衡条件下的供需模型;(2)凯恩斯的宏观经济模型。
1、 结构型模型。
根据经济学理论或现实经济活动,对某种经济结构或某种经济主体的行为运用数学关系式进行“直接”描述。
其过程可表述为 经济原型→数学模型为了简单起见,下面直接给出联立方程组模型结构型的矩阵形式(7)BY X U +Γ=其中,Y 为内生变量向量,X 为前定变量向量,U 为随机误差向量,B 为内生变量结构参数矩阵,Γ为前定变量结构参数矩阵(向量或矩阵的具体表示见教科书第211页)。
2、 简化型模型。
所谓简化型模型是指在联立方程组模型中每一个内生变量只由前定变量和随机误差线性表示,或者说内生变量只是前定变量和随机误差的函数。
用矩阵表示的过程如下,假设0B ≠,则1111(8)(9)Y B X B U B V B U Y X V----+Γ=∏=-Γ==∏+令有称(9)式为模型的简化型。
简化型模型与结构型模型的区别是:结构型模型中的方程左端为内生变量,但右端也可能出现内生变量;简化型模型中的方程左端为内生变量,但右端只有前定变量。
注意:在已知前定变量未来值的情况下,利用(9)式的样本估计式可直接对模型中的内生变量进行预测。
3、递归模型。
在结构型模型中,如果方程的结构按如下形式,即111112211221121122222331132231132233k k k k k k y x x x u y y x x x u y y y x x x u γγγβγγγββγγγ=++++=+++++=++++++则称为递归模型。
递归模型的特点是方便估计,无模型的识别问题。
第二节 联立方程组模型的识别问题一、识别的概念1、一个例子。
设凯恩斯宏观经济模型为)3()2()1(210110tt t tt t tt t I C Y u Y I u Y C +=++=++=ββαα 将(3)式变换为,)4(t t t C Y I -=将(4)式代入(2)式,得)5(210t t t t u Y C Y ++=-ββ将(5)式整理,得到如下模型:)6()1(210t t t u Y C --+-=ββ对比(1)式与(6)式,两个C 的表达式(均表示消费模型),对消费函数来讲表达式不惟一,究竟哪一个才是表达消费的函数,这就是所谓的识别问题。
再例如,同样是上述模型,将(1)式代入(3)式,得)7(11111)1(11110101101110t t t tt t tt t t tt t t u I Y u I Y u I Y Y I u Y Y αααααααααα-+-+-=++=-++=-+++= 比较(3)式与(7)式,国民总收入也有两个表达式,那么哪一个才是国民总收入的函数?不仅如此,(3)式为恒定式,而(7)式为一随机函数。
由凯恩斯宏观经济模型结构可知,该模型具有合理的经济学解释,即式(1)与(2)的参数,在所对应的经济意义解释上应该是惟一的,但经过一定的数学变换,我们发现事实并非如此。
比较式(2)与式(6),可以看出对于样本数据,,t t t C Y I ,均能得到参数0β与1β的估计0ˆβ与1ˆβ。
现在的问题是0ˆβ与1ˆβ究竟是投资函数(2)还是消费函数(6)的参数估计?这也是联立方程组模型的识别问题。
2、识别的定义。
总的原则是看方程组中一个方程与另一个方程有无差异,也就是看每一个方程出现的变量是否一致,如果出现在不同方程里的变量不一样,则方程为可识别,否则就不可识别。
关于识别的定义大致有以下几种情况:(1)方程的统计形式是否具有惟一型;(2)零系数规则;(3)结构型与简化型系数之间导出的关系。
本教科书仅从(3)给出识别的含义。
3、模型的识别问题。
只有当联立方程组中每一个(结构)方程是可识别的,则该方程组才是可识别的。
反之,当方程组模型中有一个方程不可识别,则整个方程组都不可识别。
相比较,以此判断方程组不可识别更容易。
4、联立方程组可估计的条件:内生变量的个数=联立方程组中方程的个数。
二、识别的类型下面通过几个例子来看利用结构型与简化型系数之间导出的关系所表现的识别类型。
1、不可识别。
设模型为)3()2(0)1(012101110s i d i ii s i ii d i Q Q u P Q u P Q =>++=<++=βββααα )4(11121100210110βαβααβββαα--+--=∴++=++∴=i i i ii i i si d i u u P u P u P Q Q 将(4)式代入(1)式或(2)得111121211121111011111000111121111011βαβαβαβαβαβαπβααβπβαβαβαβαβα--=--=--=--=--+--===i ii i i i i i s i d i i u u v u u v u u Q Q Q 令 则简化型模型为)6()5(2110i i ii v Q v P +=+=ππ由结构型与简化型系数之间的关系可以看出,简化型模型的系数只有两个,而结构型模型的系数有四个,显然要由简化型系数解出结构型系数是不可能的,即每一个结构方程都是不可识别,从而整个方程组不可识别。
如果在此基础上引入前定变量,则识别的状况会发生变化。