创新设计2011届高考数学理一轮复习随堂演练111复数的概念及运算

11-2 复数的概念与运算1.(2011·福建理，1)i 是虚数单位，若集合S ＝{－1,0,1}，则( ) A ．i ∈S B ．i 2∈S C ．i 3∈S D.2i∈S [答案] B[解析] i 2＝－1∈S ，故选B.2．(文)(2011·天津文，1)i 是虚数单位，复数1－3i1－i ＝( )A ．2－iB ．2＋iC ．－1－2iD ．－1＋2i[答案] A [解析]1－3i1－i＝1－3i 1＋i 1－i1＋i ＝4－2i2＝2－i.(理)(2011·安徽皖南八校联考)复数z 满足z ＝2－i 1－i ，则z －等于( )A ．1＋3iB ．3－i C.32－12i D.12＋32i [答案] C[解析] ∵z ＝2－i 1－i ＝2－i 1＋i 2＝3＋i2，∴z －＝32－12i ，故选C.3．(2011·揭阳一中月考)设a ，b 为实数，若复数1＋2ia ＋b i ＝1＋i ，则( )A ．a ＝32，b ＝12B ．a ＝3，b ＝1C ．a ＝12，b ＝32D ．a ＝1，b ＝3 [答案] A[解析] 1＋2i ＝(a ＋b i)(1＋i)＝a －b ＋(a ＋b )i ，∴⎩⎪⎨⎪⎧a －b ＝1a ＋b ＝2，∴⎩⎪⎨⎪⎧a ＝32b ＝12，故选A.4．(文)(2011·山东济南一模)设a 是实数，且a 1＋i ＋1－i2是实数，则a 等于( )A.12 B ．－1 C ．1 D ．2[答案] B [解析] ∵a1＋i ＋1－i 2＝a 1－i 2＋1－i2＝1＋a 2－1＋a2i 是实数， 又∵a ∈R ，∴1＋a 2＝0，∴a ＝－1.(理)(2011·山东潍坊一模)复数z ＝2＋m i1＋i (m ∈R)是纯虚数，则m ＝( )A ．－2B ．－1C ．1D ．2[答案] A [解析] 因为z ＝2＋m i1－i2＝2＋m 2＋m －22i 是纯虚数，所以⎩⎪⎨⎪⎧2＋m ＝0，m －2≠0.得m＝－2.5．(2010·广东江门调研)已知复数z ＝a ＋i(其中a ∈R ，i 为虚数单位)的模为|z |＝2，则a 等于( )A ．1B ．±1 C. 3 D ．± 3[答案] D[解析] ∵|z |＝2，∴a 2＋1＝4，∴a ＝± 3.6．(文)(2011·安徽文，1)设i 是虚数单位，复数1＋a i2－i 为纯虚数，则实数a 为( )A ．2B ．－2C ．－ 12D.12[答案] A [解析]1＋a i2－i＝1＋a i 2＋i 2－i2＋i＝2－a ＋2a ＋1i 5＝2－a 5＋2a ＋15i 为纯虚数，∴⎩⎪⎨⎪⎧2－a 5＝02a ＋15≠0，∴a ＝2.(理)(2011·温州八校期末)若i 为虚数单位，已知a ＋b i ＝2＋i 1－i (a ，b ∈R)，则点(a ，b )与圆x 2＋y 2＝2的关系为( )A ．在圆外B ．在圆上C ．在圆内D ．不能确定[答案] A[解析] ∵a ＋b i ＝2＋i 1－i ＝2＋i 1＋i2＝12＋32i(a ，b ∈R)， ∴⎩⎪⎨⎪⎧a ＝12b ＝32，∵⎝ ⎛⎭⎪⎫122＋⎝ ⎛⎭⎪⎫322＝52>2， ∴点P ⎝ ⎛⎭⎪⎫12，32在圆x 2＋y 2＝2外，故选A.7．规定运算⎪⎪⎪⎪⎪⎪ab cd ＝ad －bc ，若⎪⎪⎪⎪⎪⎪z i －i2＝1－2i ，设i 为虚数单位，则复数z ＝________. [答案] 1－i[解析] 由已知可得⎪⎪⎪⎪⎪⎪zi －i2＝2z ＋i 2＝2z －1＝1－2i ，∴z ＝1－i . 8．(2011·无为中学月考)已知复数z 1＝－1＋2i ，z 2＝1－i ，z 3＝3－2i ，它们所对应的点分别为A 、B 、C .若OC →＝xOA →＋yOB →，则x ＋y 的值是________．[答案] 5[解析] ∵OC →＝xOA →＋yOB →，∴(3－2i )＝x (－1＋2i )＋y (1－i )，∴⎩⎪⎨⎪⎧－x ＋y ＝32x －y ＝－2，解得⎩⎪⎨⎪⎧x ＝1y ＝4，故x ＋y ＝5.9．(2010·上海大同中学模考)设i 为虚数单位，复数z ＝(12＋5i)(cos θ＋isin θ)，若z ∈R ，则tan θ的值为________．[答案] －512[解析] z ＝(12cos θ－5sin θ)＋(12sin θ＋5cos θ)i ∈R ， ∴12sin θ＋5cos θ＝0，∴tan θ＝－512.10．(2010·江苏通州市调研)已知复数z ＝a 2－7a ＋6a ＋1＋(a 2－5a －6)i (a ∈R)．试求实数a分别为什么值时，z 分别为：(1)实数； (2)虚数； (3)纯虚数．[解析] (1)当z 为实数时，⎩⎪⎨⎪⎧a 2－5a －6＝0a ＋1≠0，∴a ＝6，∴当a ＝6时，z 为实数．(2)当z 为虚数时，⎩⎪⎨⎪⎧a 2－5a －6≠0a ＋1≠0，∴a ≠－1且a ≠6，故当a ∈R ，a ≠－1且a ≠6时，z 为虚数．(3)当z 为纯虚数时，⎩⎪⎨⎪⎧a 2－5a －6≠0a 2－7a ＋6＝0a ＋1≠0∴a ＝1，故a ＝1时，z 为纯虚数.11.(文)(2011·东北四市统考)已知复数z 1＝cos23°＋isin23°和复数z 2＝cos37°＋isin37°，则z 1·z 2为 ( )A.12＋32i B.32＋12i C.12－32i D.32－12i [答案] A [解析]z 1·z 2＝cos23°cos37°－sin23°sin37°＋(sin 37°cos23°＋cos37°sin23°)i＝cos60°＋i·sin60°＝12＋32i ，故选A.(理)若z ＝cos θ＋i sin θ(i 为虚数单位)，则使z 2＝－1的θ值可能是( )A.π6B.π4C.π3D.π2[答案] D[解析] ∵z 2＝cos2θ＋i sin2θ＝－1，∴⎩⎪⎨⎪⎧cos2θ＝－1sin2θ＝0.∴2θ＝2k π＋π (k ∈Z)， ∴θ＝k π＋π2.令k ＝0知，D 正确．12．如果复数(m 2＋i )(1＋mi )是实数，则实数m 等于( ) A ．1 B ．－1 C. 2 D ．－ 2[答案] B[解析] ∵(m 2＋i )(1＋mi )＝(m 2－m )＋(m 3＋1)i 是实数，m ∈R ， ∴由a ＋bi (a 、b ∈R)是实数的充要条件是b ＝0， 得m 3＋1＝0，即m ＝－1.13．(2011·南通调研)若复数z 满足z ＋i ＝3＋ii ，则|z |＝________.[答案]17[解析] ∵z ＝3＋ii －i ＝－3i ＋1－i ＝1－4i ，∴|z |＝17.14．在复平面内，z ＝cos10＋isin10的对应点在第________象限． [答案] 三[解析] ∵3π<10<7π2，∴cos10<0，sin10<0，∴z 的对应点在第三象限．15．(文)设复数z ＝lg(m 2－2m －2)＋(m 2＋3m ＋2)i ，当实数m 取何值时． (1)z 是纯虚数． (2) z 是实数．(3)z 对应的点位于复平面的第二象限．[解析] (1)由题意知⎩⎪⎨⎪⎧lg m 2－2m －2＝0，m 2＋3m ＋2≠0.解得m ＝3.所以当m ＝3时，z 是纯虚数．(2)由m 2＋3m ＋2＝0，得m ＝－1或m ＝－2， 又m ＝－1或m ＝－2时，m 2－2m －2>0， 所以当m ＝－1或m ＝－2时，z 是实数．(3)由⎩⎪⎨⎪⎧lg m 2－2m －2<0，m 2＋3m ＋2>0.解得：－1<m <1－3或1＋3<m <3.(理)设z 是虚数，ω＝z ＋1z是实数，且－1<ω<2.(1)求z 的实部的取值范围；(2)设u ＝1－z1＋z ，那么u 是不是纯虚数？并说明理由．[解析] (1)设z ＝a ＋bi (a 、b ∈R ，b ≠0)，ω＝a ＋bi ＋1a ＋bi ＝⎝ ⎛⎭⎪⎫a ＋a a 2＋b 2＋⎝ ⎛⎭⎪⎫b －b a 2＋b 2i ，∵ω是实数，∴b －ba 2＋b 2＝0.又b ≠0，∴a 2＋b 2＝1，ω＝2a . ∵－1<ω<2，∴－12<a <1，即z 的实部的取值范围是⎝ ⎛⎭⎪⎫－12，1. (2)u ＝1－z 1＋z ＝1－a －bi 1＋a ＋bi ＝1－a 2－b 2－2bi 1＋a 2＋b 2＝－b a ＋1i ， ∵－12<a <1，b ≠0，∴u 是纯虚数．16．将一颗质地均匀的正方体骰子(六个面的点数分别为1,2,3,4,5,6)先后抛掷两次，记第一次出现的点数为a ，第二次出现的点数为b .(1)设复数z ＝a ＋bi (i 为虚数单位)，求事件“z －3i 为实数”的概率；(2)求点P (a ，b )落在不等式组⎩⎪⎨⎪⎧a －b ＋2≥00≤a ≤4b ≥0表示的平面区域内(含边界)的概率．[解析] (1)z ＝a ＋bi (i 为虚数单位)，z －3i 为实数，则a ＋bi －3i ＝a ＋(b －3)i 为实数，则b ＝3.依题意得b 的可能取值为1,2,3,4,5,6，故b ＝3的概率为16.即事件“z －3i 为实数”的概率为16.(2)连续抛掷两次骰子所得结果如下表：1 2 3 4 5 6 1 (1,1) (1,2) (1,3) (1,4) (1,5) (1,6) 2 (2,1) (2,2) (2,3) (2,4) (2,5) (2,6) 3 (3,1) (3,2) (3,3) (3,4) (3,5) (3,6) 4 (4,1) (4,2) (4,3) (4,4) (4,5) (4,6) 5 (5,1) (5,2) (5,3) (5,4) (5,5) (5,6) 6(6,1)(6,2)(6,3)(6,4)(6,5)(6,6)由上表知，连续抛掷两次骰子共有36种不同的结果． 不等式组所表示的平面区域如图中阴影部分所示(含边界)．由图知，点P (a ，b )落在四边形ABCD 内的结果有：(1,1)、(1,2)、(1,3)、(2,1)、(2,2)、(2,3)、(2,4)、(3,1)、(3,2)、(3,3)、(3,4)、(3,5)、(4,1)、(4,2)、(4,3)、(4,4)、(4,5)、(4,6)，共18种．所以点P (a ，b )落在四边形ABCD 内(含边界)的概率为P ＝1836＝12.1．(2011·罗源一中月考)已知复数z 1＝cos α＋i sin α，z 2＝sin β＋i cos β，(α，β∈R)，复数z ＝z 1·z －2的对应点在第二象限，则角α＋β所在象限为( )A ．第一象限B ．第二象限C ．第三象限D ．第四象限[答案] C[解析] ∵z ＝(cos α＋i sin α)·(sin β－i cos β)＝sin(α＋β)－i cos(α＋β)的对应点在第二象限，∴⎩⎪⎨⎪⎧sin α＋β<0－cos α＋β>0，∴角α＋β的终边在第三象限．2．(2010·安徽合肥市质检)已知复数a ＝3＋2i ，b ＝4＋xi (其中i 为虚数单位，x ∈R)，若复数ab∈R ，则实数x 的值为( )A ．－6B ．6 C.83 D ．－83[答案] C [解析] a b ＝3＋2i 4＋xi ＝3＋2i 4－xi 16＋x 2＝12＋2x 16＋x 2＋⎝ ⎛⎭⎪⎫8－3x 16＋x 2·i ∈R ，∴8－3x 16＋x2＝0，∴x ＝83. 3．(2010·泰安市质检)若复数2＋ai1－i (a ∈R)是纯虚数(i 是虚数单位)，则a 的值为( )A ．－2B ．－1C ．1D ．2[答案] D [解析] 2＋ai1－i ＝2＋ai 1＋i 1－i 1＋i ＝a ＋2i ＋2－a2为纯虚数，∴⎩⎪⎨⎪⎧2－a ＝0a ＋2≠0，∴a ＝2.4．若i 是虚数单位，则满足(p ＋q i)2＝q ＋p i 的实数p 、q 一共有( ) A ．1对 B ．2对 C ．3对 D ．4对[答案] D[解析] 由(p ＋q i)2＝q ＋p i 得(p2－q 2)＋2pq i ＝q ＋p i ，所以⎩⎪⎨⎪⎧p 2－q 2＝q ，2pq ＝p .解得⎩⎪⎨⎪⎧p ＝0q ＝0，或⎩⎪⎨⎪⎧p ＝0q ＝－1，或⎩⎪⎨⎪⎧ p ＝32q ＝12，或⎩⎪⎨⎪⎧p ＝－32q ＝12，因此满足条件的实数p 、q 一共有4对．5．设A 、B 为锐角三角形的两个内角，则复数z ＝(cot B －tan A )＋i (tan B －cot A )对应点位于复平面的第________象限.[答案] 二[解析] 由于0<A <π2，0<B <π2且A ＋B >π2∴π2>A >π2－B >0 ∴tan A >cot B ，cot A <tan B 故复数z 对应点在第二象限．6．关于x 的不等式mx 2－nx ＋p >0(m ，n ，p ∈R)的解集为区间(－53，2)，则复数m ＋ni 所对应的点位于复平面内的第________象限．[答案] 三[解析] ∵mx 2－nx ＋p >0(m 、n 、p ∈R)的解集为(－53，2)，∴⎩⎪⎨⎪⎧m <0－53＋2＝n m>0－53×2＝p m<0，∵m <0，∴p >0，n <0.故复数m ＋ni 所对应的点位于复平面内的第三象限．7．(2011·上海文，19)已知复数z 1满足(z 1－2)(1＋i)＝1－i(i 为虚数单位)，复数z 2的虚部为2，且z 1·z 2是实数，求z 2.[解析] 设z 1＝(a ＋2)＋b i ，a ，b ∈R ，∵(z 1－2)(1＋i)＝1－i ，∴a －b ＋(b ＋a )i ＝1－i.∴⎩⎪⎨⎪⎧a －b ＝1a ＋b ＝－1∴⎩⎪⎨⎪⎧a ＝0b ＝－1，∴z 1＝2－i.又设z 2＝c ＋2i ，c ∈R ，则z 1z 2＝(2－i)(c ＋2i)＝(2c ＋2)＋(4－c )i ∵z 1z 2∈R ，∴4－c ＝0，c ＝4，∴z 2＝4＋2i.。

第七节 复数的的概念一、复习目标：1、了解数系的扩充过程，体会实际需求与数学内部的矛盾（数的运算规则、方程理论）在数系扩充过程中的作用；2、理解复数的基本概念以及复数相等的充要条件。

二、重难点：1.重点：理解并掌握复数的有关概念(复数集、代数形式、虚数、纯虚数、实部、虚部、复数相等)。

2.难点：复数的有关概念的应用。

三、教学方法：探析归纳，讲练结合四、教学过程（一）、谈新考纲要求及新课标高考命题考查情况，促使积极参与复数部分考查的重点是复数的有关概念、复数的代数形式、运算及运算的几何意义，一般是选择题、填空题，难度不大，预计今后的高考还会保持这个趋势。

预测2010年高考对本讲的试题难度不会太大，重视对基本问题诸如：复数的四则运算的考查，题目多以选择、填空为主。

（二）、知识梳理，方法定位（学生完成复资P148页填空题，教师准对问题讲评）1、复数的定义：形如(,)a bi a b R +∈的数叫复数，a 叫复数的实部，b 叫复数的虚部.全体复数所成的集合叫做复数集，用字母C 表示2、复数的代数形式: 复数通常用字母z 表示，即(,)z a bi a b R =+∈，把复数表示成a bi +的形式，叫做复数的代数形式.3、复数与实数、虚数、纯虚数及0的关系：对于复数(,)a bi a b R +∈，当且仅当0b =时，复数(,)a bi a b R +∈是实数a ；当0b ≠时，复数z a bi =+叫做虚数；当0a =且0b ≠时，z bi =叫做纯虚数；当且仅当0a b ==时，z 就是实数04、复数集与其它数集之间的关系：N Z Q R C 苘苘5、两个复数相等的定义：如果两个复数的实部和虚部分别相等，那么我们就说这两个复数相等.这就是说，如果a ，b ，c ，d R ∈，那么a bi c di +=+⇔a c =,b d =6、复数的模：设oz =bi a +,则向量oz 的长度叫做复数bi a +的模（或绝对值），记作bi a +. (1)22b a bi a z +=+=；(2)1212Z Z Z Z ∙=∙；(3)2121z z z z =；7．共扼复数：如果两个复数的实部相等，而虚部互为相反数，则这两个复数互为共扼复数。

第5讲复数的概念及运算随堂演练巩固1.若复数ii,则等于( )A.4+2iB.2+iC.2+2iD.3+i【答案】 A【解析】∵ii,∴i)(3-i)=3-i+3i-ii.故选2.已知i R),其中i为虚数单位,则a+b等于( )A.-1B.1C.2D.3【答案】 B【解析】∵i,∴a+2i=b i+i.∴a+2i=-1+b i.由复数相等知a=-1,b=2,∴a+b=1,选B.3.若R,i为虚数单位,且(a+i)i=b+i,则( )A.a=1,b=1B.a=-1,b=1C.a=1,b=-1D.a=-1,b=-1【答案】 C【解析】由(a+i)i=b+i,得a i-1=b+i,所以a=1,b=-4.复数等于( )A.iB.-iC.iD.i【答案】 A【解析】∵i,∴i.5.已知复数i对应的点在复平面坐标系的第二、四象限的角平分线上,则实数a= . 【答案】 -2【解析】 i=-1-(a+1)i.由题意知a+1=-1,∴a=-2.课后作业夯基基础巩固1.i是虚数单位,复数等于( )A.1+2iB.2+4iC.-1-2iD.2-i【答案】 A【解析】 i.2.如果i)(1+m i)是实数,则实数m等于( )A.1B.-1C.D.【答案】 B【解析】方法一:i)(1+m ii+i+m i m+i.∵i)(1+m i)为实数,∴.∴m=-1.方法二:代入验证法.将m=-1代入检验,可知.方法三:若i)(1+m i)为实数,则i)(1+m i)=i)(1-m i),求解可知.3.在复平面内,复数对应的点位于( )A.第一象限B.第二象限C.第三象限D.第四象限【答案】 D【解析】 i,对应的点为(1,-1),故选D.4.复数等于( )A.2-iB.1-2iC.-2+iD.-1+2i【答案】 C【解析】 i.5.已知复数是z的共轭复数,则等于( )A. B. C.1 D.2【答案】 A【解析】方法一:∵∴.∴.方法二:∵∴|z|.∴|z|.6.i是虚数单位,若i R),则ab的值是( )A.-15B.-3C.3D.15【答案】 B【解析】∵i,∴a=-1,b=3,ab=-3.7. i为虚数单位等于 ( )A.0B.2iC.-2iD.4i【答案】 A【解析】=0.8.已知0<a<2,复数z的实部为a,虚部为1,则|z|的取值范围是( )A.(1,5)B.(1,3)C.D.【答案】 C【解析】 |z|∵0<a<2,∴.9.设复数z满足z(2-3i)=6+4i(i为虚数单位),则z的模为 .【答案】 2【解析】z(2-3i)=6+4i,∴i.故|z|.10.复数z=x+y i R)满足|z-1|=x,则复数z对应的点Z(x,y)的轨迹方程为 . 【答案】【解析】由|z-1|=x,得|(x-1)+y i|=x,所以整理,得.11.(2011上海春招,14)为求解方程的虚根,可以把原方程变形为再变形为由此可得原方程的一个虚根为 .【答案】中的一个【解析】由题意可知,22432-++++=-+++++++1], (1)(1)(1)(1)[()(2)()x x ax x bx x x a b x ab x a b x比较二次项、三次项系数知解得或由此得原方程的一个虚根为中的一个.12.当实数m取何值时,复数i)-[4+(5m+6)i]为实数?为虚数?为纯虚数?【解】先把复数z整理成(1)当即m=-1或m=6时,z是实数(2)当即且时,z是虚数(3)当即∴m=4时,z是纯虚数.13.已知复数满足(1+i)=1-i(i为虚数单位),复数的虚部为2,且是实数,求【解】∵i)=1-i,∴i.设i R.i)(a+2i)=(2a+2)+(4-a)i.∵R,∴a=4,∴i.14.已知复数i(1)求;(2)若△ABC的三个内角A、B、C依次成等差数列,且cosA+2icos求||的取值范围. 【解】 i.(2)在△ABC中,由于内角A、B、C依次成等差数列,∴B=60,A+C=120.又cosA+2icosi=cosA+(2cosi=cosA+icosC,∴||coscos=cos(A+C)cos(A-C)+1=1+cos120cos(A-C)cos(A-C).由于A+C=120,∴A-C=120-2C.∴-120<A-C<120.∴cos.也就是||即||.拓展延伸15.设z是虚数是实数,且.(1)求|z|的值及z的实部的取值范围;(2)设求证:u为纯虚数;(3)求的最小值.【解】(1)∵z是虚数,∴可设z=x+y i R,且∴iii.∵是实数且∴.∴即|z|=1.此时.∵∴-1<2x<2,从而有.即z的实部的取值范围是.(2)证法一:2222221(i)(1i)(1x yi)12i 111i1(1)(1)x y x y x y y y zuz x y xx y x y-+--+-----=====-++++++++i,∵∴.∴u为纯虚数.证法二:∵z为虚数,且|z|=1,∴=1,即z. .∴u为纯虚数.2x+∵∴1+x>0.于是当且仅当2即x=0时等号成立.∴的最小值为1,此时i.。

2011届高考数学第一轮复习精品试题：复数选修1-2 第3章 数系的扩充与复数的引入 §3.1复数的概念重难点：理解复数的基本概念；理解复数相等的充要条件；了解复数的代数表示法及其几何意义．考纲要求：①理解复数的基本概念． ②理解复数相等的充要条件．③了解复数的代数表示法及其几何意义．经典例题： 若复数1z i =+，求实数,a b 使22(2)az bz a z +=+。

（其中z 为z 的共轭复数）．当堂练习： 1.0a =是复数(,)a bia b R +∈为纯虚数的（ ）A ．充分条件 B.必要条件 C.充要条件 D.非充分非必要条件 2设1234,23z i z i=-=-+，则12z z -在复平面内对应的点位于（ ）A.第一象限B.第二象限C.第三象限D.第四象限3．=+-2)3(31i i（ ）A ．i 4341+ B ．i 4341-- C ．i 2321+ D ．i 2321-- 4．复数z 满足()1243i Z i +=+，那么Z ＝（ ）A ．2＋iB ．2－iC ．1＋2iD ．1－2i5.如果复数212bii -+的实部与虚部互为相反数，那么实数b 等于（ ）A. 2B.23C.2D.－236.集合｛Z ︱Z ＝Z n i i n n ∈+-,｝，用列举法表示该集合，这个集合是（ ）A ｛0，2，－2｝ B.｛0，2｝C.｛0，2，－2，2i ｝D.｛0，2，－2，2i ，－2i ｝7.设O 是原点，向量,OA OB →→对应的复数分别为23,32i i --+，那么向量BA →对应的复数是（ ）.55A i -+ .55B i -- .55C i + .55D i -8、复数123,1z i z i=+=-，则12z z z =⋅在复平面内的点位于第（ ）象限。

A ．一 B.二 C.三 D .四 9.复数2(2)(11)()a a a ia R --+--∈不是纯虚数，则有（ ）.0A a ≠ .2B a ≠ .02C a a ≠≠且 .1D a =-10.设i 为虚数单位，则4(1)i +的值为 （ ）A ．4 B.－4 C.4i D.－4i11.设i z i C z 2)1(,=-∈且（i 为虚数单位），则z= ；|z|= .12.复数21i +的实部为 ，虚部为 。

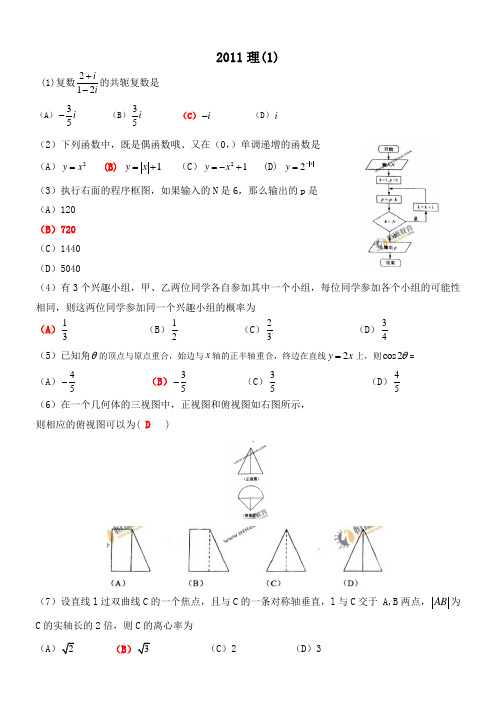
2011理(1)(1)复数212ii+-的共轭复数是 （A ）35i - （B ）35i （C ）i - （D ）i（2）下列函数中，既是偶函数哦、又在（0，）单调递增的函数是（A ）2y x = (B) 1y x =+ （C ）21y x =-+ (D) 2x y -= （3）执行右面的程序框图，如果输入的N 是6，那么输出的p 是 （A ）120 （B ）720 （C ）1440 （D ）5040（4）有3个兴趣小组，甲、乙两位同学各自参加其中一个小组，每位同学参加各个小组的可能性相同，则这两位同学参加同一个兴趣小组的概率为（A ）13 （B ）12 （C ）23 （D ）34（5）已知角θ的顶点与原点重合，始边与x 轴的正半轴重合，终边在直线2y x =上，则cos 2θ=（A ）45- （B ）35- （C ）35 （D ）45（6）在一个几何体的三视图中，正视图和俯视图如右图所示， 则相应的俯视图可以为( D )（7）设直线l 过双曲线C 的一个焦点，且与C 的一条对称轴垂直，l 与C 交于 A,B 两点，AB 为C 的实轴长的2倍，则C 的离心率为（A ）（B （C ）2 （D ）3（8）512a x x x x ⎛⎫⎛⎫+- ⎪⎪⎝⎭⎝⎭的展开式中各项系数的和为2，则该展开式中常数项为（A ）-40 （B ）-20 （C ）20 （D ）40（9）由曲线y =2y x =-及y 轴所围成的图形的面积为 （A ）103 （B ）4 （C ）163（D ）6 （10）已知a 与b 均为单位向量，其夹角为θ，有下列四个命题12:10,3P a b πθ⎡⎫+>⇔∈⎪⎢⎣⎭ 22:1,3P a b πθπ⎛⎤+>⇔∈⎥⎝⎦3:10,3P a b πθ⎡⎫->⇔∈⎪⎢⎣⎭ 4:1,3P a b πθπ⎛⎤->⇔∈ ⎥⎝⎦其中的真命题是（A ）14,P P （B ）13,P P （C ）23,P P （D ）24,P P （11）设函数()sin()cos()(0,)2f x x x πωϕωϕωϕ=+++><的最小正周期为π，且()()f x f x -=，则（A ）()f x 在0,2π⎛⎫ ⎪⎝⎭单调递减 （B ）()f x 在3,44ππ⎛⎫⎪⎝⎭单调递减 （C ）()f x 在0,2π⎛⎫⎪⎝⎭单调递增（D ）()f x 在3,44ππ⎛⎫⎪⎝⎭单调递增 (12)函数11y x =-的图像与函数2sin (24)y x x π=-≤≤的图像所有焦点的横坐标之和等于 （A ）2 (B) 4 (C) 6 (D)8（13）若变量,x y 满足约束条件329,69,x y x y ≤+≤⎧⎨≤-≤⎩则2z x y =+的最小值为 -6 。

章末总结知识点考纲展示复数❶理解复数的基本概念，理解复数相等的充要条件．❷了解复数的代数表示法及其几何意义．❸会进行复数代数形式的四则运算，了解复数代数形式的加、减运算的几何意义．算法与程序框图❶了解算法的含义，了解算法的思想．❷理解程序框图的三种基本逻辑结构：顺序、条件分支、循环；理解几种基本算法语句——输入语句、输出语句、赋值语句、条件语句、循环语句的含义．框图❶了解程序框图、工序流程图(即统筹图)与结构图．❷能绘制简单实际问题的流程图，了解流程图在解决实际问题中的作用．❸会运用结构图梳理已学过的知识，整理收集到的资料信息．合情推理与演绎推理❶了解合情推理的含义，能利用归纳和类比等进行简单的推理，了解合情推理在数学发现中的作用．❷了解演绎推理的重要性；掌握演绎推理的基本模式，并能运用它们进行一些简单推理．❸了解合情推理和演绎推理之间的联系和差异．直接证明与间接证明❶了解直接证明的两种基本方法——分析法和综合法；了解分析法和综合法的思考过程、特点．❷了解间接证明的一种基本方法——反证法；了解反证法的思考过程、特点．考点考题考源复数的几何意义(2016·高考全国卷Ⅰ，T2，5分)设(1＋2i)(a＋i)的实部与虚部相等，其中a为实数，则a＝()A．－3 B．－2C．2 D．3选修1-2P60练习T1(3)复数的运算与几何意义(2017·高考全国卷Ⅱ，T2，5分)(1＋i)(2＋i)＝()A．1－i B．1＋3iC．3＋i D．3＋3i选修1-2P60练习T1(2)复数的运算(2017·高考全国卷Ⅰ，T3，5分)下列各式的运算结果为纯虚数的是()A．i(1＋i)2B．i2(1－i)选修1-2P59例3(2)C ．(1＋i)2D ．i(1＋i)程序框图(2015·高考全国卷Ⅱ，T 8，5分)下边程序框图的算法思路源于我国古代数学名著《九章算术》中的“更相减损术”．执行该程序框图，若输入的a ，b 分别为14，18，则输出的a ＝( )A ．0B ．2C ．4D ．14必修3 P 36例1(2017·高考全国卷Ⅱ，T 8，5分)执行如图的程序框图，如果输入的a＝－1，则输出的S ＝( )A ．2B ．3C ．4D ．5必修3 P 41例4、P 42程序框图推理与证明(2017·高考全国卷Ⅲ，T 19，12分)如图，四面体ABCD 中，△ABC 是正三角形，AD ＝CD ．(1)证明：AC ⊥BD ；(2)已知△ACD 是直角三角形，AB ＝BD ．若E 为棱BD 上与D 不重合的点，且AE ⊥EC ，求四面体ABCE 与四面体ACDE 的体积比． 必修2 P 79B 组T 1一、选择题1．(选修1-2 P61A组T5(4)改编)i为虚数单位，则5i（2＋i）等于()A．－2－i B．－2＋i C．－1＋2i D．－1－2i解析：选D．5i（2＋i）＝5－1＋2i＝5（－1－2i）5＝－1－2i．2．(选修1-2 P33内文改编)有一个游戏：将标有数字1、2、3、4的四张卡片分别随机发给甲、乙、丙、丁4个人，每人一张，并请这4个人在看自己的卡片之前进行预测：甲说：乙或丙拿到标有3的卡片；乙说：甲或丙拿到标有2的卡片；丙说：标有1的卡片在甲手中；丁说：甲拿到标有3的卡片．结果显示甲、乙、丙、丁4个人的预测都不正确，那么甲、乙、丙、丁4个人拿到卡片上的数字依次为()A．3、4、2、1 B．4、2、1、3C．2、3、1、4 D．1、3、2、4解析：选B．由甲、丁的预测不正确可得丁拿到标有3的卡片，由乙的预测不正确可得乙拿到标有2的卡片，由丙的预测不正确可知甲拿到标有4的卡片，故丙拿到标有1的卡片，即甲、乙、丙、丁4个人拿到卡片上的数字依次为4、2、1、3．3．(选修1-2 P30练习T2改编)如图所示的数阵中，用A(m，n)表示第m行的第n个数，则依此规律A(15，2)为()131 61 61 10131101 15133013301151 2112131512121…A ．2942B ．710C ．1724D ．73102解析：选C ．由数阵知A (3，2)＝16＋16＝16＋23×4，A (4，2)＝16＋16＋110＝16＋23×4＋24×5，A (5，2)＝16＋16＋110＋115＝16＋23×4＋24×5＋25×6，…，则A (15，2)＝16＋23×4＋24×5＋25×6＋…＋215×16＝16＋2⎝⎛⎫13－14＋14－15＋…＋115－116＝16＋2⎝⎛⎫13－116 ＝16＋2×1348＝1724，选项C 正确． 4．(必修3 P 34－35案例1改编)如图所示的程序框图的算法思想源于数学名著《几何原本》中的“辗转相除法”，执行该程序框图(图中“m MOD n ”表示m 除以n 的余数)，若输入的m ，n 分别为495，135，则输出的m ＝( )A ．0B ．5C ．45D ．90解析：选C ．该程序框图是求495与135的最大公约数，由495＝135×3＋90，135＝90×1＋45，90＝45×2，所以495与135的最大公约数是45，所以输出的m ＝45，故选C ．二、填空题5．(选修1-2 P 61A 组T 3改编)ABCD 是复平面内的平行四边形，A 、B 、C 三点对应的复数分别为1＋2i ，－i ，2＋i ，O 为复平面原点，则|OD |＝________．解析：设D 点对应的复数为x ＋y i(x ，y ∈R )，因为ABCD 是平行四边形， 所以AB →＝DC →，即－i －(1＋2i)＝(2＋i)－(x ＋y i)， 即－1－3i ＝(2－x )＋(1－y )i ，所以⎩⎪⎨⎪⎧2－x ＝－11－y ＝－3，解得x ＝3，y ＝4．所以D 点对应的复数为3＋4i ． 所以|OD |＝|3＋4i|＝5， 答案：56．(选修1-2 P 44B 组T 1改编)已知sin α－cos αsin α＋2cos α＝－1，则tan 2α＝________．解析：由sin α－cos αsin α＋2cos α＝－1，可得2sin α＝－cos α，所以tan α＝－12，所以tan 2α＝2tan α1－tan 2α＝2×⎝⎛⎭⎫－121－⎝⎛⎭⎫－122＝－43． 答案：－43三、解答题7．(选修1-2 P 35B 组T 1改编)已知数列{a n }的前n 项和为S n ，a 1＝－23，且S n ＋1S n＋2＝a n (n ≥2)．计算S 1、S 2、S 3，并猜想S n ．解：n ＝1时，S 1＝a 1＝－23．n ＝2时，S 2＋1S 2＋2＝a 2＝S 2－S 1＝S 2＋23，所以S 2＝－34．n ＝3时，S 3＋1S 3＋2＝a 3＝S 3－S 2＝S 3＋34，所以S 3＝－45，所以猜想S n ＝－n ＋1n ＋2．8．(必修2 P 45探究、P 52B 组T 1(1)改编)一个正方体的平面展开图及该正方体的直观图的示意图如图所示：(1)请将字母F ，G ，H 标记在正方体相应的顶点处(不需说明理由)； (2)判断平面BEG 与平面ACH 的位置关系，并证明你的结论； (3)证明：直线DF ⊥平面BEG ． 解：(1)点F ，G ，H 的位置如图所示．(2)平面BEG ∥平面ACH ．证明如下：因为ABCD -EFGH 为正方体，所以BC ∥FG ，BC ＝FG ， 又FG ∥EH ，FG ＝EH ，所以BC ∥EH ，BC ＝EH ， 所以BCHE 为平行四边形． 所以BE ∥CH ．又CH ⊂平面ACH ，BE ⊄平面ACH ， 所以BE ∥平面ACH ． 同理BG ∥平面ACH ． 又BE ∩BG ＝B ，所以平面BEG ∥平面ACH ． (3)证明：连接FH ．因为ABCD-EFGH为正方体，所以DH⊥平面EFGH，因为EG⊂平面EFGH，所以DH⊥EG．又EG⊥FH，DH∩FH＝H，所以EG⊥平面BFHD．又DF⊂平面BFHD，所以DF⊥EG．同理DF⊥BG．又EG∩BG＝G，所以DF⊥平面BEG．。

第104-106课时：第十四章复数——复数的有关概念法及复数的运算法则，复数与实数的区别和联系。

三．教学过程：（一）主要知识：1.数的概念的发展，复数的有关概念（实数、虚数、纯虚数、复数相等、共轭复数、模）；2.复数的代数表示与向量表示；3.复数的加法与减法，复数的乘法与除法，复数的三角形式，复数三角形式的乘法与乘方，复数三角形式的除法与开方；4.复数集中解实系数方程（包括一元二次方程、二项方程）。

复数在过去几年里是代数的重要内容之一，涉及的知识面广，对能力要求较高，是高考热点之一。

但随着新教材对复数知识的淡化，高考试题比例下降，因此考生要把握好复习的尺度。

从近几年的高考试题上看：复数部分考查的重点是基础知识题型和运算能力题型。

基础知识部分重点是复数的有关概念、复数的代数形式、三角形式、两复数相等的充要条件及其应用，复平面内复数的几何表示及复向量的运算。

主要考点为复数的模与辐角主值，共轭复数的概念和应用。

若只涉及到一、二个知识点的试题大都集中在选择题和填空题；若涉及几个知识点的试题，往往是中、高档题目，解答此类问题一般要抓住相应的概念进行正确的变换，对有些题目，往往用数形结合可获得简捷的解法。

有关复数n次乘方、求辐角（主值）等问题，涉及到复数的三角形式，首先要将所给复数转化为三角形式后再进行变换。

复数的运算是高考中复数部分的热点问题。

主要考查复数的代数和三角形式的运算，复数模及辐角主值的求解及复向量运算等问题。

基于上述情况，我们在学习“复数”一章内容时，要注意以下几点：（1）复数的概念几乎都是解题的手段。

因此在学习复数时要在深入理解、熟练掌握复数概念上下功夫。

除去复数相等、模、辐角、共轭等外，还要注意一些重要而常不引起重视的概念。

如：若有“31zz+ 4”。

就是说1z Rz+∈，而且很快联系到111z z zz z+=+⇔=或z R∈，又∵1z=是不可能的，∴z R∈。

复数的三角形式和代数式，提供了将“复数问题实数化”的手段。