内蒙古海拉尔区第四中学2014届九年级数学9月月考试题

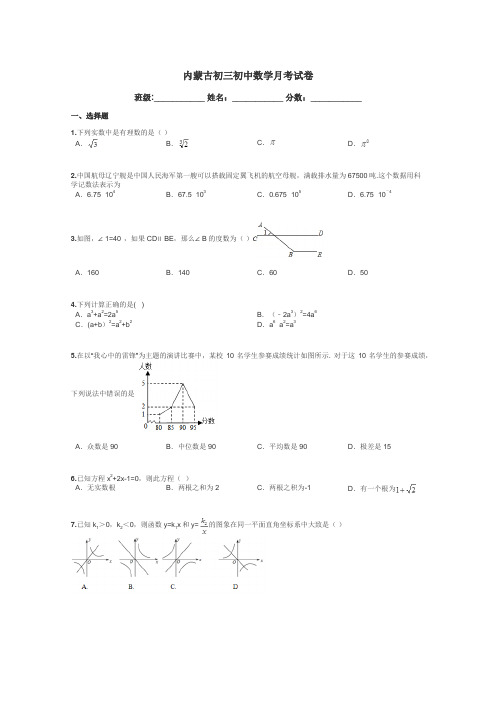
内蒙古初三初中数学月考试卷班级:___________ 姓名：___________ 分数：___________一、选择题1.下列实数中是有理数的是（ ）A ．B ．C ．D ．2.中国航母辽宁舰是中国人民海军第一艘可以搭载固定翼飞机的航空母舰，满载排水量为67500吨.这个数据用科学记数法表示为A ．6.75×104B ．67.5×103C ．0.675×105D ．6.75×10－43.如图，∠1=40°，如果CD ∥BE ，那么∠B 的度数为（ ）A ．160°B ．140°C ．60°D ．50°4.下列计算正确的是( )A ．a 3+a 2=2a 5B ．（﹣2a 3）2=4a6C ．(a+b ）2=a 2+b 2D ．a 6÷a 2=a 35.在以“我心中的雷锋”为主题的演讲比赛中，某校10名学生参赛成绩统计如图所示. 对于这10名学生的参赛成绩，下列说法中错误的是A ．众数是90B ．中位数是90C ．平均数是90D ．极差是156.已知方程x 2+2x-1=0，则此方程（ ）A ．无实数根B ．两根之和为2C ．两根之积为-1D ．有一个根为7.已知k 1＞0，k 2＜0，则函数y=k 1x 和y=的图象在同一平面直角坐标系中大致是（ ）8.如图，线段AB是⊙O的直径，弦CD丄AB，∠CAB=20°，则∠AOD等于（）A．160°B．150°C．140°D．120°9.已知二次函数的y=ax2+bx+c（a≠0）图象如图所示，有下列5个结论：①abc＜0；②b＜a+c；③4a+2b+c＜0；④2c＜3b；⑤a+b＞m（am+b）（m≠1的实数），其中正确结论的个数有（）A．2B．3C．4D．5二、填空题1.要使式子有意义，则x的取值范围是 .2.分解因式：a3﹣a= .3.若是方程的两个实数根，则_______。

蒙古海拉尔区第四中学2014届九年级11月月考数学试题（无答案） 一、选择题（本大题共10小题，每小题3分，共30分） 1、( )若二次根式12x +有意义,则x 的取值范围为:A.21≥x B. 21≤x C. 21-≥x D. 21-≤x2、 ( )下列图形中，是中心对称图形的是:3、（ ）平面直角坐标系内一点p(-2,3)关于原点对称点的坐标是A 、（3，-2）B 、（2，3）C 、（-2，-3）D 、（2，-3）4、（ ）下列一元二次方程中没有实数根的是：A ．0422=-+x xB ．0442=+-x xC ．0522=--x xD ．0432=++x x5、（ ）估算324+的值：A ．在5和6之间B ．在6和7之间C ．在7和8之间D ．在8和9之间6、（ ）已知：关于x 的一元二次方程有两个相等的实数根，其中R 、r 分别是⊙O 、 ⊙O 的半径，d 为两圆的圆心距，则⊙O 与⊙O 的位置关系是：A 、外离B 、外切C 、相交D 、内含。

7、( )如图，⊙O 中，ABDC 是圆内接四边形，∠BOC=110°，则∠BDC 的度数是：A.110°B.70°C.55°D.125°8、（ ）如图，将半径为8的⊙O 沿AB 折叠，弧AB 恰好经过与AB 垂直的半径OC 的中点D ，则折痕AB 长为：A.152B.154C.8D.109、（ ）P 为⊙O 外一点，PA 、PB 分别切⊙O 于A 、B ，CD 切⊙O 于点E ，分别交PA 、PB 于点C 、D ，若PA=5，则△PCD 的周长为A ．5B ．7C ．8D ．10 10、（ ）如图，如果从半径为9cm 的圆形纸片剪去13圆周的一个扇形，将留下的扇形围成一个圆锥（接缝处不重叠），那么这个圆锥的高为：A ．6cmB ．35cmC ．8cmD ．53cm二、填空题（本大题共8小题，每小题3分，共24分）11．当m= 时，方程是关于x 一元二次方程。

古海拉尔区第四中学2014届九年级3月月考数学试题一选择题：（每题3分，共36分）2．下列根式中属最简二次根式的是（ ）A 21a +B 12C 8D 23．下列计算错误．．的是 ( ) A ．1472= B ．60302= C ．9258a a a =D ．3223=4．用一个2倍的放大镜照一个ΔABC ，下列命题中正确的是（ ）A.ΔABC 放大后角是原来的2倍B.ΔABC 放大后周长是原来的2倍C.ΔABC 放大后面积是原来的2倍D.以上的命题都不对5．如图，小芳和爸爸正在散步，爸爸身高1.8m ，他在地面上的影长为2.1m ．若小芳比爸爸矮0.3m ，则她的影长为（ ）．A ．1.3mB ．1.65mC ．1.75mD ．1.8m2.1m太阳光线6．如图，四个边长为1的小正方形拼成一个大正方形，A 、B 、O 是小正方形顶点，⊙O 的半径为1，P 是⊙O 上的点，且位于右上方的小正方形内，则sin ∠APB 等于（ ）A ．32B ．22C ．12D ．17.下列说法中，正确的是（ ）①所有的等腰梯形都是相似图形；②所有的平行四边形都是相似图形；③所有P O第6题的圆都是相似图形；④所有的正方形都是相似图形；⑤所有的等腰三角形都是相似图形.A.①②④B.②③⑤C.③④⑤D.③④8.如图，小正方形的边长均为1，则图中三角形（阴影部分）与△ABC 相似的是( )9. 把二次函数23x y =的图象向左平移2个单位，再向上平移1个单位，所得到的图象对应的二次函数关系式是（ ）（A ）()1232+-=x y ; （B ）()1232-+=x y ; （C ）()1232--=x y （D ）()1232++=x y 10.如果关于x 的一元二次方程22(21)10k x k x -++=有两个不相等的实数根，那么k 的取值范围是（ ） A.14k >- B.14k >-且0k ≠ C.14k <- D.14k ≥-且0k ≠11.已知⊙O 1与⊙O 2的半径分别为3cm 和7cm ，两圆的圆心距O 1O 2 =10cm ，则两圆的位置关系是（ ）A ．外切B ．内切C ．相交D ．相离二填空题：（每题3分，共18分）13．如果1x -有意义，那么x 的取值范围是14．如果2180a -=，那么a 的算术平方根是15. 在平面直角坐标系中，△ABC 顶点A 的坐标为（2，3），若以原点O 为位似中心，画△ABC 的位似图形A B C '''△，使△ABC 与A B C '''△的相似比等于12 ，则点A ′的坐标为 ．16.一个口袋中有25个球，其中红球、黑球、黄球若干个，从口袋中随机摸出一AB球记下其颜色，再把它放回口袋中摇匀，重复上述过程，共试验200次，其中有120次摸到黄球，由此估计口袋中的黄球约有_ __个．17. 4sin tan 5ααα=若为锐角,且，则为 ( )18．如图所示，有一圆弧形桥拱，拱的跨度m 330=AB ，拱形的半径R ＝30m ，则拱形的弧长为______．(2)（5分）计算：1031)2(45sin 28-⎪⎭⎫ ⎝⎛--+-πο20. （7分）如图，△ABC 在方格纸中（1）请在方格纸上建立平面直角坐标系，使A （2，3），C （6，2），并求出B 点坐标；（2）以原点O 为位似中心，相似比为2，在第一象限内将△ABC 放大，画出放大后的图形△A ′B ′C ′；AB C（第22题）（3）计算△A′B′C′的面积S．21．（7分）如图所示，某人站在楼顶观测对面的笔直的旗杆AB．已知观测点C到旗杆的距离(CE的长度)为8m，测得旗杆的仰角∠ECA为30°，旗杆底部的俯角∠ECB为45°，求旗杆AB的高度是22. （7分）已知二次函数y＝－x2+4x.（1）用配方法把该函数化为y＝a(x－h)2 + k(其中a、h、k都是常数且a≠0)的形式，并指出函数图象的对称轴和顶点坐标；（2）函数图象与x轴的交点坐标.23．（7分）如图，把菱形ABCD沿着BD的方向平移到菱形A’B’C’D′的位置，(1)求证：重叠部分的四边形B’EDF’是菱形(2)若重叠部分的四边形B’EDF’的面积是菱形ABCD面积的一半,且BD=2，求则此菱形移动的距离．24．（8分）在一个不透明的盒子里，装有三个分别写有数字的小球，它们的形状、大小、质地等完全相同，先从盒子里随机取出一个小球，记下数字后放回盒子，摇匀后再随机取出一个小球，记下数字．请你用画树状图或列表的方法，求下列事件的概率：（1）两次取出小球上的数字相同；（2）两次取出小球上的数字之和大于10．26. （12分）如图1所示，在ABC △中，2AB AC ==，90A =o ∠，O 为BC 的中点，动点E 在BA 边上自由移动，动点F 在AC 边上自由移动．（1）点E F ，的移动过程中，OEF △是否能成为45EOF =o ∠的等腰三角形？若能，请指出OEF △为等腰三角形时动点E F ，的位置．若不能，请说明理由．（2）当45EOF =o ∠时，设BE x =，CF y =，求y 与x 之间的函数解析式，写出x 的取值范围．（3）在满足（2）中的条件时，若以O 为圆心的圆与AB 相切（如图2），试探究直线EF 与⊙O 的位置关系，并证明你的结论．。

姓名 考号试卷类型A2014年呼伦贝尔市初中毕业生学业考试数 学温馨提示：1．本试卷共6页，满分120分．考试时间120分钟．2．答卷前务必将自己的姓名、考号、座位号、试卷类型（A 或B ）涂写在答题卡上；选择题答案选出后，请用2B 铅笔把答题卡上对应题目的答案标号（ABCD ）涂黑，如需改动，请先用橡皮擦拭干净，再改涂其他答案；非选择题，请用0.5毫米的黑色字迹签字笔直接答在答题卡上．在试卷上作答无效．3．请将姓名与考号填写在本试卷相应位置上． 4．考试结束，将试卷、答题卡和草纸一并交回．一、选择题（下列各题的四个选项中只有一个正确．共12小题，每小题3分，共36分） 1．13-的倒数是A ．3B ．3-C ．13-D ．132．用3个相同的立方块搭成的几何体如图所示，它的主视图是A B C D正面3．下列各式计算正确的是A ．532x x x -=B ．336()mn mn =C ．222)(b a b a +=+D ．624p p p ÷=(0)p ≠4．在正方形、等腰三角形、矩形、菱形中，既是中心对称图形又是轴对称图形的有 A ．1个B ．2个C ．3个D ．4个5．下列事件是随机事件的是A ．通常情况温度降到0℃以下，纯净的水结冰；B ．随意翻到一本书的某页，这页的页码是偶数；C ．度量三角形的内角和，结果是360°；D ．测量某天的最低气温，结果为－180℃.6．如图，已知AB ∥CD ，∠2＝120°，则∠1的度数是A ．30°B ．60°C ．120°D ．150°7．一个多边形的每个内角均为108°，则这个多边形是A ．七边形B ．六边形C ．五边形D ．四边形8．九年级某班十名同学进行定点投篮测试，每人投篮六次，投中的次数统计如下：5，4，3，5，5，2，5，3，4，1，这组数据的中位数、众数分别为 A ．4，5B ．5，4C ．4，4D ．5，59．将点A （-2，-3）向右平移3个单位长度得到点B ，则点B 所处6 题图21 DCBA15题图O DCBA的象限是A ．第一象限B ．第二象限C ．第三象限D ．第四象限 10．一元二次方程220x x --=的解是A ．1221x x ==，B ．1221x x =-=，C ．1221x x ==-，D ．1221x x =-=-，11．如图，在水平地面上，由点A 测得旗杆BC 顶点C 的仰角为60°，点A 到旗杆的距离AB =12米，则旗杆的高度为A ．63米B ．6米C ．123米D ．12米12．如图，三个小正方形的边长都为1，则图中阴影部分面积的和是A ．34πB ．38πC ．32πD ．316π二、填空题（本题5个小题，每小题3分，共15分）13．在函数324y x =-中，自变量x 的取值范围是 .14．分解因式：293025a a -+= .15．如图，矩形ABCD 中，对角线AC 、BD 相交于点O ,6AC =，则OD = .16．用一个圆心角为120︒，半径为4的扇形作一个圆锥的侧面，则这60°11题图CBA12题图个圆锥底面圆的周长为 . 17．一组等式：22221223++=，22222367++=，2222341213++=，2222452021++=……请观察它们的构成规律，用你发现的规律写出第9个等式 .三、解答题（本题4个小题，每小题6分，共24分） 18．计算：201()122tan60(3)2π--+︒+-19．先化简，再求值：211(1)22x x x -+÷--，其中3x = 20．把形状、大小、质地完全相同的4张卡片分别标上数字-1、-4、0、2，将这4张卡片放入不透明的盒子中搅匀．求下列事件的概率：（1）从中随机抽取一张卡片，卡片上的数字是负数；（2）先从盒子中随机抽取一张卡片不放回，再随机抽取一张，两张卡片上的数字之积为0（用列表法或树形图）.21．如图，在平面直角坐标系中，已知一次函数y kx b =+的图象经过点A （1，0），与反比例函数m y x=（x ＞0）的图象相交于点B （2，1）.（1）求m 的值和一次函数y kx b =+的解析式；yx121题图OBA 12（2）结合所给图象直接写出：当x ＞0时，不等式kx b ＞m x的解集.四、（本题7分）22．某中学九（2）班同学为了了解2013年某小区家庭月均用水情况，随机调查了该小区的部分家庭，并将调查数据进行如下整理.请解答以下问题：（1）把上面的频数分布表和频数分布直方图补充完整； （2）求被调查的家庭中，用水量不超过15吨的家庭占总数的百分比；（3）若该小区有1000户家庭，根据调查数据估计，该小区月均用水量超过20吨的家庭大约有多少户?月均用水量x (吨) 频数 频率0﹤x ≤5 6 0.12 5﹤x ≤10 0.24 10﹤x ≤15 16 0.32 15﹤x ≤20 10 0.20 20﹤x ≤25 4 25﹤x ≤30 2 0.04 月均用水量（吨）频数5 10 15 20 25 3016 12 8 4 0五、（本题7分）23．从甲地到乙地的路有一段上坡，一段下坡．如果上坡平均每分钟走50米，下坡平均每分钟走100米，那么从甲地走到乙地需要25分钟，从乙地走到甲地需要20分钟．甲地到乙地上坡与下坡的路程各是多少？六、（本题8分）24．如图，在ABC ∆中，以AB 为直径的⊙O 交AC 于点M ，弦MN ∥BC 交AB 于点E ，且1,2,3ME AM AE ===．（1）求证：BC 是⊙O 的切线；（2）求⊙O 的半径．七、（本题10分）25．某商品的进价为每件20元，售价为每件25元时，每天可卖出250件．市场调查反映：如果调整价格，一件商品每涨价1元，每天要少卖出10件．（1）求出每天所得的销售利润w （元）与每件涨价x （元）之间的NABCM E O24题图DCFE F图2图1DCAO(E)ABO B函数关系式；（2）求销售单价为多少元时，该商品每天的销售利润最大； （3）商场的营销部在调控价格方面，提出了A ,B 两种营销方案.方案A ：每件商品涨价不超过5元； 方案B ：每件商品的利润至少为16元． 请比较哪种方案的最大利润更高，并说明理由．八、（本题13分）26．以AB 为直径作半圆O ，AB =10，点C 是该半圆上一动点，连接AC 、BC ，延长BC 至点D ，使DC =BC ，过点D 作DE⊥AB 于点E ，交AC于点F ，在点C 运动过程中：（1）如图1，当点E 与点O 重合时，连接OC ，试判断COB ∆的形状，并证明你的结论；（2）如图2，当DE =8时，求线段EF 的长；（3）当点E 在线段OA 上时，是否存在以点E 、O 、F 为顶点的三角形与ABC ∆相似？若存在，请求出此时线段OE 的长；若不存在，请说明理由.2014年呼伦贝尔市初中毕业生学业考试数学答案及评分标准试卷类型A一、选择题（每小题3分，共36分）试卷类型B一、选择题（每小题3分，共36分）题号 1 2 3 4 5 6 7 8 9 10 11 12 答案 A D C B A C B D A D D C二、填空题（每小题3分，共15分）13．2≠x 14．2(35)a - 15．3 16．38π 17．22229190109=++三、解答题（每小题6分，共24分）18．解：原式132324++-= …………（4分）题号 1 2 3 4 5 6 7 8 9 10 11 12 答案B C D C B B C A D C C B5=…………（6分）19．解：原式2)1)(1()212(--+÷-+-=x x x x x …………（2分）)1)(1(221-+-⨯--=x x x x x …………（3分）11+=x…………（4分）当3=x 时 原式41131=+=…………（6分）20．解：（1）设抽到卡片上的数字是负数记为事件A ，则21()42P A == …………（2分）（2）依题意列表（树形图）如下：…………（4分）故所有等可能结果有12种，其中两张卡片上的数字之积是0的结果有6种，设两张卡片上的数字之积是0为事件B ，则61()122P B == …………（6分）21．解：（1） 反比例函数)0(>=x xmy 的图象经过点B （2,1） 12m∴=∴2=m…………（1分）又 一次函数b kx y +=的图象经过A (1，0), B （2，1）∴⎩⎨⎧+=+=bk bk 210…………（3分）-1 -4 0 21- 4 0 -2 4-4 0 -80 00 2-2-8-8-2-84-20004积第二张-1-122-1200000-4-4-42-4-1第一张第一张第二张解得：⎩⎨⎧-==11b k ∴一次函数的解析式为：1y x =-…………（4分）（2）2>x…………（6分）四、（本题满分7分）22．解：（1）…………（3分） （2）%68%10024101612616126=⨯+++++++答：被调查的家庭中，用水量不超过15吨的家庭占总数的百分比是68%月均用水量xxx 频频0﹤x ≤5 6 0.15﹤x ≤10 12 0.210﹤x ≤15 16 0.315﹤x ≤20 10 0.220﹤x ≤25 4 0.025﹤x ≤30 2 0.0…………（5分） （3）120100024101612624=⨯++++++（户）答：该小区月均用水量超过20吨的家庭大约有120户. …………（7分） 五、（本题满分7分）23．解：设甲地到乙地上坡路x 米，下坡路y 米. …………（1分）根据题意，得25501002050100xy y x ⎧+=⎪⎪⎨⎪+=⎪⎩ …………（5分） 解得1000500x y =⎧⎨=⎩…………（6分） 答：甲地到乙地上坡路1000米，下坡路500米. …………（7分）六、（本题满分8分）24．（1）证明：∵在AME ∆中=AM 2 ，ME =1，3=AE∴222AE ME AM +=, ∴AME ∆是直角三角形∴︒=∠90AEM …………24题图O E M CBAN（2分）又 MN ∥BC∴︒=∠90ABC …………（3分）∴BC AB ⊥ 又 AB 是直径∴BC 是⊙O 的切线…………（4分）（2）解：连接OM ,设⊙O 的半径是r …………（5分）在OEMRt ∆中3OE r =- …………（6分）∴222(3)1r r =-+ …………（7分）∴233r =…………（8分）七、（本题满分10分）25．解：（1）根据题意得：(2520)(25010)w x x =+-- …………（2分）即：)250(1250200102≤≤++-=x x x w 或210(10)2250(025)w x x =--+≤≤ …………（3分）（2） 010<-，抛物线开口向下，二次函数有最大值 当10)10(22002=-⨯-=-=a b x 时，销售利润最大 此时销售单价为：10+25=35（元）答: 销售单价为35元时，该商品每天的销售利润最大.…………（5分）（3）由（2）可知，抛物线对称轴是直线10=x ，开口向下，对称轴左侧w 随x的增大而增大，对称轴右侧w 随x 的增大而减小方案A :根据题意得， 5≤x ∴50≤≤x 当5=x 时，利润最大最大利润为2000125052005102=+⨯+⨯-=w （元）………（7分）方案B ：根据题意得，162025≥-+x∴11≥x ∴2511≤≤x∴当x =11时，利润最大最大利润为224012501120011102=+⨯+⨯-=w （元）……（9分）20002240>∴综上所述，方案B 最大利润更高…………（10分） 八、（本题满分13分）26．(1)答：COB ∆是等边三角形 …………（１分）证明： AB DE ⊥∴︒=∠90DOB又 DC BC =∴BC OC = …………（2分）∴OB BC OC ==∴COB ∆是等边三角形…………（3分）(2)解：连接AD…………（4分）AB 为圆O 的直径∴︒=∠90ACB又 DC BC = ∴10==AB AD∴68102222=-=-=DE AD AE∴4EB = …………（5分）又 ︒=∠+∠︒=∠+∠90,90BDE B BAC B ∴BDE BAC ∠=∠F图1DC O(E)ABBO A图2EFCD∴AEF ∆∽DEB ∆ …………（6分）∴DEAE EB EF = …………（7分）∴864=EF ∴3=EF …………（8分）(3)答;存在当OEF ∆和ABC ∆相似时 ①如图3,若FOE CAB ∠=∠ 则AF OF = 又 AB DE ⊥ ∴252===OA AE OE …………（10分）②如图4，若CBA EOF ∠=∠ 则OF ∥BD∴21=BC OF ………（11分）∴41=BD OF ∴41==BD OF BE OE …………（12分）∴415=+OE OE ∴35=OE综上所述：OE 的长为25或35…………（13分）。

内蒙古海拉尔区第四中学2014届九年级物理9月月考试题（无答案）新人教版符合“绿色理念”的是（）A.就地焚烧B.发酵后作为农家肥C.加工成饮料瓶D.发酵制沼气2、如图所示为内燃机工作时的某冲程示意图，该冲程是（）A．吸气冲程 B．压缩冲程 C．做功冲程 D．排气冲程3、甲乙两台柴油机，甲的效率低于乙的效率，意义是（A.甲的功率大于乙的功率B.甲消耗的燃料多于乙消耗的燃料C.乙将燃料燃烧放出的能变成有用功的那部分能的比例比甲大D.工作相同时间甲消耗的燃料一定比乙少4、关于热机错误的说法是A.利用内能来做功的机器叫热机B.蒸汽机、内燃机、燃气轮机、喷气发动机都叫热机C.一切热机的工作过程都包括四个冲程D.用来做有用功的那部分能量和燃料完全燃烧放出的能量之比叫做热机的效率5、关于物体的内能，下列说法正确的是（）A．温度相等的1 kg和100 g的水内能相同 B．物体内能增加，一定要从外界吸收热量C．温度为0℃的物体没有内能 D．在相同物态下，同一物体温度降低，它的内能会减少6、下列现象中，属于热传递的方法改变物体内能的是（）A．刚从蒸笼里拿出的馒头，放一阵子变凉了B．冬天天冷，通过搓手发热取暖C．用锤子敲打石头时，锤子发热D．给自行车车胎打气，打气筒壁变热了7、在如图所示事例中，不属于．．．做功改变内能的是（）8、下列有关热现象的说法中，正确的是（）A．分子间既有引力又有斥力，分子间的距离越大作用力也越大B．机械能与整个物体的运动情况有关，内能与物体内部分子的热运动有关C．震后疾病防控消毒时空气中散发一股浓浓的药味，是药物分子的扩散现象D．做功和热传递都可以改变物体的内能，但功和热量是不同的物理量，单位也不同9、下列说法正确的是（）A．验电器既能检验物体是否带电，也能测出物体的带电量B．铜线中的电流是电子定向移动形成的C．绝缘体不容易导电是因为绝缘体内没有电子D．电源是把化学能转化为电能的装置10、用丝绸摩擦过的玻璃棒去靠近甲、乙两个轻小物体，结果甲被排斥、乙被吸引。

内蒙古海拉尔区第四中学2014届九年级9月月考数学试题（无答案） 新人教版一选择题、（每题3分，共36分）1、下列计算正确的是（ ） A 、2·3＝ 6 B 、2＋3＝ 6 C 、8＝3 2 D 、 4÷2＝22、已知一个正方形的面积是5，那么它的边长是 （ ）A 、5B 、5C 、51 D 、以上都不对 3.下列图形中，既是轴对称图形又是中心对称图形的是（ ）4.下列是中心对称图形的有（ ）（1）线段；（2）角；（3）等边三角形；（4）正方形；（5）平行四边形；（6）矩形；（7）等腰梯形． Ａ．2个 Ｂ．3个 Ｃ．4个 Ｄ．5个5.如图,将正方形图案绕中心O 旋转180°后,得到的图案是 ( )6.下列命题中的真命题是 ( )(A)全等的两个图形是中心对称图形. (B)关于中心对称的两个图形全等.(C)中心对称图形都是轴对称图形. (D)轴对称图形都是中心对称图形.7．方程0632=--x x 配方的结果为（ ） A 、()43332=-x B 、433232=⎪⎭⎫ ⎝⎛-x C 、()1532=-x D 、415232=⎪⎭⎫ ⎝⎛-x 8.如图，△ABC 绕点A 逆时针旋转后得到△AB ′C ′，若∠BAC ′=130°，∠BAC=80°，则旋转角等于（ ）A.30°B.50°C.80°D.210°9.一元二次方程2210x x --=的根的情况为（ ）A.有两个相等的实数根B.有两个不相等的实数根C.只有一个实数根D.没有实数根10.如果关于x 的一元二次方程22(21)10k x k x -++=有两个不相等的实数根，那么k 的取值范围是A.14k >-B.14k >-且0k ≠C.14k <-D.14k ≥-且0k ≠ （ ） 11．已知一个三角形的两边长是方程x 2-8x +15=0的两根，则第三边y 的取值范围是（ ）．A ．y<8B ．3<y<5 c ．2<y<8 D ．无法确定12.已知xy ＜0，则y x 2化简为 （ ） A.y x B.y x - C.y x - D.y x --二填空题（每小题3分，共24分）13.平面直角坐标系内一点P （－2，3）关于原点的对称点的坐标是 .14.当x 时，52+x 有意义.15、比较大小：56________75--。

内蒙古自治区呼和浩特市第四中学2024--2025学年九年级上学期数学月考试卷一、单选题1．下列各图中，四边形ABCD 是正方形，其中阴影部分两个三角形成中心对称的是（）A ．B ．C ．D ．2．对于二次函数()21y x =--的图象的特征，下列描述正确的是（）A ．开口向上B ．经过原点C ．对称轴是y 轴D ．顶点在x 轴上3．用配方法解一元二次方程2620x x -+=时，下列变形正确的是（）A ．()237x -=B ．()2311x -=C ．()237x +=D ．()231x -=4．已知二次函数224y x x =-++，关于该函数在22x -≤≤的取值范围内，下列说法正确的是（）A ．有最大值5，有最小值4-B ．有最大值0，有最小值4-C ．有最大值4，有最小值4-D ．有最大值4，有最小值05．抛物线277y kx x =--的图象和x 轴有两个交点，则k 的取值范围是（）A ．74k ≥-B ．74k >-C ．74k ≥-且0k ≠D ．74k >-且0k ≠6．某体育球类专卖店将进货单价为100元的某品牌篮球按零售价135元一个售出时，每天能卖出100个．若这种篮球的零售价在一定范围内每降价1元，其日销量就增加4个，要使顾客尽量得到实惠，且每天获得的利润为3596元，每个篮球需降价（）A ．4元B ．6元C ．4元或6元D ．5元7．要将抛物线2y x =平移后得到抛物线223y x x =++，下列平移方法正确的是（）A ．向左平移1个单位，再向上平移2个单位B ．向左平移1个单位，再向下平移2个单位C ．向右平移1个单位，再向上平移2个单位D ．向右平移1个单位，再向下平移2个单位8．在平面直角坐标系中，二次函数22y x mx m m =++-（m 为常数）的图像经过点(06)，，其对称轴在y 轴左侧，则该二次函数有（）A ．最大值5B ．最大值154C ．最小值5D ．最小值1549．若1x ，2x 是一元二次方程230x x +-=的两个实数根，则3221417-+x x 的值为（）A ．2-B ．6C ．4-D ．410．设二次函数()()y a x m x m k =---（0a >，m ，k 是实数），则（）A ．当2k =时，函数y 的最小值为a -B ．当2k =时，函数y 的最小值为2a -C ．当4k =时，函数y 的最小值为a -D ．当4k =时，函数y 的最小值为2a-二、填空题11．已知点A （﹣2，b ）与点B （a ，3）关于原点对称，则a ﹣b =．12．已知某抛物线上部分点的横坐标x ，纵坐标y 的对应值如下表：xL 2-1-012L yL503-4-3-L那么该抛物线的顶点坐标是．13．为增强学生身体素质，提高学生足球运动竞技水平，我市开展“市长杯”足球比赛，赛制为单循环形式（每两队之间赛一场）．现计划安排21场比赛，应邀请多少个球队参赛？设邀请x 个球队参赛，根据题意，可列方程为．14．如图，在平面直角坐标系中，抛物线23y ax bx =++与x 与相交于点A ，B ，点B 的坐标为(3,0)，若点(2,3)C 在抛物线上，则AB 的长为．15．如图1，一名男生推铅球，铅球的运动路线近似是抛物线的一部分，铅球出手位置的高度为5m 3，当铅球行进的水平距离为4m 时，高度达到最大值3m ．铅球的行进高度y （单位：m ）与水平距离x （单位：m ）之间的关系满足二次函数．若以最高点为原点，过原点的水平直线为x 轴，建立如图2所示的平面直角坐标系xOy ，该二次函数的解析式为2112y x =-．若以过出手点且与地面垂直的直线为y 轴，y 轴与地面的交点为原点，建立如图3所示的平面直角坐标系xOy ，则该二次函数的解析式为．16．已知某函数的图象过()2,1A -，()4,1B 两点，下面有四个推断：①若此函数的图象为直线，则此函数的图象经过()0,3-；②若此函数的图象为抛物线，且经过()3,0.5-，则该抛物线开口向下；③若此函数的解析式为()2(0)y a x h k a =-+≠，且经过()6,0，则45h <<；④若此函数的解析式为()2(0)y a x h k a =-+≠，开口向下，且24h <<，则a 的范围是12a <-．所有合理推断的序号是．三、解答题17．解方程：(1)2412981x x ++=；(2)2710x x --=；(3)()25410x x x -=-18．小王去年开了一家微店，今年1月份开始盈利，2月份盈利2400元，4月份盈利达到3456元，且从2月份到4月份，每月盈利的平均增长率相同，试求每月盈利的平均增长率．19．如图，在平面直角坐标系中，ABC V 的顶点()2,2A -，()0,5B ，()0,2C ．(1)将ABC V 以点C 为旋转中心旋转180︒得到11A B C ，请画出11A B C ；(2)平移ABC V ，若点A 的对应点2A 的坐标为()2,6--，请画出平移后的222A B C △；(3)若将11A B C 绕某一点旋转可以得到222A B C △，写出旋转中心的坐标：______；20．二次函数()20y ax bx c a =++≠的图像如图所示，根据图像填空：(1)方程20ax bx c ++=的两个根为_____________；(2)不等式20ax bx c ++>的解集为____________；(3)函数y 随x 的增大而减小的自变量x 的取值范围为____________；(4)若方程20ax bx c k +++=有两个不相等的实数根，k 的取值范围为____________．21．已知关于x 的一元二次方程x 2﹣（2k +1）x +k 2+2k ＝0有两个实数根x 1，x 2．（1）求实数k 的取值范围．（2）是否存在实数k ，使得x 1x 2﹣x 12﹣x 22＝﹣16成立？若存在，请求出k 的值；若不存在，请说明理由．22．如图，四边形ABCD 是一块边长为6米的正方形花圃，现将它改造为矩形AEFG 的形状，其中点E 在AB 边上（不与点B 重合），点G 在AD 的延长线上，3DG BE =，设BE 的长为x 米，改造后花圃AEFG 的面积为y 平方米．（1）当改造后花圃AEFG 的面积与原正方形ABCD 花圃的面积相等时，求BE 的长；（2）当x 为何值时，改造后的花圃AEFG 的面积最大?并求出最大面积．23．综合与实践问题情境：如图①，矩形MNKL 是学校花园的示意图，其中一个花坛的轮廓可近似看成由抛物线的一部分与线段AB 组成的封闭图形，点A ，B 在矩形的边MN 上．现要对该花坛内种植区域进行划分，以种植不同花卉，学校面向全体同学征集设计方案．方案设计：如图②，6AB =米，AB 的垂直平分线与抛物线交于点P ，与AB 交于点O ，点P 是抛物线的顶点，且9PO =米．欣欣设计的方案如下：第一步：在线段OP 上确定点C ，使90ACB ∠=︒，用篱笆沿线段AC BC ，分隔出ABC V 区域，种植串串红；第二步：在线段CP 上取点F （不与C ，P 重合），过点F 作AB 的平行线，交抛物线于点D ，E ．用篱笆沿DE CF ，将线段AC BC ，与抛物线围成的区域分隔成三部分，分别种植不同花色的月季．方案实施：学校采用了欣欣的方案，在完成第一步ABC V 区域的分隔后，发现仅剩6米篱笆材料．若要在第二步分隔中恰好用完6米材料，需确定DE 与CF 的长．为此，欣欣在图②中以AB 所在直线为x 轴，OP 所在直线为y 轴建立平面直角坐标系．请按照她的方法解决问题：(1)在图②中画出坐标系，并求抛物线的函数表达式；(2)求6米材料恰好用完时DE 与CF 的长；(3)种植区域分隔完成后，欣欣又想用灯带对该花坛进行装饰，计划将灯带围成一个矩形．她尝试借助图②设计矩形四个顶点的位置，其中两个顶点在抛物线上，另外两个顶点分别在线段AC BC ，上．直接写出符合设计要求的矩形周长的最大值．。

内蒙古海拉尔区第四中学2014届九年级上学期开学检测数学试题（无答案） 新人教版一、试一试，你一定能填上。

（36分）1、某计算机在1秒钟能进行七十亿五千零六万四千次计算，横线上的数写作（ ），四舍五入到亿位的近似数约是（ ）。

2、2.6小时 = （ ）时（ ）分 ，0.55立方米 = （ ）升。

3、如果在数轴上表示－2.5、1.125、－21、2这四个数，其中（ ）离0点最远。

4、某地区，50名非典型肺炎感染者中，其中有12名是医护人员，占总感染者的（ ）%。

感染的医护人员与其他感染者人数的比是（ ）：（ ）5、一段体积是42.9立方分米的圆柱形木料，切削成一个最大的圆锥体，削去部分的体积是（ ）立方分米6、一幅中国地图的比例尺是1：4500000，改写成线段比例尺是（ ），在这幅地图上，量得南京到北京的距离是20.4厘米，南京到北京的实际距离是（ ）千米。

7、把5米长的钢筋，锯成同样长的小段，共锯7次，每段占全长的（ ），每段长（ ）米。

如果锯成两段，需2分钟，锯成5段共需（ ）分钟。

8、体积和底面积都相等的圆柱和圆锥，圆柱的高与圆锥的高的比是（ ）。

9、一个圆锥体的体积是12立方分米，底面积是3平方分米，高是（ ）。

二、请你当公正的裁判官。

（10分）1、买同样重的苹果和梨，买苹果用了7元，买梨用了5元，那么苹果和梨的单价比是7:5。

( )2、一件儿童上衣原价100元，降价20%后，又涨价20%，此时这件儿童上衣售价不变。

( )3、自然数都有它的倒数。

（ ）4、两个面积相等的三角形，一定能拼成一个平行四边形。

( )5、小明说：“我表妹是1998年2月29日出生的。

（ ）三 、对号入座。

（10分）1、在下面平面图形中，对称轴最多的是（ ）。

A 、长方形B 、正方形C 、等边三角形D 、扇形2、下面几种说法，不正确的是（ ）A 、正方形面积与边长成反比例B 、圆是轴对称图形C 、正方形是特殊的长方形D 、画一条4厘米长的线段3、一个圆柱体，如果它的底面半径扩大2倍，高不变，那么它的体积扩大（ ）倍。

满分：120分一、选择题（共10道小题，每小题3分，共30分） 下面各题均有四个选项，其中只有一个．．是符合题意的． 1．下列图形中，是中心对称图形的是 （ ）A B C D 2．下列说法正确的是 ( )A. 掷两枚硬币，一枚正面朝上，一枚反面朝上是不可能事件 B ．随意地翻到一本书的某页，这页的页码为奇数是随机事件 C ．经过某市一装有交通信号灯的路口，遇到红灯是必然事件D ．某一抽奖活动中奖的概率为1001,买100张奖券一定会中奖3．下列运算正确的是（ ）A ．532=+B ．224=-C ．353332=+D ．925925-=-4．如图，AB 是⊙O 的直径，C ，D 两点在⊙O 上，若∠C ＝40°， 则∠ABD 的度数为A ．40°B ．50°C ．80°D ．90°5．上海世博会的某纪念品原价150元，连续两次涨价a %后售价为216元．下列所列方程中正确的是A ．150(1＋2a %)＝216B ．150(1＋a %)2＝216C ．150(1＋a %)×2＝216D ．150(1＋a %)＋150(1＋a %)2＝2166. 如图，已知△ABC 中，AB = AC ，∠ABC =70°，点I 是△ABC 的内心， 则∠BIC 的度数为A. 40°B. 70°C. 110°D. 140°7．一副三角板按图1所示的位置摆放，将△DEF 绕点A(F)逆时针旋转60°后（图2），测得CG ＝10cm ，则两个三角形重叠（阴影）部分的面积为A ．75cm 2B ．253cm 2C ．（25＋2533)cm 2 D ．（25＋5033)cm 28、若二次函数62+-=mx x y 配方后为k x y +-=2)2(，则k m ,的值分别为（ ）A 、0，6B 、0，2C 、4，6D 、4，29、一个小球被抛出后，距离地面的高度h （米）和飞行时间t （秒）满足下面函数关系式：()2516h t =--+，则小球距离地面的最大高度是（ ）.A 、1米B 、5米C 、 6米D 、 -5米10、已知二次函数y ＝ax 2＋bx ＋c （a ≠0）的图象如图，则下列结论中正确的是 A ．a c>0 B ．当x >1时，y 随x 的增大而增大 C ．2a ＋b ＝1 D ．方程ax 2＋bx ＋c ＝0有一个根是x ＝3IABC二、填空（每题3分，共18分） 11、如果式子31-+x x 有意义，则x 的取值范围是 。

某某海拉尔区第四中学2014届中考数学6月模拟试题温馨提示：1．本试卷共4页，满分120分. 考试时间110分钟.2．答卷前务必将自己的某某、考号、座位号、试卷类型（A 或B ）涂写在答题卡上；选择题答案选出后，请用2B 铅笔把答题卡上对应题目的答案标号（ABCD ）涂黑，字迹签字笔直接答在答题卡上.在试卷上作答无效.3．请将某某与考号填写在本试卷相应位置上. 4．考试结束，将试卷、答题卡和草纸一并交回.一、选择题（下列各题的四个选项中只有一个正确. 共12小题，每小题3分，共36分） 1．5-的倒数是A ．15-B ．5-C ．5D ．152．下列各式计算正确的是A ．222()a b a b +=+B ．842(0)a a a a ÷=≠C ．2(3)6a b ab ⨯-=-D ．437()a a -= 3．某物体的展开图如图所示，它的左视图为4．点A （-3，4）与点B （m ，n ）关于x 轴对称，则点B 的坐标为 A ．（-3, -4） B ．（-3,4）C ．（3, -4）D ．（3,4）5．化简2244xy yx x --+的结果是A ．2x x +B ．2x x -C ．2y x +D ．2y x - 6．某次器乐比赛共有11名选手参加且他们的得分都互不相同．现在知道这次比赛按选手得分由高到低的顺序设置了6个获奖名额．若已知某位选手参加这次比赛的得分，要判断他能否获奖，则在下列描述选手比赛成绩的统计量中，只需知道 A ．方差B ．平均数C ．众数D ．中位数7．若两圆的半径分别是3cm 和4cm ，圆心距为7cm ，则这两圆的位置关系是A ．B ．C ．D ．第3题图A ．内切B ．相交C ．外切D ．外离8．如果一次函数y kx b =+的图象经过第一象限，且与y 轴负半轴相交，那么 A ．0k >，0b >B ．0k <，0b < C ．0k >，0b <D ．0k <，0b >9．A 种饮料比B 种饮料单价少1元，小峰买了2瓶A 种饮料和3瓶B 种饮料，一共花了13元，如果设B 种饮料单价为x 元/瓶，那么下面所列方程正确的是A ．2(1)313x x -+=B ．2(1)313x x ++=C ．23(1)13x x ++=D ．23(1)13x x +-= 10．某校为举办“庆祝建党90周年”A ．1120人B ．80人C ．280人D ．400人11．在四X 完全相同的卡片上,分别画有圆、菱形、等腰三角形、等腰梯形,现从中随机抽取一X,卡片上的图形恰好是中心对称图形的概率是B A ．1B ．14C ．34D ．1212．矩形面积为4，长y 宽x 的函数，其函数图像大致是二、填空题（本题5个小题，每小题3分，共15分） 13．在函数1y 2x-=中，自变量x 的取值X 围是. 14．分解因式：22am am a -+.15．抛物线22y x =-向上平移一个单位后，得到的抛物线的解析式是 16．如图，点C 、D 在以AB 为直径的半圆上，120BCD ∠=︒，若2AB =，则弦BD 的长为.17．观察下列单项式：x -，22x ，33x -，44x ，……根据你发现的规律，第n 个单项式为.三、解答题（本题4个小题，每小题6分，共24分）ABCO 第16题DBA F DCE18．计算：011(32)4cos30123||--++--（）°19．解不等式组184 1.1x x x x ⎧-⎨+>-⎩-，≥,并求出它的整数解.20．小明和小亮用图中所示的转盘做游戏：分别转动转盘两次，若两次指针指向的数字之差（第一次数字减第二次的数字）大于或等于2，小明获 胜，否则小亮获胜（指针恰好指在等分线上时重新转动转盤）． （1）分别求出小明和小亮得分的概率；（2）你认为游戏是否公平？若公平，请说明理由.21．某中学九年级数学兴趣小组为测量校内旗杆高度，如图，在C点测得旗杆顶端A 的仰角为30°，向前走了6米到达D 点，在 D 点测得旗杆顶端A 的仰角为60°(测角器的高度不计). （1）AD =米；（2）求旗杆AB 的高度（结果保留1位小数，3 1.73≈）. 四、（本题7分）22．在本学期某次考试中，某校初二⑴、初二⑵两班学生数学成绩统计如下表：分数 50 60 70 80 90 100 人数二（1）班351631112二（2）班25112137请根据表格提供的信息回答下列问题：（1）初二⑴班平均成绩为_________分，初二⑵班平均成绩为________分，从平均成绩看两个班成绩谁优谁次？（2）二⑴班众数为________分，二⑵班众数为________分。