根轨迹定义及根轨迹方程
- 格式:pdf
- 大小:333.79 KB
- 文档页数:8

第四章根轨迹法4-1 根轨迹法的基本概念4-2 常规根轨迹的绘制法则4-3 广义根轨迹4-1 根轨迹法的基本概念一、根轨迹的概念根轨迹:系统中某个参数从零到无穷变化时,系统闭环特征根在s平面上移动的轨迹。
根指的是闭环特征根(闭环极点)。
根轨迹法是根据开环传递函数与闭环传递函数的关系,通过开环传递函数直接分析闭环特征根及系统性能的图解法。
K =0 s 1=0 s 2=-40 < K <1s 1 s 2为不等的负实根K =1s 1=-2 s 2=-21 < K < ∞s 1s2 实部均为-2由根轨迹可知:1)当K =0时,s 1=0,s 2=-1,这两点恰是开环传递函数的极点,同时也是闭环特征方程的极点.2)当0<K < 1 时,s 1,2都是负实根,随着k 的增长,s 1从s 平面的原点向左移,s 2从-1点向右移。
3) 当K = 1时, s 1,2= -2,两根重合在一起,此时系统恰好处在临界阻尼状态。
4) 1 <K <∞,s 1,2为共轭复根,它们的实部恒等于-2,虚部随着K 的增大而增大,系统此时为欠阻尼状态。
★在s平面上,用箭头标明K增大时,闭环特征根移动的方向,以数值表明某极点处的增益大小。
有了根轨迹图就可以分析系统的各种性能:(1)稳定性:根轨迹均在s的左半平面,则系统对所有K>0都是稳定的。
(2)稳态性能:如图有一个开环极点(也是闭环极点)s=0。
说明属于I型系统,阶跃作用下的稳态误差为0。
在速度信号V0t作用下,稳态误差为V0/K,在加速度信号作用下,稳态误差为∞。
(3)动态性能:过阻尼临界阻尼欠阻尼K越大,阻尼比ξ越小,超调量σ%越大。
由此可知:1、利用根轨迹可以直观的分析K的变化对系统性能的影响。
2、根据性能指标的要求可以很快确定出系统闭环特征根的位置;从而确定出可变参数的大小,便于对系统进行设计。
由以上分析知:根轨迹与系统性能之间有着密切的联系,但是,高阶方程很难求解,用直接解闭环特征根的办法来绘制根轨迹是很麻烦的。

根轨迹法一、定义:〈①〉()()()01111*0=+++=+∏∏==nj imi ip s z s Ks G 。
其中*K 为根轨迹增益。
开环放大倍数∏∏===nj jmi ipzKK 11*闭环特征方程的根随参数*K 而变化的轨迹,称为根轨迹。
其符合两个条件:()()()()⎪⎩⎪⎨⎧=∠+=∠=非最小相位系统或最小相位系统相角条件:幅值条件:,2,121000ππk s G k s G s G〈②〉几条规则:①实轴上的根轨迹〈最小相位系统〉右边有奇数个零极点时,有根轨迹 〈非最小相位系统〉右边有偶数个零极点时,有根轨迹 ②根轨迹条数=Max (n,m ),起点为开环极点(0=g K ),终点为开环零点(∞→g K )③渐进线条数:(n-m )条,与实轴交点坐标:mn --=∑∑零点极点1σ与实轴夹角:()mn k -+±=πϕ121。
④分离点与会合点:使0*=dsdK ,并使*K >0的点 ⑤复数极点出射角:∑∑-+︒=量辐角其他极点至该极点的向零点至极点的向量辐角1801p θ对非最小相位系统∑∑-='量辐角其他极点至该极点的向零点至极点的向量辐角1p θ 复数零点的入射角:∑∑+-︒=角极点至该零点的向量辐量辐角其他零点至该零点的向1801z θ对非最小相位系统∑∑+-='角极点至该零点的向量辐量辐角其他零点至该零点的向1z θ⑥与虚轴交点:(a )用劳斯判据确定,用辅助方程求得(b )ωj s =代入闭环特征方程,由实部=0,虚部=0求得例1:()()()210++=s s s Ks G解:渐进线(3条):()()10321-=--+-=σ,()πππϕ,3312=+±=k由()()0211=+++s s s K,则()()21++-=s s s K ,()()026323223*=++-=++-=s s dsss s d ds dK ,得 ⎩⎨⎧-=-==-=385.0,577.1385.0,423.0*22*11K s K s 与虚轴的交点:方法一02323=+++K s s s ,劳斯阵:Ks K sKs s 0123323021-要与虚轴有交点,则有一行全零,即6032=⇒=-K K辅助方程:j s s 20632,12±=⇒=+ 方法二将ωj s =代入特征方程:()()()02323=+++K j j j ωωω2,60320332==⇒=-=-ωωωωK K 虚部:实部:,则与虚部的交点6,22,1=±=K j s 根轨迹如下图例2:()()32220+++=s s s K s G 解:渐进线一条。








第四章根轨迹法(第一讲)根轨迹定义及根轨迹方程
引言
•分析和设计系统时确定闭环极点(即特征根)在复平面的位置是十分有意义的:
1)闭环系统的极点在复平面的位置决定了系统的稳定性;
2)系统的性能指标也主要由闭环极点的位置决定;•通过求解高阶代数方程确定闭环极点是困难的;
•闭环系统的极点与系统的参数有关,如开环增益等;•希望找到一种不用求解代数方程,就能确定当某个参数变化时极点的位置的方法。
•1948年伊文思(Walter R.Evans)提出了根轨迹法;•根轨迹方法能够确定当某个参数变化时,闭环极点在
特征方程2220
s s K ++=特征根1,2112s K =−±−120 0 2K s s ===−120.5 1
K s s ===−1,21 11K s j ==−±∞
±−=∞→j s K 1 2,1K 1
(0.51)s s +0-21
-1
j
-1根轨迹
K
1
(0.51)
s s+
根轨迹定义
根轨迹是指当系统开环的某个参数(如开环增益)从零变化到无穷大时,闭环特征方程的根在复平面上移动的轨迹。
0 -2
1
-1
j
-1
根据所绘制的根轨迹图可知:
K>0时,系统稳定;0<K<0.5时,过阻尼状态,
阶跃响应为单调衰减过程;
K=0.5时,临界阻尼状态,阶跃响应为单调衰减过程;K>0.5时,欠阻尼状态,
K 1
(0.51)
s s +0-21-1j
-1
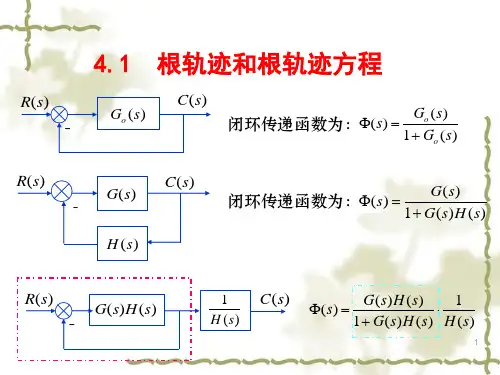
根轨迹方程)(s G ()
H s )(s R )
(s C 开环传递函数分别为开环零、极点;
i p j z 0K *≤<∞n m ≥为开环根轨迹增益,并假设。
特征方程0
)()(1=+s H s G 由于闭环极点就是特征方程的根,该方程又称为根轨迹方程。
1
1
()
()()()
m
j j n
i i s z G s H s K s p =*=−=−∏∏
j=11
||
1||
m
j n i i s z K s p *
=−=−∏∏π
)12()()(1
1+=−∠−−∠
∑∑==k p s z s n
i i m j j )(s G ()
H s )
(s R )
(s C 根轨迹方程可分解为模值方程和相角方程:11
()()()=1()
m
j j n
i i s z G s H s K s p =*=−=−−∏∏(1)由于,所以任何复数s 均满足模值方程;
(2)相角方程是确定复数s 是否为根轨迹上的点的充分必要条件;
0K *≤<∞
例4-1 已知单位负反馈系统的开环传递函数为
2
()(2)K
G s s *
=+试证明复平面上点是该系统的闭环极点。
1224, 24s j s j =−+=−−证明:该系统有两个开环极点:,无开环零点。
122p p ==−相角方程:2(2)(21)s k π−⋅∠+=+模值方程:22K s *=+j
1s 402−12(2)s π−∠+=−22(2)s π
−∠+=22
**。