状态空间分析方法基础

状态空间分析与设计状态空间分析与设计是系统工程与控制工程中常用的分析和设计方法。

它通过建立系统的状态空间模型，对系统的动态行为进行定性和定量分析，并在此基础上进行系统设计和优化。

本文将深入介绍状态空间分析与设计的相关概念、原理和应用。

一、状态空间分析与设计概述状态空间是系统在任意时刻的状态所组成的集合。

在状态空间中，系统的每个状态都可以由一组状态变量完全描述。

因此，状态空间分析与设计的核心是建立系统的状态方程和输出方程，并利用这些方程进行性能分析和控制器设计。

二、状态方程与输出方程状态方程描述了系统状态的演变规律。

它是一个一阶微分方程，用矩阵形式表示为：x' = Ax + Bu其中，x是状态向量，A是系统的状态转移矩阵，B是输入矩阵，u 是外部输入。

状态方程描述了系统状态变量随时间的变化规律，可以用来分析系统的稳定性、响应速度等性能指标。

输出方程描述了系统输出与状态之间的关系。

它是一个线性方程，用矩阵形式表示为：y = Cx + Du其中，y是输出向量，C是输出矩阵，D是直接传递矩阵。

输出方程可以用来分析系统的可控性和可观性，以及设计满足特定输出要求的控制器。

三、状态空间分析方法1. 稳定性分析利用状态方程，可以通过特征值分析判断系统的稳定性。

对于线性时不变系统，当所有特征值的实部小于零时，系统是稳定的。

通过分析系统的特征值，可以设计出稳定性更好的控制器。

2. 响应分析利用状态方程和输出方程，可以分析系统的响应特性。

包括阶跃响应、脉冲响应、频率响应等。

通过分析系统的响应，可以评估系统的性能，并设计出满足要求的控制器。

3. 控制器设计状态空间方法可以直接用于控制器设计。

常见的控制器设计方法包括状态反馈控制、最优控制和鲁棒控制等。

这些方法都是基于状态空间模型进行的，可以根据系统的要求选择合适的控制器设计方法。

四、状态空间分析与设计应用状态空间分析与设计在工程实践中得到广泛应用。

例如，它可以用于电力系统的稳定性分析和控制、飞行器的自动控制系统设计、机械振动控制等。

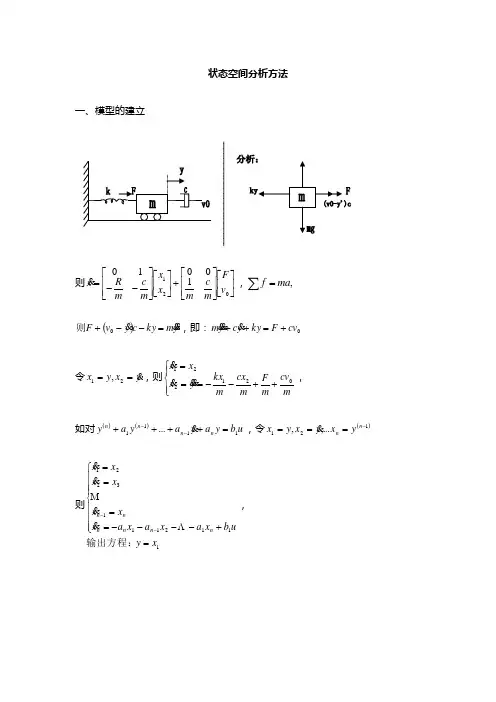
状态空间分析方法一、模型的建立则⎥⎦⎤⎢⎣⎡⎥⎥⎦⎤⎢⎢⎣⎡+⎥⎦⎤⎢⎣⎡⎥⎥⎦⎤⎢⎢⎣⎡--=02110010v F m cm x x m cmR x，,ma f =∑ ()y m ky c y v F =--+0则，即：0cv F ky y c ym +=++ 令y x y x ==21,，则⎪⎩⎪⎨⎧++--===m cv m Fm cx m kx y x x x021221，如对()()u b y a ya y a y n n n n 1111...=++++-- ，令()121,...,-===n n y x y x y x 则11121113221x y u b x a x a x a x x x x x x xn n n n n n =⎪⎪⎪⎩⎪⎪⎪⎨⎧+----====--输出方程：，或[]xy u b x a a ax n n 0010001001000010111=⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎣⎡+⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎣⎡---=-例1：由传递函数来求()()()()()s U s Q s U s Y a s a sa sb s b sb sb s G nn n n mm m m⋅=++++++++=----1111110 ，则 ()()nn n na s a sa s s U s Q ++++=--1111，()()m m mb s b sb s U s Y +++=-10()()[]()s Q a s a sa s U s Q s n n n n++-=--111则⎪⎪⎪⎩⎪⎪⎪⎨⎧----====--n n n n n n x a x a x a u xx x x x x x 121113221，即 []xb b b y u x a a axm m n n 00100010010000100111--=⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎣⎡+⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎣⎡---=例2：()()()()35222112167201742232+++++-=+++++==s s s s s s s s s U s Y s G ，有：⎪⎪⎩⎪⎪⎨⎧+-=+-=+-=+-=321332221152322x x x y u x x u x x x x x 即：[]⎪⎪⎩⎪⎪⎨⎧-=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡+⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡---=x y u x x 512110300020012 可见-2为重根，则此为约当标准型。

第九章状态空间分析方法第9章状态空间分析方法基本要求9-1 状态空间方法基础9-2 线性系统的可控性和可观性9-3 状态反馈和状态观测器9-4 有界输入、有界输出的稳定性9-5 李雅普诺夫第二方法引言：前面几章所学的内容称为经典控制理论；下面要学的内容称为现代控制理论。

两者作一简单比较。

经典控制理论(50年代前)现代控制理论(50年代后)研究对象单输入单输出的线性定常系统可以比较复杂数学模型传递函数(输入、输出描述)状态方程(可描述内部行为)数学基础运算微积、复变函数线性代数、矩阵理论设计方法的特点非唯一性、试凑成份多, 经验起很大作用。

主要在复数设计的解析性，与计算机结合，主要在时间域进行。

基本要求①掌握由系统输入—输出的微分方程式、系统动态结构图、及简单物理模型图建立系统状态空间模型的方法。

②熟练掌握矩阵指数的计算方法，熟练掌握由时域和复数域求解状态方程的方法。

熟练掌握由动态方程计算传递函数的公式。

③正确理解可逆线性变换, 熟练掌握可逆线性变换前、后动态方程各矩阵的关系。

④正确理解可控性和可观测性的概念，熟练掌握和运用可控性判据和可观性判据。

⑤熟练掌握可逆线性变换矩阵的构成方法, 能将可控系统化为可控标准形。

能将不可控系统进行可控性分解。

⑥正确理解对偶原理, 会将原系统的有关可观测性的问题转化为对偶系统的可控性问题来研究。

⑦正确理解单变量系统零、极点对消与动态方程可控、可观测的关系。

熟练掌握传递函数的可控性标准形实现、可观性标准形实现的构成方法。

⑧正确理解状态反馈对可控性，可观性的影响, 正确理解状态反馈可任意配置闭环极点的充要条件。

⑨熟练掌握全维状态观测器的公式和设计方法, 熟练掌握由观测器得到的状态估计值代替状态值构成的状态反馈系统, 可进行闭环极点配置和观测器极点配置。

⑩正确理解系统齐次方程渐近稳定和系统BIBO稳定的概念, 熟练掌握判别渐近稳定的方法和判别系统BIBO稳定的方法。

11正确理解李雅普诺夫方程正定对称解存在的条件和解法, 能通过解李雅普诺夫方程进行稳定性分析。

线性系统状态空间分析和运动解状态空间分析方法是一种用来描述线性系统的分析方法。

它将系统的动态特性用一组状态变量来表示，并通过矩阵形式的状态方程进行分析和求解。

状态空间方法是目前广泛应用于自动控制系统设计与分析的一种方法，它可以对系统的稳定性、可控性、可观性以及性能等进行定量分析。

在状态空间分析方法中，首先需要将系统的微分方程表示为矩阵形式的状态方程。

状态方程描述了各个状态变量和它们的变化率之间的关系。

假设系统有n个状态变量x1, x2, ..., xn和m个输入变量u1, u2, ..., um，状态方程可以表示为:dx/dt = Ax + Bu其中，dx/dt是状态变量的变化率，A是状态矩阵，描述状态变量之间的耦合关系，B是输入矩阵，描述输入变量对状态变量的影响。

状态空间分析方法的基本思想是将系统转化为状态空间表达式，然后通过对状态方程进行分析和求解来得到系统的特性和响应。

常见的分析方法包括对系统的稳定性、可控性和可观性进行评估。

稳定性是系统的基本性质之一，用来描述系统在受到扰动时是否能够恢复到平衡状态。

在状态空间方法中，通过研究系统的特征根（或特征值）可以判断系统的稳定性。

特征根是状态方程的解的根，系统的稳定性与特征根的实部有关。

如果特征根的实部都小于零，则系统是稳定的；如果特征根存在实部大于零的情况，则系统是不稳定的。

可控性是指系统是否可以通过输入变量来控制系统的状态变量。

在状态空间方法中，通过可控性矩阵来判断系统的可控性。

如果可控性矩阵的秩等于系统的状态变量个数，则系统是可控的；如果可控性矩阵的秩小于系统的状态变量个数，则系统是不可控的。

可观性是指系统的状态变量是否可以通过观测变量来测量得到。

在状态空间方法中，通过可观性矩阵来判断系统的可观性。

如果可观性矩阵的秩等于系统的状态变量个数，则系统是可观的；如果可观性矩阵的秩小于系统的状态变量个数，则系统是不可观的。

除了稳定性、可控性和可观性外，状态空间分析方法还可以用来分析系统的性能指标，如系统的响应时间、稳态误差和系统的最大误差等。

控制系统的状态空间分析方法控制系统是指将输入信号进行处理，通过执行特定的控制算法，使系统输出信号满足特定要求的系统。

控制系统有多种形式，例如电子系统、机械系统、化学系统、热系统等等。

控制系统的设计和分析是一个复杂的过程，需要考虑多个因素，包括系统动态响应、稳定性、鲁棒性、控制器的性能指标等等。

控制系统的状态空间表示是一种广泛应用的分析方法。

状态空间表示是将系统的状态和状态方程用矩阵和向量的形式表示出来。

状态方程是一组描述系统动态响应的微分方程或差分方程。

状态空间表示可以描述线性系统和非线性系统。

对于线性系统，状态空间表示为：dx/dt = Ax + Buy = Cx + Du其中，x是状态向量，表示系统的内部状态，u是输入向量，表示外部输入，y是输出向量，表示系统响应，A、B、C、D是矩阵，分别表示状态方程中的系数。

状态空间表示的优点在于它可以提供系统的完整信息，包括系统的结构和动态特性。

通过状态空间表示可以计算系统的传递函数、频率响应、控制器设计等等。

状态空间表示的另一个优点在于它可以用于多变量控制和非线性控制。

在多变量控制中，状态空间表示可以直接描述多变量系统的动态特性和相互关系。

在非线性控制中，状态空间表示可以近似描述非线性系统的动态行为，从而进行控制器设计。

状态空间分析方法是指基于状态空间表示进行系统分析的方法。

常见的状态空间分析方法包括状态转移矩阵法、观测矩阵法、极点配置法、模型匹配法等等。

状态转移矩阵法是指根据系统的状态方程，计算系统状态随时间的演变。

状态转移矩阵可以用于计算系统的传递函数、频率响应等等。

观测矩阵法是指根据系统的状态方程和输出方程，计算系统的状态和输出之间的关系。

观测矩阵可以用于设计状态反馈控制器和观测器。

极点配置法是指根据系统的状态方程和性能指标，设计状态反馈控制器，使系统的极点满足指定的要求。

极点配置法可以用于设计稳定控制器和提高系统的性能指标。

模型匹配法是指通过拟合实验数据或理论模型，确定系统的状态方程和性能指标。

第二章状态空间分析法2－1 状态、状态变量、状态空间、状态方程、动态方程任何一个系统在特定时刻都有一个特定的状态，每个状态都可以用最小的一组(一个或多个)独立的状态变量来描述。

设系统有n个状态变量x1，x2，…，x n，它们都是时间t的函数，控制系统的每一个状态都可以在一个由x1，x2，…，x n为轴的n维状态空间上的一点来表示，用向量形式表示就是:X = (x1，x2，…，xn)TX称作系统的状态向量。

设系统的控制输入为：u1，u2，...，u r，它们也是时间t的函数。

记：U = (u1，u2，...，ur)T那么表示系统状态变量X(t)随系统输入U(t)以及时间t变化的规律的方程就是控制系统的状态方程，如式（2－1）所示。

………………………………………………………………（2－1）其中F = (f1，f2，...，f n)T是一个函数矢量。

设系统的输出变量为y1，y2，...，y m，则Y = (y1，y2，...，y m)T 称为系统的输出向量。

表示输出变量Y(t)与系统状态变量X(t)、系统输入U(t)以及时间t的关系的方程就称作系统的输出方程，如式2－2所示。

…………………………………………………………. (2－2)其中G = (g1，g2，...，g m)T是一个函数矢量。

在现代控制理论中，用系统的状态方程和输出方程来描述系统的动态行为，状态方程和输出方程合起来称作系统的状态空间表达式或称动态方程。

根据函数向量F和G的不同情况，一般控制系统可以分为如下四种：∙线性定常(时不变)系统（LTI-Linear Time Invariant）；∙线性不定常(时变)系统；∙非线性定常系统；∙非线性时变系统。

在本课程中，我们主要考虑线性定常系统(LTI)。

这时，系统的动态方程可以表示如下：…………….（2－3）………………（2－4）写成矢量形式为：……………………………………………………………………………（2－5）上式中，A nxn称为系统矩阵，B nxr称为输入(或控制)矩阵。

状态空间分析法一、内容概要《状态空间分析法》是一篇介绍状态空间理论及其应用的分析文章。

本文首先简要概述状态空间分析法的概念及其相关领域的研究背景。

接着阐述状态空间分析法的理论基础，包括其基本原理、数学工具以及相关技术的理论基础。

然后介绍状态空间分析法在不同领域中的应用实例，包括物理系统、控制系统、信号处理、通信系统等领域的应用情况。

文章还将探讨状态空间分析法的优势与局限性，以及未来可能的发展方向和潜在应用。

对全文进行总结，强调状态空间分析法在科学研究、工程实践等领域的重要性和价值。

1. 介绍状态空间分析法的概念及其在工程、科学、经济等领域的应用状态空间分析法是一种强大的数学工具，广泛应用于工程、科学和经济等多个领域。

本文将详细介绍状态空间分析法的概念及其在各个领域的应用。

状态空间分析法是一种以系统状态为研究对象的数学分析方法。

它以系统的状态变量为核心，通过对状态变量的描述和分析，揭示系统的行为模式和内在规律。

状态空间分析法通过构建状态空间模型，将复杂的系统问题转化为数学模型，便于进行理论分析和数值计算。

在状态空间中，系统的状态可以通过一系列的状态变量来描述，这些状态变量随时间变化，反映了系统的动态行为。

工程领域：在控制工程、信号处理等领域中，状态空间分析法被广泛应用于分析和设计动态系统。

通过构建系统的状态空间模型，可以方便地分析系统的稳定性、响应特性和控制性能。

此外状态空间分析法还可以用于故障诊断和系统识别等领域。

科学领域：在物理学、生物学和医学等自然科学领域，状态空间分析法同样发挥着重要作用。

例如在量子力学和电路分析中，系统的状态可以通过状态空间模型来描述，从而揭示系统的内在规律和特性。

此外在生物医学信号处理中，状态空间分析法也被广泛应用于生物电信号的分析和处理。

经济领域：在经济和金融领域，状态空间分析法被用于分析和预测经济系统的动态行为。

通过构建经济模型的状态空间表示，可以分析经济增长、市场波动和金融风险等问题，为经济决策提供支持。