冲激响应求解举例

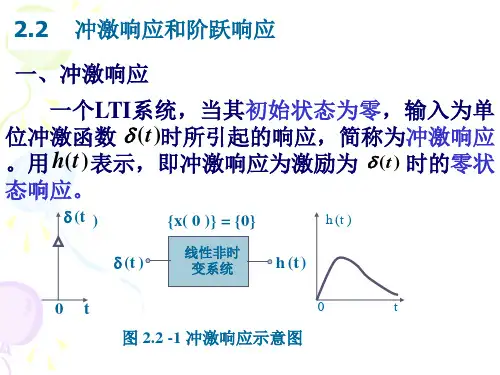
§2.3 冲激响应和阶跃响应通信与信息工程学院江帆系统在单位冲激信号作用下产生的零状态响应，称为单位冲激响应，简称冲激响应，一般用h (t )表示。

一．冲激响应)(t δ)(t h 1．定义)(t δh(t)=T[{0},δ(t)]例2-3-1描述某系统的微分方程为y”(t)+5y’(t)+6y(t)=f(t)求其冲激响应h(t)。

根据h(t)的定义有h”(t) + 5h’(t) + 6h(t) = δ(t)h’(0-) = h(0-) = 0先求h’(0+)和h(0+)。

因方程右端有δ(t)，故利用系数平衡法。

h”(t)中含δ(t)，h’(t)含ε(t)，h’(0+)≠h’(0-)，h(t)在t=0连续，即h(0+)=h(0-)。

积分得[h’(0+) -h’(0-)] + 5[h(0+) -h(0-)] + 6 = 1∫+−00)(dt t h考虑h(0+)= h(0-)，由上式可得h(0+)=h(0-)=0 , h’(0+) =1 + h’(0-) = 1对t>0时，有h”(t) + 5h’(t) + 6h(t) = 0故系统的冲激响应为一齐次解。

微分方程的特征根为-2，-3。

故系统的冲激响应为h(t)=(C1e-2t + C2e-3t)ε(t)代入初始条件求得C1=1,C2=-1, 所以h(t)=( e-2t-e-3t)ε(t)例2-3-1续例2-3-2描述某系统的微分方程为y”(t)+5y’(t)+6y(t)= f”(t) + 2f’(t) + 3f(t)求其冲激响应h(t)。

根据h(t)的定义有h”(t) + 5h’(t) + 6h(t) = δ”(t)+ 2δ’(t)+3δ(t) (1)h’(0-) = h(0-) = 0先求h’(0+)和h(0+)。

由方程可知，h(t) 中含δ(t)故令h(t) = aδ(t) + p1(t) [p i(t) 为不含δ(t) 的某函数] h’(t) = aδ’(t) + bδ(t) + p2(t)h”(t) = aδ”(t) + bδ’(t) + cδ(t)+ p3(t)代入式(1)，有aδ”(t) + bδ’(t)+ cδ(t) + p3(t) + 5[aδ’(t) + bδ(t) + p2(t) ] + 6[aδ(t) + p1(t) ] = δ”(t)+ 2δ’(t)+3δ(t)整理得aδ”(t)+(b+5a)δ’(t)+(c +5b+6a)δ(t) + p3(t)+5 p2(t)+6 p1(t) = δ”(t) + 2δ’(t) + 3δ(t)利用δ(t) 系数匹配，得 a =1 ，b = -3，c = 12所以h(t) = δ(t) + p1(t) （2）h’(t) = δ’(t) -3δ(t) + p2(t) （3）h”(t) = δ”(t) -3 δ’(t) + 12δ(t)+ p3(t) （4）对式(3)从0-到0+积分得h(0+) –h(0-) = –3对式(4)从0-到0+积分得h’(0+) –h’(0-) =12故h(0+) = –3，h’(0+) =12微分方程的特征根为–2，–3。

用冲激函数匹配法求冲激响应一、引言冲激响应是线性时不变系统的重要特性之一，它描述了系统在接受一个单位冲激信号时的输出响应。

在信号处理、控制系统等领域中，冲激响应的求解是非常重要的问题。

本文将介绍一种常用的方法——冲激函数匹配法，用于求解线性时不变系统的冲激响应。

二、冲激函数匹配法原理1. 线性时不变系统首先，我们需要明确什么是线性时不变系统。

线性时不变系统是指其输入与输出之间存在线性关系，并且其特性参数（如增益、相位等）与时间无关。

这类系统可以用微分方程或差分方程来描述。

2. 冲激函数接着，我们需要介绍什么是冲激函数。

在信号处理中，冲激函数通常指单位冲击函数，记作δ(t)。

它满足以下条件：$$\int_{-\infty}^{+\infty}\delta(t)dt=1$$$$\delta(t)=0, t\neq 0$$$$\int_{-\infty}^{+\infty}f(t)\delta(t-t_0)dt=f(t_0)$$其中第三个条件称为采样定理。

3. 冲激响应对于一个线性时不变系统，其冲激响应h(t)定义为其接受单位冲激信号δ(t)后的输出响应。

即：$$h(t)=\int_{-\infty}^{+\infty}\delta(\tau)x(t-\tau)d\tau$$其中x(t)为输入信号。

4. 冲激函数匹配法冲激函数匹配法是一种常用的求解线性时不变系统冲激响应的方法。

其基本思想是将输入信号x(t)表示为若干个单位冲击函数的线性组合，然后利用线性时不变系统的可叠加性质，将每个单位冲击函数的输出响应相加得到总的输出响应。

具体而言，设输入信号x(t)可以表示为：$$x(t)=\sum_{k=-\infty}^{+\infty}a_k\delta(t-kT)$$其中T为采样周期，a_k为系数。

则有：$$h(t)=\sum_{k=-\infty}^{+\infty}a_kh_k(t)$$其中h_k(t)为系统接受单位冲击函数δ(kT)后的输出响应。

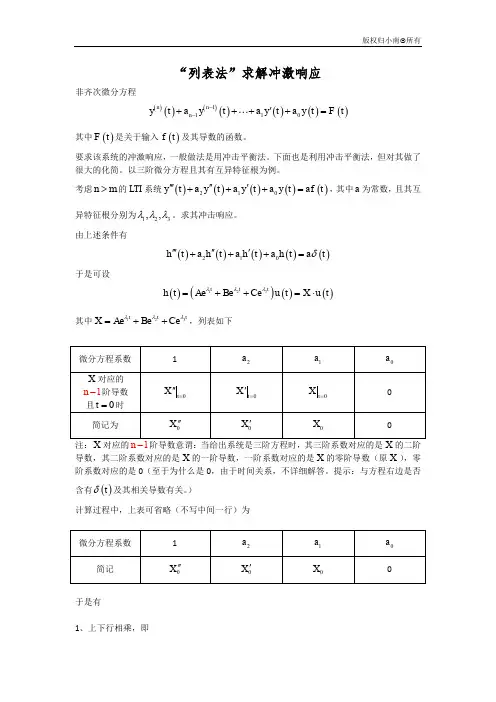
“列表法”求解冲激响应非齐次微分方程()()()()()()()1110n n n y t a y t a y t a y t F t --'++++=其中()F t 是关于输入()f t 及其导数的函数。

要求该系统的冲激响应，一般做法是用冲击平衡法。

下面也是利用冲击平衡法，但对其做了很大的化简。

以三阶微分方程且其有互异特征根为例。

考虑n m >的LTI 系统()()()()()210y t a y t a y t a y t af t ''''''+++=，其中a 为常数，且其互异特征根分别为123,,λλλ。

求其冲击响应。

由上述条件有()()()()()210h t a h t a h t a h t a t δ''''''+++=于是可设()()()()312t t t h t Ae Be Ce u t X u t λλλ=++=⋅其中312t ttX Ae Be Ce λλλ=++，列表如下注：对应的阶导数意谓：当给出系统是三阶方程时，其三阶系数对应的是的二阶导数，其二阶系数对应的是X 的一阶导数，一阶系数对应的是X 的零阶导数（原X ），零阶系数对应的是0（至于为什么是0，由于时间关系，不详细解答。

提示：与方程右边是否含有()t δ及其相关导数有关。

）计算过程中，上表可省略（不写中间一行）为于是有1、上下行相乘，即2010X a X a X a '''++= （其中a 为()t δ即()f t 的系数）200X a X '+= （其中0为()t δ'即()f t '的系数，此处为0，当方程右边出现()k t δ'时，即为其系数k 。

这里可在第二行末尾补任意位零，则0a 斜乘0，忽略不写）00X = （其中0为()t δ''即()f t ''的系数，即为0，同上）注：当方程三阶时，得到了三个方程，否则继续斜乘（第二行不足则在末尾补零），直到最高阶系数乘上方程零阶导数的系数0a 对应的数（在n m >的情况下为0）。