信号与系统冲激响应求解举例

格式：ppt
大小：344.50 KB
文档页数：5

下载文档原格式

/ 5

系统函数和冲激响应的关系

系统函数和冲激响应的关系
系统函数和冲激响应是信号处理中常用的概念。

系统函数是指输入信号和输出信号之间的关系，通常用传递函数或频率响应函数来描述。

而冲激响应是指当输入信号为单位脉冲函数时，系统的输出响应。

系统函数和冲激响应之间的关系可以通过傅里叶变换来描述。

具体来说，系统函数和冲激响应的傅里叶变换是互为倒数的关系，即系统函数的傅里叶变换是冲激响应的倒数，而冲激响应的傅里叶变换是系统函数的倒数。

这个关系可以用数学公式表示为：
H(f) = Y(f) / X(f)
其中，H(f)表示系统函数的傅里叶变换，Y(f)表示输出信号的傅里叶变换，X(f)表示输入信号的傅里叶变换。

如果输入信号为单位脉冲函数，即X(f)等于1，那么有：
H(f) = Y(f)
也就是说，系统函数的傅里叶变换等于冲激响应的傅里叶变换。

这个关系的物理意义是，系统函数描述了一个系统对于任意输入信号的响应特性，而冲激响应则揭示了系统对于一个单位脉冲信号的响应特性。

通过系统函数和冲激响应的关系可以推导出系统对于任意输入信号的响应，这是信号处理中重要的基本原理之一。

连续时间LTI系统的冲激响应

A (t) + 3B (t) B '(t) 2 (t) '(t)
解得A= －1, B =1
h(t) e3tu(t) (t)
可见冲激响应的形式要根据微分方程情况设定
2. 冲激响应的求解
连续时间LTI系统的冲激响应h(t)满足微分方程
h(n)(t)
a h (n1) n 1
(t)
a h ' (t) 1
a n 1h (n1) (t)
a h ' (t) 1
a 0h ( t )
bm (m) (t)
b m 1 ( m 1 ) ( t )
b 1
'(t)
b (t) 0
2. 冲激响应的求解
[例] 某线性时不变系统的微分方程为y'(t) 3y(t) 2x(t), t 0 试求系统的冲激响应h(t)。
i1
j0
由微分方程的特征根确定u(t)前的指数形式。
由微分方程 (t)的最高阶导数与h(t)的最高阶导数确定 (j)(t)项。
连续时间LTI系统的冲激响应
谢谢
本课程所引用的一些素材为主讲老师多年的教学积累，来源于多种媒体及同事、同行、朋友的交流，难以一一注明出处，特此说明并表示感谢！
a 0h ( t )
bm
(m)
(t)
b
b 1
'(t) b0 ( t )
(1) 当 n>m 时(假设特征根为不等实根)
n
h(t) ( Kiesit )u(t)
i1
(2) 当nm 时, h(t)应含有冲激及其高阶导数
n
mn
h(t) ( Kiesit )u(t) Aj ( j) (t)
i1

《信号与系统》中冲激函数δ(t)的教学探讨

《信号与系统》中冲激函数δ(t)的教学探讨作者：陈光红来源：《电脑知识与技术》2011年第25期摘要：通过对冲激函数δ(t)的工程定义、性质及由其引起的冲激响应h(t)等的分析，举例说明了与冲激函数相关的知识点及在运用时需注意的问题，并用三种方法求解冲激响应。

关键词：冲激函数δ(t)；冲激响应h(t)；傅立叶变换；拉普拉斯变换中图分类号：G642文献标识码：A文章编号：1009-3044(2011)25-6264-02Teaching Discussion of Dirac Delta Function in Information and SystemCHEN Guang-hong(Department of Electronic Information Engineering, Suzhou Vocational University, Suzhou 215104, China)Abstract: Definition and property of Dirac delta function is analyzed. Impulse response caused by Dirac delta function is introduced. Some examples are used to explain the notice. Three methods are used to solve the impulse response.Key words: Dirac delta function; impulse response; Fourier transform; Laplace transform信号与系统是通信技术和电子信息技术专业的一门核心课程。

冲激函数δ(t)是信号与系统中的重要信号，此信号本身有采样性质、偶对称性质等，由其衍生出的卷积性质、冲激响应等都是信号与系统中的重要知识点。

信号与系统零状态响应求解及系统全响应分析

⏹经典法⏹双零法☐零输入响应☐零状态响应⏹变换域法特征方程→特征根→含待定系数的齐次解→由初始条件(0-)→零输入响应方法①：先求解冲激响应h(t)，再计算零状态响应h(t)*f(t) 。

方法②：将输入信号等效为某虚拟系统的冲激响应，然后求解系统和虚拟系统的总响应，得到零状态响应。

单位冲激响应(复习)()()n n m m n m m p a p a p a h t b p b p b p b t −−−−++++=++++11110110()()δ h(t ) 的表达式：①与特征根有关当为无重根单根形式时有：①与n,m相对大小有关●当n > m 时，h (t )中不含δ(t )及其各阶导数●当n=m 时，h (t )中应包含δ(t )●当n < m 时，h (t )中应包含δ(t )及其各阶导数1(?)()k nt k k h A e u t t λ=⎡⎤=⎢⎥⎣⎦+∑零输入/零状态的求解方法；全响应分析零输入/零状态的求解方法；全响应分析1.掌握零输入/零状态响应的求解方法2.掌握系统的全响应模式方法一（掌握）：卷积法求解，在求解冲激响应的基础上，利用卷积求解。

双零法零输入特征方程→特征根→含待定系数的齐次解→由0-时刻的初始条件计算系数求解冲激响应，通过卷积计算任意输入信号的响应零状态零状态()f t()()*()fy t f t h t=零状态响应5、零状态响应的求解初始状态为零时，输出y(t)完全由输入f(t)决定，此时y(t)=yf(t)。

零状态响应可以由三种方法得到。

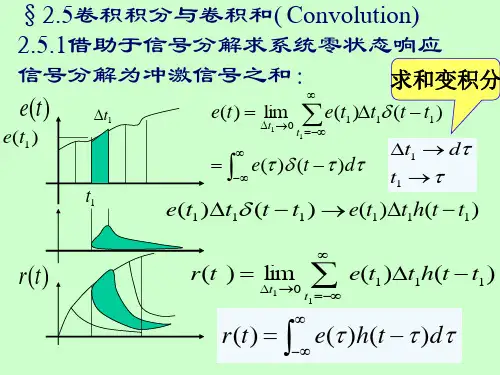
()i h t τ−()i t δτ−时不变()()i i i f t ττδτΔ−(())i i i h t f τττΔ−线性()()i i i i f t ττδτ∞=−∞Δ−∑可加性()()i i i i h t f τττ∞=−∞−Δ∑i i i idt τττττΔ→Δ连续变化（0），用代替,并用替换()()f t d τδττ∞−∞−⎰)(()f d h t τττ∞−∞−⎰线性时不变()()()f t d f t τδττ∞≡−=⎰()()()==h t f t y t ∗零状态卷积法的由来：LTI系统的性质5、零状态响应的求解卷积法求解零状态响应：线性时不变系统的性质若系统为因果系统, 即h (信号，则有0(()(tf t f h τ⎰方法二（熟练掌握）：将输入信号f (t )看做某个系统的冲激响应的，此时f (t )通过系统的响应等于：①冲激信号经过h 1(t )=f (t )的系统②再通过冲激响应为h (t )的系统的响应③列写h all (t )=f (t )*h (t )的算子方程④利用2.6中冲激响应求解法得h all (t )，即有y f (t )=h all (t )()f t ()()*()f y t f t h t =零状态()f t all ()()*()h t f t h t =5、零状态响应的求解零状态()f t ()()*f y t f t =零状态响应非常重要：①系统分析的大问题；②概念容易混淆。

系统的零状态响应=激励与系统冲激响应的卷积

h(t)
单位样值响应h(n)：
（n）
hБайду номын сангаасn)
（1）零状态响应响应（2）具有零输入响应的
形式
（3）反映系统本身特性因果性稳定性
（4）根据框图求h(t),h(n)
3 卷积定义 ( Convolution)
r(t) e(t) h(t) e( )h(t )d
系统的零状态响应＝激励与系统冲激响应的卷积
f (n)
推广： f (n)* (n n1) (n n1)* f (n) f (n n1)
f (n n1)* (n n2 ) (n n1)* f (n n2 ) f (n n1 n2 )
二、卷积和的图解说明
f (n) f1(n) f2 (n) f1(k ) f2 (n k )
t
t
f1() * f2 ()d f1() * f2 ()d
t
f2 () * f1()d
类似地：对高阶导数和积分
f (t) f1(t) * f2(t)
则：
f
(i ) (t)
f1( j) (t) *
f
(i 2
j
)
(t)
其中，I，j取正整数时，为导数阶次若I，j取负整数时，为重积分次数，如
r(t) e( )h(t )d
e(t)
lim
t1 0
e(t1)t1
t1
(t
t1)
卷积的物理含义图解：
k (t t1)
kh(t t1)
A
e(t1)t1 (t t1)
A
e(t1)t1h(t t1)
LTI系统的性质
e(t)为激励系统的零状态响应
r(t
) lim t10 t1

matlab求冲激响应和阶跃响应数值解

matlab求冲激响应和阶跃响应数值解标题：深度探讨matlab求冲激响应和阶跃响应数值解的方法一、前言在信号与系统课程中，我们经常会遇到需要求解系统的冲激响应和阶跃响应的问题。

而在实际工程实践中，我们往往需要利用计算机进行数值求解。

在本文中，我们将重点探讨如何利用matlab对系统的冲激响应和阶跃响应进行数值求解，并结合个人观点，深入探讨其中的数学原理和工程应用。

二、matlab求解冲激响应的数值解1. 离散系统的冲激响应在信号与系统中，我们经常会遇到离散系统的冲激响应求解问题。

离散系统的冲激响应可以通过卷积求解，而在matlab中，我们可以利用conv函数来进行计算。

具体来说，在matlab中，我们可以定义系统的传递函数H(z)，然后利用impulse函数生成单位脉冲输入序列，再利用conv函数与传递函数H(z)进行卷积运算，即可得到离散系统的冲激响应序列。

2. 个人观点与实践应用对于离散系统的冲激响应，我个人认为在实际工程中，常常需要对数字滤波器进行设计和分析。

而利用matlab求解冲激响应可以帮助工程师们更好地理解数字滤波器的特性，从而进行参数调整和性能优化。

三、matlab求解阶跃响应的数值解1. 连续系统的阶跃响应在连续系统中，阶跃响应是指系统在接受单位阶跃输入后的响应。

在matlab中，我们可以利用step函数来求解连续系统的阶跃响应。

具体来说，我们可以利用tf函数定义连续系统的传递函数G(s)，然后利用step函数对系统进行仿真，即可得到连续系统的阶跃响应曲线。

2. 个人观点与实践应用对于连续系统的阶跃响应，我认为在控制系统工程中具有重要的应用价值。

控制系统工程师们往往需要对系统的阶跃响应进行分析和优化，而利用matlab进行阶跃响应的数值求解，可以帮助工程师们更好地理解系统的动态特性，从而提高系统的稳定性和性能。

四、总结与回顾通过对matlab求解冲激响应和阶跃响应的数值解的深入探讨，我们不仅对系统的动态特性有了更深入的理解，同时也学会了如何利用matlab来进行系统动态特性的数值分析。

系统函数及冲激响应

6W
和电感两端电压uL (t ) 。
1H uL(t ) 2W
1W
-
2
2 +
UL(s)
Li
L
(0
-
-)
-
+
+ uC (t )
iL(0- )
s
uC (0- ) + s-
+
(1) iL (0- ) = 0.5 A ，uC (0- ) = 2V
5 s
UC (s)
2
IL(s)
=
uC
(0s
)
+
LiL (0-
)
2+2+2+ 5+s
§4.5 系统函数与冲激响应
主要内容系统函数 LTI互联的系统函数
并联级联反馈连接
重点系统函数
《信号与系统》 BUPT EE
难点反馈连接
结束开始
课前练习
2W 2W t = 0
+
图示电路，开关动作前已进入稳态， 2W 试求开关打开后电感支路电流iL (t )
uC (t ) -
+
1F + 5 4V -
3.系统函数的求法
(1) h(t) H(s)
(2)零状态下，由s域电路模型，列s域方程，
H(s)
=
R(s) E(s)
(3)设输入为(t)，零状态下微分方程两端取拉氏变换
H(s)
=
R(s) E(s)
退出
4.例题
给定系统微分方程：
d
2r(t dt 2
)
+
5
dr(t dt
)
+

信号与系统冲激响应和阶跃响应

r t
t2
t
t
a t a t
b
bu
t t
c
u
t
rt aut
h 0 1 ,h '0 2
代入h(t),得
hh'00A A113AA2212
h(t)1ete3t u(t)
A A121212
2
X
12
第
用奇异函数项相平衡法求待定系数页
h ( t ) A 1 e t A 2 e 3 tu ( t )
RC (t)A (t)
1 RCA1 A
RC
X
波形
htvC(t)R 1C eR 1C tu(t)
vC (t) h(t) 1 RC
iC(t)
CdvC(t) dt
O
注意！
iC (t)
R12CeR1Ctu(t)
1 (t)
R
1
O R
电容器的电流在
t =0时有一冲激，这就是电容电压突
1 R 2C
变的原因。
•当nm时， ht中应包 t含；
•当nm时， ht应包含 t及其各阶导数。 X
10
第
例2-5-2 页
求系统 d d 2r t(2 t)4d d r(tt)3 r(t)的冲d d e 激(tt响) 应2 e 。(t) 解：
将e(t)→(t)， r(t)→h(t)
d 2 d h t( 2 t) 4d d h (tt)3 h (t)d d ( tt)2 (t)
CtR1CeR1Ctut
X
6
方法2：奇异函数项相平衡原理
第页
已知方程冲激响应求导代入原方程
RC dvdCt(t)vC(t)(t) t vC(t)Ae RCu(t)

2.2 冲激响应和阶跃响应

求其冲激响应h(t)。
■
第5页
冲激响应求解举例1
例1 描述某系统的微分方程为
y”(t)+5y’(t)+6y(t)= f”(t) + 2f’(t) + 3f(t)
求其冲激响应h(t)。
解根据h(t)的定义有
h”(t) + 5h’(t) + 6h(t) = δ”(t)+ 2δ’(t)+3δ(t) (1)
对式(4)从0-到0+积分得 h’(0+) – h’(0-) =12
故 h(0+) = – 3， h’(0+) =12
▲
■
第7页
对t>0时，有 h”(t) + 5h’(t) + 6h(t) = 0
微分方程的特征根为– 2， – 3。故系统的冲激响应为 h(t)= C1e–2t + C2e–3t ， t>0
h0 1 , h' 0 2
代入h(t)，确定系数C1,C2，得
h(t) 1 (et e3t ) (t)
2
▲
■
第 12 页
法二：用奇异函数项相平衡法求待定系数
h(t) C1et C2e3t (t)
h (t) C1et C2e3t (t) C1et 3C2e3t (t) C1 C2 (t) C1et 3C2e3t (t)
hn(t) an1hn1(t) a1h1(t) a0h(t)
bm m(t) bm1 m1(t) b1 1(t) b0 (t)
▲
■
第3页
• h(t)解答的形式
由于(t)及其导数在 t≥0+ 时都为零，因而方程式右端
的自由项恒等于零，这样原系统的冲激响应形式与齐次解的形式相同。 ①与特征根有关

信号与系统公式总结

信号与系统公式总结信号与系统是电子工程、通信工程、自动控制等领域中的重要基础课程，它研究了信号的传输、处理以及系统的行为特性。

在学习信号与系统的过程中，我们需要掌握一些基本的数学公式，以便更好地理解和分析信号与系统的特性。

本文将对信号与系统中常用的公式进行总结和归纳，以帮助读者更好地掌握和应用。

一、信号的表示在信号与系统中，我们常常遇到时域信号、频域信号和复域信号。

它们分别通过不同的数学表示方法来描述。

1. 时域信号时域信号使用时间作为自变量进行描述，常用的时域信号表示方法有：- 脉冲函数（Impulse Function）:δ(t)是一个函数，当t=0时取值为无穷大，其他时刻取值为零，即δ(t) = ∞，t = 0；δ(t) = 0，t ≠ 0。

- 阶跃函数（Step Function）:u(t)是一个函数，当t≥0时取值为1，t<0时取值为0。

- 矩形函数（Rectangular Pulse）:rect(t/T)是一个函数，在|t| < T/2时取值为1，其他时刻取值为零。

2. 频域信号频域信号使用频率作为自变量进行描述，常用的频域信号表示方法有：- 正弦函数（Sine Function）:f(t)=A*sin(2πft+φ)是一个函数，A为振幅，f为频率，φ为相位。

- 余弦函数（Cosine Function）:g(t)=A*cos(2πft+φ)是一个函数，A为振幅，f为频率，φ为相位。

- 脉冲函数的频谱：脉冲函数的频谱是一个常数，即频率的绝对值小于无穷大的所有频率分量都具有相同的幅度。

3. 复域信号复域信号使用复数表示，并且可以同时描述时域信息和频域信息。

常用的复域信号表示方法有：- 复指数函数（Complex Exponential Function）:x(t) = Ae^(2πft+jφ)，其中A为振幅，f为频率，φ为相位。

二、线性时不变系统在信号与系统中，线性时不变系统（LTI system）是一类重要的系统。

1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

h′ (t) = C1e−t + C2e−3t δ (t) + − C1e−t −3C2e−3t ε (t)
−t −3t 1 2 1 2
(
−t
−3t
1
2
1
2
1
2
将h(t ), h′(t ), h′′(t )代入原方程
(C1 + C2 )δ ′(t) + (3C1 + C2 )δ (t) + 0⋅ε(t) = δ ′(t) + 2δ (t)
代原程：入方 aδ ′ ( t ) + bδ ( t ) + r ( t ) + 4aδ ( t ) + 4r2 ( t ) + 3r3 ( t ) =δ '(t) +2δ (t) 1 a=1 b+4a=2 即 b=-2
■ 第 2页
d2 h( t ) = δ ′( t ) − 2 ( t ) + r ( t ) δ 1 2 dt d h( t ) =δ (t) + r (t) 2 dt h( t ) = r ( t ) 3
求特征根冲激响应
λ2 + 4λ + 3 = 0 ⇒λ1 = −1, λ2 = −3
n = 2, m = 1, n > m h(t )中不包含冲激项
带ε(t)
h(t) = (C1e + C2e
−t
−3t
)ε(t)
■ 第 1页
两种求待定系数方法：两种求待定系数方法：求0+法 •求
法一：求0+值确定系数
∴ h(0+ ) = 1 , h' (0+ ) = −2
代入h(t)，确定系数 1,C2，得，确定系数C 代入
1 −t −3t h(t) = (e + e )ε (t) 2
■ 第 3页
解法二：线性时不变性质法
求系统 dt 2 解：设h (t)满足简单方程 1 满足简单方程
d2 h1(t) d2 y(t) +4 d y(t) d f (t) + 3y(t) = + 2 f (t) dt dt
的冲激响应。的冲激响应。
h1(t) = C1e−t + C2e−3t ε (t)
(
dt 2
d h1(t) +4 + 3h1(t) = δ (t) dt
)
h1' (0+ ) = 1
h1(0+ ) = 0
将边界条件代入h 式将边界条件代入 1(t)式，解得 C1=1/2， C2=-1/2，， - ，
根据系数平衡，根据系数平衡，得
1 C1 + C2 = 1 C1 = 2 ⇒ 3C1 + C2 = 2 C = 1 2 2
1 −t −3t h(t) = e + e ε (t) 2
(
)
■
第 5页
1 −t −3t h1(t) = e − e ε (t) 2
(
)
则由系统的线性时不变特性
h(t) = dh1(t) 1 + 2h1(t) = e−t + e−3t ε (t) dt 2
(
)
■
第 4页
法三：用奇异函数项相平衡法求待定系数
h(t) = C1e−t + C2e−3t ε(t)
(
)
) ( ) = (C + C )δ (t) + (−C e −3C e )ε (t) h′′(t ) = (C + C )δ ′(t ) + (−C −3C )δ (t ) + (C e + 9C e )ε(t )
冲激响应求解举例冲激响应求解举例
求系统 dt 2 解：将f(t)→δ(t)， → ，
d2 y(t) +4 d y(t) d f (t) + 3y(t) = + 2 f (t) dt dt
的冲激响应。的冲激响应。
y(t)→h(t) →
d2 h(t ) d h(t ) dδ (t ) +4 + 3h(t ) = + 2δ (t ) 2 dt dt dt
d2 h(t ) d h(t ) dδ (t ) +4 + 3h(t ) = + 2δ (t ) dt 2 dt dt
d2 h( t ) = aδ ′ ( t ) + bδ ( t ) + r ( t ) 1 2 dt d h( t ) 设 = aδ ( t ) + r2 ( t ) dt dt h(