《解三角形》研究性学习评价量规表

格式：doc
大小：35.00 KB
文档页数：2

下载文档原格式

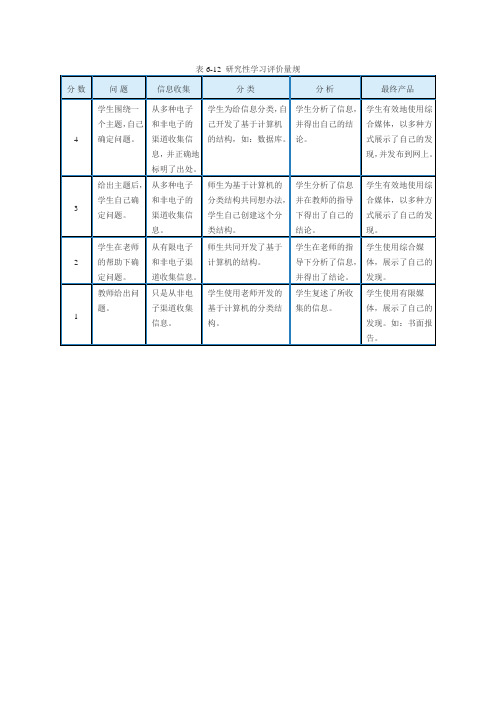
研究性学习评价量规

学生在老师的指导下分析了信息，并得出了结论。
学生使用综合媒体，展示了自己的发现。
1
教师给出问题。
只是从非电子渠道收集信息。
学生使用老师开发的基于计算机的分类结构。
学生复述了所收集的信息。
学生使用有限媒体，展示了自己的发现。如：书面报告。
3
给出主题后，学生自己确定问题。
从多种电子和非电子的渠道收集信息。
师生为基于计算机的分类结构共同想办法，学生自己创建这个分类结构。
学生分析了信息并在教师的指导下得出了自己的结论。
学生有效地使用综合媒体，以多种方式展示了自己的发现。
2学生在Biblioteka 师的帮助下确定问题。从有限电子和非电子渠道收集信息。
师生共同开发了基于计算机的结构。
表6-12研究性学习评价量规
分数
问题
信息收集
分类
分析
最终产品
4
学生围绕一个主题，自己确定问题。
从多种电子和非电子的渠道收集信息，并正确地标明了出处。
学生为给信息分类，自己开发了基于计算机的结构，如：数据库。
学生分析了信息，并得出自己的结论。
学生有效地使用综合媒体，以多种方式展示了自己的发现，并发布到网上。

研究性学习设计方案评价量规表

研究性学习设计方案评价量规表
评价指标
A(5分)
能独立制定详细可行性的活动计划，小组成员都熟悉活动的具体内容和要求语言概括能力强，能用流利标准的普通话表达自己看法；能解答他人问题并能提出质疑；能论述自己的探究过程和结果。有很强的语言驾驭能力。文章观点鲜明，中心突出，材料具体生动，有真情实感。结构严谨，详略得当，语言得体、流畅。善于观察与思考，有较强的搜集和整理资料的能力，并有丰硕成果。积极发表自己的看法，语言有说服力；能注意倾听别人的发言，同时能归纳出发言的重点；能针对别人的发言，提出自己的见解，并且能有理有据。小组成员自觉性高，能主动完成自己的任务，能主动帮助弱势成员完成任务。
5
资源运用资料收集质量成果展示
收集了丰富的资收集了一些资料，收集了一些资料，料，并且都与学习大部分与学习主题只有一小部分与主主题相关相关题相关成果展示形式具有多样性、创新性，数量多，研究的问题得到有效解决，实现了学习目标成果展示形式、数成果展示形式、数量较多，基本能解量较少，不能完全决研究问题，基本实现学习目标实现了学习目标基本上没有收集资料或者资料与主题不相关成果展示很少，不能解决问题或不能实现学习目标
得分
自评
制定计划口头语言表达能力
能通过讨论独立制能独立制定可行性定可行性活动计活动计划，小组成划，小组部分成员员较熟悉活动内容基本熟悉活动内容与要求和要求语言表达能力较强，能用普通话较完整表达自己看法；能较详细介绍现象；能对他人的研究提出质疑有一定的语言功底。文章观点鲜明，中心突出，材料具体，结构完整，条理清楚。语言规范、通顺。肯实践，有一定观察思考能力，能掌握搜集和整理资料的方法，有成果。能发表自己的看法；能注意倾听别人的发言，但归纳不出重点；能针对别人的发言，提出自己的见解。语言表达能力一般，语音、语调较正确，能把自己搜索的资料基本表达出来；较少发表自己的观点文章观点鲜明，材料能表现中心。结构基本完整，有条理。语言基本通顺，有少数错别字。搜集、整理资料的任务需要在他人的帮助下完成，成果不明显。能发表自己的看法；倾听别人的发言不认真，归纳不出重点；能针对别人的发言，提出自己的见解。

研究性学习成果评价量规模板

研究过程
个人活动
1
积极参加小组活动，独立完成积极参加小组活动；工作质量了自己的任务。在活动中积极高，在规定时间内完成个人任帮助有需要的同学。积极追求务，有帮助过其他同学。新知识。采访的家长有代表性（3个或以上不同行业），家长的数量为5个或以上。专家和教师的采访人次为4个或以上。采访过程中有礼貌，有采访提纲书面且问题清楚。采访的家长在3~5个之间，2种不同行业。采访的专家和教师 3个。采访过程中有礼貌，有采访书面提纲但个别问题不够清楚。
采访活动
1.5
参与讨论
1
小专题完成后在论坛发表一篇认真倾听小组伙伴的意见，对不少于150字的主帖，帖中观同伴的反驳有理有据。思维活点清晰，内容较充实，表达无跃，大胆提出有价值的见解。基本错误。在论坛至少回2个帖。海报紧密围绕“寻找错别字” 这个主题，主题鲜明。海报素材获取及加工属原创，无错别字。海报能围绕“寻找错别字”这个主题，主题鲜明。海报素材有部分是直接引用。无错别字。
学习成果成果汇报合计
海报内容
1.5
海报版面
1
海报栏目安排合理，表现形式海报栏目安排比较合理，但表丰富多样，文字排版疏密有现形式不够丰富。图文并茂。间，图文并茂。视觉效果好。视觉效烈的感染力。口头汇报条理清楚，非常自信。能清晰流畅地回答教师或同学提出的与主题相关问题。
80 得分
60
40
20
0 1 2 3 4 5 二级指标 6 7
究性学习成果评价量表
得分需努力(4 自评互评教师评合计分)
9 8 8 16.6
价等级及比率一般(5~6分)
只是用互联网找了老师提供的搜索渠道单一，没网站，收集的有关错别字的信有收集到与错别字息不多，只有一部分和主题有主题不相关。关，且材料零星没有整理能参加小组活动，知道自己的任务,工作可能有一些失误，但能与组员协商解决在规定时间内完成个人的任务。采访的家长少于3个，代表性不强（只有一个行业）。采访的专家和教师为2人次。有书面提纲，但问题不够清楚。知道自己的任务，但在规定时间内未能完成个人的任务，影响小组研究性学习的进度与质量。未对家长进行采访，采访的教师为1 人次。无书面提纲，所提问题不够清楚。

同伴教学评价表-解直角三角形

同伴教学评价表
教师姓名:
日期:11.25
听课人姓名:
学生人数:55
评价要求：关
一、本节课我最喜欢的地方：
老师的《解直角三角形》解直角三角形的应用是在学生掌握了直角三角形的边角关系、三边关系、角角关系后，对锐角三角函数的应用，教师根据学情，将解直角三角形及其应用结合在一起学习，通过创设富有情趣、学生熟知的教学活动情境（比萨斜塔），使学生在熟悉的事物、情境中学习，理解数学，感受数学与现实生活的联系，激发学生学习的热情；在整个课堂中，教师教态亲切和蔼，尊重关怀学生，课堂气氛和谐、民主，体现了和谐的师生关系；在教学过程中，教师注重以生为本，在对例1进行示范讲解后，请学生自主完成例2，并请一名学生进行板书，而后教师通过点评板书及展示学生学案使学生进一步掌握解直角三角形的方法，同时注意引导学生在解题之前先画图，以助解题；教师在教学过程中非常注意细节，对书写要求严谨，
二、本节课如果我上，我会做以下改进：
1、将解直角三角形及其应用放在一起，容量较大； 2、由于内容较多，导致课堂节奏较快，比如例1的解题过程只是通过PPT展示，作为学生解题的模仿对象，如果能够将例1 的解题过程板书在黑板上会更好一些； 3、关于解直角三角形用到的知识背景可以让学生写在学案上，以便做题时参考一下。

高中数学研究性学习评价量规表-

具备的基础知识与技能不理函数,不知道函数求最值的方法和过程.参与过程中的表现不积极参与资料收集,不能提出问题解答其它同学问题,讨论时不和其它同学讨论,只听老师或看书上的.情感与态度表现及发展对学习的内容不感兴趣,学习被动,态度不认真,不能完成老师小组布置的任务.知识技能与应用通过研究性学习,还不能解决生活中简单的优化问题.创新思维提问很少或没有提问，所提的建议和问题方法不够合理。

小计<60理解函数的定义,熟悉函数求最值的方法和过程, 但不会依据具体实际问题选择合适的方法,不会函数建模.理解函数的定义,熟悉函数求最值的方法和过程, 会依据具体实际问题选择合适的方法,会根据实际问题的信息进行函数建模.有解题思路和分析过程.按要求收集资料,按要求和其它同学讨论.并服从安排.提出了自己不懂的问题.并请求帮助,最后解决了自己的问题.积极收集资料,提出自己发现或感兴趣的问题,通过讨论请咨询解决了自己的问题,能够给其它同学提出的问题给予解答与帮助一般,能按要求完成作业.积极配合老师组长的工作.对数学有些兴趣,但对复杂数学问题不感兴趣,态度认真.对学习内容感兴趣,能主动发现并解决问题,在学习与生活中应用数学知识,养成了动脑动手的习惯.通过研究性学习,能解决生活中简单的优化问题，可以用二次函数,线必规划知识解决实际问题.如速度最快、距离最小、费用最低、用料最省等简单问题.能解决常碰到的问题，比如速度最快、距离最小、费用最低、用料最省、效率最高、增长率、膨胀率等。

熟悉应用线性规划，二次函数，数形结合,导数解决问题.数学中的优化问题成果评价量评价等级及分值提问不多，个别建议和问题合理。

敢于提问，所提的个别建议创新、合理。

体现了数学的应用,发展7590价量规理解函数的定义,熟练应用函数求最值,会依据具体实际问题选择合适的方法,会根据实际问题的信息进行函数建模.能得到正确结果并能举一反三,对同一问题能多角度思考,选择多种方法解决.积极收集资料,积极讨论,主动提出有意义的问题与其它同学讨论,并反馈讨论结果,总结得失,能够就其它同学的问题作出解答与分析,帮助其它同学解决他们的问题,能够对老师或其它同学的过程提出自己的看法.最后通过讨论与问题的解答提出解决问题的思路,过程与方法.非常感兴趣,能主动发现问题,并通过各种方式解决问题,把解决结果与其它同学分享,能在生活中应用数学知识.数学思维去认识和解决问题.形成了求真,严谨的学习态度.能解决如速度最快、距离最小、费用最低、用料最省、效率最高、增长率、膨胀率等问题,能从多种角度,选择多种方法来解决,能解决这类问题的综合问题,能选择数据选择的函数来模拟.并通过对结果精确度的对比,得到最准确的结果.善于提问，所提的建议创新、合理,对数学的学习有帮助,体现数学的应用性,灵活性,科学性,创造性.100。

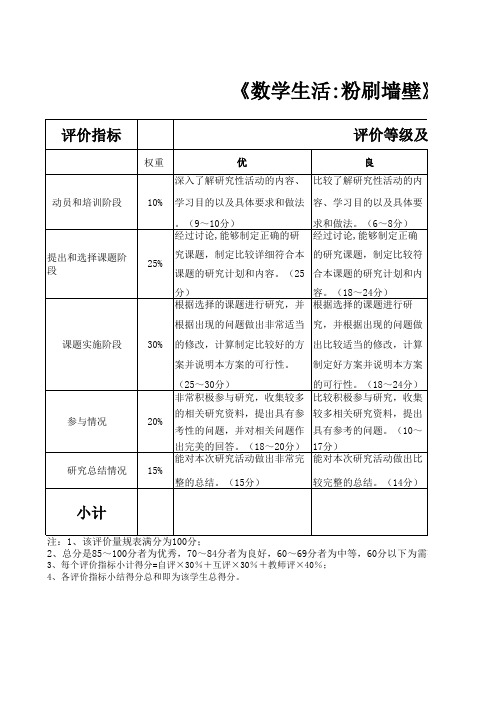
研究性学习成果评价量规

价等级及分值
基本了解研究性活动的内不太了解研究性活动的内容、学习目的以容、学习目的以及具体要及具体要求和做法。求和做法。（5分）（5分以下）经过讨论,能够制定正确经过讨论,不能制定的研究课题，制定基本符正确的研究课题，不会制定本课题的研究合本课题的研究计划和内计划和内容。（10分以下）容。（10～17分）根据选择的课题进行研根据选择的课题进行究，并根据出现的问题做研究，并根据出现的出基本适当的修改，通过问题做出修改，能计计算制定好方案。（8～算制定好方案。（8
17分）分以下）积极参与研究，收集少量参与研究，收集少量的相关研究资料，提出具有参考性的问题。（5～9 相关研究资料。（5
分）分以下）基本能对本次研究活动做不能对本次研究活动出总结。（5～14分）做出总结。（3分） 0 0
分以下为需努力者；
教师评（40％）教师评（40％）
0
25%
究课题，制定比较详细符合本的研究课题，制定比较符课题的研究计划和内容。（25 合本课题的研究计划和内分）容。（18～24分）根据选择的课题进行研究，并根据选择的课题进行研根据出现的问题做出非常适当究，并根据出现的问题做
课题实施阶段
30%
的修改，计算制定比较好的方出比较适当的修改，计算案并说明本方案的可行性。制定好方案并说明本方案
小计
注：1、该评价量规表满分为100分； 2、总分是85～100分者为优秀，70～84分者为良好，60～69分者为中等，60分以下为需努力者
3、每个评价指标小计得分=自评×30％＋互评×30％＋教师评×40％； 4、各评价指标小结得分总和即为该学生总得分。
》研究性学习成果评价量规

研究性学习主题单元评价思维导图和评价量规

研究性学习主题单元评价思维导图和评价量规
根据本教学单元的目标与监督、评估和改进教学的需要，设计以下评价思维导图及评价量规。

一、评价思维导图：
本单元的教学评价从大的方向分为两大块，一是，学生学习的评价；二是教师教学的评价。

学习评价注重的学生学习的整个过程，从课前的准备到学习的过程再到作业的完成情况等；横向来说，也体现了学生知识的学习、资源的应用、作业的设计制作和展示交流，小组的合作等方面。

评价教师的教也主要是围绕教学的准备到课堂的调控和即时的教学效果等等要素来进行。

二、评价量规
主题单元学习评价量规表
综合评语：。

解三角形研究性学习报告

《解三角形的进一步讨论》—-研究性学习报告研究班级：高二(12)班小组组长:张学栋小组成员：唐亮钱智年徐金玉史子军刘晶琳陈敬荣张金年赵峒山李超丁晓瑞秦海龙指导老师：潘金实施时间：2014年10月15日至2015年1月4日一、背景说明：在我国古代就有嫦娥奔月的神话故事。

明月高悬,我们仰望星空,会有无限遐想。

不禁会问，遥不可及的月球离地球到底有多远?1671年,两个法国天文学家测出大约距离为385400千米。

他们是怎样测出的呢？在数学发展史上，受到天文测量、航海测量和地理测量等方面实践活动的推动。

解三角形的理论不断发展,并被用于解决许多测量问题方面。

二、课题目的和意义：三角形是基本的几何图形，三角形中的数量关系是基本的数量关系，有着极其广泛的应用。

我们将在以前学习的有关三角形、三角函数和解直角三角形的知识基础上，通过对于任意三角形边角关系的研究，发现并掌握三角形中的变长与角度之间的数量关系,并解决一些实际问题。

学而不思则罔，只有通过自己的独立思考才能真正学会数学，同时应当掌握科学的思维方法，特别是学习类比、推广等数学思考方法，提高我们的数学思维能力。

三、研究内容：在生产、生活、科技和技术中,我们都会看到许多数学的应用，我们小组主要研究高中数学中以解三角形为中心的一系列问题。

其中包括正弦定理、余弦定理、以及解三角形在实际生活中的一些应用,有天文测量、航海测量和地理测量。

还有解三角形中的一些特殊问题—-海伦公式和秦九韶独出的“三斜求积"公式。

四、研究方法：主要采用数学归纳法、合情推理、建立数学模型、数形结合法、类比、化归、推广等数学思考中常用的逻辑方法。

五、活动步骤及计划安排：（包括成员分工）1、确定研究课题——解三角形的进一步讨论2、成员分工:组长：张学栋，负责与指导教师联系，获取课题信息和研究方法指导，积极协同课题组成员共同研究。

成员：钱智年、徐金玉、唐亮负责收集课题材料。

史子军、刘晶琳、陈敬荣负责对所收集的材料进行分类、整理。

初中数学《三角形》单元评价思维导图以及评价量规

3.解决问题时，除完成各自分工后，同学间还能相互帮助，最后达成解决问题方案。
1.小组有计划，有分工，但不明确。
2.小组汇报的探讨结果是主要是由一两位同学完成的。汇报内容较具体，研究方法科学，有一定的学习价值。
3.小组内有个别同学没有积极参与探讨。
1.小组无计划，无分工。
2.小组汇报的探讨结果是主要是由一两位同学完成的。汇报内容不具体，学习价值一般。
能够得出尺规作图的条件但时间较长且不够完整或得出完整结论但不能准确表没有得出尺规作图的条件需别人帮助动手操作能力能够通过观察分析操作交流研讨等活动完成种以上尺规作图并剪裁
三角形主题单元学习评价
作者姓名
学科
数学
年级
鲁教版六年级
主题单元名称
三角形
单元评价方案的思维导图（说明：将单元评价方案的思维导图导出为jpeg文件粘贴在下面框内；如果提交到平台，则需要使用图片导入的功能，具体操作见《2013学员教师远程研修手册》。）
评价量规（说明：将设计的针对主题单元中某一评价要素的评价量规粘贴在下面）
三角形主题单元“剪裁-尺规作图”评价量规
评价指标
（权重）
评价标准描述
评价
好[1，0.8]
一般（0.8，0.6]
需要改进(0.6,0]
生评
师评
总分和评语
合作能力
（30分）
1.小组有详细计划，和研究目标，分工明确。
2.小组汇报的探究结果是按照分工计划集体合作完成的。汇报内容具体，研究方法科学，有学习价值，有吸引力。
能够完成2种尺规的作图并剪裁
只能完成1种尺规作图。
总分及评语
3.小组内有同学根本没有参与探讨。
思维能力
（35分）

解方程研究性学习评价量规表

了解其他小组研究课题，小组间有时会交流小组之间有时交流解方程知小组之间几乎没有交流解解方程知识资源，互相识资源，很少互相帮助。方程知识资源。帮助。各成员共同进行学习、研究，能较好地开展合作学习，能完成基本的协作，能够较好地完成任务。各成员很少进行共同学习、研究，在合作学习中不够积极主动参与其中，但能在老师引导下帮助同组同学完成任务。各成员之间没有进行共同学习、研究，没有体现小组分工和协作的合作精神，只知道完成自己的工作，各做各的。
解方程应用题的数量关解方程应用题的数量关系系表达比较清晰；且有解方程应用题的数量关系表表达不够清晰；几乎没有运用知识解决实际问题达不够清晰；有运用知识解运用知识解决实际问题的的能力，有继续研究计决实际问题的能力的实例。能力。划。有一定数量分析问题、解决问题能力的例子；有收集生活信息的方法说明；收集信息的能力有了一定的提高。探究性学习体会到数学在生活中的价值；每个成员学习数学的兴趣有了提高；团结合作精神较强。有一定数量分析问题、解决问题能力的例子；有收集生活信息的方法说明；获取、收集、应用信息的能力未能提高。有一定数量分析问题、解决问题能力的例子；有收集生活信息的方法说明；获取、收集、应用信息的能力有提高。
设计方案
研究环节 *0.5
活动情况
*1
小组合作能力
团结协作 *1
活动态度
*1
研究过程
内容记录
0.5
不需要提醒，就能熟练的、准确的，提前完成任务。实践中能灵活应变，及时提出问题，并能分析、归纳和总结问题，解决问题的思路新颖，方法独特，勇于克服困难，积极动脑、动手、动口。活动形式科学合理、能逐步展开。解方程应用题的数量关系表达清晰；有运用知识解决实际问题的能力；有继续研究计划。有一定数量分析问题、解决问题能力的例子；有收集生活信息的方法说明；获取、收集、应用信息的能力有了明显提高。探究性学习体会到数学在生活中的价值；每个成员学习数学的兴趣都有不同层次的提高；团结合作精神强。课题研究过程中遇到问题、困难不退缩。

1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

有交流意识，对自己在正弦定理和余弦定理的探究过程和结果能大致进行解释和评价，能对他人的探究结果质疑。
在交流与评价过程中较少发表自己在研究正弦定理和余弦定理，一般都是跟随某人观点，别人说什么他就跟着说什么，能简单回答他人的一些问题，但不能进行解释。
一般是交流与评价的跟随者，不能对正弦定理和余弦定理的研究进行解说自己的探究过程与结果，也不能对自己和他人的探究过程和结果进行交流和评价。
能与小组成员合作共同去推导正弦定理和余弦定理，能配合一些活动，偶有离群表现
不主动与小组合作去推导正弦定理和余弦定理，不积极去完成，认为任务是他人布置的，必须要别人的监督和指导。
创
新
实
践
善于将自己的设想通过实践解决，能主动通过动手操作去寻求解决方法，有一定的动手能力，具有一定的成果表现。
对正弦定理和余弦定理知识点研究肯动手去实践，有一定的动手能力。
对他人提出出的探究问题理解需要帮助，不能完成探究方案的设计，只能执行他人的设计的方案
合
作
精
神
能与小组成员愉快合作，并能根据三角形、勾股定理等的周长和面积公式知识去推导出正弦定理和余弦定理，从而表现出较强的组织协调能力，一般是小组的领导者。
能与小组成员主动合作去探究圆的周长和面积公式，并能积极配合小组活动，是小组的核心成员。
《解三角形》研究性学习评价量规表
评价指标
评价等级及分值
得分
A（10分）
B（8分）
C（6分）
D（4分）
自评
互评师评参与程度积极参与探究《解三角形》的整个过程，按时完成自己的任务并关心小组探究的进展，积极出谋划策主动取得教师的支持。
主动参与探究《解三角形》，关心小组工作的进展，能完成自己的任务。
主动参与探究《解三角形》，只关心自己的任务，偶有懈怠的表现。
在《解三角形》探究的活动中比较被动，不关心活动的进展，对自己的任务不尽心。
探
究
技
能
能提出探究的问题，能针对探究的目的和条件对《解三角形》进行设计方案与进行研究；能通过网络、书刊、等教学资源进行探究，并能通过实物摆设来构建模型。并与他人共同交流与探讨。
能提出问题，并选定探究的内容，能设计探究方案。
能理解他人提出的探究问题，能设计探究的大致方案。
对正弦定理和余弦定理等方面的知识点的研究不能主动去动手实践，动手实践的工作需要他人的布置和指导。
对于正弦定理和余弦定理等方面的知识点的研究缺少动手能力，拒绝动手实践。
交
流
与
评
价
具有很强的交流意识，能正确评价自己和他人，能论述自己在正弦定理和余弦定理探究过程和结果，对他人的探究过程能提出较深刻的问题并展开民主讨论。