下载文档原格式
第五章 真空中的静电场一、思考讨论题1、电场强度与电势有什么关系？试回答下列问题，并举例说明： （1）场强为零的地方，电势是否一定为零？ （2）电势高的地方，场强是否一定大？ （3）电势相等处，场强是否一定相等？（4）已知某一点的电势，可否求出该点的场强？反之如何？ 解：（1）不一定。
比如两同种点电荷连线中点，场强为零，电势不为零。
（2）不一定。
匀强电场，场强处处相等，而电势不等。
（3）不一定。
点电荷产生的电场线中，电势相等的地方场强方向不一样。
（4）都不可以求。
2、已知某一高斯面所包围的空间内0=∑q ，能否说明穿过高斯面上每一部分的电通量都是0？能否说明高斯面上的场强处处为0？解：由高斯定理∑⎰=⋅=q S d E S1εψ ，0=∑q 仅指通过高斯面的电通量为零，并非场强一定在高斯面处处为零（高斯面外的电荷也在高斯面上各点产生场强）。
3、已知某高斯面上处处E =0，可否肯定高斯面内0=∑q ，可否肯定高斯面处处无电荷？解：可以肯定。
高斯面上处处E =0，0=⋅⎰S d E S，由高斯定理必有0=∑q 。
4、如图1.1所示，真空中有A 、B 两均匀带电平板相互平行并靠近放置，间距为d （d 很小），面积均为S ，带电分别为+Q 和－Q 。
关于两板间的相互作用力，有人说，根据库仑定律应有：2024dQ f πε=； 又有人说，根据f QE =，应有：SQ f 02ε=。
他们说得对吗？你认为f 应等于多少？解：（1）2024dQ f πε=是错误的，因为库仑定律只适用于点电荷，两个带电平板不能直接用库仑定律计算。
（2）SQ f 02ε=也错误。
因为用sqE 0ε=计算的场强是两带电平板产生的合场强，而Eq F =中的场强是一个带电板的电荷量乘以另一个所产生的场强，而不是合场强。
电荷与图1.1自身产生的场强作用力恒为零。
正确答案是：Sq q S qEdq F 02022εε=⋅==⎰ 5、在无限大带电平面和无限长带电直线的电场中，确定各点电荷时，可否选无穷远处为0势点？为什么？解：不能。
习题一一、选择题1．如图所示，半径为R 的圆环开有一小空隙而形成一圆弧，弧长为L ，电荷Q -均匀分布其上。
空隙长为()L L R ∆∆<<，则圆弧中心O 点的电场强度和电势分别为 [ ] （Ａ）200,44Q L Qi R L R πεπε-∆-； （Ｂ）2200,84Q L Qi R L R πεπε-∆-； （Ｃ）200,44Q L Qi R L Rπεπε∆； （Ｄ）200,44Q L Q Li R L RLπεπε-∆-∆。
答案：A解：闭合圆环中心场强为0，则圆弧产生的场强与空隙在圆心处产生的场强之和为0。
由于空隙 ∆l 非常小，可视为点电荷，设它与圆弧电荷密度相同，则所带电荷为/Q L L -∆，产生的场强为204Q L i R L πε∆，所以圆弧产生的场强为204OQ LE i R Lπε-∆=；又根据电势叠加原理可得04O Q U Rπε-= .2．有两个电荷都是＋q 的点电荷，相距为2a 。
今以左边的点电荷所在处为球心，以a 为半径作一球形高斯面。
在球面上取两块相等的小面积S 1和S 2，其位置如图所示。
设通过S 1和S 2的电场强度通量分别为1Φ和2Φ，通过整个球面的电场强度通量为S Φ，则［ ］ （A ）120, /S q εΦ>ΦΦ=； （B ）120, 2/S q εΦ<ΦΦ=；（C ）120, /S q εΦ=ΦΦ=； （D ）120, /S q εΦ<ΦΦ=。
答案：D解：由高斯定理知0Φ=S q ε。
由于面积S 1和S 2相等且很小，场强可视为均匀。
根据场强叠加原理，120,0E E =<，所以12Φ0,Φ0=>。
3．半径为R 的均匀带电球体的静电场中各点的电场强度的大小E 与距球心的距离r 的关系曲线为 [ ]答案：B2∝2∝rRrR解：由高斯定理知均匀带电球体的场强分布为()302041 ()4qrr R R E q r R r πεπε⎧<⎪⎪=⎨⎪>⎪⎩，所以选（B ）。
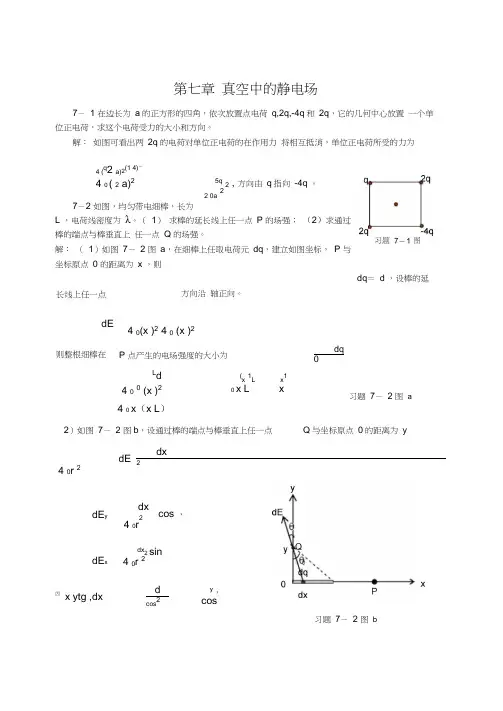
dE ydx24 0rcos ， dE xdx2 sin 4 0r 2因x ytg ,dxdcos2y，cos第七章 真空中的静电场7－ 1 在边长为 a 的正方形的四角，依次放置点电荷 q,2q,-4q 和 2q ，它的几何中心放置 一个单位正电荷，求这个电荷受力的大小和方向。
解： 如图可看出两 2q 的电荷对单位正电荷的在作用力 将相互抵消，单位正电荷所受的力为4 (q 2 a)2(1 4)＝ 4 0 ( 2 a)27－2 如图，均匀带电细棒，长为L ，电荷线密度为 λ。
（ 1） 求棒的延长线上任一点 P 的场强； （2）求通过棒的端点与棒垂直上 任一点 Q 的场强。
解： （ 1）如图 7－ 2 图 a ，在细棒上任取电荷元 dq ，建立如图坐标， P 与坐标原点 0 的距离为 x ，则方向沿 轴正向。
4 0 x （x L ）2）如图 7－ 2 图b ，设通过棒的端点与棒垂直上任一点 dx24 0r 25q2 , 方向由 q 指向 -4q 。
2 0a2dq ＝ d ，设棒的延长线上任一点dE4 0(x )2 4 0 (x )2则整根细棒在P 点产生的电场强度的大小为dq 0Ld4 0 0 (x )2 (x 1Lx 1x L x习题 7－ 2 图 aQ 与坐标原点 0的距离为 ydE 习题 7－ 2 图 b代入上式，则E xdE x sin d x x4 0 y 0 (1 cos 0) ＝ (1 1 )，方向沿 x 轴负向。
4 0 y 4 0 y y 2 L 2EydEy4 0 y 0cos d4 0y sin 0＝ 4 0y y 2 L 27－ 3 一细棒弯成半径为 R 的半圆形，均匀分布有电荷 q ，求半圆中心 O 处的场强。
解： 如图，在半环上任取 dl=Rd 的线元，其上所带的电荷为 dq= Rd 。
对称分析 E y =0。
7－ 4 如图线电荷密度为 λ1的无限长均匀带电直线与另一长度为l 、线电荷密度为 λ2的均匀带电直线在同一平面内，二者互相垂直，求它们间的相互作用力。
第七章 真空中的静电场7－1 在边长为a 的正方形的四角，依次放置点电荷q,2q,-4q 和2q ，它的几何中心放置一个单位正电荷，求这个电荷受力的大小和方向。
解：如图可看出两2q 的电荷对单位正电荷的在作用力 将相互抵消，单位正电荷所受的力为)41()22(420+=a q F πε＝,2520aqπε方向由q 指向-4q 。
7－2 如图，均匀带电细棒，长为L ，电荷线密度为λ。
（1）求棒的延长线上任一点P 的场强；(2)求通过棒的端点与棒垂直上任一点Q 的场强。
解：（1）如图7－2 图a ，在细棒上任取电荷元dq ，建立如图坐标，dq ＝λd ξ，设棒的延长线上任一点P 与坐标原点0的距离为x ，则2020)(4)(4ξπεξλξπεξλ-=-=x d x d dE则整根细棒在P 点产生的电场强度的大小为)11(4)(40020xL x x d E L--=-=⎰πελξξπελ＝)(40L x x L-πελ方向沿ξ轴正向。
（2）如图7－2 图b ，设通过棒的端点与棒垂直上任一点Q 与坐标原点0的距离为y习题7－1图0 dqξd ξ习题7－2 图a204r dxdE πελ=θπελcos 420rdxdE y =， θπελsin 420r dxdE x =因θθθθcos ,cos ,2yr d y dx ytg x ===， 代入上式，则)cos 1(400θπελ--=y ＝)11(4220Ly y+--πελ，方向沿x 轴负向。
θθπελθd ydE E y y ⎰⎰==000cos 4 00sin 4θπελy =＝2204Ly y L+πελ7－3 一细棒弯成半径为R 的半圆形，均匀分布有电荷q ，求半圆中心O 处的场强。
解：如图，在半环上任取d l =Rd θ的线元，其上所带的电荷为dq=λRd θ。
对称分析E y =0。
θπεθλsin 420RRd dE x =⎰⎰==πθπελ00sin 4RdE E x R02πελ= θθπελθd y dE E x x ⎰⎰-=-=0sin 4xdx习题7－2 图byx习题7－3图2022R q επ=，如图，方向沿x 轴正向。
大学物理A习题选解Last revision on 21 December 2020第六章 真空中的静电场习题选解6-1 三个电量为q -的点电荷各放在边长为r 的等边三角形的三个顶点上，电荷(0)Q Q >放在三角形的重心上。
为使每个负电荷受力为零，Q 之值应为多大解：以三角形上顶点所置的电荷(q -)为例，其余两个负电荷对其作用力的合力为1f ，方向如图所示，其大小为题6-1图中心处Q 对上顶点电荷的作用力为2f ，方向与1f 相反，如图所示，其大小为由12f f =，得3Q q =。
6-2 在某一时刻，从238U 的放射性衰变中跑出来的α粒子的中心离残核234Th 的中心为159.010r m -=⨯。
试问：（1）作用在α粒子上的力为多大（2）α粒子的加速度为多大解：（1）由反应238234492902U Th+He →，可知α粒子带两个单位正电荷，即 Th 离子带90个单位正电荷，即 它们距离为159.010r m -=⨯由库仑定律可得它们之间的相互作用力为：（2）α粒子的质量为： 由牛顿第二定律得：6-3 如图所示，有四个电量均为C q 610-=的点电荷，分别放置在如图所示的1，2，3，4点上，点1与点4距离等于点1与点2的距离，长m 1，第3个电荷位于2、4两电荷连线中点。
求作用在第3个点电荷上的力。
解：由图可知，第3个电荷与其它各电荷等距，均为2r m =。
各电荷之间均为斥力，且第2、4两电荷对第三电荷的作用力大小相等，方向相反，两力平衡。
由库仑定律，作用于电荷3的力为题6-3 图 题6-3 图力的方向沿第1电荷指向第3电荷，与x 轴成45角。
6-4 在直角三角形ABC 的A 点放置点电荷C q 91108.1-⨯=，B 点放置点电荷C q 92108.4-⨯-=，已知0.04,0.03BC m AC m ==，试求直角顶点C 处的场强E 。
解：A 点电荷在C 点产生的场强为1E ，方向向下B 点电荷在C 点产生的场强为2E ，方向向右题6-4图根据场强叠加原理，C 点场强 设E 与CB 夹角为θ，21tan E E =θ6-5 如图所示的电荷分布为电四极子，它由两个相同的电偶极子组成。
（真空中的静电场(习题课后作业)(22)1、真空中半径为R 的球体均匀带电，总电量为q ，则球面上一点的电势U=R q 04/πε；球心处的电势U 0=R q 08/3πε 。
(将均匀带电球体微分成球面,利用电势叠加求得结果)2、无限大的均匀带电平面，电荷面密度为σ，P 点与平面的垂直距离为d ，若取平面的电势为零，则P 点的电势Up==-Ed 02/εσd -，若在P 点由静止释放一个电子(其质量为m,电量绝对值为e)则电子到达平面的速率V=0/εσm ed 。
(221mv Ue p=)3.如图，在真空中A 点与B 点间距离为2R,OCD 是以B 点为中心，以R 为半径的半圆路径。
AB两处各放有一点电荷，带电量分别为:+q (A 点)和－q (B 点)，则把另一带电量为Q(Q ＜0)的点电荷从D 点沿路径DCO 移到O 点的过程中，电场力所做的功为=-=)(o D U U Q A R Qq 06/πε-。
4、点电荷Q 被闭合曲面S 所包围，从无穷远处引入另一点电荷q 至曲面外一点，如图所示。
则引入q 前后：( B )(A)曲面S 的电通量不变，曲面上各点场强不变；(B)曲面S 的电通量不变，曲面上各点场强变化；(C)曲面S 的电通量变化，曲面上各点场强不变；(D)曲面S 的电通量变化，曲面上各点场强变化。
5、选择正确答案：( B )(A)高斯定理只在电荷对称分布时才成立。
(B)高斯定理是普遍适用的，但用来计算场强时，要求电荷分布有一定的对称性。
(C)用高斯定理计算高斯面上各点场强时，该场强是高斯面内电荷激发的。
(D)高斯面内电荷为零，则高斯面上的场强必为零。
6、一无限大平面，开有一个半径为R 的圆洞，设平面均匀带电，电荷面密度为σ，求这洞的轴线上离洞心为r 处的场强。
解：利用圆环在其轴线上任一点场强结果2/3220)(4/x R Qx E +=πε任取一细环ρ~ρ+d ρ，ρπρσd dq 2= 2/3220)(4ρπε+=r rdqdE⎰=∞R dE E 222Rr r+=εσ217、真空中一长为L 的均匀带电细直杆，总电量为q ，(1)试求在直杆延长线上距杆的一端距离为a 的p 点的电场强度和电势。
《大学物理A Ⅰ》真空中的静电场习题、答案及解法一、选择题1、一“无限大”均匀带电平面A 的附近放一与它平行的“无限大”均匀带电平面B ，如图1所示。
已知A 上的电荷面密度为σ，B 上的电荷面密度为2σ，如果设向右为正方向，则两平面之间和平面B 外的电场强度分别为 （A ）002εσεσ， （B ）00εσεσ，（C ）00232εσεσ，-（D ）002εσεσ，-[ C ]参考答案： ()0002222εσεσεσ-=-=AB E ()00023222εσεσεσ=+=B E2、在边长为b 的正方形中心处放置一电荷为Q 的点电荷，则正方形顶角处的电场强度大小为 （A ）204bQ πε （B ）202bQ πε （C ）203bQ πε （D ）20bQπε [ C ]参考答案：()202220312241b Q b b QE πεπε=⎥⎥⎦⎤⎢⎢⎣⎡+=3、下面为真空中静电场的场强公式，正确的是［ D ］ （Ａ）点电荷q 的电场0204r r q Ε πε=（r 为点电荷到场点的距离，0r为电荷到场点的单位矢量）（Ｂ）“无限长”均匀带电直线（电荷线密度为λ）的电场302rΕπελ=（r为带电直线到场点的垂直于直线的矢量）（Ｃ）一“无限大”均匀带电平面（电荷面密度σ）的电场0εσ=Ε （Ｄ）半径为Ｒ的均匀带电球面（电荷面密度σ）外的电场0202r r R Ε εσ=（0r为球心到场点的单位矢量）解：由电场强度的定义计算知：A 错，应为0204r r q Επε=，B 不对应为002r rEπελ=,C 应为σ σ2A B图12εσ=E D 对，完整表达应为⎪⎩⎪⎨⎧〉≤=R r r r R Rr E 02020εσ 0202022002044141r rR r r R r r q E εσσππεπε===4、如图2所示，曲线表示球对称或轴对称静电场的场强大小随径向距离r 变化的关系，请指出该曲线可描述下列哪种关系（E 为电场强度的大小）（A ）半径为R 的无限长均匀带电圆柱体电场的r E ~关系 （B ）半径为R 的无限长均匀带电圆柱面电场的r E ~关系 （C ）半径为R 的均匀带电球面电场的r E ~关系 （D ）半径为R 的均匀带正电球体电场的r E ~关系 [ C ] 参考答案：柱形带电体 ⎪⎪⎩⎪⎪⎨⎧≥〈〈=R r r rR Rr r r E 02000202ερερ柱形带电面 ⎪⎩⎪⎨⎧≥〈=R r r r R R r E 000εσ球形带电面 ⎪⎩⎪⎨⎧≥〈=Rr r r Q R r E 020410πε球形带电体 ⎪⎪⎩⎪⎪⎨⎧≥〈〈=Rr r r Q Rr r R r Q E 02003041041πεπε5、如图3所示，曲线表示球对称或轴对称静电场的某一物理量随径向距离r 变化的关系，请指出该曲线可描述下列哪方面内容（E 为电场强度的大小，U 为电势）。
（A ）半径为R 的无限长均匀带电圆柱体电场的E~r 关系 （B ）半径为R 的无限长均匀带电圆柱面电场的E~r 关系 （C ）半径为R 的均匀带正电球体电场的E~r 关系（D ）半径为R 的均匀带正电球面电势的U~r 关系 [ C ]参考答案：r R O E 21r ∝E图221r ∝EORrr ∝图3柱形带电体 ⎪⎪⎩⎪⎪⎨⎧≥〈〈=R r r rR Rr r r E 02000202ερερ柱形带电面 ⎪⎩⎪⎨⎧≥〈=R r r rR R r E 000εσ球形带电面 ⎪⎩⎪⎨⎧≥〈=Rr r rQ Rr E 020410 πε球形带电体 ⎪⎪⎩⎪⎪⎨⎧≥〈〈=R r r r Q Rr r R r Q E 02003041041πεπε球形带电面 ⎪⎩⎪⎨⎧≥〈=Rr r r Q R r E 020410 πε球形带电面 ⎪⎪⎩⎪⎪⎨⎧〉≤〈=Rr rQ Rr R QU 0041041πεπε6、一均匀电场E 的方向与x 轴同向，如图4所示，则通过图中半径为R 的半球面的电场强度的通量为（A ）0 （B ）22ΕR π （C ）ΕR 22π （D ）ΕR 2π[ A ]解：因为穿入与穿出半球面的E 通量相等，总和为零，所以答案A 正确。
7、如果一高斯面所包围的体积内电荷代数和C 10850.812∑-⨯=q ，则可肯定： （A ）高斯面上各点场强可均为零（B ）穿过高斯面上每一面元的电场强度通量均为C m 1N 2⋅ （C ）穿过整个高斯面的电场强度通量为C m 1N 2⋅（D ）以上说法都不对 [ C ]参考答案：⎰∑==∙Sn i i q S d E 11ε()121C m N 11-=⋅⋅==∙⎰∑Sni iqS d E εOxE图48、如图5所示，在半径为R 的“无限长”均匀带电圆筒的静电场中，各点的电场强度E 的大小与距轴线的距离r 关系曲线为[ A ]参考答案：柱形带电面 ⎪⎩⎪⎨⎧≥〈=Rr r r R r E 00210λπε9、两个同心均匀带电球面，半径分别为b a R R 和（a R ＜b R ），所带电荷分别为b a Q Q 和。
设某点与球心相距r ，当b R ＜r 时，该点的电场强度的大小为 (A)⎪⎪⎭⎫ ⎝⎛+⋅22041b b a R Q r Q πε (B)2041r Q Q ba +⋅πε (C)241r Q Q b a -⋅πε (D)2041r Q a⋅πε [ B ] 参考答案：⎰∑==∙Sn i i q S d E 11εb a a R r R r rQ E 〈〈=2041πε10、根据真空中的高斯定理，判断下列说法正确的是（A ）闭合面内的电荷代数和为零时，闭合面上各点场强不一定处处为零 （B ）闭合面内的电荷代数和不为零时，闭合面上各点场强一定处处不为零 （C ）闭合面内的电荷代数和为零时，闭合面上各点场强一定为零 （D ）闭合面上各点场强均为零时，闭合面内一定处处无电荷[ A ]参考答案：⎰∑==∙Sni iqS d E 11ε11、根据静电场中电势的定义，静电场中某点电势的数值等于 （A ）单位试验电荷置于该点时具有的电势能 （B ）试验电荷0q 置于该点时具有的电势能（C ）把单位正电荷从该点移到电势零点时外力所做的功r 1∝EORr E(A)ORr Er 1∝E (B)ORr E (C)r 1∝E ORrE(D)r1∝E 图5（D ）单位试验正电荷置于该点时具有的电势能 [ C ]参考答案：由电势的定义只有C 对12、如图6所示，在点电荷q 的电场中，在以q 为中心、R 为半径的球面上，若选取P 处作电势零点，则与点电荷q 距离为r 的P '点的电势为[ A ] （A ）⎪⎭⎫⎝⎛-⋅r R q1140πε （B ）⎪⎭⎫ ⎝⎛-⋅R r q 1140πε（C ）()R r q -04πε （D ）r q 04πε参考答案：⎪⎭⎫ ⎝⎛-=⎪⎭⎫⎝⎛--==⎰'r R R r dr r Q U rRa p 11411141410020πεπεπε13、图7中实线为某电场中的电场线，虚线表示等势（位）面，由图可看出： （A ）C B AC B A U U ，U >>E <E <E （B ）C B AC B A U U ，U <<E <E <E （C ）C B AC B A U U ，U >>E >E >E（D ）C B AC B A U U ，U<<E >E >E [ D ]参考答案：电力线密集处电场强度大，电力线指向电势下降方向。
二、填空题1、根据电场强度的定义，静电场中某点的电场强度为 单位正试验电荷置于该点时所受到的 电场力。
参考答案：单位正试验电荷置于该点时所受到的。
2、电量为C 1049-⨯的试验电荷放在电场中某点时，受到N 1089-⨯的向下的力,则该点的电场强度大小为1C N 2-⋅，方向 向下 。
参考答案：0q FE= ()1990C N 2104108---⋅=⨯⨯==q F E 3、A 、B 为真空中两个平行的“无限大”的均匀带电平面，已知两平面 间的电场强度大小为0E ，两平面外侧电场强度大小都为30E ，方向如 图8所示，则A 、B 两平面上的电荷面密度分别为=A σ0032E ε-， R qP PrP '图6ABC图70E30E 30EA B图8=B σ0034E ε-。
参考答案：⎪⎪⎩⎪⎪⎨⎧+=-=-00000022322εσεσεσεσB A B A E E ⎪⎪⎩⎪⎪⎨⎧-=-=∴34320000E E B A εσεσ 4、在静电场中，任意作一闭合曲面，通过该闭合曲面的电场强度通量⎰⋅S d E的值取决于 闭合曲面内的电荷量 ，而与 电荷量的分布 无关。
参考答案：∑⎰==∙ni i Sq S d E 101ε5、如图9所示，点电荷q 2和q -被包围在高斯面S 内，则通过该高斯面的电场强度通量⎰=⋅SqS d E 0ε，式中E为 高斯面任意点 处的场强。
6、如图10所示，试验电荷q 在点电荷+Q 产生的电场中，沿半径为R 的43圆弧轨道由a 点移到b 点，再从d 点移到无穷远处的过程中，电场力做的功为RqQ04πε-。
参考答案：⎪⎭⎫ ⎝⎛=⎪⎭⎫ ⎝⎛-∞-===⎰∞R qQ R qQ dr r Q q qU W R14114410020πεπεπε7、如图11所示，在静电场中，一电荷C 106.119-⨯=q 沿41圆弧轨道从A点移到B 点，电场力做功J 102.315-⨯，当质子沿43圆弧轨道从B 点回到A 点时，电场力做功=W J 102.315-⨯-，设B 点电势为零，则A 点的电势=V V 1024⨯。
参考答案： ()V 102106.1102.341915⨯=⨯⨯==--q W U A8、一均匀静电场，电场强度()1m V 2050-⋅+=j i E，则点()2,4a 和点()0,2b 之间的电势差V 140-。
（点的坐标x 、y 以m 计）S+2q-q图a d∞＋Qq 图10图11OBA参考答案：()⎰⎰⎰⎰⎰-=+=+=∙=24022402V 1402050dx dx dx E dx E l d E U y x b aab9、如图12所示，在电荷为q 的点电荷的静电场中，将一电荷为0q 的试验电荷从a 点经任意路径移动到b 点，外力克服静电场力所做的功=W ⎪⎪⎭⎫ ⎝⎛-b ar r q q 11400πε。
参考答案：⎪⎪⎭⎫ ⎝⎛-=⎪⎪⎭⎫ ⎝⎛--===⎰'b a a br r p r r qq r r qq dr r qq U q W ba1141144100002000πεπεπε三、计算题1、用绝缘细线弯成的半圆环，半径为R ，其上均匀地带有正电荷Q ，试求圆心的电场强度。
