关于投影变形的讨论

罗宾逊投影变形特征
罗宾逊投影是一种常见的地图投影方式，其变形特征主要包括以下几个方面：1.等面积变形：罗宾逊投影可以保持地图上各区域的面积比例不变，这使得该投影在
表示地区分布和面积对比方面具有优势。

2.低纬度地区变形较大：在低纬度地区，罗宾逊投影的变形较大，这可能导致地图上
的形状和方向出现较大的误差。

随着纬度的升高，变形逐渐减小。

3.保持赤道和经线真实：在赤道和中央经线附近，罗宾逊投影能够保持形状和方向的
准确性，因此对于表示赤道附近地区的地图非常适用。

4.连续性强：罗宾逊投影的连续性强，特别是在高纬度地区，这使得地图上的轮廓线
更加平滑，便于阅读和使用。

总的来说，罗宾逊投影在保持等面积、保持赤道和经线真实以及连续性强等方面具有显著的优势，因此在地图制作中得到了广泛应用。

然而，它也存在一定的局限性，尤其是在低纬度地区，变形较大可能会影响地图的准确性和可靠性。

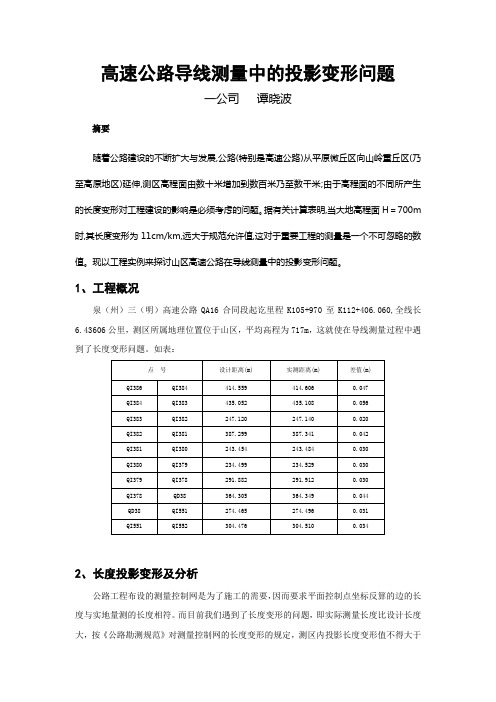
高速公路导线测量中的投影变形问题一公司谭晓波摘要随着公路建设的不断扩大与发展,公路(特别是高速公路)从平原微丘区向山岭重丘区(乃至高原地区)延伸,测区高程面由数十米增加到数百米乃至数千米;由于高程面的不同所产生的长度变形对工程建设的影响是必须考虑的问题。

据有关计算表明,当大地高程面H＝700m 时,其长度变形为11cm/km,远大于规范允许值,这对于重要工程的测量是一个不可忽略的数值。

现以工程实例来探讨山区高速公路在导线测量中的投影变形问题。

1、工程概况泉（州）三（明）高速公路QA16合同段起讫里程K105+970至K112+406.060,全线长6.43606公里，测区所属地理位置位于山区，平均高程为717m，这就使在导线测量过程中遇到了长度变形问题。

如表：2、长度投影变形及分析公路工程布设的测量控制网是为了施工的需要，因而要求平面控制点坐标反算的边的长度与实地量测的长度相符。

而目前我们遇到了长度变形的问题，即实际测量长度比设计长度大，按《公路勘测规范》对测量控制网的长度变形的规定，测区内投影长度变形值不得大于2.5 cm/km ，即投影变形应达到1/40 000的精度。

这就要求要对实测长度进行改正，也就是要先将控制网边长归化到参考椭球面上，然后再将椭球面上的长度投影到高斯平面上，使其影响可以忽略不计。

2.1、投影变形数学模型长度变形来源于以下两个方面:2.1.1 实地测量的边长长度换算到椭球面上产生的变形,即1s ∆;改正数误差方程式(此式较复杂这里省略)经最小二乘列出误差方程式,按级数展开后取其主项(其它项的影响甚微可以忽略不计):s R H s Am-=∆1（1） 式中 A R -长度所在方向的椭球曲率半径；m H -长度所在高程面对于椭球面的平均高程； s -实地测量的水平距离。

2.1.2 椭球面上的长度投影至高斯平面02222s Ry s m+=∆ （2）式中 R -测区中点的平均曲率半径； m y -距离的2端点横坐标平均值； 0s -为归算到椭球面上的长度。

线路工程控制测量投影变形问题分析和探讨摘要：介绍了线路工程控制测量中应考虑的变形因素，以及减少长度变形的几种常用手段，举例分析了某原水管道连通工程控制测量在地方城建坐标系下采用建立“抵偿高程面”的具体方法，并以实际数据验证其有效性。

关键词：控制测量长度变形抵偿变形投影带抵偿高程面1.问题的提出依据我国的工程测量规范规定，建立平面控制网的坐标系统应该保证长度综合变形不超过2.5cm/km.（相对变形不超过1/40000）。

在线路工程控制测量中，长度变形是一个不可以避免的问题，我们可以采取一些技术手段来使长度变形减弱，将长度变形控制在允许的范围之内，使平面控制点坐标反算边的长度与实地量测的长度相符，以满足工程测量规范的要求。

2.长度投影变形分析由参考文献：2可知，投影变形主要由于以下两种因素引起的：2.1参考椭球面归算变形因素：（1）式中，为平均高程面高程（相对于参考投影面），为地面上的实际长度，为高斯投影归算边长，为归算边两端点横坐标平均值。

2.2高斯投影归算变形因素：（2）式中，≈，一般可以将参考椭球视为圆球，取圆球半径≈6371km。

由公式（1）看出，将实地距离由较高的高程面归化算至较低的参考椭球面时，长度总是缩短的；值与成正比，随增大而增大。

由公式（2）看出，将参考椭球面上的距离化算至高斯平面时，长度总是增长的。

值随增大而增大，离中央子午经线越远变形越大。

理论上，当两项改正值大小相等时，长度变形为零。

（3）由上述分析可知，减少投影长度变形问题的主要思路为以下三种：（1）建立“抵偿变形投影带”高斯投影坐标系“抵偿变形投影带” 高斯投影坐标系的建立是在保持国家统一的椭球投影面不变的基础上，选择合适的中央子午线，使长度高斯投影变形恰好抵偿其投影到归化椭球面所产生的变形。

为了确定“抵偿变形投影带”的中央子午线的位置，取高斯投影坐标正算公式，同时由，。

可算出。

式中，B，L为测区中心位置的维度和经度，为标准分带经度与抵偿变形投影带中央子午线经度之差。

一、实验目的本次实验旨在了解地球球面投影到平面时产生的变形，掌握地图投影的变形特征，分析不同投影方式对地图变形的影响，提高对地图投影变形的认识。

二、实验原理地球椭球面是一个不可展的曲面，而地图是一个平面。

在将地球椭球面上的经纬线网描绘成平面图形的过程中，必然会发生各种变形。

这些变形主要包括长度变形、角度变形和面积变形。

地图投影就是研究如何将地球椭球面上的经纬线网准确地描绘到平面上的方法。

三、实验材料与工具1. 地球仪2. 白纸3. 铅笔4. 剪刀5. 比例尺6. 地图投影软件（如Google Earth）四、实验步骤1. 将地球仪放置在桌面上，用铅笔在白纸上画出地球仪的大致轮廓。

2. 使用剪刀将白纸沿地球仪轮廓剪下，得到一个近似球面的平面。

3. 在地球仪上选取一个经纬度点，用铅笔在白纸上标记出该点的位置。

4. 将地球仪上的经纬线网描绘到白纸上，注意保持经纬线之间的相对位置。

5. 使用比例尺测量白纸上的经纬线长度，并与地球仪上的实际长度进行比较，分析长度变形。

6. 在白纸上选择一个点，测量该点所在经线的角度，并与地球仪上的实际角度进行比较，分析角度变形。

7. 使用地图投影软件，将地球仪上的经纬线网投影到平面地图上，比较不同投影方式下的地图变形。

五、实验结果与分析1. 长度变形在实验过程中，我们发现白纸上的经纬线长度与地球仪上的实际长度存在差异。

这是因为地球椭球面是不可展的曲面，而白纸是一个平面。

在将地球椭球面上的经纬线网描绘到白纸上时，必然会发生长度变形。

根据实验结果，我们可以发现，在地球仪的赤道附近，长度变形较小；而在两极附近，长度变形较大。

2. 角度变形实验结果表明，白纸上的经纬线角度与地球仪上的实际角度存在差异。

这是由于地球椭球面是不可展的曲面，而在将地球椭球面上的经纬线网描绘到白纸上时，角度变形不可避免。

根据实验结果，我们可以发现，在地球仪的赤道附近，角度变形较小；而在两极附近，角度变形较大。

由中央子午线引起的投影变形问题的解决方法摘要：本文对由于中央子午线所引起的投影变形问题进行了分析，根据各规范要求，提出了解决方案，并以工程实例进行说明。

关键词：中央子午线投影变形0 引言在接到工程任务后，首先要搜集控制点资料，并对搜集的控制点资料进行分析及验证，在一些工程中存在对控制点或地形图的投影变形问题，尤其是在长距离的跨带工程中必须解决好投影变形问题，否则会导致地形图上的长度与实际长度不符。

1 对工程中由中央子午线引起的投影变形问题的控制，各规范的规定如下1.1 根据《水运工程测量规范》的要求，平面坐标系统的确定应符合：平面控制网的坐标系统应采用统一的高斯正形投影平面直角坐标系，对l：500 地形测图及港口工程施工测量，测区距投影带中央子午线的距离大于45km 时，可采用任意带投影。

一个测区应采用同一坐标系，对港口工程测量和比例尺不小于1：1000 的疏浚及航道测量，其长度投影变形不应大于1/40000；对比例尺小于1：1000 的疏浚及航道测量，其投影变形不应大于1/20000。

1.2 根据《工程测量规范》的要求，测区内投影长度变形值不大于2.5cm/km,因此在测量实践中，常根据工程区域所处的地理位置和平均高程，按以下方法选择坐标系：当边长投影改正量不大于2.5cm/km 时，采用高斯正形投影3°带平面直角坐标系；当边长投影改正量大于2.5cm/km 时，采用投影于抵偿高程面上的高斯正形投影3°带平面直角坐标系或采用投影于1954年北京坐标系或1980 西安坐标系椭球面上的高斯正形投影任意带平面直角坐标系；2 投影变形问题的解决方法投影于抵偿高程面上的高斯正形投影任意带平面直角坐标系；长距离线路工程往往跨度很大，且在勘测设计时需全线贯通，单纯采用上述方法选择坐标系不能有效地控制投影长度变形值，如某高等级公路的测量控制网，东西跨度超过200km，以线路中心的经度为中央子午线，采用投影于1954 年北京坐标系椭球面上的高斯正形投影任意带平面直角坐标系，使线路两端的边长投影改正量大于12cm/km，远远大于投影长度变形值不大于2.5cm/km,即卩1/40000的边长误差要求，导致每条放样边长需改正，给工程施工放样带来诸多不便。

关于工程控制测量中投影长度变形值超限的处理分析工程控制测量是工程建设中非常重要的一环，它可以保证工程施工的精准度和稳定性。

在工程控制测量中，投影长度变形值是一个重要的指标，它可以反映出测量过程中的变形情况，当投影长度变形值超限时，需要及时进行处理分析，以保证工程施工的质量和安全。

本文将分析关于工程控制测量中投影长度变形值超限的处理方法和分析过程。

一、投影长度变形值的概念和作用投影长度变形值是指实际测量与理论测量之间的差值，它可以体现出工程测量中的误差和变形情况。

其主要作用有以下几点：1. 反映测量精度：投影长度变形值可以反映出测量过程中的精度和准确度，帮助工程人员了解测量结果的可信度，从而保证工程施工的精准度。

2. 预警工程变形：投影长度变形值超限可以预警工程变形情况，及时发现和修复工程中的变形问题，从而保证工程的安全和稳定。

3. 提高测量质量：通过及时处理分析投影长度变形值超限的问题，可以不断改进测量技术和流程，提高测量的准确性和精度。

投影长度变形值超限可能由以下几个方面的原因造成：1. 测量设备问题：测量设备的性能不稳定或者损坏会导致测量结果出现偏差，从而造成投影长度变形值超限。

2. 测量环境问题：测量时的环境因素，如气温、湿度、风力等的变化会对测量结果产生影响，导致投影长度变形值超限。

3. 测量操作问题：操作员的技术水平和操作规范与否，会直接影响测量结果的准确性，从而导致投影长度变形值超限。

4. 工程变形问题：工程本身的变形、位移等问题也会导致投影长度变形值超限，需要及时处理分析并进行修复。

三、处理分析投影长度变形值超限的方法当投影长度变形值超限时，需要及时进行处理分析，并采取相应的措施进行修复。

处理分析的方法主要包括以下几个方面：1. 检查测量设备：首先需要检查测量设备的性能和稳定性，确保测量设备的准确度和精度，必要时需要进行维护和保养。

2. 调整测量环境：对于测量环境的因素，需要进行合理的调整，如控制温度湿度，选择合适的天气条件等，以保证测量结果的准确性。

高海拔投影变形的原因
高海拔投影变形是指在高山或高海拔地区进行测量或拍摄时，由于地球曲率、大气折射等因素影响，所得到的图像或测量数据与实际情况存在偏差。

造成高海拔投影变形的原因主要有以下几个方面：
1.地球曲率影响：随着高度的增加，地球曲率的作用越来越大，因此高海拔地区的投影变形也越明显。

2.大气折射影响：大气在不同温度、湿度和气压下的密度不同，会产生不同程度的折射现象，导致高海拔地区的图像出现扭曲、变形等情况。

3.地形起伏影响：高山地区地形起伏较大，地表高差较大，导致光线在传播过程中发生折射、反射等现象，从而影响图像的精度。

4.摄影设备影响：高海拔地区气温低、氧气稀薄、地形复杂，对摄影设备的要求也比较高，若设备不够先进或不适应当地环境，也会导致投影变形。

综上所述，高海拔投影变形是由多种因素综合作用产生的，需要综合考虑各种因素，采取合适的测量或拍摄方法，才能得到更准确的图像或测量数据。

- 1 -。

投影变形什么是投影变形？投影变形是指通过透镜或镜头对影像进行变形处理的一种技术。

它可以改变影像的形状和尺寸，达到特定的效果或目的。

投影变形技术广泛应用于电影、摄影、艺术展示等领域，是现代图像处理的重要技术手段之一。

投影变形的原理投影变形的原理基于光学物理学和几何学。

当光线经过特定形状的镜头或透镜时，它会受到折射或反射的作用，从而改变光线的传播方向和路径。

利用这种原理，可以实现对影像的形状、大小和投影角度的调整。

投影变形的应用领域1. 电影和电视在电影和电视制作中，投影变形是一项重要的特效技术。

通过对影像进行变形处理，可以实现各种特殊效果，如人物变形、世界扭曲等。

例如，在电影《哈利·波特与混血王子》中，利用投影变形技术实现了角色形象的变形效果，增强了影片的视觉冲击力和艺术表现力。

2. 摄影艺术在摄影艺术中，投影变形技术常用于创作独特的影像效果。

摄影师可以利用特殊的镜头或透镜，对被摄物体的形状进行变形处理，从而创造出独特的视觉效果。

这种技术常用于拍摄建筑、风景和人物等主题。

3. 艺术展示在艺术展示中，投影变形技术常用于实现艺术家的创意和表达。

通过将特殊形状的投影映射到艺术品或装置上，可以改变其形状和外观，创造出惊人的视觉效果。

这种技术常用于艺术展览、装置艺术和舞台表演等领域。

投影变形的技术方法1. 几何投影变形几何投影变形是一种基于几何学的投影变形方法。

它通过对三维模型的几何信息进行变换和调整，从而实现对影像的形状和尺寸的变化。

这种方法需要对目标模型进行详细的几何分析和计算，较为复杂。

2. 纹理投影变形纹理投影变形是一种基于影像纹理的投影变形方法。

它将目标影像的纹理信息映射到特定的形状转变上，从而实现影像的形状和尺寸的改变。

相比几何投影变形，纹理投影变形更加简单和直观，常用于实时渲染和交互式应用。

3. 光学投影变形光学投影变形是一种基于光学物理学的投影变形方法。

它利用特殊形状的镜头或透镜对入射光进行折射或反射，从而实现对影像的形状和位置的调整。