第7章习题解答
- 格式:doc
- 大小:202.00 KB
- 文档页数:7

第7章 气体动理论7.1基本要求1.理解平衡态、物态参量、温度等概念,掌握理想气体物态方程的物理意义及应用。
2.了解气体分子热运动的统计规律性,理解理想气体的压强公式和温度公式的统计意义及微观本质,并能熟练应用。
3.理解自由度和内能的概念,掌握能量按自由度均分定理。
掌握理想气体的内能公式并能熟练应用。
4.理解麦克斯韦气体分子速率分布律、速率分布函数及分子速率分布曲线的物理意义,掌握气体分子热运动的平均速率、方均根速率和最概然速率的求法和意义。
5.了解气体分子平均碰撞频率及平均自由程的物理意义和计算公式。
7.2基本概念1 平衡态系统在不受外界的影响下,宏观性质不随时间变化的状态。
2 物态参量描述一定质量的理想气体在平衡态时的宏观性质的物理量,包括压强p 、体积V 和温度T 3 温度宏观上反映物体的冷热程度,微观上反映气体分子无规则热运动的剧烈程度。
4 自由度确定一个物体在空间的位置所需要的独立坐标数目,用字母i 表示。
5 内能理想气体的内能就是气体内所有分子的动能之和,即2iE RT ν= 6 最概然速率速率分布函数取极大值时所对应的速率,用p υ表示,p υ==≈其物理意义为在一定温度下,分布在速率p υ附近的单位速率区间内的分子在总分子数中所占的百分比最大。
7 平均速率各个分子速率的统计平均值,用υ表示,υ==≈8 方均根速率各个分子速率的平方平均值的算术平方根,用rms υ表示,rms υ==≈ 9 平均碰撞频率和平均自由程平均碰撞频率Z 是指单位时间内一个分子和其他分子平均碰撞的次数;平均自由程λ是每两次碰撞之间一个分子自由运动的平均路程,两者的关系式为:Zυλ==或λ=7.3基本规律1 理想气体的物态方程pV RT ν=或'm pV RT M=pV NkT =或p nkT =2 理想气体的压强公式23k p n ε=3 理想气体的温度公式21322k m kT ευ==4 能量按自由度均分定理在温度为T 的平衡态下,气体分子任何一个自由度的平均动能都相等,均为12kT 5 麦克斯韦气体分子速率分布律 (1)速率分布函数()dNf Nd υυ=表示在速率υ附近单位速率区间内的分子数占总分子数的百分比或任一单个分子在速率υ附近单位速率区间内出现的概率,又称为概率密度。


第七章(一阶电路)习题解答一、选择题1.由于线性电路具有叠加性,所以 C 。
A .电路的全响应与激励成正比;B .响应的暂态分量与激励成正比;C .电路的零状态响应与激励成正比;D .初始值与激励成正比2.动态电路在换路后出现过渡过程的原因是 A 。
A . 储能元件中的能量不能跃变;B . 电路的结构或参数发生变化;C . 电路有独立电源存在;D . 电路中有开关元件存在3.图7—1所示电路中的时间常数为 C 。
A .212121)(C C C C R R ++; B .21212C C C C R +;C .)(212C C R +;D .))((2121C C R R ++解:图7—1中1C 和2C 并联的等效电容为21C C +,而将两个电容摘除后,余下一端口电路的戴维南等效电阻为2R ,所以此电路的时间常数为)(212C C R +。
4.图7—2所示电路中,换路后时间常数最大的电路是 A 。
解:图7—2(A )、(B )、(C )、(D )所示四个电路中的等效电感eq L 分别为M L L 221++、21L L +、M L L 221-+和M L L 221++。
0>t 时,将图6—2(A )、(B )、(C )、(D )中的电感摘除后所得一端口电路的戴维南等效电阻eq R 分别为2R 、2R 、2R 和21R R +。
由于RL 电路的时间常数等于eqeq R L ,所以图7—2(A )所示电路的时间常数最大。
5.RC 一阶电路的全响应)e610(10tc u --=V ,若初始状态不变而输入增加一倍,则全响应c u 变为 D 。
A .t10e1220--; B .t10e620--;C .t10e1210--; D.t10e1620--解:由求解一阶电路的三要素法 τtc c c c u u u u -+∞-+∞=e)]()0([)( 可知在原电路中10)(=∞c u V ,4)0(=+c u V 。

习 题7-1为什么一般矩形波导测量线的槽开在波导宽壁的中线上?答:因为矩形波导一般工作于10TE 模,由10TE 模的管壁电流知,在矩形波导宽壁中线处只有纵向电流,因此沿波导宽壁的中线开槽不会切断高频电流的通路,不会破坏波导内的场结构,也不会引起波导内的电磁波向外辐射能量。
7-2 推导矩形波导中mn TE 波的场量表达式。
7-3 已知空气填充的矩形波导截面尺寸为21023mm b a ⨯=⨯,求工作波长mm 20=λ时,波导中能传输哪些模式?mm 30=λ时呢? 解:矩形波导的截止波长22c 2⎪⎭⎫ ⎝⎛+⎪⎭⎫ ⎝⎛=b n a m πππλ当0,1==n m 时,mm a C 462==λ,1,0==n m 时,mm b C 202==λ, 0,2==n m 时,mm a C 23==λ, 1,1==n m 时,mm b a 34.181********222c =⎪⎭⎫⎝⎛+⎪⎭⎫ ⎝⎛=⎪⎭⎫ ⎝⎛+⎪⎭⎫ ⎝⎛=πππλ满足电磁波在波导中传播条件c λλ<的模式有10TE 、01TE ;当mm 30=λ时,只能传输10TE 模。
7-4 已知空气填充的矩形波导截面尺寸为248cm b a ⨯=⨯,当工作频率GHz 5=f 时,求波导中能传输哪些模式?若波导中填充介质,传输模式有无变化?为什么?解: cm f C 6105103910=⨯⨯==λ,矩形波导的截止波长22c 2⎪⎭⎫⎝⎛+⎪⎭⎫ ⎝⎛=b n a m πππλ,当0,1==n m 时,cm a C 162==λ,1,0==n m 时,cm b C 82==λ, 0,2==n m 时,cm a C 8==λ, 2,0==n m 时,cm b C 4==λ 1,1==n m 时,mm b a 15.74181222222c =⎪⎭⎫⎝⎛+⎪⎭⎫ ⎝⎛=⎪⎭⎫ ⎝⎛+⎪⎭⎫ ⎝⎛=πππλ满足电磁波在波导中传播条件c λλ<的模式有10TE 、01TE 、20TE 、11TE 、11TM ; 若波导中填充介质,工作波长变短,所以传输模式增多。
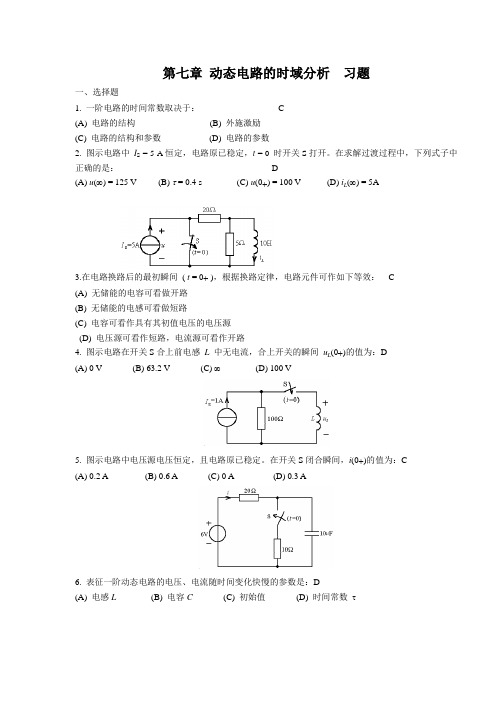
第七章动态电路的时域分析习题一、选择题1. 一阶电路的时间常数取决于: C(A) 电路的结构(B) 外施激励(C) 电路的结构和参数(D) 电路的参数2. 图示电路中I S = 5 A恒定,电路原已稳定,t = 0时开关S打开。
在求解过渡过程中,下列式子中正确的是: D(A) u(∞) = 125 V (B) τ = 0.4 s (C) u(0+) = 100 V (D) i(∞) = 5AL3.在电路换路后的最初瞬间( t = 0+ ),根据换路定律,电路元件可作如下等效: C(A) 无储能的电容可看做开路(B) 无储能的电感可看做短路(C) 电容可看作具有其初值电压的电压源(D) 电压源可看作短路,电流源可看作开路(0+)的值为:D4. 图示电路在开关S合上前电感L中无电流,合上开关的瞬间uL(A) 0 V (B) 63.2 V (C) ∞(D) 100 V5. 图示电路中电压源电压恒定,且电路原已稳定。
在开关S闭合瞬间,i(0+)的值为:C(A) 0.2 A (B) 0.6 A (C) 0 A (D) 0.3 A6. 表征一阶动态电路的电压、电流随时间变化快慢的参数是:D(A) 电感L(B) 电容C(C) 初始值(D) 时间常数τ7. 图示正弦脉冲信号的数学表达式为:B (A) sin ω t ⋅ ε (t ) + sin ω ( t - T ) ⋅ ε ( t - T ) (B) sin ω t ⋅ ε (t ) - sin ω t ⋅ ε ( t - T ) (C) sin ω t ⋅ ε (t ) - sin ω ( t - T ) ⋅ ε ( t - T ) (D) sin ω t ⋅ ε (t ) + sin ω t ⋅ ε ( t - T )8. 图示电路中,原已达稳态, t = 0开关 S 打开,电路的时间常数为:D (A)s 41 (B) s 61(C) s 4 (D)s 69. 示电路中,t = 0 时开关打开,则 u (0+)为:C(A) 0V (B) 3.75V (C) – 6V (D) 6V10.图示电路中,开关打开已久,在 t = 0 时开关闭合,i (0+) 为:D(A) 0A (B) 0.8A(C) 2A (D)1A11.R 、C 串联电路,已知全响应()()10C 83V,0t u t e t -=-≥,其零状态响应为:(A )(A) 1088V te-- (B) 1083V t e -- (C) 103V t e -- (D) 105V t e -12. .一阶电路的全响应()()10C 106V,0tu t et -=-≥若初始状态不变而输入增加一倍,则全响应u C (t)为 ( D ) (A) 20-12e -10t ; (B) 20-6e -10t ; (C) 10-12e -10t ; (D) 20-16 e -10t 。

第七章习题解答2、试确定系数a ,b 的值使220[()cos ]ax b x dx p+-ò达到最小解:设220(,)[()cos ]I a b ax b x dx p=+-ò确定a ,b 使(,)I a b 达到最小,必须满足0,0I Ia b ¶¶==¶¶即3222222000022222000012[cos ]0cos 248212[cos ]0cos 82a b ax b x xdx a x dx b xdx xxdx a b ax b x dx a xdx b dx xdx p p p p p p p pp p p p p ììì+=-+-=+=ïïïïïïÞÞíííïïï+=+-=+=ïïïîîîòòòòòòòò解得:0.6644389, 1.1584689a b »-»5、试用Legendre 多项式构造()f x x =在[-1, 3]上的二次最佳平方逼近多项式 解:作变量代换,将区间[-1, 3]变为[-1, 1],令21x t =+,即12x t -=则()()(21)21(11)F t f x f t t t ==+=+-££对()F t 利用Legendre 多项式求其在}{21,,span t t上的最佳平方逼近多项式20()()j j j S t C P t ==å,其中11(,)21()()(0,1,2)(,)2j j j j j P f j C F t P t dt j P P -+===ò20121()=1,()=t,()=(31)2P t P t P t t - 则有:1121012112111212212121215[(21)(21)]24311[(21)(21)]285(31)(31)45[(21)(21)]22264C t dt t dt C t tdt t tdt t t C t dt t dt ---------=--++==--++=--=--++=òòòòòò 01251145()()()()4864S t P t P t P t \=++则()f x 在[-1, 3]上的最佳二次逼近多项式*01222151111451()()()()()()2428264251114511=()((3()1))4826422135+82243512x x x x S t S t S P P P x x x x ----===++--++-+=7、确定一条经过原点的二次曲线,使之拟合下列数据ix123iy0.2 0.5 1.0 1.2并求平方误差2d解:设2012()1,(),()x x x x x j j j ===由题,拟合函数须过原点 则令001122()()()()f x C x C x C x j j j =++,其中00C =,即212()f x C x C x =+ 12000.2110.5,,24 1.039 1.2Y f f æöæöæöç÷ç÷ç÷ç÷ç÷ç÷===ç÷ç÷ç÷ç÷ç÷ç÷èøèøèø 11122122(,)(,)1436(,)(,)3698G f f f f f f f f æöæö==ç÷ç÷èøèø 12(,) 6.1(,)15.3Y F Y f f æöæö==ç÷ç÷èøèø得法方程GC F = 121436 6.1369815.3C C æöæöæö=ç÷ç÷ç÷èøèøèø解方程得:120.61840.0711C C »»-2()0.61840.0711f x x x \=-误差222121(,) 2.730.6184(,)0.0711(,)0.04559j j j YC Y Y Y df f f ==-=-´+´=å8、已知一组数据ix1 2 3iy3 2 1.5试用拟合函数21()S x a bx =+拟合所给数据解:令2()f x a bx =+ 201()1,()x x x j j ==01()()()f x a x b x j j =+则123113111114,219213y A F y y æöæö÷ç÷çæöç÷ç÷ç÷ç÷===ç÷ç÷ç÷ç÷èøç÷ç÷ç÷ç÷èøèøT T a A A A F b æö\=ç÷èø,即331422514983a b æöç÷æöæö=ç÷ç÷ç÷ç÷èøèøç÷èø解方程组得0.3095,0.0408a b == 即210.30950.0408()x f x y=+=从而有21()0.30950.0408S x x =+补充题:用插值极小化法求()sin f x x =在[0, 1]上的二次插值多项式2()P x ,并估计误差 解:作变量替换1(1)2x t =+,将[0, 1]变换[-1, 1]取插值点11(21)cos 0,1,2222(1)K K x K n p+=+=+ 0120.933001270.50.0669873x x x ===利用这些点做插值商表i xi y一阶插商 二阶插商0.9330127 0.80341740.5 0.479425 0.74863250.0669873 0.0659372 0.9549092 -0.23818779则:20.9330127()0.80)0.2341740.743818779(0.9330127)(0.5)86325(x P x x x ---=+-同时误差213322()()()22(1)!3!24n n M M M R x f x P x n --+=-£==+其中(3)3max ()M f x = 由于1(1)2x t =+,即21t x =- 则(3)(3)3max (21)max sin (21)8max cos(21)8[0,1]M f x x x x =-=-=-=Î281()243R x \£=。
计算图示各系统的动能:(1)偏心圆盘的质量为,偏心距OC m e =,对质心的回转半径为C ρ,绕轴O 以角速度0ω转动(图a )。
(2)长为l ,质量为的匀质杆,其端部固结半径为,质量为的匀质圆盘。
杆绕轴O 以角速度m r m 0ω转动(图b )。
(3)滑块A 沿水平面以速度移动,重块B 沿滑块以相对速度下滑,已知滑块A 的质量为,重块B 的质量为(图c )。
1v 2v 1m 2m (4)汽车以速度沿平直道路行驶,已知汽车的总质量为0v M ,轮子的质量为m ,半径为R ,轮子可近似视为匀质圆盘(共有4个轮子)(图d )。
解:(1) 222200111()222C C C T mv J m e 2ωρω=+=+(2) 2222111(83)326O J ml mr ml m l r =++=+2220011(83)212O T J m l r 22ωω==+(3) 22121122A B T m v m v =+2221121212221212221211(2cos150)2211()m v m v v v v m m v m v m v v °=+++=++(4) ()2222000211111(4)422222v T M m v mv mR M m v R ⎛⎞=−+⋅+⋅⋅=+⎜⎟⎝⎠20一常力矩M 作用在绞车的鼓轮上,轮的半径为r ,质量为。
缠在鼓轮上绳索的末端A 系一质量为的重物,沿着与水平倾斜角为1m 2m α的斜面上升,如图所示。
重物与斜面间的滑动摩擦系数为μ。
绳索的质量不计,鼓轮可看成为匀质圆柱体,开始时系统静止。
求鼓轮转过ϕ角时的角速度。
解:为一自由度理想约束系统。
取鼓轮、重物及绳索组成的系统为研究对象,受力图如下图所示。
鼓轮转过ϕ角时系统的动能为2222212111222T m r m r 2ωω=⋅⋅+ 重力、摩擦力和力矩M 在此有限路程上所做的功为122sin W M Fr m gr ϕϕϕ→α=−−根据动能定理,有()222212211sincos 42m r m r M m gr ωωαμ+=−+αϕ⎡⎤⎣⎦ ω=绞车提升一质量为m 的重物,如图所示。
第7章习题解答7—1判断题(对的打√,不对的打×)1。
数字电路分为门电路和时序逻辑电路两大类。
(× )2。
边沿触发器和基本RS触发器相比,解决了空翻的问题.(×)3. 边沿触发器的状态变化发生在CP上升沿或下降沿到来时刻,其他时间触发器状态均不变。
(√)4. 基本RS 触发器的输入端就是直接置0端和直接置1端。
(√)23 的计数器。
(×)5。
3位二进制计数器可以构成模为16。
十进制计数器最高位输出的周期是输入CP脉冲周期的10倍。
(√)7. 构成一个7进制计数器需要7个触发器。
(×)8.当时序电路存在无效循环时该电路不能自启动.( √)9。
寄存器要存放n位二进制数码时,需要n2个触发器。
(×)10.同步计数器的计数速度比异步计数器快。
(√)11。
在计数器电路中,同步置零与异步置零的区别在于置零信号有效时,同步置零还需要等到时钟信号到达时才能将触发器置零,而异步置零不受时钟的控制。
(√)12。
计数器的异步清零端或异步置数端在计数器正常计数时应置为无效状态。
(√)13。
自启动功能是任何一个时序电路都具有的。
(× )14。
无论是用置零法还是用置数法来构成任意N进制计数器时,只要置零或置数控制端是异步的,则在状态循环过程中一定包含一个过渡状态;只要是同步的,则不需要过渡状态。
(√)15。
用置零法或置位法可以设计任意进制的计数器.(×)7—2 由或非门组成的基本RS触发器如图7—38所示,已知R、S的电压波形,试画出与之对应的Q和Q的波形。
图7—38 题7-2图解:由或非门组成的基本RS触发器的特性表,可得该题的输出端波形如下图所示:或非门RS 触发器特性表 题7—2 波形图7—3由与非门组成的基本RS 触发器如图7-39所示,已知R 、S 的电压波形,试画出与之对应的Q 和Q 的波形。
图7-39 题7-3图解:由与非门组成的基本RS 触发器的特性表,可得该题的输出端波形如下图所示:与非门RS 触发器特性表 题7—3波形图7-4已知如图7-40所示的各触发器的初始状态均为0,试对应画出在时钟信号CP 的连续作用下各触发器输出端Q 的波形。
第七章群体心理与群体行为思考题1.在群体中,如何加强对非正式群体的引导和利用?答:加强对非正式群体的引导和利用,对非正式群体进行有效的管理主要有以下三种途径:(1)管理者自觉加强与非正式群体的联系。
管理者应该深入到员工中去,了解他们的思想、工作和生活状况;了解非正式群体领袖的个性、能力及态度,做到心中有数,与非正式群体领袖积极沟通,必要时理解、参与和支持非正式群体的有益活动。
(2)运用舆论导向引导。
运用企业的舆论工具、媒体、事件等,对非正式组织的群体成员进行有目的、有计划的引导,循序渐进地使非正式群体成员的意见与企业的组织目标相一致。
此外,为非正式群体成员提供交流、沟通的机会,如各种舞会、联欢会、恳谈会、旅游、聚餐等,让他们潜移默化地逐步接受企业的观点。
(3)区别对待不同类型的非正式群体。
针对不妨碍组织目标的群体比如说友谊型群体,可以将其纳入到管理中来,提高员工的情感承诺,增强组织支持感;针对可能妨碍组织目标的群体比如说利益型群体,首先要制定相应的制度,防止其对组织利益的侵害;其次要对非正式群体加以疏导利用,使其行为符合组织规范。
同时管理者要团结并发挥非正式群体领袖的作用,引导非正式群体目标与正式群体目标相一致;针对个别不利于组织目标的群体如破坏型群体,在说服引导无效后应采取措施予以拆散。
2.从众行为是怎样产生的?受哪些因素影响?答:(1)从众行为产生的原因主要有两点。
一是行为参照。
根据社会比较理论,在情景不确定的情况下,他人的行为最具有参照价值。
多数人一致的行为往往构成了一个最可靠的参照系统,人们根据这个参照系统做出自己的行为表现,这就是从众。
二是对偏离的恐惧。
个体偏离群体、标新立异的行为往往会受到群体的压力甚至遭受惩罚。
研究表明,群体总是喜欢和接受与群体一致的成员,厌恶、拒绝甚至制裁偏离群体的成员。
(2)影响因素主要有以下四个方面:①情景的确定性程度。
当情景越明朗的时候,个体越不容易从众。
当个体对标准答案越肯定时越倾向于坚持自己的意见,不服从集体的错误结论。
第7章思考题及习题71.如果采用的晶振的频率为24MHz,定时器/计数器工作在方式0、1、2下,其最大定时时间各为多少?答:晶振的频率为24MHz, 机器周期为0.5µs。
方式0最大定时时间=0.5µs×213=0.5µs×8192=4096µs方式1最大定时时间=0.5µs×216=0.5µs×65536=327686µs方式2最大定时时间=0.5µs×28=0.5µs×256=128µs2.定时器/计数器用作计数器模式时,对外界计数频率有何限制?答:外部输入的计数脉冲的最高频率为系统振荡器频率的1/24。
3.定时器/计数器的工作方式2有什么特点?适用于哪些应用场合?答:方式2为初值自动装入的8位定时器/计数器,克服了在循环定时或循环计数应用时就存在用指令反复装入计数初值影响定时精度的问题。
4.TH x与TL x(x= 0,1)是普通寄存器还是计数器?其内容可以随时用指令更改吗?更改后的新值是立即刷新还是等当前计数器计满后才能刷新?答:THx与TLx(x = 0,1)是计数器,其内容可以随时用指令更改,但是更改后的新值要等当前计数器计满后才能刷新。
5.Proteus虚拟仿真使用定时器T0,采用方式2定时,在P1.0脚输出周期为400µs,占空比为4:1的矩形脉冲,要求在P1.0脚接有虚拟示波器,观察P1.0脚输出的矩形脉冲波形。
答:略6.Proteus虚拟仿真利用定时器T1的中断来使P1.7控制蜂鸣器发出1kHz的音频信号,假设系统时钟频率为12MHz。
答:利用定时器T1的中断控制P1.7引脚输出频率为1kHz的方波音频信号,驱动蜂鸣器发声。
系统时钟为12MHz。
方波音频信号的周期为1ms,因此T1的定时中断时间为0.5 ms,进入中断服务程序后,对P1.7求反。
电路如图所示。
图控制蜂鸣器发出1kHz的音频信号先计算T1初值,系统时钟为12MHz,则方波的周期为1µs。
1kHz的音频信号周期为1ms,要定时计数的脉冲数为a。
则T1的初值:TH1=(65 536−a)/256;TL1=(65 536−a) %256参考程序如下:#include<reg51.h> //包含头文件sbit sound=P1^7; //将sound位定义为P1.7引脚#define f1(a) (65536-a)/256 //定义装入定时器高8位的时间常数#define f2(a) (65536-a)%256 //定义装入定时器低8位的时间常数unsigned int i = 500;unsigned int j = 0;void main(void){EA=1; //开总中断.ET1=1; //允许定时器T1中断 .TMOD=0x10; //TMOD=0001 000B,使用T1的方式1定时TH1=f1(i); //给定时器T1高8位赋初值.TL1=f2(i); //给定时器T1低8位赋初值.TR1=1; //启动定时器T1while(1){ //循环等待i=460;while(j<2000);j=0;i=360;while(j <2000);j=0;}}void T1(void) interrupt 3 using 0 //定时器T1中断函数{TR1= 0; //关闭定时器T1sound=~sound; //P1.7输出求反TH1=f1(i); //定时器T1的高8位重新赋初值.TL1=f2(i); //定时器T1的低8位重新赋初值.j++;TR1=1; //启动定时器T1}7. Proteus虚拟仿真制作一个LED数码管显示的秒表,用2位数码管显示计时时间,最小计时单位为“百毫秒”,计时范围0.1~9.9s。
当第1次按下并松开计时功能键时,秒表开始计时并显示时间;第2次按下并松开计时功能键时,停止计时,计算两次按下计时功能键的时间,并在数码管上显示;第3次按下计时功能键,秒表清0,再按1次计时功能键,重新开始计时。
如果计时到9.9s时,将停止计时,按下计时功能键,秒表清零,再按下重新开始计时。
答:本秒表应用了AT89C51的定时器工作模式,计时范围0.1~9.9s。
此外还涉及如何编写控制LED数码管显示的程序。
LED数码管显示的秒表原理电路如图所示。
图 LED数码管显示的秒表原理电路及仿真参考程序如下:#include<reg51.h> //包含51单片机寄存器定义的头文件unsigned char code discode1[]={0xbf,0x86,0xdb,0xcf,0xe6,0xed,0xfd,0x87,0xff,0xef};//数码管显示0~9的段码表, 带小数点unsigned char code discode2[]={0x3f,0x06,0x5b,0x4f,0x66,0x6d,0x7d,0x07,0x7f,0x6f};//数码管显示0~9的段码表,不带小数点unsigned char timer=0; //记录中断次数unsigned char second; //储存秒unsigned char key=0; //记录按键次数main() //主函数{TMOD=0x01; //定时器T0方式1定时ET0=1; //允许定时器T0中断EA=1; //总中断允许second=0; //设初始值P0=discode1[second/10]; //显示秒位0P2=discode2[second%10]; //显示0.1s位0while(1) //循环{if((P3&0x80)==0x00) //当按键被按下时{key++; //按键次数加1switch(key) //根据按键次数分三种情况{case 1: //第一次按下为启动秒表计时TH0=0xee; //向TH0写入初值的高8位TL0=0x00; //向TL0写入初值的低8位,定时5msTR0=1; //启动定时器T0break;case 2: //按下两次暂定秒表TR0=0; //关闭定时器T0break;case 3: //按下3次秒表清0key=0; //按键次数清0second=0; //秒表清0P0=discode1[second/10]; //显示秒位0P2=discode2[second%10]; //显示0.1s位0break;}while((P3&0x80)==0x00); //如果按键时间过长在此循环}}}void int_T0() interrupt 1 using 0 //定时器T0中断函数{TR0=0; //停止计时,执行以下操作(会带来计时误差)TH0=0xee; //向TH0写入初值的高8位TL0=0x00; //向TL0写入初值的低8位,定时5mstimer++; //记录中断次数if (timer==20) //中断20次,共计时20*5ms=100ms=0.1s{timer=0; //中断次数清0second++; //加0.1sP0=discode1[second/10]; //根据计时时间,即时显示秒位P2=discode2[second%10]; //根据计时时间,即时显示0.1s位}if(second==99) //当计时到9.9s时{TR0=0; //停止计时second=0; //秒数清0key=2; //按键数置2,当再次按下按键时,key++,即key=3,秒表清0复原}else //计时不到9.9s时{TR0=1; //启动定时器继续计时}}8. Proteus虚拟仿真制作一个采用LCD1602显示的电子钟,在LCD上显示当前的时间。
显示格式为“时时:分分:秒秒”。
设有4个功能键k1~k4,功能如下:(1)k1—进入时间修改。
(2)k2—修改小时,按一下k2,当前小时增1。
(3)k3—修改分钟,按一下k3,当前分钟增1。
(4)k4—确认修改完成,电子钟按修改后的时间运行显示。
答:本题难点在于处理功能键K1~K4的输入,由于每个功能键都具有相应的一种或多种功能,因此程序中需要大量使用do{}while或while{}循环结构,以检测是否有按键按下的具体功能。
按键检测函数如下:void time_change(){unsigned char keyvalue0=0,keyvalue1=0;keyvalue0=keyscan();//检测是否有按键按下if(keyvalue0)//如果有按键按下,继续检测{if(keyvalue0==1)//按键1,走时停止,开始判断更改值,直到按键4按下{while(~key0);//防抖,直到按键松开时才进行下一步的操作TR0=0;//控制走时的中断停止do{keyvalue1=keyscan();//检测按键按下if(keyvalue1==2)//如果按键2按下,改变时间{while(~key1);//防抖if(hour<23)//如果小时数小于23则加1{hour++;}else//如果小时数为23,置位为0{hour=0;}}else if(keyvalue1==3)//如果按键3按下,改变分钟{while(~key2);//防抖if(minute<59)//如果分钟数小于59则加1{minute++;}else//如果分钟数为59,置位为0{minute=0;}clock_write();}}while(keyvalue1!=4);//重复对时间的修改直到按键4按下while(~key3==0);//防抖TR0=1;//调整时间后重新开始走时}}}必须注意,程序设计中,小时、分钟、秒变量hour、minute、second必须置为全局变量,才能如上述函数一样在各处函数中直接进行修改,如为局部变量,则上述形式的直接修改无效。
1602 液晶显示模块以及基于单片机定时器的时钟实现见教材的介绍,不再赘述。
LCD时钟原理电路图如下图。
程序执行后工作指示灯D1闪动一下,表示时钟开始运行。
按下按键K1后,D1停止闪烁,即时钟停止走时,时钟停在当前时刻;按下按键K2和K3后,可改变小时和分钟;按下按键K4后,时钟从修改后的时间重新开始运行。
为加强AT89C51的驱动能力,原理图中加入作为上拉电阻的排电阻(CTRESPACK-7),即图中的RP1。
图 LCD电子钟电路原理电路图与仿真。