自控原理(7)

807自动控制原理自动控制原理是现代控制工程中的重要理论基础，它是控制工程中的核心内容之一。

自动控制原理主要研究如何利用控制器对被控对象进行自动调节，使其输出符合预期的要求。

在工业生产、航空航天、交通运输等领域，自动控制原理都有着广泛的应用。

首先，自动控制原理的基本概念是控制系统。

控制系统由输入、输出、控制器和被控对象组成。

输入是控制系统接受的外部指令或信号，输出是控制系统产生的响应信号，控制器是控制系统的核心部分，它根据输入信号和输出信号之间的差异来调节被控对象，使其输出符合预期的要求。

其次，自动控制原理的核心内容是反馈控制。

反馈控制是指控制系统根据被控对象的输出信号对输入信号进行调节的一种控制方式。

通过不断地比较被控对象的实际输出和期望输出，控制系统可以及时地调整控制器的工作状态，使被控对象的输出逐渐接近期望输出。

另外，自动控制原理还涉及到控制系统的稳定性分析。

控制系统的稳定性是指当控制系统受到外部干扰时，系统是否能够快速地恢复到稳定状态。

稳定性分析是控制系统设计中的重要环节，它可以帮助工程师评估控制系统的性能，并对系统进行优化设计。

此外，自动控制原理还包括控制系统的性能指标。

控制系统的性能指标通常包括超调量、调节时间、静差等。

这些指标可以帮助工程师评估控制系统的性能，指导控制系统的设计和调节。

最后，自动控制原理还涉及到控制系统的设计方法。

控制系统的设计方法包括传统的PID控制、模糊控制、神经网络控制、自适应控制等。

不同的设计方法适用于不同的控制对象和控制要求，工程师需要根据实际情况选择合适的设计方法。

总之，自动控制原理是现代控制工程中的重要理论基础，它涉及到控制系统、反馈控制、稳定性分析、性能指标和设计方法等内容。

掌握自动控制原理对于工程师来说至关重要，它可以帮助工程师设计高性能的控制系统，提高工业生产的效率和质量，推动科技进步和社会发展。

自动控制理论是研究自动控制共同规律的技术科学。

它的发展初期，是以反馈理论为基础的自动调节原理，主要用于工业控制，二战期间为了设计和制造飞机及船用自动驾驶仪，火炮定位系统，雷达跟踪系统以及其他基于反馈原理的军用设备，进一步促进并完善了自动控制理论的发展。

到战后，以形成完整的自动控制理论体系，这就是以传递函数为基础的经典控制理论，它主要研究单输入-单输出，线形定常数系统的分析和设计问题。

20世纪60年代初期，随着现代应用数学新成果的推出和电子计算机的应用，为适应宇航技术的发展，自动控制理论跨入了一个新阶段——现代控制理论。

他主要研究具有高性能，高精度的多变量变参数的最优控制问题，主要采用的方法是以状态为基础的状态空间法。

目前，自动控制理论还在继续发展，正向以控制论，信息论，仿生学为基础的智能控制理论深入。

为了实现各种复杂的控制任务，首先要将被控制对象和控制装置按照一定的方式连接起来，组成一个有机的总体，这就是自动控制系统。

在自动控制系统中，被控对象的输出量即被控量是要求严格加以控制的物理量，它可以要求保持为某一恒定值，例如温度，压力或飞行航迹等；而控制装置则是对被控对象施加控制作用的机构的总体，它可以采用不同的原理和方式对被控对象进行控制，但最基本的一种是基于反馈控制原理的反馈控制系统。

在反馈控制系统中，控制装置对被控装置施加的控制作用，是取自被控量的反馈信息，用来不断修正被控量和控制量之间的偏差从而实现对被控量进行控制的任务，这就是反馈控制的原理。

同时自动控制原理也是现在高校自动化专业的一门主干课程，是学习后续专业课的重要基础，也是自动化专业硕士研究生入学必考的专业课。

该课不仅是自动控制专业的基础理论课，也是其他专业的基础理论课，目前信息科学与工程学院开设本课程的专业有计算机、电子信息、检测技术。

该课程不仅跟踪国际一流大学有关课程内容与体系，而且根据科研与学术的发展不断更新课程内容，从而提高自动化及相关专业的整体学术水平。

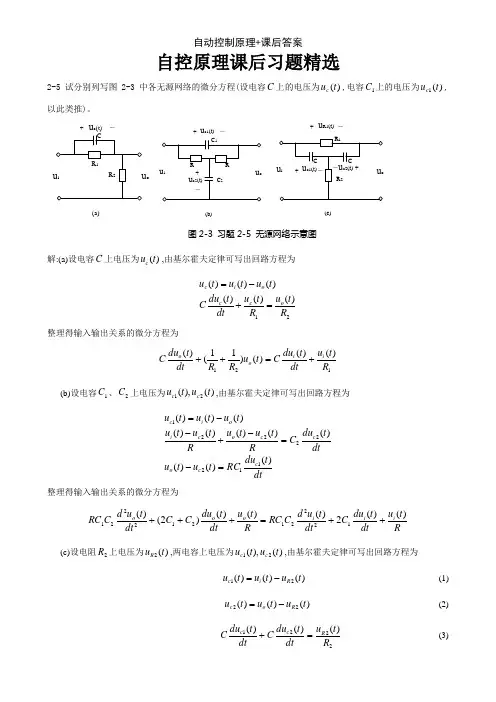
普通高等教育“十一五”国家级规划教材全国高等专科教育自动化类专业规划教材《自动控制原理》习题答案主编：陈铁牛机械工业出版社1-11-21-3闭环控制系统主要由被控对象，给定装置，比较、放大装置，执行装置，测量和变送装置，校正装置等组成。

被控对象：指要进行控制的设备和过程。

给定装置：设定与被控量相对应给定量的装置。

比较、放大装置：对给定量与测量值进行运算，并将偏差量进行放大的装置。

执行装置：直接作用于控制对象的传动装置和调节机构。

测量和变送装置：检测被控量并进行转换用以和给定量比较的装置。

校正装置：用以改善原系统控制性能的装置。

题1-4答：（图略）题1-5答：该系统是随动系统。

（图略）题1-6答：（图略）题2-1 解：（1）F(s)=12s 1+-Ts T（2）F(s)=0.5)421(2+-s s（3）F(s)=428+⋅s es sπ（4）F(s)=25)1(12+++s s（5）F(s)=32412ss s ++ 题2-2 解：(1) f(t)=1+cost+5sint (2) f(t)=e -4t(cost-4sint)(3) f(t)=t t t te e e 101091811811----- (4) f(t)= -tt t te e e ----+-3118195214(5) f(t)= -tt e e t 4181312123--+++题2-3 解：a)dtdu u C R dt du R R c c r 22111=++）（ b)r c c u CR dt du R R u C R dt du R R 1r 12112111+=++）（ c) r r r c c c u dtdu C R C R dtu d C C R R u dtdu C R C R C R dtu d C C R R +++=++++）（）（1211222121122111222121 题2-4 解：a) G(s)=1)(212++s T T sT (T 1=R 1C, T 2=R 2C )b) G(s)=1)(1212+++s T T s T (T 1=R 1C, T 2=R 2C )c) G(s)= 1)(1)(32122131221+++++++s T T T s T T s T T s T T (T 1=R 1C 1, T 2=R 1C 2, T 3=R 2C 1, T 4=R 2C 2 )题2-5 解：(图略)题2-6 解：33)(+=Φs s 题2-7 解：a) ksf ms s +-=Φ21)(b) )()()(1))(1)(()(21221s G s G s G s G s G s +++=Φc) )()(1)())()(()(31321s G s G s G s G s G s ++=Φd) )()()()(1))()()(323121s G s G s G s G s G s G s -+-=Φe) G(s)=[G 1(s)- G 2(s)]G 3(s)f) )()()()()()()()()()(1)()()()()(43213243214321s G s G s G s G s G s G s G s G s G s G s G s G s G s G s +-++=Φg) )()()()()()()()(1)()()()(43213212321s G s G s G s G s G s G s G s G s G s G s G s -+-=Φ题2-8 解：102310)1()()(k k s s T Ts k k s R s C ⋅++++⋅=1023101)1()()(k k s s T Ts k k s N s C ⋅++++⋅=1023102)1()()(k k s s T Ts s T k k s N s C ⋅++++⋅⋅⋅= 题2-9 解：)()()()(1)()()(4321111s G s G s G s G s G s R s C +=)()()()(1)()()(4321222s G s G s G s G s G s R s C +=)()()()(1)()()()()(432142121s G s G s G s G s G s G s G s R s C +=)()()()(1)()()(4321412s G s G s G s G s G s R s C += 题2-10 解：(1)3212321)()(k k k s k k k s R s C +=3212032143)()()(k k k s s G k k k s k k s N s C +⋅+= (2) 2140)(k k sk s G ⋅-= 题2-11 解：122212211111)()1()()(z z s T s T T C s T T s T k k s s m m d e L ⋅++⋅+++⋅=ΘΘ (T 1=R 1C, T 2=R 2C, T d =L a /R a , T m =GD 2R a /375C e C m )第三章 习题答案3-1． s T 15=（取5%误差带） 3-2． 1.0=H K K=2 3-3．当系统参数为：2.0=ξ，15-=s n ω时，指标计算为：%7.52%222.0114.32.01===-⨯---e eξξπσs t ns 352.033=⨯==ξωs t n p 641.02.01514.3122=-⨯=-=ξωπ当系统参数为：0.1=ξ，15-=s n ω时，系统为临界阻尼状态，系统无超调，此时有：st ns 95.057.10.145.67.145.6=-⨯=-=ωξ3-4．当110-=s K 时，代入上式得：110-=s n ω，5.0=ξ，此时的性能指标为：%3.16%225.0114.35.01===-⨯---e eξξπσs t ns 6.0105.033=⨯==ξωs t n p 36.05.011014.3122=-⨯=-=ξωπ当120-=s K 时，代入上式得：11.14-=s n ω，35.0=ξ，此时的性能指标为：%5.30%2235.0114.335.01===-⨯---e eξξπσs t ns 6.01.1435.033=⨯==ξω由本题计算的结果可知：当系统的开环放大倍数增大时，其阻尼比减小，系统相对稳定性变差，系统峰值时间变短，超调量增大，响应变快，但由于振荡加剧，调节时间不一定短，本题中的调节时间一样大。

自动控制原理
自动控制原理是一门研究如何通过控制器使系统自动实现某种期望状态或行为的学科。

在自动控制原理中，我们关注的是如何设计控制器，使得系统能够根据输入信号和反馈信号自动调节输出信号，以达到所期望的控制目标。

在自动控制原理中，常用的控制器有比例控制器、积分控制器和微分控制器。

比例控制器根据输入信号和反馈信号的差异比例调节输出信号。

积分控制器则通过将输入信号和反馈信号的累积误差积分起来，来调节输出信号。

微分控制器则通过计算输入信号和反馈信号的变化率，来调节输出信号。

在自动控制原理中，我们还关注系统的稳定性和动态响应。

稳定性是指系统在无干扰情况下，输出信号是否趋于稳定。

动态响应则是指系统在面对外部干扰或输入信号变化时，输出信号的变化情况。

通过分析系统的稳定性和动态响应行为，我们可以对系统进行优化和改进，以使其更好地满足控制要求。

除了常规的反馈控制方式，自动控制原理还包括了前馈控制和模糊控制等技术。

前馈控制是指根据已知输入信号的特征，提前对系统进行补偿，以减小系统的误差和响应时间。

模糊控制则是一种基于模糊逻辑的控制手段，它可以处理一些模糊信息和不确定性信息，使系统能够根据不完全准确的输入信号做出相对准确的控制决策。

总结来说，自动控制原理是一门研究系统如何通过控制器自动调节和控制输出信号的学科。

它涉及了控制器的设计、系统的
稳定性和动态响应分析，以及一些先进的控制技术。

通过应用自动控制原理，我们能够提高系统的效率、稳定性和可靠性，实现自动化控制，从而在工业和生活中发挥重要作用。

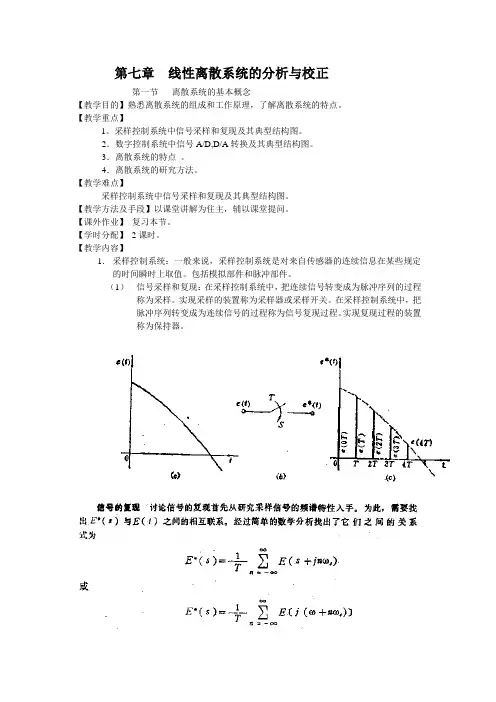
第七章线性离散系统的分析与校正第一节离散系统的基本概念【教学目的】熟悉离散系统的组成和工作原理，了解离散系统的特点。

【教学重点】1。

采样控制系统中信号采样和复现及其典型结构图。

2．数字控制系统中信号A/D,D/A转换及其典型结构图。

3．离散系统的特点。

4．离散系统的研究方法。

【教学难点】采样控制系统中信号采样和复现及其典型结构图。

【教学方法及手段】以课堂讲解为住主，辅以课堂提问。

【课外作业】复习本节。

【学时分配】2课时。

【教学内容】1．采样控制系统：一般来说，采样控制系统是对来自传感器的连续信息在某些规定的时间瞬时上取值。

包括模拟部件和脉冲部件。

（1）信号采样和复现：在采样控制系统中，把连续信号转变成为脉冲序列的过程称为采样。

实现采样的装置称为采样器或采样开关。

在采样控制系统中，把脉冲序列转变成为连续信号的过程称为信号复现过程。

实现复现过程的装置称为保持器。

（2）采样控制系统的典型结构图。

见书本273页图7-4。

2．．数字控制系统：是一种以数字计算机为控制器去控制具有连续的工作状态的被控对象的闭环控制系统。

包括数字计算机和被控对象两部分。

其典型结构图。

见书本276页图7-9。

3．离散系统的特点：（1）由数字计算机构成的数字校正装置，效果比连续式校正装置好，而且由软件实现的控制规律容易改变，控制灵活。

（2）采样信号，特别是数字信号的传递可以有效抑制噪音，从而提高系统的抗干扰能力。

（3）容许采用高灵敏度的控制元件，以提高系统的控制精度。

（4）可以用一台计算机分时控制若干系统，提高了设备的利用率，经济性好。

（5）对于具有传输延迟，特别是大延迟系统，可以引入采样的方式稳定。

【自学内容】预习第二节信号的采样与保护。

第二节信号的采样与保护【教学目的】1。

了解采样器。

2．采样定理和采样信号的恢复。

3．零阶保持器【教学重点】采样定理和采样信号的恢复。

【教学难点】采样定理和采样信号的恢复【教学方法及手段】以课堂讲解为住主，辅以课堂提问。

第七章7-1 什么是非线性系统？它是什么特点？7-2 常见的非线性特征有哪些？7-3 非线性系统的分析设计方法有哪些？7-4 描述函数分析法的实质是什么？试描述函数的概念及其求取方法。

7-5 试述相平面分析法的实质。

为什么它是分析二阶系统的有效方法？7-6 试确定3xy表示的非线性元件的描述函数。

7-7 一放大装置的非线性特性示于图p7-1，求其描述函数。

7-8 图p7-2为变放大系数非线性特征，求其描述函数。

7-9 求图p7-3所示非线性环节的买书函数。

7-10 某死区非线性特性如图p7-4所示，试画出该环节在正弦输入下的输出波形，并求出其描述函数N{A}。

7-11 图p7-5给出几个非线性特性。

试分别写出其基准描述函数公式，并正在复平面上大致画出其基准描述函数的负倒数特性》7-12 判断图p7-6所示各系统是否稳定？-1/N。

与K。

W(jw)的交点是稳定工作点还是不稳定工作点？解：（a）是稳定工作点（b）是稳定工作点（c）a点不是稳定工作点b点是稳定工作点（d）不是稳定工作点（e）是稳定工作点7-13 图p7-7所示为继电器控制系统的结构图，其线性部分的传递函数为 )11.0)(15.0)(1(10)(+++=s s s s W 试确定自持振荡的角频率和振幅。

解：该系统非线性部分为具有滞环的两位置继电器，其描述函数为（见教材P343 公式（7-25））：)(414)(22h A A Mh jA h A M A N ≥-⎪⎭⎫⎝⎛-=ππ则)(414141*********)(1222222222h A M h j A h M A A h j A h M A A h A h A h jA h M A A h j A h A h j A h A h jA h M AA h jA h MAA N ≥-⎪⎭⎫ ⎝⎛--=⎪⎪⎭⎫ ⎝⎛+⎪⎭⎫ ⎝⎛--=⎪⎭⎫⎝⎛+⎪⎭⎫ ⎝⎛-+⎪⎭⎫⎝⎛--=⎪⎪⎭⎫ ⎝⎛+⎪⎭⎫ ⎝⎛-⎪⎪⎭⎫ ⎝⎛-⎪⎭⎫ ⎝⎛-+⎪⎭⎫⎝⎛--=-⎪⎭⎫⎝⎛-=-ππππππ由图可得：2=M ，1=h 代入到)(1A N -中，)(8118)(12h A j A A A N ≥-⎪⎭⎫ ⎝⎛--=-ππ线性部分相频为：)1.01)(5.01)(1()05.06.165.01(10)1.01)(5.01)(1()1.01)(5.01)(1(10)1.01)(5.01)(1)(11.0)(15.0)(1()1.01)(5.01)(1(10)11.0)(15.0)(1(10)(222223222222ωωωωωωωωωωωωωωωωωωωωωωωωω+++---=+++---=---+++---=+++=j j j j j j j j j j j j j j j j j j W因为)(ωj W 曲线与)(1A N -曲线相交，则虚部8)1.01)(5.01)(1(5.016222223πωωωωωj j j -=+++--即8)1.01)(5.01)(1(5.016222223πωωωωω=++++ ωωωωω2832.6194.0126.12625.00025.03246+=+++即012832.626.1194.02625.00025.02346=+-+-+ωωωωω 解上述方程得到：1645.01=ω，4256.22=ω00198.1494.07.434.91645.01.0arctan 1645.05.0arctan 1645.0arctan )(-=---=⨯-⨯--=ωϕ显然不符合题义。

自控原理
自控原理是指在一个系统中，通过设定目标、监测实际状况，然后通过反馈来对系统进行调整，以使系统能够自我调节、自我控制的一种原理。

自控原理被广泛运用于许多领域，如工程控制系统、生态系统、经济系统等。

自控原理在工程控制系统中的应用
在工程控制系统中，自控原理起着至关重要的作用。

工程控制系统是指通过传感器获取系统的状态信息，然后通过执行器对系统进行控制，以实现系统的预期目标。

自控原理在工程控制系统中的应用可以帮助系统实现自动化控制，提高系统的稳定性和效率。

自控原理在生态系统中的应用
生态系统是一个复杂的系统，包括了许多生物和非生物组成部分。

在生态系统中，自控原理可以帮助系统自我调节，保持生态平衡。

例如，生物通过自觉的选择食物和生存环境，以维持生态系统的稳定性。

同时，自控原理也可以帮助人类更好地保护和管理生态系统，以实现人与自然的和谐共生。

自控原理在经济系统中的应用
在经济系统中，自控原理可以帮助企业实现自我调节和自我控制。

通过设定目标、监测市场状况，企业可以及时调整经营策略，提高竞争力。

同时，政府也可以通过自控原理来制定经济政策，以促进经济的稳定增长。

综上所述，自控原理作为一种普遍适用的原理，可以帮助系统实现自我调节、自我控制，提高系统的稳定性和效率。

通过深入理解和运用自控原理，我们可以更好地管理和优化各种系统，实现系统的良性发展。