下载文档原格式
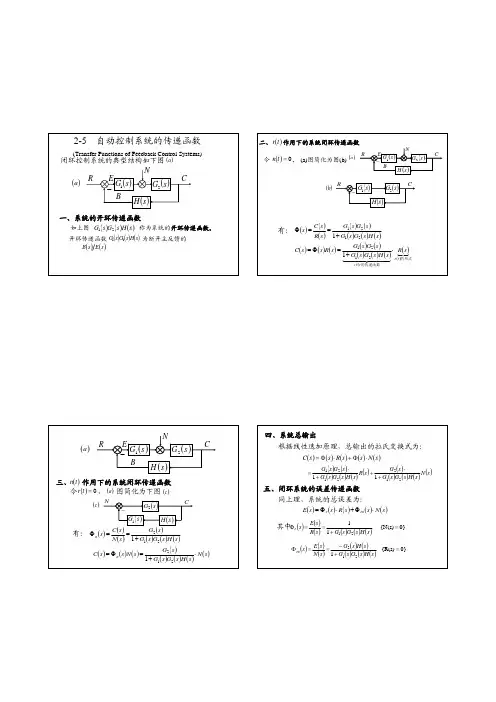
2-5 自动控制系统的传递函数(Transfer Functions of Feedback Control Systems)()s G 1()s H ()s G 2NRBCE−()a 闭环控制系统的典型结构如下图()a 一、系统的开环传递函数如上图称为系统的开环传递函数。
()()()s H s G s G 21开环传递函数为断开主反馈的()()()s H s G s G 21()()s E s B 二、作用下的系统闭环传递函数()t r ()s G 1()s H ()s G 2RC−()b 令, (a)图简化为图(b)()0=t n ()s G 1()s H ()s G 2NRBCE−()a 有：()()()()()()()()s H s G s G s G s G s R s C s 21211+==Φ()()()()()()()()()(){的形式的传递函数对t r r c s R s H s G s G s G s G s R s s C ⋅+=Φ=44434442121211三、作用下的系统闭环传递函数()t n ()a ()c 令，图简化为下图()0=t r ()s G 2()s G 1()s H NC−()c 有：()()()()()()()s H s G s G s G s N s C s n 2121+==Φ()()()()()()()()s N s H s G s G s G s N s s C n ⋅+=Φ=2121()s G 1()s H ()s G 2N RBCE−()a 四、系统总输出根据线性迭加原理，总输出的拉氏变换式为：()()()()()s N s s R s s C ⋅Φ+⋅Φ=()()()()()()()()()()()s N s H s G s G s G s R s H s G s G s G s G 212212111+⋅++⋅=五、闭环系统的误差传递函数同上理，系统的总误差为：()()()()()s N s s R s s E en e ⋅Φ+⋅Φ=()()()()()()0}{N(s) 1121=+==Φs H s G s G s R s E s e 其中：()()()()()()()()0}{R(s) 1212=+−==Φs H s G s G s H s G s N s E s en本章要点•传递函数概念？•怎样建立系统的传递函数？•结构图等效变换、梅森公式作业•2-4•2-5•2-6•在计算机上实现2-6节:MATLAB的应用。
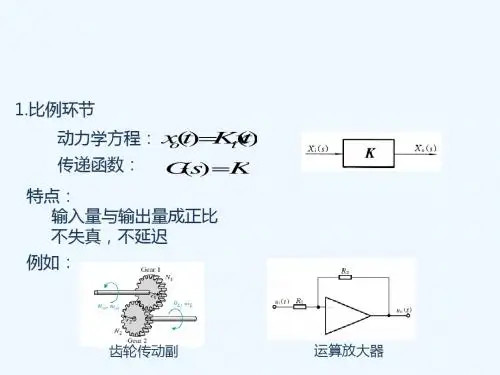
自动控制原理传递函数在自动控制系统中，传递函数是一种常用的描述系统动态性能的数学工具。
它反映了系统的输入信号与输出信号之间的关系。
传递函数常用于描述线性、时不变系统，并且在控制系统设计中有着重要的作用。
传递函数可以通过系统的微分方程求得。
对于一个一阶系统，其微分方程一般可以表示为：dy(t)/dt = K*u(t)其中，dy(t)/dt表示系统的输出变量的变化率，K表示系统的增益，u(t)表示系统的输入变量。
通过对上述微分方程进行拉普拉斯变换，可以得到对应的传递函数：Y(s)=K*U(s)/s在上式中，s表示复数变量，Y(s)和U(s)分别表示输出信号和输入信号的拉普拉斯变换。
通过传递函数，我们可以方便地分析系统的动态性能。
传递函数是控制系统设计中的重要工具，它具有以下几个特点：1.表征系统的动态性能：传递函数通过描述输入信号和输出信号之间的关系，反映了系统的动态响应特性。
通过分析传递函数的特性，可以预测系统的稳定性、阻尼性、超调量等重要性能指标。
2.方便进行频域分析：传递函数在频域中有简洁的表达形式，可以方便地进行频域分析。
通过对传递函数进行频率响应分析，可以确定系统的频率特性，为系统的设计和调整提供依据。
3.便于系统设计和优化：传递函数可以直观地表示系统的输入输出关系，便于系统设计和性能调整。
通过对传递函数进行变换和运算，可以方便地进行系统的设计和优化。
可以通过一些常见的传递函数来说明其作用。
以二阶系统为例，其一般传递函数形式为：G(s) = K/(s^2 + 2ξωns + ωn^2)其中，K为系统的增益，ξ为系统的阻尼比，ωn为系统的固有频率。
通过对传递函数的分析，可以得到系统的阶跃响应、频率响应和单位冲激响应等重要特性。
总之，传递函数在自动控制原理中是一种重要的数学工具，通过它可以方便地描述和分析系统的动态特性。
掌握传递函数的分析方法，对于控制系统的设计和优化具有重要的指导意义。
对于自动控制原理的学习和应用，传递函数的掌握是非常重要的一部分。
