医学统计学(贺生,刘元元,晏志勇)思维导图

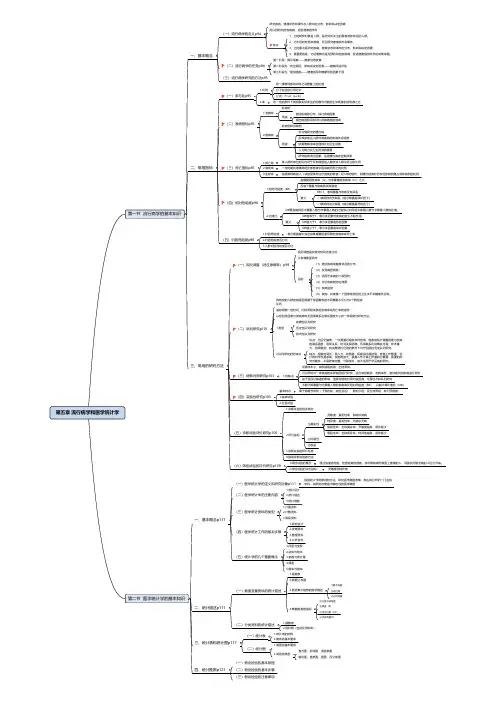
第五章 流行病学和医学统计学第一节 流行病学的基本知识一、基本概念（一）流行病学的定义p94研究疾病、健康状态和事件在人群中的分布、影响和决定因素用以预防和控制疾病，促进健康的学科特点：1、它的研究对象是人群，是研究所关注的具有某种特征的人群。

2、它不仅研究各种疾病，而且研究健康状态和事件。

3、它的重点是研究疾病、健康状态和事件的分布、影响和决定因素。

4、最重要的是，它的落脚点是为预防和控制疾病，促进健康提供科学的决策依据。

（二）流行病学的任务p94第一阶段：揭示现象——健康信息收集第二阶段为“找出原因、影响或决定因素——健康风险评估第三阶段为“提供措施——健康指导和健康危险因素干预（三）流行病学研究的方法p95二、常用指标（一）率与比p951.比例同一事物局部和总体之间数量上的比值分子包含在分母之中公式：P=a/（a+b）2.率在一定的条件下某现象实际发生的例数与可能发生该现象的总例数之比（二）发病指标p951.发病率新病例用途描述疾病的分布，探讨发病因素提出病因假设和评价防御措施的效果2.患病率新病例和旧病例用途：针对病程长的慢性病反映某地区人群对某疾病的疾病负担程度依据患病率来合理地计划卫生设施人力物力及卫生资源的需要研究疾病流行因素，监测慢性病的控制效果（三）死亡指标p971.死亡率某人群在单位时间内死于所有原因的人数在该人群中所占的比例2.病死率一定时期内患某病的全部患者中因该病而死亡的比例3.生存率指患某种病的人（或接受某种治疗措施的患者）经n年的随访，到随访结束时仍存活的病例数占观察病例的比例（四）相对危险度p981.相对危险度（RR）指暴露组发病率（Ie）与非暴露组发病率（Io）之比反映了暴露与疾病的关联强度意义：RR=1，表明暴露与疾病没有关系<1表明存在负联系（提示暴露是保护因子）>1表明存在正联系（提示暴露是危险因子）2.比值比OR要指病例组中暴露人数与非暴露人数的比值除以对照组中暴露人数与非暴露人数的比值。

图文《医学统计学》PPT课件目录•医学统计学概述•医学统计学基本概念•描述性统计方法•推断性统计方法•实验设计与分析•临床医学中的统计学应用01医学统计学概述定义与特点定义医学统计学是应用数理统计学的原理和方法，在医学领域中研究数据的收集、整理、分析和解释的一门科学。

特点以医学为背景，以数据为基础，运用统计学方法揭示医学现象的数量特征和规律。

发展历程及现状发展历程医学统计学经历了从描述性统计到推断性统计，再到现代多元统计分析的发展历程。

现状随着计算机技术的发展和大数据时代的到来，医学统计学在医学研究和实践中发挥着越来越重要的作用。

研究对象与任务研究对象医学统计学的研究对象包括生物医学数据、临床医学数据、公共卫生数据等。

任务医学统计学的任务包括描述医学数据的分布特征、比较不同组别间的差异、分析影响医学现象的因素、预测医学现象的发展趋势等。

02医学统计学基本概念总体样本样本量从总体中随机抽取的一部分个体所构成的集合。

样本中所包含的个体数目。

0302 01总体与样本研究对象的全体个体所构成的集合。

随机抽样与非随机抽样随机抽样按照随机原则从总体中抽取样本的方法，保证每个个体被抽中的机会相等。

非随机抽样根据研究者的主观意愿或方便性选择样本的方法，可能导致选择偏倚。

变量与数据类型变量研究中观察或测量的特征或属性。

数据类型根据变量的性质可分为定量数据和定性数据。

定量数据包括连续型数据和离散型数据，定性数据包括分类数据和顺序数据。

统计量与参数统计量描述样本特征的量，如样本均数、样本标准差等。

参数描述总体特征的量，如总体均数、总体标准差等。

通常情况下参数是未知的，需要通过样本统计量进行估计。

03描述性统计方法频数分布表直方图应用场景频数分布表与直方图用于展示数据的分布情况，包括各组数据的频数、频率、累计频数和累计频率。

用矩形的面积表示各组频数，矩形的高度表示每一组的频数密度，宽度则表示组距。

适用于连续变量，可直观地展示数据的分布规律，如偏态、峰态等。

作为一名临床医师，有时为了完成一些小科研，或晋升职称，都必须撰写医学论文。

大多数人会碰到一个难题，医学论文的数据都必须进行统计学处理，上大学时学过的《医学统计学》早已忘得差不多了，重新翻开统计学书本，花上十天半个月的时间，还是看得不知所云。

《医学统计学傻瓜教程》有别于其他任何的统计学教程，其特点是略去一些高深难懂的统计学原理及计算公式，直奔解决实际问题的方法。

本教程的学习时间约需要2～3小时，但你必须曾经学过《医学统计学》，不管学得好或学得差，或是否已忘记，只要有一点印象即可，同时还需要下载一个简明统计学处理软件《临床医师统计学助手V3.0》，因为作数据统计学处理时最令人头痛的问题是烦琐的计算，则由预存在本软件内的计算公式来完成。

这是一个全“傻瓜化”的教程，由4个实例组成，只要认真看完这4个实例，将实际中碰到的问题对号入座，就足以解决绝大多数问题了。

接下来我们开始轻松愉快的学习过程。

一、均数与标准差【例1】本组105 例，男55例，女50例；平均年龄：62.3±6.1岁，所有入选病例均符合1999年WHO高血压诊断标准。

举这个例子是为了说明“均数”与“标准差”的概念。

我实在不愿意多花时间阐述一些概念性的东西，但是由于“标准差”实在太重要了。

【例1】中的数据“62.3±6.1”，“62.3”就是年龄的均数，均数的概念大家都懂，那么后面的“6.1”是什么呢？它就是标准差。

有人可能会问，表达一组人的平均年龄，用均数就够了，为什么还要加一个标准差呢？先看下面的一个例子：有两组人，第1组身高（cm）：98、99、100、101、102；第2组身高（cm）：80、90、100、110、120，这两组人虽然身高的均数都是100cm，但是，仔细观察，第1组的身高很接近，第2组的身高差别很大，故仅仅用一个平均数表达一组数据的特征是不完整的，还需要用另一个指标来表达其参差不齐的程度，这就是标准差。