弹塑性力学历年考题(杨整理)

弹塑性理论考试题及答案一、单项选择题（每题2分，共10分）1. 弹塑性理论中，材料的屈服准则通常用以下哪个参数表示？A. 应力B. 应变C. 弹性模量D. 屈服应力答案：D2. 弹塑性材料在循环加载下，其行为主要受哪个参数的影响？A. 最大应力B. 最大应变C. 应力幅值D. 应变幅值答案：C3. 根据弹塑性理论，材料的硬化指数n通常用来描述什么？A. 材料的弹性B. 材料的塑性C. 材料的断裂特性D. 材料的疲劳特性答案：B4. 在弹塑性理论中，哪个参数用来描述材料在塑性变形后能否恢复原状？A. 弹性模量B. 屈服应力C. 塑性应变D. 弹性应变答案：D5. 弹塑性材料在受到拉伸应力作用时，其应力-应变曲线通常呈现哪种形状？A. 线性B. 非线性C. 抛物线D. 指数曲线答案：B二、多项选择题（每题3分，共15分）6. 弹塑性理论中，材料的屈服准则可以由以下哪些因素确定？A. 应力状态B. 应变状态C. 温度D. 材料的微观结构答案：A|B|C|D7. 弹塑性材料在循环加载下，其疲劳寿命主要受哪些因素的影响？A. 应力幅值B. 材料的屈服应力C. 循环加载频率D. 材料的微观缺陷答案：A|B|C|D8. 在弹塑性理论中，材料的硬化行为可以通过以下哪些方式来描述？A. 硬化指数B. 硬化模量C. 应力-应变曲线D. 屈服应力答案：A|B|C9. 弹塑性材料在受到压缩应力作用时，其应力-应变曲线通常呈现以下哪些特点？A. 初始阶段为弹性B. 达到屈服点后进入塑性变形C. 塑性变形后材料体积不变D. 卸载后材料能够完全恢复原状答案：A|B|C10. 弹塑性理论中，材料的断裂特性可以通过以下哪些参数来描述？A. 断裂韧性B. 应力集中系数C. 材料的硬度D. 材料的塑性应变答案：A|B|C|D三、简答题（每题5分，共20分）11. 简述弹塑性理论中材料的屈服现象。

答：在弹塑性理论中，材料的屈服现象是指材料在受到一定的应力作用后，从弹性变形转变为塑性变形的过程。

塑性力学考试题及答案一、选择题（每题2分，共20分）1. 塑性变形与弹性变形的主要区别是（）。

A. 塑性变形是可逆的B. 弹性变形是可逆的C. 塑性变形是不可逆的D. 弹性变形是不可逆的2. 材料在塑性变形过程中，其应力-应变曲线上的哪一点标志着材料的屈服点？A. 最大应力点B. 最大应变点C. 应力-应变曲线上的转折点D. 应力-应变曲线的起始点3. 下列哪项不是塑性变形的特征？A. 材料形状的改变B. 材料体积的不变C. 材料内部结构的不可逆变化D. 材料的弹性恢复4. 塑性变形的三个基本假设中，不包括以下哪一项？A. 材料是连续的B. 材料是各向同性的C. 材料是不可压缩的D. 材料是完全弹性的5. 塑性变形的流动法则通常采用哪种形式来描述？A. 线性形式B. 非线性形式C. 指数形式D. 对数形式二、简答题（每题10分，共30分）6. 简述塑性变形的三个基本假设及其物理意义。

7. 解释什么是塑性屈服准则，并举例说明常用的屈服准则。

8. 描述塑性变形过程中的加载和卸载路径，并解释它们的区别。

三、计算题（每题25分，共50分）9. 给定一个材料的应力-应变曲线，如果材料在达到屈服点后继续加载，求出在某一特定应变下的材料应力。

10. 假设一个材料在单轴拉伸条件下发生塑性变形，已知材料的屈服应力和弹性模量，求出在塑性变形阶段的应变率。

答案一、选择题1. 答案：C2. 答案：C3. 答案：D4. 答案：D5. 答案：B二、简答题6. 塑性变形的三个基本假设包括：- 材料是连续的：假设材料没有空隙和裂缝，是连续的均匀介质。

- 材料是各向同性的：假设材料在所有方向上具有相同的物理性质。

- 材料是不可压缩的：假设在塑性变形过程中材料的体积保持不变。

7. 塑性屈服准则是判断材料是否开始发生塑性变形的条件。

常用的屈服准则包括：- Von Mises准则：适用于各向同性材料，当材料的等效应力达到某一临界值时，材料开始发生塑性变形。

---○---○------○---○---………… 评卷密封线 ……………… 密封线内不要答题，密封线外不准填写考生信息，违者考试成绩按0分处理 ……………… 评卷密封线 …………中南大学考试试卷（参考答案）2010~2011 学年 二 学期 弹塑性力学 课程 时间110分钟32 学时， 2学分，闭卷，总分100分，占总评成绩 90 %一、名词解释题（每小题3分，共15分）1、应力强度因子：2、弹塑性共存：3、应力集中：4、弹塑性体5、二、填空题 (每小题2分，共24分)1、主应力平面上的切应力等于零；主切应力平面上的正应力 不一定等于零。

2、全量应变是 某时刻变形之后的应变量 ； 应变增量是 变形某时刻的应变微分量 。

3、在应力分量表达式σij 中，下标i 表示 应力分量所在平面的外法线方向 ， 下标j 表示 应力分量本身的作用方向 。

4、已知主应变ε1>ε2>ε3，则最大剪应变为：γmax = ε1-ε3 。

5、表征变形体内各应力分量之间相互关系的是 应力平衡微分 方程，表征各应变分量之间相互关系的是 应变连续/协调 方程。

6、在滑开型裂纹扩展模式中，应力的作用方向与裂纹扩展方向 平行 ，裂纹面与应力作用方向 平行 。

7、如图所示，受单向均匀拉伸载荷的平板构件，其上的中心穿透小孔边缘的a 、b 及远离小孔的c 、d 点，随着外载荷增加，最先进入塑性变形状态的是 a 点，受压应力的是 b 点。

8、如图所示为变形体内某点处单元体的受力状态，已知σ=σs （屈服应力），用Tresca 屈服准则判别，该点处于 塑性变形 状态；用Mises 屈服准则判别，该点处于 弹性变形 状态。

9、圆柱体在Z 向受压缩，产生均匀塑性变形，则其塑性应变之比为：=px px px εεε::。

10、 11、 12、题二（8）图题二（7）图1.5σσx---○---○------○---○---………… 评卷密封线 ……………… 密封线内不要答题，密封线外不准填写考生信息，违者考试成绩按0分处理 ……………… 评卷密封线 …………三、简析题（共25分）1、试根据弹性力学原理，分析受强内压力作用的厚壁筒的结构设计方法。

考试科目：弹塑性力学试题班号 研 班 姓名 成绩一、 概念题（1） 最小势能原理等价于弹性力学平衡微分方程和静力边界条件，用最小势能原理求解弹性力学近似解时，仅要求位移函数满足已知位移边界条件。

（2） 最小余能原理等价于 应变协调 方程和 位移 边界条件，用最小余能原理求解弹性力学近似解时，所设的应力分量应预先满足平衡微分方程 和静力边界条件。

（3） 弹性力学问题有位移法和应力法两种基本解法，前者以位移为基本未知量，后者以 应力为基本未知量。

二、已知轴对称的平面应变问题，应力和位移分量的一般解为：利用上述解答求厚壁圆筒外面套以绝对刚性的外管，厚壁圆筒承受内压p 作用，试求该问题的应力和位移分量的解。

解：边界条件为：a r =时：p r -=σ；0=θτrb r =时：0=r u ；0=θu 。

将上述边界条件代入公式得： 解上述方程组得：则该问题的应力和位移分量的解分别为： 三、已知弹性半平面的o点受集中力p利用上述解答求在弹性半平面上作用着n 这些力到所设原点的距离分别为i y ,y解：由题设条件知，第i 个力i p 在点（x ，y ）处产生的应力将为： 故由叠加原理，n 个集中力构成的力系在点（x ，y ）处产生的应力为：四、一端固定，另一端弹性支承的梁，其跨度为l ，抗弯刚度EI 为常数，弹簧系数为k ,承受分布荷载)(x q 作用。

试用最小势能原理导出该梁以挠度形式表示的平衡微分方程和静力边界条件。

解：第一步：全梁总应变能为：dx dx w d EI wdv U l v 202221⎰⎰⎥⎦⎤⎢⎣⎡== 外力做功为：⎰=-=ll x kw qwdx T02|21总势能为：l x l lkw qwdx dx dx w d EI T U =⎰⎰+-⎥⎦⎤⎢⎣⎡=-=∏|2121202022 第二步：由最小势能原理可知：0=∏δ等价于平衡微分方程和静力边界条件。

l x l lw kw wdx q dx dx w d dx w d EI =⎰⎰+-⎪⎪⎭⎫⎝⎛⎥⎦⎤⎢⎣⎡=|022022δδδ （*） 其中=⎪⎪⎭⎫ ⎝⎛⎥⎦⎤⎢⎣⎡⎰dx dx w d dx w d EI l22022δdx dx dw dx d dx w d EI l ⎥⎦⎤⎢⎣⎡⎪⎭⎫ ⎝⎛⎥⎦⎤⎢⎣⎡⎰δ022 将其代入（*）式并整理可得：由于当0=x 时，0=dxdw ，022=dx w d ；所以平衡微分方程为：0)(2222=-⎥⎦⎤⎢⎣⎡⎪⎪⎭⎫ ⎝⎛x q dx w d EI dx d （0≤x ≤l ）y静力边界条件为：⎪⎪⎩⎪⎪⎨⎧=⎪⎪⎭⎫ ⎝⎛=⎪⎭⎪⎬⎫⎪⎩⎪⎨⎧⎥⎦⎤⎢⎣⎡⎪⎪⎭⎫ ⎝⎛-==002222l x lx dx w d dx w d EI dx d kw五、已知空间球对称问题的一般解为：B REA EB R EA E R BR A u T R R 332)1(21)1(221μμσμμσ++-=+--=+=其中R 是坐标变量，R u 是径向位移，R σb a q q ,q 时的解答。

2.9已知应力分量中0x y xy σστ===，求三个主应力123σσσ≥≥。

解 在0x y xy σστ===时容易求得三个应力不变量为1z J σ=，2222yz zx J τττ=+=，30J =特征方程变为32222()0z z σσστσσσσστ--=--=求出三个根，如记1τ=112312,0,2z z σστσσστ=+==-记123σσσ≥≥4.10有一长度为l 的简支梁，在x a =处受集中力P 作用，见题图4.6，试用瑞兹法和伽辽金法求梁中点的挠度。

题图4-6解一：用瑞兹法求解设满足梁端部位移边界条件0,0x l w ==的挠度函数为sinm mm xw B lπ=∑ （1） 梁的变形能U 及总势能∏为2224423001224llmmM EI d w EI U dx dx m BEI dx l π⎛⎫=== ⎪⎝⎭∑⎰⎰443sin 4m mm m EI m a m B P B l l ππ∏=-∑∑ 由0mB ∂∏=∂得 3442sin m m a Pl l B EI mππ=344sinsin 2mm a m xPl l l w EI mπππ=∑（2）以上级数的收敛性很好，取很少几项就能得到满意的近似解，如P 作用于中点（2a l =）时，跨中挠度为（只取一项）3342248.7x l Pl Pl w EI EIπ=== 这个解与材料力学的解（348Pl EI）相比，仅相差1.5%。

解二：用伽辽金法求解1.当对式（1）求二阶导数后知，它满足220,0x ld wdx==，亦即满足支承处弯矩为零的静力边界条件，因此，可采用伽辽金求解。

将式（1）代入伽辽金方程，注意到qdx P =，且作用在x a =处，可得420sin sin 0lm m m x m a EIB dx P l l l πππ⎡⎤⎛⎫⎛⎫-=⎢⎥ ⎪ ⎪⎝⎭⎝⎭⎢⎥⎣⎦⎰ 3442sinm m aPl l B EI mππ= 求出的挠度表达式与（2）一致。

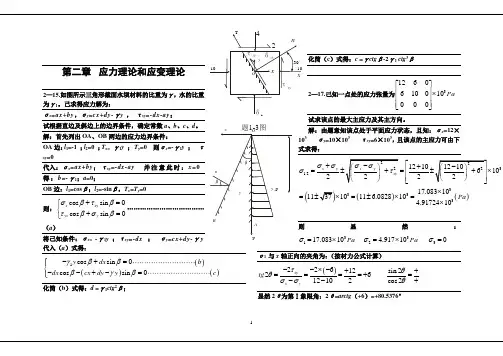
第二章 应力理论和应变理论2—15.如图所示三角形截面水坝材料的比重为γ，水的比重为γ1。

己求得应力解为：σx =ax+by ，σy =cx+dy-γy ， τxy =-dx-ay ；试根据直边及斜边上的边界条件，确定常数a 、b 、c 、d 。

解：首先列出OA 、OB 两边的应力边界条件：OA 边：l 1=-1 ；l 2=0 ；T x = γ1y ； T y =0 则σx =-γ1y ； τxy =0代入：σx =ax+by ；τxy =-dx-ay 并注意此时：x =0 得：b=-γ1；a =0；OB 边：l 1=cos β；l 2=-sin β，T x =T y =0则：cos sin 0cos sin 0x xy yxy σβτβτβσβ+=⎧⎨+=⎩………………………………（a ）将己知条件：σx= -γ1y ；τxy =-dx ； σy =cx+dy-γy 代入（a ）式得：()()()1cos sin 0cos sin 0y dx b dx cx dy y c γβββγβ-+=⎧⎪⎨--+-=⎪⎩化简（b ）式得：d =γ1ctg 2β；化简（c ）式得：c =γctg β-2γ1 ctg 3β2—17.己知一点处的应力张量为31260610010000Pa ⎡⎤⎢⎥⨯⎢⎥⎢⎥⎣⎦试求该点的最大主应力及其主方向。

解：由题意知该点处于平面应力状态，且知：σx =12×103 σy =10×103 τxy =6×103，且该点的主应力可由下式求得：(()()31.233331210102217.0831******* 6.082810 4.9172410x yPa σσσ⎡++⎢=±=⨯⎢⎣⨯=⨯=±⨯=⨯则显然：3312317.08310 4.917100Pa Pa σσσ=⨯=⨯=σ1 与x 轴正向的夹角为：（按材力公式计算）()22612sin 22612102cos 2xyx ytg τθθσσθ--⨯-++====+=--+显然2θ为第Ⅰ象限角：2θ=arctg （+6）=+80.5376°题图1-3则：θ=+40.268840°16＇ 或（-139°44＇）2—19.己知应力分量为：σx =σy =σz =τxy =0，τzy =a ，τzx =b ，试计算出主应力σ1、σ2、σ3并求出σ2的主方向。

《应用弹塑性力学》考试试卷班级_____________ 姓名_____________ 学号______________一、简答题（每题5分，共20分）1试述弹塑性力学中四种常用的简化力学模型及其特点。

2分析特雷斯卡（Tresca ）和米泽斯（Mises ）屈服条件的异同点。

3 简单论述一下屈服曲面为什么一定是外凸的。

4试述逆解法和半逆解法的主要思想。

二、计算题（1~5题每题10分， 6~7题每题15分，共80分）1 如图1所示的等截面直杆，截面积为0A ，且b a >，在x a =处作用一个逐渐增加的力P 。

该杆材料为理想弹塑性，拉伸和压缩时性能相同，求左端反力N F 和力P 的关系。

F N图12 已知下列应力状态：5383038311ij MPa σ⎡⎤⎢⎥=⎢⎥⎢⎥⎣⎦，试求八面体单元的正应力0σ与剪应力0τ。

3 已知物体某点的应力分量，试求主应力及最大剪应力的值。

（单位MPa ）（1）x =10σ，y =10σ-，z =10σ，=0xy τ，=0yz τ，=10zx τ-；（2）x =10σ，y =20σ，z =30σ，=5xy τ-，=0yz τ，=0zx τ。

4 当123σσσ>>时，如令213132σσσσμσσ--=-，试证明0max ττ=且该值在0.816~0.943之间。

5已知平面应变状态1231231230x y xy z xz yz A A x A yB B x B yC C x C yεεγεγγ=++=++=++===（1）校核上述应变状态是否满足应变协调方程；（2）若满足应变协调方程，试求位移u 和v 的表达式；（3）已知边界条件 0x y ==，0u =，0v =；x l =，0y =，0v =确定上述位移表达式中的待定常数。

6 物体中某点的应力状态为100000200000300-⎡⎤⎢⎥-⎢⎥⎢⎥-⎣⎦MPa ，该物体在单向拉伸时屈服极限为190MPa s σ=，试分别用特雷斯卡（Tresca ）和米泽斯（Mises ）屈服条件来判断该点是处于弹性状态还是塑性状态。

弹塑性力学考试————————————————————————————————作者：————————————————————————————————日期：二、填空题：（每空2分，共8分）1、在表征确定一点应力状态时，只需该点应力状态的-------个独立的应力分量，它们分别是-------。

（参照oxyz直角坐标系）。

2、在弹塑性力学应力理论中，联系应力分量与体力分量间关系的表达式叫---------方程，它的缩写式为-------。

三、选择题（每小题有四个答案，请选择一个正确的结果。

每小题4分，共16分。

）1、试根据由脆性材料制成的封闭圆柱形薄壁容器，受均匀内压作用，当压力过大时，容器出现破裂。

裂纹展布的方向是：_________。

A、沿圆柱纵向（轴向）B、沿圆柱横向（环向）C、与纵向呈45°角D、与纵向呈30°角2、金属薄板受单轴向拉伸，板中有一穿透形小圆孔。

该板危险点的最大拉应力是无孔板最大拉应力__________倍。

A、2B、3C、4D、53、若物体中某一点之位移u、v、w均为零（u、v、w分别为物体内一点，沿x、y、z直角坐标系三轴线方向上的位移分量。

）则在该点处的应变_________。

A、一定不为零B、一定为零C、可能为零D、不能确定4、以下________表示一个二阶张量。

A、B、C、D、四、试根据下标记号法和求和约定展开下列各式：（共8分）1、；（i ，j = 1，2，3 ）；2、；五、计算题（共计64分。

）1、试说明下列应变状态是否可能存在：；（）上式中c为已知常数，且。

2、已知一受力物体中某点的应力状态为：式中a为已知常数，且a＞0，试将该应力张量分解为球应力张量与偏应力张量之和。

为平均应力。

并说明这样分解的物理意义。

3、一很长的（沿z轴方向）直角六面体，上表面受均布压q作用，放置在绝对刚性和光滑的基础上，如图所示。

若选取＝ay2做应力函数。

试求该物体的应力解、应变解和位移解。

二、填空题：（每空2分，共8分）1、在表征确定一点应力状态时，只需该点应力状态的-------个独立的应力分量，它们分别是-------。

（参照oxyz直角坐标系）。

2、在弹塑性力学应力理论中，联系应力分量与体力分量间关系的表达式叫---------方程，它的缩写式为-------。

三、选择题（每小题有四个答案，请选择一个正确的结果。

每小题4分，共16分。

）1、试根据由脆性材料制成的封闭圆柱形薄壁容器，受均匀内压作用，当压力过大时，容器出现破裂。

裂纹展布的方向是：_________。

A、沿圆柱纵向（轴向）B、沿圆柱横向（环向）C、与纵向呈45°角D、与纵向呈30°角2、金属薄板受单轴向拉伸，板中有一穿透形小圆孔。

该板危险点的最大拉应力是无孔板最大拉应力__________倍。

A、2B、3C、4D、53、若物体中某一点之位移u、v、w均为零（u、v、w分别为物体内一点，沿x、y、z直角坐标系三轴线方向上的位移分量。

）则在该点处的应变_________。

A、一定不为零B、一定为零C、可能为零D、不能确定4、以下________表示一个二阶张量。

A、B、C、D、四、试根据下标记号法和求和约定展开下列各式：（共8分）1、；（i ，j = 1，2，3 ）；2、；五、计算题（共计64分。

）1、试说明下列应变状态是否可能存在：；（）上式中c为已知常数，且。

2、已知一受力物体中某点的应力状态为：式中a为已知常数，且a＞0，试将该应力张量分解为球应力张量与偏应力张量之和。

为平均应力。

并说明这样分解的物理意义。

3、一很长的（沿z轴方向）直角六面体，上表面受均布压q作用，放置在绝对刚性和光滑的基础上，如图所示。

若选取＝ay2做应力函数。

试求该物体的应力解、应变解和位移解。

（提示：①基础绝对刚性，则在x＝0处，u＝0 ；②由于受力和变形的对称性，在y＝0处，v＝0 。

）题五、3图4、已知一半径为R＝50mm，厚度为t＝3mm的薄壁圆管，承受轴向拉伸和扭转的联合作用。

⼯程弹塑性⼒学题库及答案第⼀章弹塑性⼒学基础1.1什么是偏应⼒状态？什么是静⽔压⼒状态？举例说明？解：静⽔压⼒状态时指微六⾯体的每个⾯只有正应⼒作⽤，偏应⼒状态是从应⼒状态中扣除静⽔压⼒后剩下的部分。

1.2对照应⼒张量与偏应⼒张量，试问：两者之间的关系？两者主⽅向之间的关系？解：两者主⽅向相同。

1.3 简述应⼒和应变Lode参数定义及物理意义：解：µσ的定义、物理意义：；1) 表征S ij的形式；2) µσ相等，应⼒莫尔圆相似，S ij形式相同；3) 由µσ可确定S1：S2：S3。

1.4设某点应⼒张量的分量值已知，求作⽤在过此点平⾯上的应⼒⽮量，并求该应⼒⽮量的法向分量。

解：该平⾯的法线⽅向的⽅向余弦为⽽应⼒⽮量的三个分量满⾜关系⽽法向分量满⾜关系最后结果为：1.5利⽤上题结果求应⼒分量为时，过平⾯处的应⼒⽮量，及该⽮量的法向分量及切向分量。

解：求出后，可求出及，再利⽤关系可求得。

最终的结果为，1.6 已知应⼒分量为，其特征⽅程为三次多项式，求。

如设法作变换，把该⽅程变为形式，求以及与的关系。

解：求主⽅向的应⼒特征⽅程为式中：是三个应⼒不变量，并有公式代⼊已知量得为了使⽅程变为形式，可令代⼊，正好项被抵消，并可得关系代⼊数据得，，1.7已知应⼒分量中，求三个主应⼒。

解：在时容易求得三个应⼒不变量为，，特征⽅程变为求出三个根，如记，则三个主应⼒为记1.8已知应⼒分量，是材料的屈服极限，求及主应⼒。

解：先求平均应⼒，再求应⼒偏张量，，，，，。

由此求得：然后求得：，，解出然后按⼤⼩次序排列得到，，1.9 已知应⼒分量中，求三个主应⼒，以及每个主应⼒所对应的⽅向余弦。

解：特征⽅程为记，则其解为，，。

对应于的⽅向余弦，，应满⾜下列关系（a）（b）（c）由（a）,(b)式，得，，代⼊（c）式，得，由此求得对，，代⼊得对，，代⼊得对，，代⼊得1.10当时，证明成⽴。

解：由，移项之得证得第五章简单应⼒状态的弹塑性问题5.1简述Bauschinger效应：解：拉伸塑性变形后使压缩屈服极限降低的现象5.2在拉杆中，如果和为试件的原始截⾯积和原长，⽽和为拉伸后的截⾯积和长度。

第二章 应力理论和应变理论2— 15.如 所示三角形截面水 材料的比重 γ，水的比重 γ 1。

己求得 力解 ：σ x = ax+by ， σy =cx+dy- γy ， τxy =-dx-ay ；根据直 及斜 上的 界条件，确定常数 a 、b 、c 、 d 。

解：首先列出OA 、 OB 两 的 力 界条件：OA ：l 1=-1 ；l 2=0 ；T x= γ1 y ； T y =0σx =-γ1y ； τxy =0代入： σx =ax+by ； τxy =-dx-ay 并 注 意 此 ： x =0得 ： b=- γ1； a=0；OB ： l 1=cos β ； l 2=-sin β， T x =T y =0：x cosxy sin0 yx cosy sin⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯（ a ）将己知条件： σ x=1xy=-dxyγ y-γ y ； τ； σ =cx+dy-代入（ a ）式得：1 y cos dx sin0L L L L L L L L L bdx coscxdyy sin L L L L L L L L L化 （ b ）式得： d = γ12β；ctgT4n2τ 30° δ 30°30°化 （ c ）式得： c =γctg β -2γ 13y10x10Ox12 6τxy103 Pa2— 17.己知一点 的 力 量6 10 00 0δ y求 点的最大主 力及其主方向。

x题1-3 图解：由 意知 点 于平面 力状 ，且知：σx =12×O103σ y =10× 103 τ xy =6× 103，且 点的主 力可由下式求得：β212 101221.2xyxy21023n 22xy22610βγ 1y113710311 6.0828 10317.083 10 3 Paγ34.91724 10BA然：y117.083 10 3Pa2 4.917 10 3Pa30σ 1 与 x 正向的 角 ： （按材力公式 算）c2 xy2 6 12 sin 2tg 2121026xycos2然 2θ 第Ⅰ象限角： 2θ=arctg （ +6） =+80.5376 °则：θ=+40.2688 B 40° 16＇或（-139° 44＇）2— 19.己知应力分量为：σx=σy=σz=τxy=0，τzy=a，τzx=b，试计算出主应力σ1、σ2、σ3 并求出σ2 的主方向。

弹塑性力学题库与答案第二章应力理论和应变理论2―3．试求图示单元体斜截面上的σ30°和τ30°（应力单位为MPa）并说明使用材料力学求斜截面应力为公式应用于弹性力学的应力计算时，其符号及正负值应作何修正。

…解：在右图示单元体上建立xoy坐标，则知σx -10 σy -4 τxy -2（以上应力符号均按材力的规定）代入材力有关公式得：代入弹性力学的有关公式得：己知σx -10 σy -4 τxy +2 由以上计算知，材力与弹力在计算某一斜截面上的应力时，所使用的公式是不同的，所得结果剪应力的正负值不同，但都反映了同一客观实事。

2―6. 悬挂的等直杆在自重W作用下（如图所示）。

材料比重为γ弹性模量为 E，横截面面积为A。

试求离固定端z处一点C的应变εz与杆的总伸长量Δl。

解：据题意选点如图所示坐标系xoz，在距下端（原点）为z处的c点取一截面考虑下半段杆的平衡得：c截面的内力：Nz γ??A??z ；c截面上的应力：；所以离下端为z处的任意一点c的线应变εz为：；则距下端（原点）为z的一段杆件在自重作用下，其伸长量为：；显然该杆件的总的伸长量为（也即下端面的位移）：；（W γAl）2―9.己知物体内一点的应力张量为：σij应力单位为kg／cm2 。

试确定外法线为ni｛，，｝（也即三个方向余弦都相等）的微分斜截面上的总应力、正应力σn及剪应力τn 。

解：首先求出该斜截面上全应力在x、y、z三个方向的三个分量：n’ nx ny nzPx n’Py n’Pz n’所以知，该斜截面上的全应力及正应力σn、剪应力τn均为零，也即：Pn σn τn 02―15.如图所示三角形截面水坝材料的比重为γ，水的比重为γ1。

己求得应力解为：σx ax+by，σy cx+dy-γy ，τxy -dx-ay；试根据直边及斜边上的边界条件，确定常数a、b、c、d。

解：首先列出OA、OB两边的应力边界条件：OA边：l1 -1 ；l2 0 ；Tx γ1y ； Ty 0 则σx -γ1y ；τxy 0代入：σx ax+by；τxy -dx-ay 并注意此时：x 0得：b -γ1；a 0；OB边：l1 cosβ；l2 -sinβ，Tx Ty 0则：………………………………（a）将己知条件：σx -γ1y ；τxy -dx ；σy cx+dy-γy代入（a）式得：化简（b）式得：d γ1ctg2β；化简（c）式得：c γctgβ-2γ 1 ctg3β2―17.己知一点处的应力张量为试求该点的最大主应力及其主方向。