五点法画正弦交流电波形图

Science &Technology Vision科技视界0引言正弦交流电是电工基础课程中的一个重要的章节，涉及三角函数、复数等大量数学知识。

技工院校的学生大多数学基础薄弱，而电工老师不可能拿出大量时间讲授相关数学知识，导致学生无法真正掌握其中原理。

作为电工相关专业的数学老师，有必要将数学的有关知识和原理渗透于正弦交流电的学习中，在数学和正弦交流电之间搭起一座桥梁。

这需要数学老师掌握相关的电工知识，科学系统地设计出一套行之有效的教学方案。

只要在三角函数和复数的教学中把握以下三条主线，就能为正弦交流电铺平道路。

本文浅析正弦交流电相关数学知识的讲解。

1在线段“旋转”中阐释两个“为什么”“为什么线圈切割磁感线形成的交流电可以用一个正弦型函数来表示？”“为什么正弦量可以用复数来表示？”很多学生被这两个问题困扰着。

要从本质上认识正弦交流电及掌握有关计算，就绕不开这两个核心问题。

从数学的角度来看，问题的本质都是研究线段“旋转”过程中在垂直方向或水平方向产生的投影值的变化规律。

1.1在“旋转”中阐释“为什么正弦量可以用复数来表示?”正弦量用复数表示的推理过程与正弦函数图像的形成过程是相通的，运用相似的“旋转”原理。

如图1所示，在动态演示中，设有正弦电压u=U m sin （ω+φ），其波形如图1b 所示，在左边直角坐标系中取长度为U m有向线段，初始位置与x 轴正方向的夹角为φ，并以角频率ω作逆时针旋转。

根据三角函数计算，同时结合动态图可见，旋转有向线段任一时刻t 在纵轴上的投影值刚好对应正弦量在该时刻的瞬时值u （t ）=U m sin（ωt+φ）。

因为旋转的有向线段里面包含了正弦量的三个特征量，长度是正弦量的振幅U m ，初始位置是正弦量的初相φ，而旋转的角频率是ω，可见一个旋转的有向线段可以表示一个正弦量。

图1如果有两个正弦量，就可以在坐标里画出两个有向线段，如图2所示。

由于在同一正弦稳态性电路中，正弦量频率都是相同的，所以同频率的旋转有向线段的相对位置是不变的，可以把频率隐含起来，让旋转的有向线段固定在初始位置，如图3所示。

文化理论课教案7.5.1-10-j-01：【组织教学】1. 起立，师生互相问好2. 坐下，清点人数，指出和纠正存在问题【导入新课】我们已经学习了直流电和直流电路的有关计算，现在我们来学习交流电及交流电路的有关计算。

什么是交流电，它与直流电有什么不同呢？学了本课，我们回答这些问题。

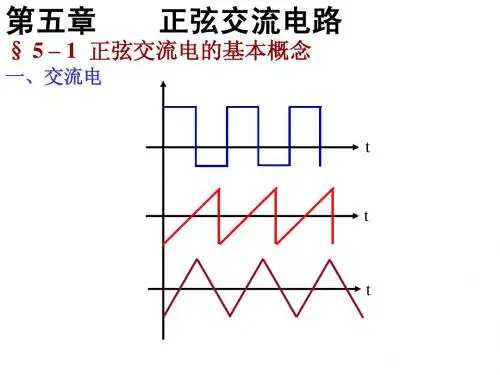
【讲授新课】第五章 单相交流电路 §5－1 交流电的基本概念一、什么交流电恒稳直流电：大小和方向不随时间变化的电流、电压、电动势的总称，常简称为直流电。

脉动直流电：大小随时间有些变化而方向不变的电流、电压、电动势的总称。

交流电：大小和方向都随时间作周期性变化的电流、电压、电动势的总称。

正弦交流电：按正弦函数规律变化的交流电。

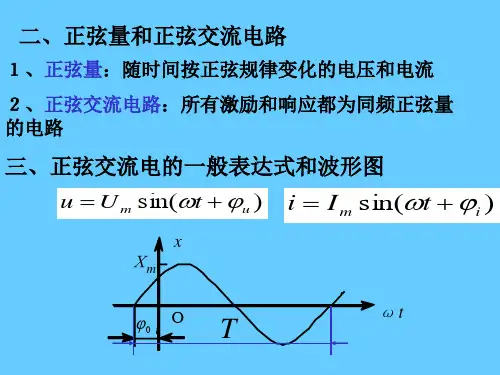
交流电流、电压、电动势的其数学表达式分别为：0sin()sin()sin()m i m u m i I t u E t e E t ωϕωϕωϕ=+=+=+ 通过交流电的电路叫交流电路，通过正弦交流电的电路正弦交流电路。

电路中的电源如果只有单个交流电动势，这样的电路叫单相交流电路；电路中的电源如果有三个交流电动势，这样的电路叫三相交流电路。

二、正弦交流电的产生正弦交流电是正弦交流发电机产生的，图5—1是正弦交流发电机原理图。

正弦交流发电机的主要部分是线圈和磁极线圈：多用铜线绕成矩形，有许多匝，匝数越多，产生的感应电动势越大。

磁极：至少一对，多的达40对以上。

磁极对数越多的发电机，产生的交流电的变化速度越快。

图示发电机的磁极对数为一对。

磁极特制成：①磁极中线面的磁感应强度最强，为m B ；电枢表面上其他位置的磁感应强度按正弦函数规律变化：若线圈平面与磁极中性面的夹角为α，则线圈导体所处的磁感应强度为sin m B B α=。

②磁感应强度方向与导体的运动方向垂直，即v B ⊥。

设线圈的有效长度为l ，线圈平面以角速度为ω逆时针方向旋转，与磁极中性面夹角为α，从a 指向d 的电动电动势为正，从d 指向a 的电动电动势为负，则线圈产生的感应电动势的大小为：sin()sin sin90sin sin m m m e Blv v B B l v B lv E ααα==== ，式中，m m E B lv =，表示交流电动势的最大值。

【中职教案】 1.2 正弦型函数（二）【教学目标】知识目标：了解正弦型函数与正弦函数的图像之间的关系，会利用“五点法”作出正弦型函数的图像． 能力目标：通过正弦型函数与正弦函数的图像之间的关系，学生数形结合的能力得到强化．【教学重点】利用“五点法”作出正弦型函数的图像．【教学难点】正弦型函数与正弦函数的图像之间的关系．【教学设计】正弦型函数的图像叫做正弦型曲线．作图的基本方法是“描点法”.例2是由作正弦曲线出发，每次增加一个系数，利用“描点法”作出各函数的图像．列表的过程中蕴含着变量替换的思想．将这四条曲线放到同一个坐标系中，可以看到它们之间的相互关联，从而，推广得到结论。

这种变换的介绍，对提高学生的数学思维能力和培养数形结合的习惯是大有帮助的．熟练之后，如果要求做出一个周期内的正弦曲线，可以直接描出五个点： (,0)ϕω-，(,)4TA ϕω-+，(,0)2T ϕω-+，3(,)4T A ϕω-+-，(,0)T ϕω-+．用光滑的曲线连接得到曲线．例3的作图就采用了这样的方法．【教学备品】教学课件．【课时安排】2课时．(90分钟)【教学过程】*巩固知识 典型例题例2 利用“五点法”作出下列各函数一个周期内的图像．（1）sin y x =；（2）sin 2y x =；（3）πsin(2)4y x =+；（4）π2sin(2)4y x =+． 解 （1）函数sin y x =的周期为2πT =．列表x 0 π2π3π22π x sin1-1以表中每组对应的x ,y 值为坐标，描出点),(y x ，用光滑的曲线顺次联结各点,得到函数sin y x =在一个周期内的图像（如图1－2）．图1－2（2）函数sin 2y x =的周期为πT =．列表 x0 π4 π23π4 π 2x 0 π2π3π22π sin 2y x =1－1以表中每组对应的x ,y 值为坐标，描出点),(y x ，用光滑的曲线顺次联结各点,得到函数sin 2y x =在一个周期内的图像（如图1－3）．图1－3（3）函数πsin(2)4y x =+的周期为πT =．列表xπ8- π8 3π8 5π87π8 π24x +0 π2π3π22ππsin(2)4y x =+1－10 以表中每组对应的x ,y 值为坐标，描出点),(y x ，用光滑的曲线顺次联结各点,得到函数πsin(2)4y x =+在一个周期内的图像（如图1－4）．图1－4（4）函数π2sin(2)4y x =+的周期为πT =．列表xπ8- π8 3π8 5π87π8π24x +0 π2π3π22πsin 2y x = 0 1 0 －1 0 π2sin(2)4y x =+2－2以表中每组对应的x ，y 值为坐标，描出点),(y x ，用光滑的曲线顺次联结各点,得到函数πsin(2)4y x =+在一个周期内的图像（如图1－5）．图1－5将例2中的四条曲线，放到同一个坐标系中（如图1－6），可以看到将正弦曲线y = sin x ([02π])x ∈，上所有点的横坐标缩短到原来的12倍（纵坐标不变），可以得到正弦型曲线y = sin2x ；将正弦型曲线y = sin2x 向左平移π8个单位，可以得到正弦型曲线πsin(2)4y x =+；将正弦型曲线πsin(2)4y x =+的所有点的纵坐标伸长到原来的2倍，可以得到正弦型曲线π2sin(2)4y x =+．图1－6*巩固知识 典型例题例3 利用“五点法”作出正弦型曲线3πsin(3)26y x =-，并指出曲线经过怎样的步骤可以由正弦曲线得到．解 正弦型函数3πsin(3)26y x =-的周期为2π3T =，3ω=，π6ϕ=-．故五个关键点的坐标为π(0)18，，2π3()92，，7π(0)18，，5π3()92-，，13π(0)18，． 用光滑的曲线顺次联结各点,得到函数3πsin(3)26y x =-在一个周期内的图像（如图1－8）．图1－8函数3πsin(3)26y x =-可以看作由下面的方法得到：首先将正弦曲线y =sin x 上的所有点的坐标缩短到原来的13倍（纵坐标不变）；然后把所得的曲线向右平行移动π18个单位；最后把所得曲线上的所有点的纵坐标伸长到原来的1.5倍（横坐标不变）．*运用知识 强化练习【教师教学后记】。