研究生课内实验-高级运筹学-第二次

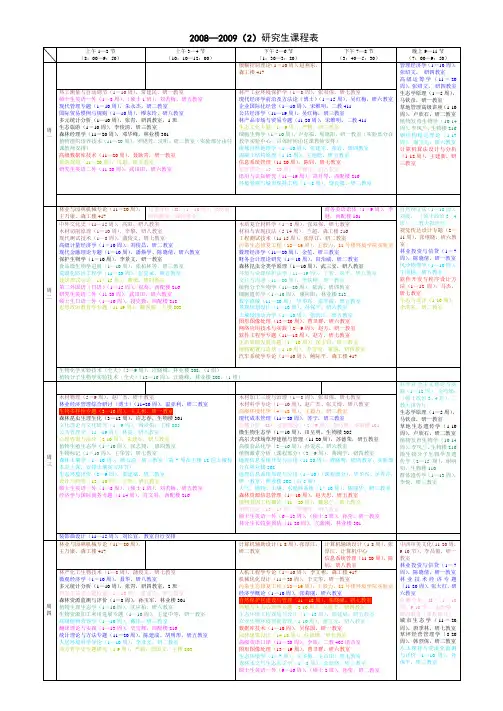
2008—2009（2）研究生课程表1、此课程表为经过核对调整后最终排定的课表，是进行教学检查的依据，原则上不再允许调课。

个别确需调整的请提前填写“北京林业大学研究生课程调课申请表”（可在“研究生院主页—下载中心—培养表格资料”处下载），提前一周办理调课手续。

并请同学们随时关注“研究生院主页—教学通知”专栏下的相关通知。

2、如果遇到节假日，课程调整按照学校党政办公室和教务处的通知执行，所耽搁的其他课程采取补课的形式（不能顺延）；如有特殊要求可关注“研究生院主页—教学通知”专栏下的通知。

3、涉及实验的课程，其实验部分由任课教师在上课时根据选课情况和具体实验条件等进行安排。

4、需要在计算机中心进行上机实验的课程，请任课教师提前与计算机中心取得联系，做好安排；否则，计算机中心不给安排上机实验。

并请同学们在实验前在计算机中心办好上机卡；否则，计算机中心不接纳上机，也无法完成实验部分课程，无法上机实验的同学也请不要选择相关课程。

5、以下部分课程的具体安排如下，请随时关注网上通知，可以与任课教室或开课学院联系。

（1）经济管理学院（62337226）《林业经济理论与政策专题》：刘俊昌，请国外专家协助讲此课，集中在第7至9周；《国外林业经济学专题》：温亚利，外请专家集中上课；《环境经济学》：高岚，请国外专家协助讲此课，集中授课；《国际运输与物流》：侯方淼，2月中旬至3月中旬集中授课。

（2）生物学院（62336013）《森林生物识别与鉴赏》：张志翔、李凯，2009.6.22~25（第19周）周一、二、四，生物楼315，实习时间为2009.7.1~8日，地点在杨家坪林场；《植物显微技术》：李凤兰，第13周周一至周五全天，生物楼216、211；《植物生理大实验》：郑彩霞等，第2~3周，周一至周日全天集中开课，林业楼201、204、218、220。

（3）园林学院（62338079）《野生园林植物资源调查采集》：潘会堂，暑假开始后两周内完成（5天），实习地点：百花山，此课仅限园林学院各学科的研究生选修。

1. 假设有一百万元可以投资到三支股票上，设随机变量iR 表示投资到股票i 上的一元钱每年能够带来的收益。

通过对历史数据分析，知期望收益1()0.09E R =，2()0.07E R =，3()0.06E R =，三支股票的协方差矩阵为0.200.030.040.030.200.050.040.050.15⎡⎤⎢⎥⎢⎥⎢⎥⎣⎦。

假设使用股票涨跌稳定性来评测风险，试构建优化模型，在保证期望年收益率不低于0.075的情况下，风险最小，同时表示为非线性优化的向量形式。

解：设123(,,)T X x x x =，其中123,,x x x 分别表示投资组合中123,,R R R 的所占的比例，有1231x x x ++= ……①保证期望收益率不低于0.075：112233()()()0.075x E R x E R x E R ++≥ ……②建立如下优化模型：222123121323min ()0.200.200.150.060.080.10f X x x x x x x x x x =+++++ ..s t 1231x x x ++=1230.090.070.060.075x x x ++≥123,,0x x x ≥记：0.200.030.040.030.200.050.040.050.15A ⎡⎤⎢⎥=⎢⎥⎢⎥⎣⎦表示成向量形式：min ()T f X X AX =..s t 1111T X ⎛⎫⎪= ⎪ ⎪⎝⎭0.090.070.0750.06T X ⎛⎫ ⎪≥ ⎪ ⎪⎝⎭123,,0x x x ≥2. 用伪算法语言描述“成功-失败”搜索方法。

解：1s ：初始化：0x , h,ε>02s ：x=0x ；1f =f(x) 3s ：2f =f(x+h)4s ： if 2f <1f go to 5s ;elsego to 6s ; end5s : x=x+h;2f =1f ;h=2h6s : if ||h ε<go to 7s ; else go to 8s ; end7s : x x *=8s : 4h h =-; go to 3s . □3. 请简述黄金分割法的基本思想，并尝试导出区间收缩比率φ≈0.618.基本思想：黄金分割法就是用不变的区间缩短率ϕ，来代替Fibonacci 法每次不同的缩短率，因而可以看成是Fibonacci 法的近似。

. 1实验报告实验课程名称运筹学实验工程名称大M法或两阶段法的上机实验年级专业学生学号00 学院实验时间：年月日实验容〔包括实验具体容、算法分析、源代码等等〕：1.书上P97页第6题：用大M 法和两阶段法求解以下线性规划问题。

ma* z=5；3213x x x ++ 约束条件：102x 4x x 321≥++，16.x 2x -x 321≤+A ：大M 法图1.1图1.2δ，得出目标函数的最优解*1=16，*2=0，由上面的结果可知，满足所求出的0≤j*3=0，s*4=16，R*5=0，s*=0，最优值是80。

当把M的值改为100000后，值还是一样的，这样就可以得出当M为100时，已经得出有效解。

B：两阶段法图1.3由图1.3可知，先进展线性规划的第一阶段，满足0≤j δ，且z 值为零，即说明存在一个可行解使得所有的人工变量都为零，此时*2=2.5，s*6=21，其余为0得出z=0。

接下来进展第二阶段，令z=5*1+*2+3*3-0s*4+0R*5+0s*6，和大M 的分析方法一样，最终将得到满足0≤j δ时到达最优解：当*1=16，*2=0，*3=0，s*4=6，R*5=0，s*6=0，最优值为80。

2.书上P97页第7题〔4〕大M 法和两阶段法求解以下线性规划问题 。

ma* z=；321x x 2x ++ 约束条件：，42x 2x 4x 321≥++，204x 2x 21≤+，162x 8x 4x 321≤++ A ：大M 法图2.1图2.2由上面的图 2.1可知，首先先输入数据即线性规划的系数如图 2.1所示令ma* z=321x x 2x ++-0s*4+0s*6+0s*7-MR*5；进展下一次迭代，以同样的方法一直下去，直到所求出的为止0≤j δ，就可以得出目标函数的最优解：*1=4，s*4=12，s*6=12，其余为0时，最优值为8。

当把M 的值改为100000后，值还是一样的，这样就可以得出当M 为100时，已经得出有效解。

一、课程概述课程名称：运筹学授课对象：清华大学经管学院管理科学与工程专业研究生授课时长：共16周，每周2学时教学目标：1. 理解运筹学的基本概念、原理和方法。

2. 掌握线性规划、整数规划、非线性规划等运筹学的基本模型和求解方法。

3. 培养学生运用运筹学解决实际问题的能力。

4. 提高学生的逻辑思维、分析问题和创新能力。

二、教学内容与安排第1-2周：运筹学的基本概念与数学基础1. 运筹学的基本概念、发展历程及应用领域。

2. 数学基础：线性代数、概率论与数理统计。

第3-4周：线性规划1. 线性规划的基本概念、数学模型与标准形式。

2. 线性规划的求解方法：单纯形法、对偶理论。

3. 线性规划的应用实例。

第5-6周：整数规划1. 整数规划的基本概念、数学模型与标准形式。

2. 整数规划的求解方法：分支定界法、割平面法。

3. 整数规划的应用实例。

第7-8周：非线性规划1. 非线性规划的基本概念、数学模型与标准形式。

2. 非线性规划的求解方法：梯度法、牛顿法、共轭梯度法。

3. 非线性规划的应用实例。

第9-10周：网络优化1. 网络优化的基本概念、数学模型与标准形式。

2. 网络优化的求解方法：最短路径法、最小生成树法、最大流问题。

3. 网络优化的应用实例。

第11-12周：动态规划1. 动态规划的基本概念、数学模型与标准形式。

2. 动态规划的求解方法：动态规划表、状态转移方程。

3. 动态规划的应用实例。

第13-14周：排队论1. 排队论的基本概念、数学模型与标准形式。

2. 排队论的求解方法：泊松过程、排队系统分析。

3. 排队论的应用实例。

第15-16周：案例分析1. 结合实际案例，分析运筹学在各个领域的应用。

2. 学生分组讨论，撰写案例分析报告。

三、教学方法与手段1. 讲授法：系统讲解运筹学的基本概念、原理和方法。

2. 案例分析法：通过实际案例，让学生理解运筹学的应用。

3. 讨论法：鼓励学生积极参与课堂讨论，提高学生的思考能力。

研究生数学教案：运筹学中的随机模型与优化算法1. 引言1.1 概述本文旨在探讨研究生数学教案中的运筹学内容，重点介绍随机模型与优化算法的应用。

运筹学作为一门基于数学方法和模型构建解决实际问题的学科，具有广泛的应用领域和重要性。

在现代社会中，随机性因素经常出现，并对决策和规划产生重要影响。

同时，为了提高决策的质量并优化实际问题的解决方案，各种优化算法也得到了广泛研究和应用。

1.2 文章结构本文共分为五个部分：引言、运筹学与数学教案、随机模型与应用、优化算法及其应用以及结论与展望。

在引言部分，我们将简要介绍本文的概述、文章结构以及目的。

1.3 目的本文旨在通过对研究生数学教案中运筹学相关内容的深入探讨，全面了解随机模型与优化算法在运筹学中的重要性及其具体应用。

通过详细介绍相关概念和原理，并借助实际案例分析和讨论，旨在帮助研究生更好地理解和应用这些数学方法，提高他们在运筹学领域的能力和素质。

通过系统的知识框架，本文还将对优化算法在随机模型中的应用研究进展以及现有成果进行总结，并探讨未来可能的研究方向。

希望本文能够为相关领域的研究工作者提供一定的参考和启示，进一步推动运筹学在实际问题中的应用以及优化算法的发展。

2. 运筹学与数学教案2.1 运筹学概述运筹学是一门综合应用数学和计算机科学的学科领域，旨在研究在各种实际问题中如何做出最佳决策。

它结合了数学模型、统计分析和优化方法等理论工具，以解决管理、工程、制造等领域中的实际问题。

2.2 数学教案介绍数学教案是指为教师准备和组织课堂教学所使用的材料和参考资料。

在研究生数学教育中，编写适合培养研究生创新思维和解决实际问题能力的数学教案尤为重要。

这些教案不仅可以引导研究生深入理解运筹学的基本概念和方法，还可以提供实际案例和应用场景，促进他们将所学内容与实际情境相结合。

2.3 研究生运筹学课程重要性研究生运筹学课程对于培养研究生的分析思考能力、数据建模能力以及问题解决能力至关重要。

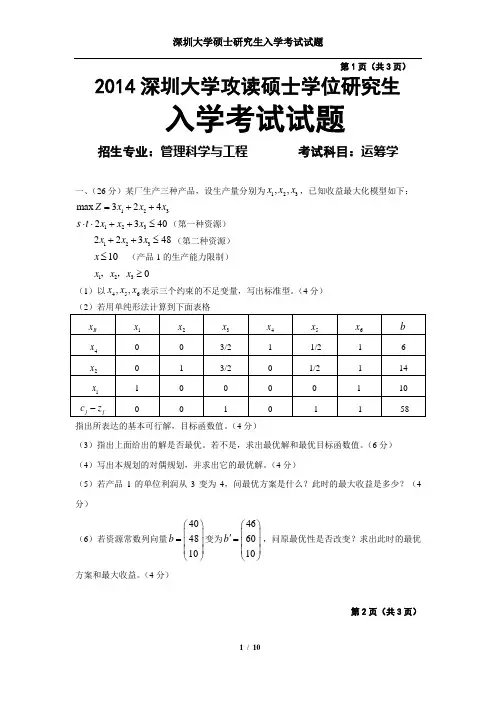
第1页（共3页）2014深圳大学攻读硕士学位研究生入学考试试题招生专业：管理科学与工程 考试科目：运筹学一、（26分）某厂生产三种产品，设生产量分别为123,,x x x ，已知收益最大化模型如下：123max 324Z x x x =++s t ⋅⋅1232340x x x ++≤（第一种资源）12322348x x x ++≤（第二种资源）10x ≤ （产品1的生产能力限制）1230x x x ≥，，（1）以456,,x x x 表示三个约束的不足变量，写出标准型。

（4分）指出所表达的基本可行解，目标函数值。

（4分）（3）指出上面给出的解是否最优。

若不是，求出最优解和最优目标函数值。

（6分） （4）写出本规划的对偶规划，并求出它的最优解。

（4分）（5）若产品1的单位利润从3变为4，问最优方案是什么？此时的最大收益是多少？（4分）（6）若资源常数列向量404810b ⎛⎫ ⎪= ⎪ ⎪⎝⎭变为466010b ⎛⎫⎪'= ⎪ ⎪⎝⎭，问原最优性是否改变？求出此时的最优方案和最大收益。

（4分）第2页（共3页）二、（24分）有123,,A A A 三个工厂，要把生产的产品运往123,,B B B 三个需求点。

若123,,B B B 三个需求点需求量没有得到满足，则单位罚款费用为6，3，4。

各厂的供应量、各点的需求量以及单位运价如下表。

问应如何组织调运才能使总费用（运输费用和罚款费用之和）最小？（1）请将此问题化为供需平衡的运输问题； （2）用最小元素法求（1）的一个初始调运方案； （3）判断（2）中的方案是否最优，并说明原因。

三、（22分）设货车按泊松流到达车站，卸货后马上离开。

已知平均每天到达4辆车。

该货站有2位工人，同时为货车卸货，假设卸货时间服从负指数分布，平均每天可服务6辆车。

求：（1）该货站没有货车卸货的概率。

（4分） （2）在货站排队等候卸货的平均货车数。

（4分） （3）每辆车在货站的平均逗留时间。

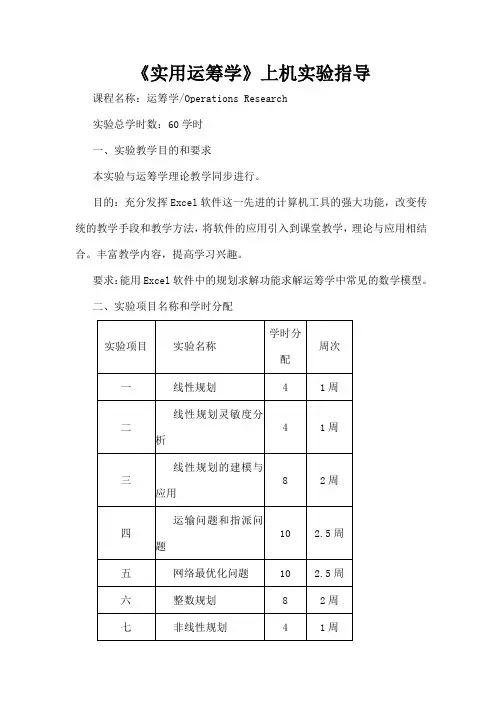
《实用运筹学》上机实验指导课程名称：运筹学/Operations Research实验总学时数：60学时一、实验教学目的和要求本实验与运筹学理论教学同步进行。

目的：充分发挥Excel软件这一先进的计算机工具的强大功能，改变传统的教学手段和教学方法，将软件的应用引入到课堂教学，理论与应用相结合。

丰富教学内容，提高学习兴趣。

要求：能用Excel软件中的规划求解功能求解运筹学中常见的数学模型。

二、实验项目名称和学时分配三、单项实验的内容和要求实验一线性规划（－）实验目的：安装Excel软件“规划求解”加载宏，用Excel软件求解线性规划问题。

（二）内容和要求：安装并启动软件，建立新问题，输入模型，求解模型，结果的简单分析。

（三）实例操作：求解习题1.1。

（1）建立电子表格模型：输入数据、给单元格命名、输入公式等；（2）使用Excel软件中的规划求解功能求解模型；（3）结果分析：如五种家具各生产多少？总利润是多少？哪些工序的时间有剩余，并对结果提出你的看法；（4）在Excel或Word文档中写实验报告，包括线性规划模型、电子表格模型和结果分析等。

案例1 生产计划优化研究某柴油机厂年度产品生产计划的优化研究。

某柴油机厂是我国生产中小功率柴油机的重点骨干企业之一。

主要产品有2105柴油机、x2105柴油机、x4105柴油机、x4110柴油机、x6105柴油机、x6110柴油机，产品市场占有率大，覆盖面广。

柴油机生产过程主要分成三大类：热处理、机加工、总装。

与产品生产有关的主要因素有单位产品的产值、生产能力、原材料供应量与生产需求情况等。

每种产品的单位产值如错误!未找到引用源。

所示。

表 C－1 各种产品的单位产值为简化问题，根据一定时期的产量与所需工时，测算了每件产品所需的热处理、机加工、总装工时，如表 C－2所示。

表 C－2 单位产品所需工时同时，全厂所能提供的总工时如表 C－3所示。

表 C－3 各工序所能提供的总工时产品原材料主要是生铁、焦碳、废钢、钢材四大类资源。

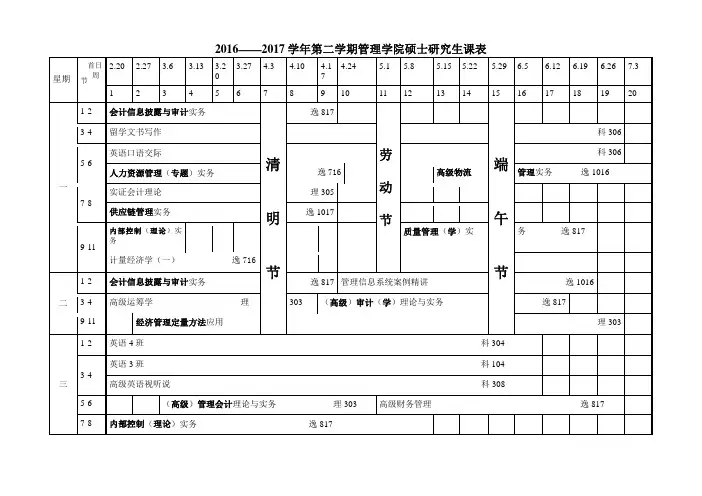
高级运筹学试题11（研究生）《高级运筹学》试题一、基本应用分析1．模型与解任写2个线性规划模型，模型必须覆盖线性规划所解决的两类问题，每个模型至少包括4个决策变量，约束条件至少4个以上且包含所有约束类型。

按下列要求完成：1）准确描述所解决的问题及数学模型；2）用软件进行求解，写出最优解、最优目标值、对偶问题的最优解；3）分析在保持最优解不变时，目标系数和右端常数的变化范围。

2. 决策分析问题结合所学专业方向，任意写出一个决策问题，该决策问题至少包含两个决策点，5个以上的状态点，用决策树法进行分析。

3. 运输问题（任选1题）1）设有三个煤矿供应四个地区的煤炭用量，而第三个矿区不能给第四个用煤地区供应煤炭。

各矿区的产量、各用煤地区的煤炭需求量及各矿区到各用煤地区的运价(万元/万吨)如下表。

按下列要求完成：1）列出该问题的产销平衡表；2）用最小元素法给出初始调运方案；3）求出总运费最少的调运方案。

B1 B2B3B4产量(万t) A1 26 18 22 27 350A234 23 19 35 560A329 20 23 ——450最低需求量430 370 100 200最高需求量550 450 230 不限2）某运输问题各产地产量、销地的销量及运输费用情况如下表：销地B1B2B3B4a i产地A1 5 9 2 3 60A2-- 4 7 8 40A3 3 6 4 2 30A4 4 8 10 11 50bj 20 60 35 45（1）求该最小化运输问题的最优解。

（2）假定B1的需要量是20-60之间，B2的需要量是50-70，求问题的最优解。

4．生产计划（任选1题）1）某公司面临一个是外包协作还是自行生产的问题。

该公司生产甲、乙、丙三种产品，这三种产品都要经过铸造、机加工和装配三个车间。

甲、乙两种产品的铸件可以外包协作，也可以自行生产，但产品丙必须本厂铸造才能保证质量。

相关资料见下表。

公司可利用的总工时为：铸造8000小时，机加工12000小时和装配10000小时。

第一题. 某工厂在计划期内要安排Ⅰ、Ⅱ两种产品的生产，已知生产单位产品所需的设备台时及A、B两种原材料的消耗、资源的限制，如下表：问题：工厂应分别生产多少单位Ⅰ、Ⅱ产品才能使工厂获利最多？线性规划模型：目标函数：Max z = 50 x1 + 100 x2约束条件：s.t. x1 + x2 ≤ 3002 x1 + x2 ≤ 400x2 ≤ 250x1 , x2 ≥ 0得到最优解：x1 = 50， x2 = 250最优目标值 z = 27500（作图略）第二题.某公司由于生产需要，共需要A，B两种原料至少350吨（A，B两种材料有一定替代性），其中A原料至少购进125吨。

但由于A，B两种原料的规格不同，各自所需的加工时间也是不同的，加工每吨A原料需要2个小时，加工每吨B原料需要1小时，而公司总共有600个加工小时。

又知道每吨A原料的价格为2万元，每吨B原料的价格为3万元，试问在满足生产需要的前提下，在公司加工能力的范围内，如何购买A，B两种原料，使得购进成本最低？解：目标函数： Min f = 2x1 + 3 x2约束条件：s.t. x1 + x2 ≥ 350x1 ≥ 1252 x1 + x2 ≤ 600x1 , x2 ≥ 0采用图解法。

如下图：得Q点坐标（250，100）为最优解第三题．某昼夜服务的公交线路每天各时间段内所需司机和乘务人员数如下设司机和乘务人员分别在各时间段一开始时上班，并连续工作八小时，问该公交线路怎样安排司机和乘务人员，既能满足工作需要，又配备最少司机和乘务人员解：设x i 表示第i班次时开始上班的司机和乘务人员数,这样我们建立如下的数学模型。

目标函数： Min x1 + x2 + x3 + x4 + x5 + x6约束条件：s.t. x1 + x6 ≥ 60x1 + x2 ≥ 70x2 + x3 ≥ 60x3 + x4 ≥ 50x4 + x5 ≥ 20x5 + x6 ≥ 30x1,x2,x3,x4,x5,x6 ≥ 0第四题．一家中型的百货商场，它对售货员的需求经过统计分析如下表所示。

《运筹学》实验指导书适用专业：工业工程东北大学秦皇岛分校控制工程学院工业工程专业2014年3月前言对于工业工程专业来说，运筹学是一门公共基础课，是应用性很强的课程。

它是利用现代数学研究各种资源的运用、筹划和相关决策等问题的一门重要学科，主要研究如何在一定条件下科学、合理地分配人力、物力、财力等资源，使实际系统有效运行。

它可以用来预测发展趋势，制定行动规划或优选方案，从而为行政管理人员和决策者在决策时提供科学的依据。

运筹学的实际运用包括如下六个步骤：问题分析；模型构造；模型求解；模型验证；解的有效控制；方案实施。

随着计算机软件的发展，许多复杂的运筹学计算可以由计算机软件来完成，如matlab、mathematica、lingo、excel等。

本实验课程以lingo软件为工具，使学生在学习了运筹学基本原理的基础上，进一步掌握使用软件工具解决运筹学实际问题的方法。

本实验课程共8学时，内容如下：1、软件编程基础及其在运筹学中的应用（2学时）2、单纯形法的计算机实现（2学时）3、解运输问题（2学时）4、解目标规划、整数规划问题和指派问题（2学时）实验一软件编程基础及其在运筹学中的应用（2学时）一、实验目的1、熟悉lingo的操作环境。

2、学会用lingo编程的方法来求解运筹学问题并读取结果。

二、实验素材例题1、（利润最大化问题）某工厂生产甲、乙两种产品。

每生产一个单位的甲产品需要使用A设备1小时，工人劳动时间1小时，可赢利20元；生产一个单位的乙产品需要使用B设备1小时，工人劳动时间2小时，可赢利30元。

受工厂条件限制，每天的总劳动时间不能超过120小时，A设备的总使用时间不能超过60小时，B设备的总使用时间不能超过50小时。

试建立线性规划模型，每天生产多少甲、乙产品，可使利润最大？解：建立线性规划模型。

设x1为每天生产甲产品的数量，x2为每天生产乙产品的数量。

由此得到线性规划模型：max=20*x1+30*x2;x1+2*x2<=120;x1<=60;x2<=50;x1>=0;x2>=0;将程序输入lingo软件，不需输入最后两行（变量的非负约束），点击solve 按钮，得到求解结果如下：Global optimal solution found. ---（已找到全局最优解）Objective value: 2100.000 ---（最优目标函数值） Infeasibilities: 0.000000 ---（找到的解违反了几个约束条件）Total solver iterations: 1 ---（迭代次数）Variable Value Reduced CostX1 60.00000 0.000000X2 30.00000 0.000000Row Slack or Surplus Dual Price1 2100.000 1.0000002 0.000000 15.000003 0.000000 5.0000004 20.00000 0.000000由上述结果得到，每天生产甲产品60个单位，乙产品30个单位，每天可获得的最大利润是2100元。

第一次课内实验题目1．生产计划问题已知某工厂计划生产I，II，III三种产品，各种产品需要在A，B，C三种设备上加工生产，具体相关数据如表，试研究下列问题：（1）如何充分发挥已有设备的能力，使生产盈利最大？（2）如果为了增加产量，可租用其它厂家设备B，每月可租用60台时，租金为1.8万元，试问租用设备B是否合算？（3）如果该厂家拟增加生产两种新产品IV和V，其中产品IV需用A设备12台时，B设备5台时，C设备10台时，单位产品盈利2100元；产品V需用A设备4台时，B设备4台时，C设备12台时，单位产品盈利1870元。

假设A，B，C三种设备台时不增加，试分别考虑这两种新产品的投产在经济上是否合算？（4）如果工厂对产品工艺进行重新设计改造，使改造后生产每件产品I需用A设备9台时，B设备12台时，C设备4台时，单位产品盈利4500元，试问这种改造方案对原计划有何影响？生产计划的相关数据2．快餐店用工问题某快餐店坐落在远离城市的风景区，平时游客较少，而每到双休日游客数量猛增，快餐店主要是为游客提供快餐服务，该快餐店雇用了两名正式员工，主要负责管理工作，每天需要工作8h，其余的工作都由临时工担任，临时工每天要工作4h。

双休日的营业时间为11:00到22:00，根据游客的就餐情况，在双休日的每天营业小时所需的职工数（包括正式工和临时工）如表所示。

营业时间与所需职工数量已知一名正式职工11：00开始上班，工作4h后休息1h，而后再工作4h；另一名正式职工13：00开始上班，工作4h后休息1h，而后再工作4h。

又临时工每小时工资为4元。

（1）在满足对职工需求的条件下，如何安排临时工的班次，使得使用临时工的成本最小？（2）如果临时工每班工作时间可以为3h，也可以为4h，如何安排临时工的班次，使得使用临时工的成本最小？这样比方案(1)能节省多少费用？此时需要安排多少临时工班次？2012级《运筹学》第一次课内实验题目3．轰炸方案问题某战略轰炸机群奉命摧毁敌人军事目标，已知该目标有四个要害部位，只要摧毁其中之一即可达到目标。

实验二线性规划模型的对偶问题及灵敏度分析一、实验目的：进一步掌握线性规划模型的基本原理，理解线性规划的对偶问题，掌握R软件在线性规划问题灵敏度分析中的运用。

二、实验内容：（1）教材P127 习题1。

利用线性规划的最终单纯形表，对目标函数系数和约束方程的常数项进行灵敏度分析，并在R软件中验证你的计算结果；（2）教材P131 习题11。

写出该问题的对偶问题，并用R 软件求解原问题和对偶问题。

指出二者最优解与对偶价格之间的联系。

（3）建立教材P130 习题7的数学模型并用R软件分析。

三、实验要求：（1）利用线性规划基本原理对所求解问题建立数学模型；（2）熟练写出线性规划问题的对偶问题；（3）给出R软件中的输入并求解；（4）对目标函数系数及约束方程的常数项进行灵敏度分析四、实验报告要求：实验过程描述（包括变量定义、分析过程、分析结果及其解释、实验过程遇到的问题及体会）。

（1）maxz=20X1+8X2+6X38X1+3X2+2X3<=2502X1+X2<=504X1+3X3<=150X 1,X2,X3>=0> library(lpSolve)> obj<-c(20,8,6)> mat<-matrix(c(8,3,2,2,1,0,4,0,3),nrow=3,byrow=T) > dir<-c("<=","<=","<=")> rhs<-c(250,50,150)> x<-lp("max",obj,mat,dir,rhs,compute.sens=1)> x$status;x$solution;x$objval[1] 0[1] 0 50 50[1] 700> x$sens.coef.from;x$sens.coef.to[1] -1e+30 6e+00 3e+00[1] 2.4e+01 1.0e+30 1.0e+30C1范围是（-∞，24），C2范围是（6，+∞），C3范围是（3，+∞）> library(lpSolve)> obj<-c(20,8,6)> mat<-matrix(c(8,3,2,2,1,0,4,0,3),nrow=3,byrow=T) > dir<-c("<=","<=","<=")> rhs<-c(250,50,150)> x<-lp("max",obj,mat,dir,rhs,compute.sens=1)> x$status;x$solution;x$objval[1] 0[1] 0 50 50[1] 700> x$duals;x$duals.from;x$duals.to[1] 0 8 2 -4 0 0[1] -1.000000e+30 7.105427e-15 -2.842171e-14 0.000000e +00 -1.000000e+30 -1.000000e+30[1] 1.0e+30 5.0e+01 1.5e+02 2.5e+01 1.0e+30 1.0e+30b1,b2,b3的对偶价格分别为0、8、2；b1范围为(250，∞)，b2范围为(0, 50)，b3范围为(0, 150)。