运筹学-大M法或两阶段法的上机实验

格式：doc
大小：179.02 KB
文档页数：11

下载文档原格式

管理运筹学两阶段法和大M法

两阶段法和大M法
阶段Ⅱ 求解原问题以阶段Ⅰ的最优基B作为原问题的初始可行基，求解原问题，得到原问题的最优基和最优解。例1 求解以下线性规划问题。
两阶段法和大M法
引进松弛变量x3，x4，x50，得到
增加人工变量x6，x7≥0，构造辅助问题，并进入第一阶段求解。
两阶段法和大M法
标准化并写出辅助问题的系数矩阵表：
x2 3 D 2 C B 1 A O 0 1 2
x1
基迭代路线
两阶段法和大M法
大M法的基本步骤如下：
（1）引进松弛变量，使约束条件成为等式；
（2）如果约束条件的系数矩阵中不存在一个单位矩阵，则引进人工变量；
（3）在原目标函数中，加上人工变量，每个人工变量
的系数为一个充分大的正数M；（4）用单纯形表求解以上问题，如果这个问题的最优解中有人工变量是基变量，则原问题无可行解。如果最优解中所有人工变量都离基，则得到原问题的最优解。
第二节单纯形法总结
• • • • •
LP的标准形式 LP的解的各种概念与形式单纯形法的原理单纯形法求解LP问题的步骤最终解的判别
将LP问题转化为标准形式单纯形表格法求解LP问题
下周见！
引进变量X4,X5
基中不包含单位矩阵，因此无法直接获得初始可行基。
• 人工变量法有两种方法：两阶段法和大M法。
两阶段法和大M法
引进人工变量 Xa=(xn+1,xn+2,…, xn+m)T
X=(x1,x2,…,xn)T
基础可行解 X=0,Xa=b
两阶段法和大M法
基本思想：
人造解 X0 不是原LP问题的基本可行解。但若能通过单纯形法的迭代步骤，将虚拟的人工变量都替换出去，都变为非基变量（即人工变量xn+1 = xn+2 = … = xn+m = 0），则X0的前n个分量就构成原LP问题的一个基本可行解。

《管理运筹学》02-4两阶段法和大m法

大M法的优势与局限性
优势
大M法能够处理大规模的整数规划问题，且计算过程相对简单，容易实现。
局限性
大M法只能求得问题的近似解，而非最优解，且当M值选取不合适时，可能导致求解结果偏离最优解较远。同时，对于一些特殊问题，如非线性、非凸等问题，大M法可能无法得到满意的结果。
04
大M法实施步骤
确定问题与目标
局限性
两阶段法需要花费更多的计算时间和资源，因为需要进行多次迭代和优化。此外，两阶段法对于初始解的选择比较敏感，如果初始解不好，可能会导致算法陷入局部最优解，而非全局最优解。
02
两阶段法实施步骤
阶段一：问题建模与求解
80%
确定问题目标
明确问题的目标，并将其转化为可量化的数学模型。
100%
建立数学模型
两阶段法案例
总结词
两阶段法是一种常见的求解线性规划问题的方法，通过将问题分解为两个阶段进行求解，可以找到最优解。
详细描述
在第一阶段，两阶段法首先确定一个初始解，然后通过迭代不断改进这个解，直到满足一定的收敛条件。在第二阶段，两阶段法使用一种称为对偶单纯形法的方法来求解子问
题，最终得到最优解。
大M法案例
输出求解结果，包括最优解、最优值等。
分析结果与决策
结果分析
对求解结果进行分析，包括最优解的合理性、最优值的可行性等。
制定决策方案
根据分析结果，制定相应的决策方案，包括最优解的实施方案、次优解的备选方案等。
方案评估与选择
对制定的决策方案进行评估和选择，确保方案符合实际需求和可行性。
05
案例分析
《管理运筹学》02-4两阶段法和大m法
目
CONTENCT

大M法和两阶段法课堂练习

1.4节中关于大M 法和两阶段法的课堂例题讨论课堂讨论题习题1.5(2)P.51 用大M 法和两阶段法求解,34233min 2121212121≥=+≤+≥++=x x x x x x x x x x z标准化后为,,,34233min 43212142132121≥=+=++=-++=x x x x x x x x x x x x x x z采用大M 法数学模型为,,,3423)(3min 62162142153216521≥=++=++=+-++++=x x x x x x x x x x x x x x x M x x z Λ单纯形表法求解如下：因此的最优解如下TX ]1030[*=，最优目标函数min z=3。

采用两阶段法。

第一阶段的数学模型是：,,,3423min 621621421532165≥=++=++=+-++=x x x x x x x x x x x x x x x Λω单纯形表法的求解如下第二阶段的数学模型基标准化了的模型。

通过第一阶段的计算，我们求得了一个可行基，即[]⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡-==001011101342P P P B ，解出相应的基变量后，可的单纯形表如下上述结果和将第一阶段的最后一张表的人工变量列删除，并且将原问题的价值系数换上再计算检验数的结果一样。

x入基，上述问题是退化问题，若按Bland法则，第一次换基时应让1相应的过程如下：已得第一阶段最优解，第二阶段的可行基是[]⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡-==011021111312P P P B初始单纯形表如下的最优解，与前述结果一样，但由于选择的换基次序不同（即寻优的方向不同），在第一阶段中多了一步迭代，同时第一阶段的最优解不是原问题（第二阶段）的最优解，又计算了一次迭代才得到最优解。

欢迎您的下载，资料仅供参考！致力为企业和个人提供合同协议，策划案计划书，学习资料等等打造全网一站式需求。

大M法和两阶段法

1
0 0 0 1 0 0 0 1 0 0 0
-1
3 2 5M-3 0 1 0 -2 0 1 0 -2
2
-7 -1 -8M+5 -1/3 -7/3 (11/3) 11/3M+7/3 0 0 1 0
-1
（3） 2 5M-1 0 1 0 0 0 (1) 0 0
0
1 0 0
0
0 1 0 0 0 1 0 → 2/3 5/2 →
→
两阶段法
第一阶段：引入辅助问题
max S x5 x6 x7 s.t. x1 x 2 2 x3 x 4 x5 2 2 x1 x 2 3 x3 x 4 x6 6 x1 x3 x3 x 4 x7 7 x j 0, j 1,2, ,7
Cj 段 ↓ -1 1
→ 基 x5
0 b 2
0 P1 （1）
0 P2 -1
0 P3 2
0 P4 -1
-1 P5 1
-1 P6 0
-1 Qi P7 0 2 → 注
-1
-1 Cj-Zj 0
x6
x7 → x1 x6 x7 → x1 x4
6
7 15 2 2 5 7 8/3 2/3
2
1 4 1 0 0 0 1 0
大M法

引入人工变量x5，x6，x7，将原问题化为
max F 2 x1 x 2 x3 x 4 M ( x5 x6 x7 ) s.t. x1 x 2 2 x3 x 4 x5 2 2 x1 x 2 3x3 x 4 x6 6 x1 x3 x3 x 4 x7 7 x j 0, j 1,2,,7
Cj-Zj 0

线性规划-大M法、两阶段法与几种特殊情况

进基变量的相持
出基变量的相持
max
z=
4x1
+2x2
-3x3
+5x4
s.t.
2x1
-x2
+ x3
+2x4
≥50
(1)
3x1
-x3
+2x4
80
(2)
x1
+x2
+x4
= 60
(3)
x1,
x2,
x3,
x4
≥ 0
1-4 线性规划- 大M法、两阶段法及几种特殊情况
单击添加副标题
单击此处添加文本具体内容，简明扼要地阐述你的观点
School of Business ECUST
单纯形法
单纯形法的一般思路+例子
单纯形表结构+例子
单纯形法的计算步骤
单纯形法的矩阵描述
大M法
两阶段法
几种特殊情况
无可行解
无界解
多重最优解
1
X3
0
-3 0 2 0 0 -2-M -M
σj
-1 0 1 0 1 -1 0
1
X5
0
0 0 1/2 3/2 0 -1/2-M -3/2-M
2
X5
0
-1 2+2M -M -M 0 0 0
σj
3/1
0 1 0 0 1 0 0
3
X5
0
X1 x2 x3 x4 x5 x6 x7
3/2
X2
2
1/2/1/2
1 0 -1/2 1/2 0 1/2 -1/2
1/2

线性规划-大M法、两阶段法与几种特殊情况课件

0 1 001 -1 2+2M -M -M 0
00 00
3 3/1
2 0 -1 1 0 1 -1
1 1/2
-1 1 0 -1 0 0 1
1
-
1 0 0 1 1 0 -1
2 2/1
1+2M 0 -M 2+M 0 0 -2-2M
1 0 -1/2 1/2 0 1/2 -1/2
1/2
0 1 -1/2 -1/2 0 1/2 1/2
-Mx7
-Mx8
s.t.
2x1
-x2
+ x3
+2x4
－x5
+x7
=50
(1)
3x1
-x3
+2x4
+x6
= 80
(2)
x1
+x2
+x4
＋x8
= 60
(3)
x1,
x2,
x3,
x4,
x5,
x6,
x7,
x8 ≥ 0
添加人工变量
min z=
4x1
+2x2
-3x3
+5x4
+Mx7
+Mx8
s.t.
2x1
-x2
+ x3
max z= 4x1 +2x2 -3x3 +5x4
s.t.
2x1 -x2 + x3 +2x4 －x5
=50 (1)
3x1
-x3 +2x4
+x6 = 80 (2)
x1 +x2
+x4
x1, x2, x3, x4, x5,

线性规划-大M法、两阶段法与几种特殊情况

x4,
x5,
x6,
x7,
x8 ≥ 0
School of Business ECUST
添加人工变量
min z=
4x1
+2x2
-3x3
+5x4
+Mx7
+Mx8
s.t.
2x1Hale Waihona Puke -x2+ x3
+2x4
－x5
+x7
=50 (1)
3x1
-x3
+2x4
+x6
= 80 (2)
x1
+x2
+x4
＋x8
= 60 (3)
x1,
x2,
x3,
x4,
x5,
x6,
x7,
x8 ≥ 0
School of Business ECUST
4 2 -3 5
0
0 MM
CB XB
[ x1]
x2
x3
x4
x5
x6 x7 x8 b
M [ x7]
2
-1
1
2
-1 0 1 0 50
0 x6
3 0 -1 2
0
1 0 0 80
M x8
1 10
1
0
0 0 1 60
1 0 0 1 1 0 -1
1+2M 0 -M 2+M 0 0 -2-2M
1 0 -1/2 1/2 0 1/2 -1/2
0 1 -1/2 -1/2 0 1/2 1/2
0 0 1/2 1/2 1 -1/2 -1/2
0 0 1/2 3/2 0 -1/2-M -3/2-M

02大M法和两阶段法

X* = (4，1，9，0，0)T, z* = 2
M-1 3M-1* 0 -M 0 0 -2 0 1 0 0 -1 [1] 0 0 -1 1 -2 0 1 0 0 0 1 M-1* 0 0 -M 0 -3M+1 0 0 1 -2 2 -5 1 0 0 -1 1 -2 0 1 0 0 0 1 0 0 0 -1 1-M -M-1 0 0 1/3 -2/3 2/3 -5/3 1 0 0 -1 1 -2 0 1 2/3 -4/3 4/3 -7/3 0 0 -1/3 -1/3 -M+1/3 -M+2/3
-1 x3 0 0 1 0 0 0 1 0
0 x4 1 0 0 0 1/3 0 2/3 -1/3
0 x5 -2 -1 0 -1 - 2/3 -1 - 4/3 -1/3
XB x4 x2 x3 x1 x2 x3

4 — —
X* = (4，1，9，0，0)T,
z* = 2
5. 2 线性规划问题解的讨论
线性规划解除有唯一最优解的情况外，还有如下几种情况
§ 6 应用举例
• P38
迭代运算 .用非基变量xk替换换出变量 .对主元素行(第l行) 令 bl/alk→bl;alj/alk→ajl 对主元素列(第k列)令1→alk;0→其它元素表中其它行列元素令 aij-ali/alk· aik→aij bi-bl/alk· aik→bi б j- alj/alk·б k → б j
z =3x1-x2-x3
’
在第一阶段的最优单纯形表中删除人工变量列，并把目标函数系数替换为原问题的目标函数系数，计算出检验数，用单纯形法求解。
cj CB 0 -1 -1 σ 3 -1 -1 σ
j j

运筹

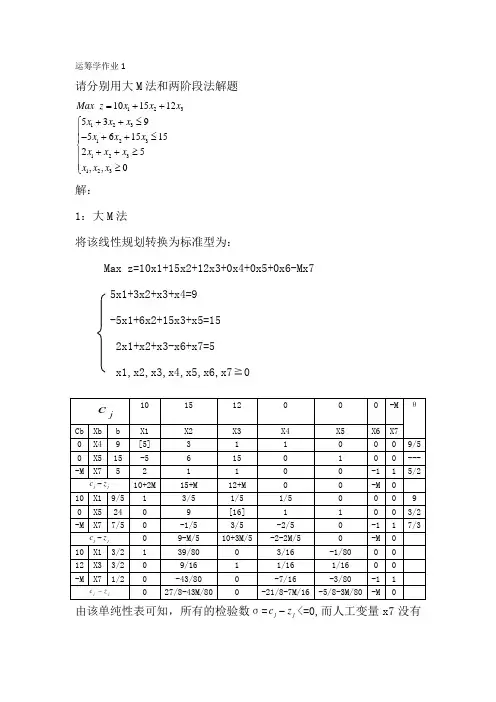
运筹学作业1请分别用大M 法和两阶段法解题12312312312312310151253956151525,,0Max z x x x x x x x x x x x x x x x =++++≤⎧⎪-++≤⎪⎨++≥⎪⎪≥⎩解： 1：大M 法将该线性规划转换为标准型为：Max z=10x1+15x2+12x3+0x4+0x5+0x6-Mx75x1+3x2+x3+x4=9 -5x1+6x2+15x3+x5=15 2x1+x2+x3-x6+x7=5 x1,x2,x3,x4,x5,x6,x7≧0由该单纯性表可知，所有的检验数σ=j j z c -<=0,而人工变量x7没有被迭代出去，x7=1/2≠0,所以原线性规划问题无可行解。

2：阶段法： Min ω=X7 5x1+3x2+x3+x4=9 -5x1+6x2+15x3+x5=15 2x1+x2+x3-x6+x7=5 X1,x2.x3,x4,x5,x6,x7≧0由表中最后一行的检验数可知：所有的非基变量检验数σ=j j z c -=0,而人工变量x7=1/2≠0,并没有被迭代出去，故原线性规划问题无可行解。

运筹学作业22.某职工从武汉调至上海工作，拟将行李用集装箱装箱，然后用汽车或轮船运往上海，目的是为了节省运费但只能任选其一种运输方式。

已知有关数据见下表：试引入整数变量和0-1决策变量等建立该问题的整数规划模型解：设X1，X2分别是甲乙货物的箱数，同时引入一个充分大的数M 以及0-1变量y,令：0,当采取车运方式y=1,当采取船运方式则该整数规划可用如下模型表示：Min z = (1-y)(100x1+150x2)+y(200x1+300x2)7x1+8x2≤35+yM20x1+15x2≤500+yM80x1+75x2≤85+(1-y)M35x1+42x2≤250+(1-y)MX1,X2整数。

两阶段法法

i
inf 45
1
7 7
45
1
7
7
0
第二阶段
cj CB
-3 -2
-2
-3
5
0
i
XB x2 x1 z
b
x1 7 7
0 1 0
x2
1 0 0
x3 1 6 7 7 7
x4 1 7 7 inf 45 7
4
45
1 1
50
7
由表可以看出线性规划有唯一的最优解。 ⑵
min z 2 x1 3 x 2 x3 x1 4 x2 2 x3 8 3 x1 2 x2 6 x , x , x , 0 2 3 1
3
云南大学数学与统计学院实c(xb(i)); end while(flag) for i=1:n t=0; for j=1:m t=t+a(j,i)*CB(j); end cz(i)=c(i)-t; %计算检验数 cz end flag=0; for i=1:n if cz(i)<0 flag=1; break; elseif flag==0 end end [zuixiao,wz]=min(cz); %记录最小的检验数与位置 for i=1:m if a(i,wz)>0 o(i)=b(i)/(a(i,wz)); %o 为用规则计算的 bi/aik else o(i)=inf; %定义负值为无穷大 end end [s,owz]=min(o); %记录最小的，及其位置 %*---------单位化主列，并将 a 各列与 b 进行初等变换-----* temp=a(owz,wz); b(owz)=b(owz)/temp; for j=1:n a(owz,j)=a(owz,j)/temp; end for i=1:m if i~=owz bs=a(i,wz)/a(owz,wz);%bs 为初等变换时引入的对应行相差的倍数 b(i)=b(i)-bs*b(owz); for j=1:n a(i,j)=a(i,j)-bs*a(owz,j); end end

1.4线性规划单纯形大M法及2阶段(经典运筹学)

可得一个初始基本可行解
1 − 1 6 − 1 0 A= 1 1 2 0 − 1
但对线性规划问题 max z = − 5 x1 − 21 x 3 s.t x1 − x 2 + 6 x 3 − x 4 = 2 x1 + x 2 + 2 x 3 − x 5 = 1 x1 , x 2 , x 3 , x 4 , x 5 ≥ 0
若不然，原问题（1）有可行解
x1 , x 2 L , x n ≥ 0
不设 1 = d1, x2 = d2 ,L, xn = dn 妨 x 为 1 的个行（）一可解则 * = (d1, d2 ,L n ,0,0,L ) X d 0 是 2 的行（）可解
max S = − xn+1 − xn+ 2 − L − xn+ m
max S = − xn+1 − xn+ 2 − L − xn+ m
∴X = (d1, d2 ,L n ) d 是1 的个行 () 一可解
且 1, d2 L, dn ≥ 0 d
可证X是基本可行解
x 1 , x 2 L , x n , x n +1 , L , x n + m ≥ 0
[例]求线性规划问题的解解：做辅助线性规划问题 max z = −5x1 − 21x3 max S = − x 6 − x 7 s.t x1 − x2 + 6 x3 − x4 = 2 = − 3 + 2 x1 + 8 x 3 − x 4 − x 5 x1 + x2 + 2 x3 − x5 = 1 s .t x1 − x 2 + 6 x 3 − x 4 + x 6 = 2 x1 , x2 , x3 , x4不是典则形式 , x5 ≥ 0 x1 + x 2 + 2 x 3 − x 5 + x 7 = 1 x1 , x 2 , x 3 , x 4 , x 5 , x 6 , x 7 ≥ 0

运筹学及其应用3.3 大M法和两阶段法

6
1 1 1 1 0 0 0 4
T
=

−2 0 0
1 3 0
−1 1 0
0 0 0
−1 0 0
1 0 1
0 1 1
1 09
1 1 1 1 0 0 0 4
→

−2 0 2
1 3 −1
−1 1 1
0 0 0
−1 0 1
1 0 0
0 1 1
1 −91
1
v 两阶段法的第一阶段求解一个目标中只包含人工变量的LP问题，即令目标函数中其它变量的系数取零，人工变量的系数取某个正的常数（一般取 1），在保持原问题约束不变的情况下求这个目标函数极小化的解。
v 显然在第一阶段中，当人工变量取值为0时，目标函数值也为0。这时候的最优解就是原问题的一个基可行解。如果第一阶段求解结果最优解的目标函数值不为0，也即最优解的基变量中含有非零的人工变量，表明原LP问题无可行解。
5
例：
min Z = 3x1 + 0x2 − x3 + 0x4 + 0x5 + Mx6 + Mx7
第1阶段：
min ω = x6 + x7

x1 −2 x1

+ x2 + x3 + x2 − x3 3 x2 + x3
+ x4
− x5 + x6
+ x7
=4 =1 =9
x1~5
≥0
对单纯形矩阵作初等行变换，有：
1 0 0
0 1 0
0 0 0
−1/ 4 3/4 3/4
5/ 2
3 3
/ /

运筹学大M法和两阶段法

第二节大M法和两阶段法
如果线性规划模型中约束条件系数矩阵中不存在单位向量组，解题时应先加入人工变量，人工地构成一个单位向量组。
人工变量只起过渡作用，不应影响决策变量的取值。
两种方法可控制人工变量取值。
大M法两阶段法
例
min F 3 x1 x2 x3 s.t. x1 2 x2 x3 11 4 x1 x2 2 x3 3 2 x1 x3 1 x j 0, j 1,2,3
→
4M
-6M+3
M-1
3M-1
0
-M
0
0
Cj 段 ↓
→
0
3
-1
-1
0
0
-M
-M Qi 注
基
b
P1
P2
P3
P4
P5
P6
P7
0
x4
11
1
-2
1
1
0
0
0
11
1
-M
x6
3
-4
1
2 （1）
0
-1
1
0
3/2 →
-M
x7 →
1
-2
0
0
0
0
1
1
Cj-Zj
4M
-6M+3
M-1
3M-1
0
-M
0
0
0
x4
0
2
-M
x6
0
-1
解题过程
Cj
→ 基 x5 x6 x7 → x5
0 b 11 3 1 4 10
P7 0 0 1 0 -1 11 3/2 1

2最优化教案(两阶段法与大M法)

§4.2 两阶段法与大M 法————初始可行基的求法求解线性规划的步骤是： 1）已知一个初始基本可行解 2）从初始基本可行解出发，写出单纯型表，求出进基离基变量，做主元消去法，求出一个新的基本可行解且使目标函数值得到改善。

3）判断当前基本可行解是否是最优解那末，当观察不出来初始基本可行解时，怎么办？下面介绍的方法是几种求初始基本可行解的方法4.2.1 两阶段法mincxt s .b Ax =x ≥0其中A 是nm ⨯矩阵，b≥0。

若A 中有m 阶单位矩阵，则初始基本可行解立即得到。

比如，[]N I A m ,=，那么⎥⎦⎤⎢⎣⎡=⎥⎦⎤⎢⎣⎡=0b x x x N B就是一个基本可行解。

若A 中不包含m阶单位矩阵，就需要用某种方法求出一个基本可行解。

介绍两阶段法之前，先引入人工变量的概念。

设A 中不包含m阶单位矩阵，为使约束方程的系数矩阵中含有m阶单位矩阵，把每个方程增加一个非负变量，令b x Ax a =+ （4.2.2）x ≥0 ，a x ≥0即bx x I A a m =⎥⎦⎤⎢⎣⎡),( （4.2.3）x ≥0 ，ax≥0显然，⎥⎦⎤⎢⎣⎡=⎥⎦⎤⎢⎣⎡b x x a 0是4:2:3的一个基本可行解.向量x ®¸0是人为引入的，它的每个分量成为人工变量。

人变量与前面介绍过的松弛变量是两个不同的概念。

松弛变量的作用是把不等式约束改写成等式约束，改写前后的两个问题是等价的。

因此，松弛变量是“合法”的变量。

而人工变量的引入，改变了原来的约束条件从这个意义上讲，它们是“不合法”的变量。

第一阶段是用单纯形方法消去人工变量（如果可能的话）：min a Tx es:t A x +x ®=b (4:2:1) x ¸0;x ®¸0其中e =(1;1;1;¢¢¢;1)T 是分量全是1的m 维列向量，x ®=(x n+1;¢¢¢;x n+m )T 是人工变量构成的m 维列向量。

1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

实验报告实验课程名称运筹学
实验项目名称大M法或两阶段法的上机实验年级
专业
学生姓名
学号
00 学院
实验时间：年月日
实验内容（包括实验具体内容、算法分析、源代码等等）：
1.书上P97页第6题：用大M 法和两阶段法求解下列线性规划问题。

max z=5；3213x x x ++ 约束条件：102x 4x x 321≥++， 16.x 2x -x 321≤+ A ：大M 法
图1.1
图1.2
δ，得出目标函数的最优解x1=16，x2=0，由上面的结果可知，满足所求出的0
≤
j
x3=0，sx4=16，Rx5=0，sx=0，最优值是80。

当把M的值改为100000后，值还是一样的，这样就可以得出当M为100时，已经得出有效解。

B：两阶段法
图1.3
由图1.3可知，先进行线性规划的第一阶段，满足0≤j δ，且z 值为零，即说明存在一个可行解使得所有的人工变量都为零，此时x2=2.5，sx6=21，其余为0得出z=0。

接下来进行第二阶段，令z=5x1+x2+3x3-0sx4+0Rx5+0sx6，和大M 的分析方法一样，最终将得到满足0≤j δ时达到最优解：当x1=16，x2=0，x3=0，sx4=6，Rx5=0，sx6=0，最优值为80。

2.书上P97页第7题（4）大M 法和两阶段法求解下列线性规划问题。

max z=；321x x 2x ++ 约束条件：，42x 2x 4x 321≥++ ，204x 2x 21≤+ ，162x 8x 4x 321≤++ A ：大M 法
图2.1
图2.2
由上面的图 2.1可知，首先先输入数据即线性规划的系数如图 2.1所示令max z=321x x 2x ++-0sx4+0sx6+0sx7-MRx5；进行下一次迭代，以同样的方法一直下去，直到所求出的为止0≤j δ，就可以得出目标函数的最优解：x1=4，sx4=12，sx6=12，其余为0时，最优值为8。

当把M 的值改为100000后，值还是一样的，这样就可以得出当M 为100时，已经得出有效解。

B：两阶段法
图2.3
10。

运筹学-大M法或两阶段法的上机实验

合集下载

管理运筹学两阶段法和大M法

《管理运筹学》02-4两阶段法和大m法

大M法和两阶段法课堂练习

大M法和两阶段法

线性规划-大M法、两阶段法与几种特殊情况

线性规划-大M法、两阶段法与几种特殊情况课件

线性规划-大M法、两阶段法与几种特殊情况

02大M法和两阶段法

运筹

两阶段法法

1.4线性规划单纯形大M法及2阶段(经典运筹学)

运筹学及其应用3.3 大M法和两阶段法

运筹学大M法和两阶段法

2最优化教案(两阶段法与大M法)

文档推荐

最新文档