全等三角形的存在性问题针对演练

一、八年级数学全等三角形解做题压轴题〔难〕1. 〔1〕如图〔1〕,：在△ ABC中,N BAC=90.,AB二AC,直线m经过点A, 8口,直线m, CE J_直线m,垂足分别为点D、E.证实:DE=BD+CE.〔2〕如图〔2〕,将〔1〕中的条件改为：在△ ABC中,AB=AC, D、A、E三点都在直线m 上,并且有N BDA=Z AEC=Z BAC=.,其中.为任意锐角或钝角.请问结论DE=BD+CE是否成立? 如成立,请你给出证实;假设不成立,请说明理由.〔3〕拓展与应用：如图〔3〕 , D、E是D、A、E三点所在直线m上的两动点〔D、A、E 三点互不重合〕,点F为N BAC平分线上的一点,且△ ABF和^ ACF均为等边三角形,连接BD、CE,假设N BDA=Z AEC=Z BAC,试判断△ DEF 的形状.【答案】(1)见解析(2)成立(3) 4DEF为等边三角形【解析】解：(1)证实：BDL直线m, CEJ_直线m,,N BDA=N CEA=900.: Z BAC=90°, /. Z BAD+Z CAE=90°.•/ Z BAD+Z ABD=90°, /. Z CAE=Z ABD.又AB二“AC〞,「・△ ADB合△ CEA (AAS) . /. AE=BD, AD=CE./. DE=,,AE+AD=H BD+CE.(2)成立.证实如下：: Z BDA =Z BAC=a , /. Z DBA+Z BAD=Z BAD+Z CAE=180°-O r . /. Z DBA=Z CAE.Z BDA=Z AEC=., AB=AC,「・△ AD於△ CEA (AAS). /. AE=BD, AD=CE.DE二AE+AD=BD+CE.(3)△ DEF为等边三角形.理由如下：由(2)知,△ ADB合△ CEA, BD=AE, Z DBA =Z CAE,: △ ABF 和^ ACF 均为等边三角形,J Z ABF=Z CAF=60°.・•, Z DBA+Z ABF=Z CAE+Z CAF. /. Z DBF=Z FAE.; BF=AF,,•・丛DBF合△ EAF (AAS) . /. DF=EF, Z BFD=Z AFE.・•, Z DFE=Z DFA+z AFE=Z DFA+Z BFD=60°.・•.A DEF为等边三角形.(1)由于DE=DA+AE,故由AAS证△ ADB合4 CEA,得出DA=EC, AE=BD,从而证得DE=BD+CE.(2)成立,仍然通过证实△ ADB2 J CEA,得出BD=AE, AD=CE,所以DE=DA+AE=EC+BD.(3)由△ ADB2△ CEA得BD=AE, NDBA=N CAE,由△ ABF和△ ACF均等边三角形,得Z ABF=Z CAF=60°, FB=FA,所以N DBA+N ABF=N CAE+N CAF,即N DBF二N FAE,所以△ DBF^ △ EAF,所以FD=FE, Z BFD=Z AFE,再根据N DFE=Z DFA+Z AFE=Z DFA+Z BFD=60°得到△ DEF是等边三角形.2.如图1,在正方形ABCD中,P是对角线BD上的一点,点E在AD的延长线上,且PA=PE, PE 交CD 于 F〔1〕证实：PC=PE；〔2〕求N CPE的度数：〔3〕如图2,把正方形ABCD改为菱形ABCD,其他条件不变,当N ABC=12〔T时,连接【答案】(1)证实见解析(2) 90° (3) AP=CE【解析】【分析】(1)、根据正方形得出AB=BC, ZABP=ZCBP=45%结合PB=PB得出aABP g^CBP,从而得出结论：⑵、根据全等得出NBAP=NBCP, ZDAP=ZDCP,根据PA=PE得出NDAP=NE,即ZDCP=ZE,易得答案；(3)、首先证实4ABP和^CBP全等,然后得出PA=PC, NBAP=NBCP,然后得出NDCP二NE,从而得出NCPF=NEDF=60°,然后得出AEPC是等边三角形,从而得出AP=CE.【详解】⑴、在正方形ABCD 中,AB=BC, ZABP=ZCBP=45%在ZkABP 和4CBP 中,XV PB=PB AAABP^ACBP (SAS) , ,PA=PC, VPA=PE>:.PC=PE；⑵、由(1)知,A ABP^ACBP,.\ZBAP=ZBCP, JNDAP=NDCP,VPA=PE, .\ZDAP=ZE> /. ZDCP=ZE. VZCFP=ZEFD (对顶角相等), A180° - ZPFC - ZPCF=1800 - ZDFE - NE, BPZCPF=ZEDF=90<>：⑶、AP = CE理由是：在菱形ABCD 中,AB=BC, NABP二NCBP,在2\ABP ^lACBP 中,XV PB=PB /.△ABP^ACBP (SAS),,PA二PC, NBAP=NDCP,VPA=PE,,PC=PE,,NDAP=NDCP, V PA=PC,/DAP=NE, A ZDCP=ZE V ZCFP=ZEFD (对顶角相等),A180°- ZPFC - ZPCF=180° - ZDFE - NE, RPZCPF=ZEDF=180° - ZADC=180° - 120°=60°, AAEPC 是等边三角形,,PC=CE, AAP=CE考点：三角形全等的证实3.如图,在AA8C中,NAC8为锐角,点£＞为射线8C上一动点,连接AO.以AO为直角边且在AD的上方作等腰直角三角形ADF.图①图②图③〔1〕假设A3 = AC, ABAC = 90°①当点.在线段BC上时〔与点3不重合〕,试探讨CF与8.的数量关系和位置关系：②当点O在线段C的延长线上时,①中的结论是否仍然成立,请在图2中而出相应的图形并说明理由；〔2〕如图3,假设ABwAC, ABAC90° , ZBC4 = 45°,点.在线段8C上运动,试探究CF与8.的位置关系.【答案】〔1〕①CF_LBD,证实见解析：②成立,理由见解析：〔2〕 CF1BD,证实见解析.【解析】【分析】〔1〕①根据同角的余角相等求出NCAF=NBAD,然后利用"边角边"证实4ACF和4ABD全等,②先求出NCAF=NBAD,然后与①的思路相同求解即可：〔2〕过点A作AE_LAC交BC于E,可得4ACE是等腰直角三角形,根据等腰直角三角形的性质可得AC=AE, NAED=45.,再根据同角的余角相等求出NCAF=NEAD,然后利用“边角边〞证实4ACF 和4AED全等,根据全等三角形对应角相等可得NACF=NAED,然后求出ZBCF=90°,从而得到CFJ_BD.【详解】解：〔1〕①•••NBAC=90°, 4ADF是等腰直角三角形,.\ZCAF+ZCAD=90% ZBAD+ZACD=90°,.\ZCAF=ZBAD,在4ACF和4ABD中,VAB=AC, ZCAF=ZBAD, AD=AF,.,.△ACF^AABD〔SAS〕,.・.CF=BD, ZACF=ZABD=45",ZACB=45",AZFCB=90°,.-.CF±BD：②成立,理由如下：如图2：VZCAB=ZDAF=90%,ZCAB+ ZCAD= ZDAF+ ZCAD, 即NCAF=NBAD,在aACF和AABD中,VAB=AC, ZCAF=ZBAD, AD=AF, AAACF^AABD(SAS), ACF=BD, NACF=NB,VAB=AC, ZBAC=90%AZB=ZACB=45%/. Z BCF= ZACF+ ZACB=45o+45o=90°,ACF1BD：(2)如图3,过点A作AE_LAC交BC于E,•/ ZBCA=45",••.△ACE是等腰直角三角形,,AC=AE, NAED=45°, VZCAF+ZCAD=90°, ZEAD+ZCAD=90%,NCAF=NEAD,在4ACF和4AED中,VAC=AE, NCAF=NEAD, AD=AF,.•.△ACF^AAED(SAS), /. ZACF=ZAED=45\,ZBCF= ZACF+ ZBCA=45o+45°=90°, ACF1BD.【点睛】此题考查全等三角形的动点问题,综合性较强,有一定难度,需要熟练掌握全等三角形的判定和性质进行综合运用.4.如图〔1〕,在△A3C中,ZA = 90°, A3 = AC,点.是斜边8C的中点,点E, 产分别在线段A3, 4c上,且NEDF = 90..〔1〕求证：△.所为等腰直角三角形：〔2〕假设△ABC的面积为7,求四边形AEDF•的面积：〔3〕如图〔2〕,如果点E运动到A8的延长线上时,点尸在射线C4上且保持ZEDF = 90°,△.石尸还是等腰直角三角形吗.请说明理由.【答案】〔1〕证实见解析；〔2〕 3.5：〔3〕是,理由见解析.【解析】【分析】〔1〕由题意连接AD,并利用全等三角形的判定判定△ BD年△ ADF〔ASA〕,进而分析证得△.瓦'为等腰直角三角形；〔2〕由题意分析可得S网边形AEDF=S MDF+S AADE=S ABDE+S ACDF,以此进行分析计算求出四边形AEDF的面积即可；〔3〕根据题意连接AD,运用全等三角形的判定判定△ BDE^ △ ADF〔ASA〕,进而分析证得△.所为等腰直角三角形.【详解】解：〔1〕证实：如图①,连接AD.「N BAC=90°,AB=AC,点D是斜边BC的中点,/. AD±BC , AD=BD,・•, Z 1=Z B=45°,Z EDF=90% Z 2+Z 3=90%又,Z 3+Z 4=90°,/. Z 2=Z 4,在^ BDE 和^ ADF 中,Z 1=Z B, AD=BD,Z 2=Z 4,/. △ BDE合 , ADF(ASA),・•, DE二DF,又；Z EDF=90\・•・ ADEF为等腰直角三角形.(2)由(1)可知DE=DF, NON 6=45., 又「N 2+N 3=90°, Z 2+Z 5=90%J Z 3=Z 5,A ADE级△ CDF,・' S N边H,AEDF=S AADF+S CADE二S ABDE+S^CDF,S MBC=2 S 网边毛AEDF,S wijn；AEDF=3.5.(3)是,如图②,连接AD.•/ Z BAC=90\ AB=AC, D 是斜边BC 的中点,/. AD±BC Z AD=BD ,「・Z 1=45°,Z DAF=180°-Z l=180°-45°=135% Z DBE=180°-Z ABC=180°-45°=135%/. Z DAF=Z DBE,「Z EDF=90\/. Z 3+Z 4=90%又；Z 2+Z 3=90°,「・Z 2=Z 4,在仆BDE 和a ADF 中,Z DAF=Z DBE, AD=BD,N 2=Z 4,△ BDE合△ ADF(ASA),・•.DE=DB又：Z EDF=90\.•.A DEF为等腰直角三角形.【点睛】此题考查等腰直角三角形的性质以及全等三角形的判定与性质,根据题意作辅助线构造出全等三角形是解题的关键.5.如图,在MBC中,ZC = 90°, AC = 3, BC = 7,点.是8c边上的动点,连接AD,以AO为斜边在A.的下方作等腰直角三角形AO石.(1)填空：AABC的面积等于—；(2)连接CE,求证：CE是NAC3的平分线；(3)点.在6C边上,且CO = 1,当.从点.出发运动至点3停止时,求点E相应的运动路程.王O 1 _【答案】〔I〕—：〔2〕证实见解析：〔3〕 3点【解析】【分析】〔1〕根据直角三角形的面积计算公式直接计算可得：〔2〕如下图作出辅助线,证实△AEM名ADEN 〔AAS〕,得至I] ME=NE,即可利用角平分线的判定证实：〔3〕由〔2〕可知点E在NACB的平分线上,当点D向点B运动时,点E的路径为一条直线,再根据全等三角形的性质得出CN=!〔AC + C.〕,根据CD的长度计算出CE的长度即可.【详解】解：〔1〕 ZC = 90°, AC = \ BC = 7= -ACxBC = -x3x7 = — ,故答案为：—2〔2〕连接CE,过点E作EMLAC于点M,作EN_LBC于点N,AZEMA=Z END=90°,XVZACB=90SAZMEN=90%AZMED+Z DEN=90°,•••△ADE是等腰直角三角形AZAED=90\ AE=DEA ZAEM+Z MED=90%, ZAEM=Z DEN,在△AEM 与ZkDEN 中,ZEMA=Z END=90% ZAEM=Z DEN, AE=DEAAAEM^ADEN 〔AAS〕/. ME=NE,点E 在NACB 的平分线上, 即CE 是NAC3的平分线工(3)由(2)可知,点E 在NACB 的平分线上,・•・当点D 向点B 运动时,点E 的路径为一条直线,VAAEM^ADEN,AM=DN,即 AC-CM=CN-CD在 RtZiCME 与 RtZkCNE 中,CE=CE, ME=NE,ARtACME^RtACNE (HL)ACM=CN.,.CN=；(AC + CO),又YNMCE 二NNCE=45°, ZCME=90\・,. CE= y/2CN = —(AC + CD).2当 AC=3, CD=CO=1 时,CE=](3 + 1) = 2&当 AC=3, CD=CB=7 时,5CE=r (3 + 7) = 5 虚,点E 的运动路程为：50-20 = 30,£【点睛】此题考查了全等三角形的综合证实题,涉及角平分线的判定,几何中动点问题,全等三角 形的性质与判定,解题的关键是综合运用上述知识点.6.如图1,在长方形ABCD 中,AB=CD=5 cm, BC=12 cm,点P 从点B 出发,以2cm/s 的 速度沿BC 向点C 运动,设点P 的运动时间为ts.(1) PC=—cm ：(用含t 的式子表示)■I) I)(2)当t 为何值时,△ABPg^DCP?.(3)如图2,当点P从点B开始运动,此时点Q从点C出发,以vcm/s的速度沿CD向点D运动,是否存在这样的v值,使得某时刻4ABP与以P, Q, C为顶点的直角三角形全等？假设存在,请求出v的值：假设不存在,请说明理由.【答案】(1) (12-2/)； (2)1 = 3;(3)存在,P = 2或忏1【解析】【分析】(1)根据P点的运动速度可得BP的长,再利用BC的长减去BP的长即可得到PC的长：(2)先根据三角形全等的条件得出当BP=CP,列方程求解即得；(3)先分两种情况：当BP=CQ, AB=PC 时,△ABPgZ\PCQ：或当BA=CQ, PB=PC 时,△ABPgaQCP,然后分别列方程计算出t的值,进而计算出v的值.【详解】解：(1)当点P以2cm/s的速度沿BC向点C运动时间为ts时3P = 2/57•・• BC = \2cin：.PC = BC-BP = (n-2i)cm故答案为：(12—27)(2) MBP = ^DCP・•. BP = CP・•・ 2/= 12-2/解得1 = 3.(3)存在,理由如下：①当BP=CQ, AB=PC 时,ZiABP名△PCQ,1. PC=AB=5.•.BP=BC-PC=12-5=7•・• BP = Item：.2t=7解得t=3.5.\CQ=BP=7,那么 3.5v=7解得y = 2.②当B4 = C.,PB = PC 时,MBP = \QCP,: BC = ncm,BP = CP = -BC = 6c7〃 2V BP = Item:.2t = 6解得/ = 3CQ = 3vcm,: AB = CQ = 5cm, 3v = 5解得U3综上所述,当u = 2或i,=,时,A48尸与以P, Q,C为顶点的直角三角形全等.【点睛】此题考查全等三角形的判定及性质和矩形的性质,解题关键是将动态情况化为某一状态情况,并以这一状态为等量关系建立方程求解.7.：在MBC中,AB = AC,ZBAC = 90° ,尸Q为过点4的一条直线,分别过B、C两点作8M_LP0,CN_L尸.,垂足分别为M、N.(1)如图①所示,当P.与BC边有交点时,求证：MN = CN — BM ；(2)如图②所示,当与6C边不相交时,请写出线段8M、CN和MN之间的数量关系,并说明理由. 【答案】(1)见解析：(2) MN = BM + CN (或BM = MN — CN或CN = MN-BM ),理由见解析【解析】【分析】(1)根据条件先证AAA/i运ACN4,得到AM = CN,BM = AN,即可证得MN = CN — BM： (2)由(1)知AAMBYACNA,得到4M =CN,8M = AN,即可确定MN = BM + CN.【详解】证实：・・・BM_LPQ,CN_LP0,・•. ZAMB=ZCAN=90°,V ZBAC=90 ° ,AZCAN+ZACN=90°,ZCAN+ZBAM=90°(或NCW + NAC/V = NC4N+NMM)・•. ZBAM = ZACN,在AAMB和ACN4中,'ZAMB = 4CNA・.• ZBAM = AACN , AB = CA:.AAM“ACN4(A4S),.・.AM =CN,BM =AN,,: MN = AM-AN,:.MN = CN — BM.(2) MN = BM + CN (或BM=MN-CN或CN = MN-BM) .理由：•.・BM_LPQ,CN_LP.,・•・ ZAMB=ZCAN=90°,V ZBAC=90 ° ,.\ZCAN+ZACN=90°,ZCAN+ZBAM=90°(或NCW + NAC/V = NC4N+NBAM ),:.ZBAM = ZACN,在AAMB和ACNA中,'AAMB = ZCNAZ.B\M = ZACN , AB = CA：.AAM*ACNA( AAS),.・.AM =CN,BM =AN,:.MN = AN + AM = BM+CN.【点睛】此题考察三角形全等的应用,正确确定全等三角形是解题关键,由此得到对应相等的线段,确定它们之间的和差关系得到80、CN和MN之间的关系式.8.操作发现：如图,己知"配和"DE均为等腰三角形,AB=AC, AD=AE,将这两个三角形放置在一起,使点8, D, E在同一直线上,连接CE.(1)如图1, ZABC= ZACB= ZADE= ZAED=55Q,求证：△BADgZkCAE；(2)在(1)的条件下,求N8EC的度数：拓广探索：(3)如图2,假设NC48=NEAD=120.,8D=4, CF为aBCE中8E边上的高,请直接写出讦的长度.【答案】(1)见解析：(2) 70°； (3) 2【解析】【分析】(1)根据SAS证实△BADg/kCAE即可.(2)利用全等三角形的性质解决问题即可.(3)同法可证4BAD丝ZkCAE,推出EC=BD=4,由NBEC=NBAC=12O0,推出NFCE=30°即可解决问题.(1)证实：如图1中,图1Z ABC=^ ACB = Z ADE=N AED, /. Z EAD=Z CAB,：.Z EAC=A DAB,AE=AD. AC=AB9：.△ BAD^ & CAE (SAS).(2)解：如图1中,设AC交8E于O. •「N A8C=N4C8 = 55°,/. Z 84c=180° - 110° = 70°,BAD^△ CAE,Z ABO=Z ECO,Z EOC=ZAOB,・•, Z CEO = Z 840=70°,即 N BEC= 70°.(3)解：如图2中,A图2Z C48 = N EAD=120\•. Z BAD=A CAE,：AB=AC, AD=AE.△ BAD^ 4 CAE 〔SAS〕,•. Z BAD=A ACE. 8D=EC=4,同理可证N BEC- 8AC=120°,Z F£C=60%CFLEF,Z F=90",•. Z FCE=30\1•. EF=-EC=2. 2此题属于三角形综合题,考查了全等三角形的判定和性质等知识,解题的关键是正确寻找全等三角形解决问题,属于中考常考题型.9.在等边aABC中,点.是边8C上一点.作射线AO,点3关于射线AO的对称点为点E.连接CE并延长,交射线AO于点〔1〕如图,连接AE,①AE与AC的数量关系是；②设NBA尸=a,用.表示NBCF的大小；〔2〕如图,用等式表示线段A尸,CF.所之间的数量关系,并证实.【答案】⑴①AB二AE；②NBCF=.：(2)AF-EF=CF,理由见详解.【解析】【分析】(1)①根据轴对称性,即可得到答案；②由釉对称性,得：AE二AB, NBAF=NEAF=.,由△A3C是等边三角形,得AB=AC, ZBAC=ZACB=60° ,再根据等腰三角形的性质和三角形内角和等于180°,即可求解：(2)作NFCG=60°交AD于点G,连接BF,易证AFCG是等边三角形,得GF=FC,再证△ACG会ABCF(SAS),从而得AG=BF,进而可得至lj结论.【详解】(1)①•・•点4关于射线的对称点为点E , AAB和AE关于射线AD的对称,AAB=AE.故答案是:AB=AE;②•.•点3关于射线的对称点为点E , ,AE二AB, NBAF=NEAF=.,•二△A3c是等边三角形,AAB=AC, ZBAC=ZACB=60" ,：.ZEAC=60° -2a, AE=AC,ZACE=1[180 - (60 - 2a)] = 60 +6?,A ZBCF=ZACE-ZACB=60 +a-60°=a .(2) AF-EF=CF,理由如下：作NFCG=60.交AD于点G,连接BF,•••NBAF=NBCF=a , NADB=NCDF,A ZABC=ZAFC=60c ,••.△FCG是等边三角形,AGF=FC,•二△A3c是等边三角形,ABC=AC, ZACB=60° , AZACG=ZBCF=« .在AACG和ABCF中,CA = CBZACG = ABCF , CG = CF,AACG 仝ABCF(SAS),.,.AG=BF,•・•点4关于射线AO的对称点为点E , .\AG=BF=EF,VAF-AG=GF,.\AF-EF=CE【点睛】此题主要考查等边三角形的性质和三角形全等的判定和性质定理,添加辅助线,构造全等三角形,是解题的关键.10.如图,AA8C是等边三角形,点.在边4c上〔“点D不与A,C重合〕,点石是射线5c上的一个动点〔点E不与点8,C重合〕,连接OE,以OE为边作作等边三角形hDEF,连接CF.〔1〕如图1,当.石的延长线与A3的延长线相交,且CF在直线OE的同侧时,过点D 作DG//AB, DG 交BC 于点、G ,求证：CF = EG ；〔2〕如图2,当.石反向延长线与A8的反向延长线相交,且.,尸在直线OE的同侧时,求证：CD = CE+CF；〔3〕如图3,当OE反向延长线与线段A8相交,且.,厂在直线O石的异侧时,猜测CD、CE、CP之间的等量关系,并说明理由.【答案】〔1〕证实见详解；〔2〕证实见详解：〔3〕 CF = CO-CE,理由见详解.【解析】【分析】(1)由AABC 是等边三角形,DG//AB,得NCDG=NA=60° , NACB=60.,ACDG 是等边三角形,易证AGDE仝ACDF(SAS),即可得到结论：(2)过点D作DG〃AB交BC于点G,易证A GDE仝△ CDF(SAS),即可得到结论；(3)过点D作DG〃AB交BC于点G,易证A GDE仝A CDF(SAS),即可得到结论.【详解】(1)•・• AA3C是等边三角形,DG//AB, ：.ZCDG=ZA=60° , ZACB=60° , ・•. ACQG是等边三角形,.\DG=DC.是等边三角形, .,.DE=DF, ZEDF=60° , A ZCDG-ZGDF=ZEDF-ZGDF,即：ZGDE=ZCDF, 在4 GDE和八CDF中,DE = DFNGDE = NCDF ,DG = DC.,.△GDE^A CDF(SAS),：.CF = EG ；(2)过点D作DG〃AB交BC于点G,如图2,•・• AABC是等边三角形,DG//AB、：.ZCDG=ZA=60° , ZACB=60" ,••・ACDG是等边三角形,:.DG=DC.•••ADE/是等边三角形,,DE=DF, ZEDF=60c ,A ZCDG-ZCDE=ZEDF-ZCDE> 即：ZGDE=ZCDF, 在4 GDE和^ CDF中,DE = DFNGDE = ZCDF ,DG = DC.,.△GDE^ACDF(SAS),:・CF = GE,••. CD = CG = CE+GE = CE+CF(3)CF = CD + CE,理由如下：过点D作DG〃AB交BC于点G,如图3,•・・AA8C是等边三角形,DGUAB, .,.ZCDG=ZA=60° , ZACB=60" ,,ACDG是等边三角形, ADG=DC=GC.•・• ADEF是等边三角形, ,DE=DF, ZEDF=60° ,A ZCDG+ZCDE=ZEDF+ZCDE,即：NGDE=NCDF, 在A GDE和4 CDF中,DE = DFNGDE = ZCDF , DG = DCAAGDE^ACDF(SAS),,CF = G£=GC+CE=CD+CE.【点睛】此题主要考查等边三角形的性质和三角形全等的判定和性质定理,添加辅助线,构造全等三角形,是解题的关键.。

第十一章：全等三角形一、基础知识1.全等图形的有关概念 （1）全等图形的定义能够完全重合的两个图形就是全等图形。

例如：图13-1和图13-2就是全等图形图13-1图13-2 （2）全等多边形的定义两个多边形是全等图形，则称为全等多边形。

例如：图13-3和图13-4中的两对多边形就是全等多边形。

图13-3 图13-4（3）全等多边形的对应顶点、对应角、对应边两个全等的多边形，经过运动而重合，相互重合的顶点叫做对应顶点，相互重合的边叫做对应边，相互重合的角叫做对应角。

（4）全等多边形的表示例如：图13-5中的两个五边形是全等的，记作五边形ABCDE ≌五边形A ’B ’C ’D ’E ’（这里符号“≌”表示全等，读作“全等于”）。

图13-5表示图形的全等时，要把对应顶点写在对应的位置。

（5）全等多边形的性质全等多边形的对应边、对应角分别相等。

A B DC E B ’A ’ C ’ D ’ E ’（6）全等多边形的识别多边形相等、对应角相等的两个多边形全等。

2.全等三角形的识别（1）根据定义若两个三角形的边、角分别对应相等，则这两个三角形全等。

（2）根据SSS如果两个三角形的三条边分别对应相等，那么这两个三角形全等。

相似三角形的识别法中有一个与（SSS）全等识别法相类似，即三条边对应成比例的两个三角形相似，而相似比为1时，就成为全等三角形。

（3）根据SAS如果两个三角形有两边机器夹角分别对应相等，那么这两个三角形全等。

相似三角形的识别法中同样有一个是与（SAS）全等识别法相类似，即一角对应相等而夹这个角的两边对应成比例的两个三角形相似，当相似比为1时，即为全等三角形。

（4）根据ASA如果两个三角形的两个角及其夹边分别对应相等，那么这两个三角形全等。

（5）根据AAS如果两个三角形有两个角及其中一角的对边分别对应相等，那么这两个三角形全等。

3.直角三角形全等的识别（1）根据HL如果两个直角三角形的斜边及一条直角边分别对应相等，那么这两个直角三角形全等。

中考数学“全等、相似三角形的存在性问题”题型解析解此类问题，一般分为三个步骤：第一步寻找分类标准；第二步列方程；第三步解方程并验根 .难点在于寻找分类标准，寻找恰当的分类标准，可以使得解的个数不重复不遗漏，也可以使得列方程和解方程又好又快 .一般情况下，寻找一组相等的角或边，分情况列方程 .本节主要来讨论下全等三角形和相似三角形的存在性问题 .类型一：全等三角形存在性问题【例题1】如图，抛物线y = ax^2 + c （a ≠0）与y 轴交于点A，与x 轴交于B , C 两点（点C 在x 轴正半轴上），△ABC 为等腰直角三角形，且面积为4，现将抛物线沿BA 方向平移，平移后的抛物线过点C 时，与x 轴的另一交点为E，其顶点为F，对称轴与x 轴的交点为H .（1）求a , c 的值；（2）连接OF，试判断△OEF 是否为等腰三角形，并说明理由；（3）现将一足够大的三角板的直角顶点Q 放在射线AF 或射线HF 上，一直角边始终过点E，另一直角边与y 轴相交于点P，是否存在这样的点Q，使以点P、Q、E 为顶点的三角形与△POE 全等？若存在，求出点Q 的坐标；若不存在，请说明理由 .【解题策略】（1）关键是利用等腰直角三角形的性质及面积，求出关键点坐标，用待定系数法求解；（2）关键是求得平移后的函数抛物线，证明两边相等即可；（3）关键是分类讨论分两种情形，而情形一又分两种情形，依据全等三角形性质，寻找边角相等求解 .类型二：相似三角形存在性问题【例题2】如图，已知抛物线y = ax^2 + 8/5 x + c 与x 轴交于A , B 两点，与y 轴交于点C，且A（2,0），C（0，-4），直线l : y = -1/2 x - 4 与x 轴交于点D，点P 是抛物线y = ax^2 + 8/5 x + c 上的一动点，过点P 作PE⊥x 轴，垂足为E , 交直线l 于点F .（1）试求该抛物线表达式；（2）如图（1），若点P 在第三象限，四边形PCOF 是平行四边形，求P 点的坐标；（3）如图（2），过点P 作PH⊥y 轴, 垂足为H，连接AC .①求证：△ACD 是直角三角形；②试问当P 点横坐标为何值时，使得以点P , C , H 为顶点的三角形与△ACD 相似？【解题策略】解析本题主要应用了待定系数法求二次函数的解析式、平行四边形的性质、勾股定理的逆定理、相似三角形的性质 .依据平行四边形的对边相等列出关于m 的方程是解析问题（2）的关键；利用相似三角形的性质列出关于n 的方程是解析问题（3）的关键 .。

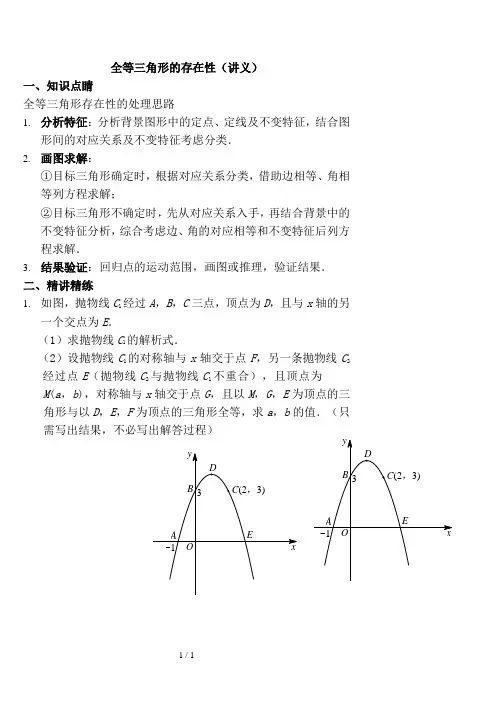
全等三角形的存在性（讲义）一、知识点睛全等三角形存在性的处理思路1.分析特征：分析背景图形中的定点、定线及不变特征，结合图形间的对应关系及不变特征考虑分类．2.画图求解：①目标三角形确定时，根据对应关系分类，借助边相等、角相等列方程求解；②目标三角形不确定时，先从对应关系入手，再结合背景中的不变特征分析，综合考虑边、角的对应相等和不变特征后列方程求解．3.结果验证：回归点的运动范围，画图或推理，验证结果．二、精讲精练1.如图，抛物线C1经过A，B，C三点，顶点为D，且与x轴的另一个交点为E．（1）求抛物线C1的解析式．（2）设抛物线C1的对称轴与x轴交于点F，另一条抛物线C2经过点E（抛物线C2与抛物线C1不重合），且顶点为M(a，b)，对称轴与x轴交于点G，且以M，G，E为顶点的三角形与以D，E，F为顶点的三角形全等，求a，b的值．（只需写出结果，不必写出解答过程）2. 如图，在平面直角坐标系中，抛物线24y ax bx =++与x 轴的一个交点为A (-2，0)，与y 轴的交点为C ，对称轴是直线x =3，对称轴与x 轴交于点B ． （1）求抛物线的函数表达式．（2）若点D 在x 轴上，在抛物线上是否存在点P ，使得 △PBD ≌△PBC ？若存在，直接写出点P 的坐标；若不存在，请说明理由．3. 如图，在平面直角坐标系xOy 中，抛物线2y ax bx c =++与y 轴交于点C (0，4)，对称轴直线2x =与x 轴交于点D ，顶点为M且DM =OC +OD ．（1）求该抛物线的解析式．（2）设点P (x ，y )是第一象限内该抛物线上的一动点，△PCD 的面积为S ，求S与x 之间的函数关系式，并写出自变量x 的取值范围．（3）设点Q 是y 轴右侧该抛物线上的一动点，若经过点Q 的直线QE 与y 轴交于点E ，是否存在以O ，Q ，E 为顶点的三角形与△OQD 全等？若存在，求出直线QE 的解析式；请说明理由．4. 如图，在平面直角坐标系中，直线1l 过点A (1，0)且与y 轴平行，直线2l 过点B (0，2)且与x 轴平行，直线1l 与2l 相交于点P ．点E 为直线2l 上一点，反比例函数k y x=（0k >）的图象过点E 且与直线1l 相交于点F ．（1）若点E 与点P 重合，求k 的值．（2）连接OE ，OF ，EF ．若2k >，且△OEF 的面积为△PEF 面积的2倍，求点E 的坐标．（3）是否存在点E 及y 轴上的点M ，使得以M ，E ，F 为顶点的三角形与△PEF 全等？若存在，求出点E 的坐标；若不存在，请说明理由．【参考答案】 1. （1）223y x x =-++（2）a =7，b =2或a =7，b =-2或a =-1，b =2或a =-1，b =-2或a =1，b =-4或a =5，b =-4或a =5，b =42. （1）213442y x x =-++（2）(18(18--+---，，(4(4+， 3.（1）21242y x x =-++（2）214(022S x x x =-+<<+（3）122y x =+，y =6或724y x =- 4.（1）2 （2）（3，2）（3）3(2)8，，8(2)3，学生做题前请先回答以下问题问题1：全等三角形的判定有哪些？问题2：全等三角形存在性问题中如何确定分类标准，分类标准确定的依据是什么？问题3：全等三角形存在性问题的处理思路是什么？问题4：全等三角形存在性问题与相似三角形存在性问题处理时的异同有哪些？全等三角形的存在性（一）1.如图1，直线y=-2x+4与x轴、y轴分别交于点A，B，点P(x，y)在直线y=-2x+4上，过点P作AB的垂线，与x轴、y轴分别交于点E，F．若△EOF与△AOB全等，则点P的坐标为( )A. B.C.D.2.如图2，已知点A，B 在抛物线上，且点A在第四象限，点B在第一象限，A，B 两点的横坐标满足方程．连接OB，OA，AB，将线段OB绕点O顺时针旋转90°得到线段OC．若D是坐标平面内一点，且△OAB和△OCD全等，则符合题意的点D的坐标为( )图1 图2A.B.C.D.3.如图3，抛物线经过三点，线段BC与抛物线的对称轴相交于点D．P为该抛物线的顶点，连接PA，AD，DP，线段AD与y轴相交于点E．若Q为平面直角坐标系中的一点，且以Q，C，D为顶点的三角形与△ADP全等，则图3 点Q的坐标为( )A. B.C.D.学生做题前请先回答以下问题问题1：全等三角形的判定有哪些？问题2：全等三角形存在性问题的处理思路是什么？全等三角形的存在性（二）1.如图1已知抛物线与x轴交于A，B两点（点A 在点B的左侧），与y轴交于点C，直线与x轴交于点D．在第一象限内，若直线上存在点P，使得以P，B，D为顶点的三角形与△OBC全等，则点P的坐标为( )A.（4，1），（0，3）B.（4，1），（3，2）或（1，2）C.（4，1），（0，3）或（3，2）D.（4，1），（4，-1），（3，2）或（3，-2）2.如图2，直线与x轴、y轴分别交于A，B两点，C是直线上不与A，B重合的动点．过点C的另一直线CD与y轴相交于点D，若以B，C，D为顶点的三角形与△AOB全等，则点C的坐标为( )A. B.C.D.图1 图23.如图3所示，抛物线的顶点为A，直线与y轴的交点为B ，其中．若Q为抛物线的对称轴直线l上一个动点，在对称轴左侧的抛物线上存在点P，使以P，Q，A为顶点的三角形与△OAB全等，则点P的坐标为( )A.图3 B.C.D.学生做题后建议通过以下问题总结反思问题1：结合试题1分析，如何确定分类标准？问题2：画图求解时需要根据分析得到的不变特征，结合两个三角形全等的判定进行分析，试题1中利用的是哪一个全等三角形的判定？问题3：全等三角形存在性问题与相似三角形存在性问题处理时的异同有哪些？学生做题前请先回答以下问题问题1：在处理全等三角形的存在性问题时首先要分析不变特征，那么如何分析不变特征？问题2：在全等三角形存在性问题处理时，依据不变特征处理的核心依据是什么？问题3：课堂所讲解示范的，一般会用哪个判定？问题4：全等三角形存在性处理时都需要考虑哪些方面？问题5：已经学习了平行四边形，菱形，矩形，正方形，相似三角形以及全等三角形等各种存在性，存在性问题处理的框架是什么？全等三角形的存在性（三）1.如图1，已知抛物线与x轴的交点为A，D （A在D的右侧），与y轴的交点为C，点B与点C关于对称轴对称．点M是抛物线上的一点，使得△CMD≌△CMB，则点M的坐标为( )A. B. C. D.2.如图2，已知抛物线与x轴交于A，B两点（点A在点B的右侧），与y轴交于点C，对称轴与x轴交于点D．M 为抛物线上一点，E是x轴上的一点，使得△DMC≌△DME，则点M 的坐标为( ) 图1图2A.B.C.D.3.如图3，已知抛物线与x轴交于A，B两点，与y轴交于C点．若点E在x轴上，点P是抛物线在第一象限上的图3 点，△APC≌△APE，则点P的坐标为( )A. B. C. D.学生做题后建议通过以下问题总结反思问题1：结合第2题考虑全等三角形存在性问题的处理框架是什么？学生做题前请先回答以下问题问题1：全等三角形的判定有哪些？问题2：全等三角形存在性问题的处理思路是什么？问题3：试题1中如何分析不变特征？问题4：试题1中分析不变特征，确定△OPC≌△POQ利用的是全等三角形的哪一个判定？全等三角形的存在性（四）1.如图1，抛物线与y轴交于点C，P是x轴上一个动点，Q是抛物线上异于点C的一个动点．若△OPC≌△POQ，则点Q 的坐标为( )A. B.C.D.2.如图2，抛物线与y轴交于点A，对称轴与x轴交于点B．D是x轴上的一个动点，P是抛物线上的一个动点，使得△DPB≌△ABP，求点P的坐标．（1）要求点P的坐标有如下考虑：分析可知，需要结合A，D和图2 公共边BP的相对位置进行分类讨论．当A，D在BP的同侧时，以A，D，B，P组成的四边形为_________（填“平行四边形”或“等腰梯形”或“梯形”）；当A，D在BP的异侧时，此时以A，D，B，P组成的四边形为_________（填“平行四边形”或“等腰梯形”或“梯形”）．A.平行四边形，梯形B.梯形，平行四边形C.平行四边形，等腰梯形D.等腰梯形，平行四边形( )（2）（上接第2题）当A，D在BP的异侧时，点P的坐标为A.(6，4）B.C.D.4.如图4，抛物线与x轴交于A（-2，0），B（1，0）两点，与y轴交于点C（0，2），P为抛物线x轴上方的一个动点，Q为y轴负半轴上的一个动点．若△ABP≌△BAQ，则点P的坐标为( )A. B.（-1，2） C. D.条件不足，无法求解图4学生做题前请先回答以下问题问题1：全等三角形存在性问题的处理思路是什么？问题2：已经学习了平行四边形，菱形，矩形，正方形，相似三角形以及全等三角形等各种存在性，存在性问题处理的框架是什么？全等三角形的存在性（五）1.如图1，二次函数的顶点为A，与y轴的交点为B．若⊙M 的圆心为，半径为r，过点A向该圆作切线，切点为N，若△AMN与△ABO全等，则满足题意的m，r的值分别为( )A. B.C.D.2.如图2，已知直线与抛物线相交于A，B两点，且点为抛物线的顶点，点B在x轴上．若P是抛物线的第二象限的图象上的一点，使得△POB与△POC全等，则点P 的坐标为( )A. B.C.D.图1 图23.直角坐标系中，O是坐标原点，D 是过三点的抛物线上的一点（不与点A重合）．若以D，O，C为顶点的三角形与△AOC全等，则点D的坐标为( )A. B. C.D.4.如图4，在平面直角坐标系中，直线l 经过．M为x 轴上的一点且，点P，Q在线段AB上．若以O，P，图4 Q为顶点的三角形与△OMP全等，则点P的坐标为( )A. B. C.D.问题1：结合第2题考虑不变特征是什么？分类标准是什么？问题2：结合第4题考虑不变特征是什么？如何确定分类标准？依据是什么？学生做题前请先回答以下问题问题1：动点问题的处理思路是什么？问题2：动点问题分析运动过程，需要关注四要素是什么？、问题3：全等三角形的判定有哪些？问题4：全等三角形存在性问题的处理思路是什么？全等三角形的存在性（六）1.如图1，在△ABC中，AB=AC=10cm，BC=8cm，D为AB的中点．点P在BC边上以3cm/s的速度由点B向点C运动；同时点Q在AC边上以相同的速度由点C向点A运动，其中一个点到达终点时另一个点也随之停止运动．当△BPD与△CQP全等时，点P运动的时间为( )图1 A. B. C. D.2.如图2，抛物线与x轴交于A，B两点，与y轴交于点C．点P是x轴上一动点，点Q是x轴上方抛物线上的一( )个动点．若△AQC与△AQP全等，则点Q的坐标为3.如图3，在第一象限内作射线OC，与x轴的夹角为30°，在射线OC上取一点A，过点A作AH⊥x轴于点H．在抛物线上取点P，在y轴上取点Q，使得以P，O，Q为顶点的三角形与△AOH全等，则符合条件的点A的坐标为( )图3 A. B.C.D.学生做题后建议通过以下问题总结反思问题1：结合试题1考虑，不变特征是什么？△BPD与△CQP利用的是三角形全等的哪一个判定？问题2：试题2中，如何确定分类标准？。

三角形全等的判定总课题全等三角形总课时数第 13 课时课题三角形全等的判定〔综合探究〕主备人课型新授时间教学目标1．理解三角形全等的判定，并会运用它们解决实际问题．2．经历探索三角形全等的四种判定方法的过程，能进行合情推理． 3．培养良好的几何思维，体会几何学的应用价值．教学重点运用四个判定三角形全等的方法．教学难点正确选择判定三角形全等的方法，充分应用“综合法〞进行表达．教学过程教学内容一、回忆反思【课堂演练】1．△ABC≌△A′B′C′，且∠A=48°，∠B=33°，A′B′=5cm，求∠C•′的度数与AB的长．【教师活动】操作投影仪，组织学生练习，请一位学生上台演示．【学生活动】先独立完成演练1，然后再与同伴交流，踊跃上台演示．解：在△ABC中，∠A+∠B+∠C=180°∴∠C=180°-〔∠A+∠B〕=99°∵△ABC≌△A′B′C′，∠C=∠C′，∴∠C′=99°，∴AB=A′B′=5cm．【评析】表示两个全等三角形时，要把对应顶点的字母写在对应位置上，这时解题就很方便．2．：如图1，在AB、AC上各取一点E、D，使AE=AD，连接BD、CE相交于点O，连接AO，∠1=∠2．求证：∠B=∠C．【思路点拨】要证两个角相等，我们通常用的方法有：〔1〕两直线平行，同位角或内错角相等；〔2〕全等三角形对应角相等；〔3〕等腰三角形两底角相等〔待学〕．根据此题的图形，应考虑去证明三角形全等，由条件，可知AD=AE，∠1=•∠2，AO是公共边，叫△ADO≌△AEO，那么可得到OD=OE，∠AEO=∠ADO，∠EOA=∠DOA，•而要证∠B=∠C可以进一步考查△OBE≌△OCD，而由上可知OE=OD，∠BOE=∠COD〔对顶角〕，∠BEO=∠CDO〔等角的补角相等〕，那么可证得△OBF≌△OCD，事实上，得到∠AEO=∠AOD•之后，又有∠BOE=∠COD，由外角的关系，可得出∠B=∠C，这样更进一步简化了思路．【教师活动】操作投影仪，巡视、启发引导，关注“学困生〞，请学生上台演示，然后评点．图1【学生活动】小组合作交流，共同探讨，然后解答．【媒体使用】投影显示演练题2．【教学形式】分组合作，互相交流．【教师点评】在分析一道题目的条件时，尽量把条件分析透，如上题当证明△ADO≌△AEO之后，可以得到OD=OE，∠AEO=∠ADO，∠EOA=∠DOA，•这些结论虽然在进一步证明中并不一定都用到，但在分析时对图形中的等量及大小关系有了正确认识，有利于进一步思考．证明 在△AEO 与△ADO 中，AE=AD ，∠2=∠1，AO=AO ，∴△AEO ≌△ADO 〔SAS 〕，∴∠AEO=∠ADO ．又∵∠AEO=∠EOB+∠B ，∠AOD=∠DOC+∠C ．又∵∠EOB=∠DOC 〔对应角〕，∴∠B=∠C ．3．如图2，∠BAC=∠DAE ，∠ABD=∠ACE ，BD=CE ．求证：AD=AE ．【思路点拨】欲证相等的两条线段AD 、AE 分别在△ABD 和△ACE 中，由于BD=CE ，•∠ABD=∠ACE ，因此要证明△ABD ≌△ACE ，•那么需证明∠BAD=•∠CAE ，•这由条件∠BAC=∠DAE 容易得到．【教师活动】操作投影仪：引导学生思考问题．【学生活动】分析、寻找证题思路，独立完成演练题3．证明：∵∠BAC=∠DAE∴∠BAC-∠DAC=∠DAE-∠DAC 即∠BAD=∠CAE在△ABD 和△ACE 中，∵BD=CE ，∠ABD=∠ACE ，∠BAD=∠CAE ，∴△ABD ≌△ACE 〔AAS 〕，∴AD=AE ．【媒体使用】投影显示演练题3．【教学形式】讲练结合． 图2二、随堂练习1．如图3，点E 在AB 上，AC=AD ，∠CAB=∠DAB ，△ACE 与△ADE 全等吗？△ACB•与△ADB 呢？请说明理由．[答案：△ACE ≌△ADE ，△ACB ≌△ADB ，根据“SAS 〞．]图32．如图4，仪器ABCD 可以用来平分一个角，其中AB=AD ，BC=DC ，将仪器上的点A 与∠PRQ 的顶点R 重合，调整AB 和AD ，使它们落在角的两边上，沿AC 画一条射线AE ，AE 就是∠PRQ 的平分线，你能说明其中道理吗？ 小明的思考过程如下：AB AD BC DC AC AC =⎧⎪=⎨⎪=⎩→△ABC ≌△ADC →∠QRE=∠PRE你能说出每一步的理由吗？ 图43．如图5，斜拉桥的拉杆AB ，BC 的两端分别是A ，C ，它们到O 的距离相等，•将条件标注在图中，你能说明两条拉杆的长度相等吗？答案：相等，因为△ABO ≌△CBO 〔SAS 〕，从而AB=CB ．三、布置作业图5课后反思[教学反思]学生对展开图通过各种途径有了一些了解，但仍不能把平面与立体很好的结合；在遇到问题时，多数学生不愿意自己探索，都要寻求帮助。

《三角形全等的断定》教学反思《三角形全等的断定》教学反思《三角形全等的断定》教学反思1 本节课探究三角形全等的断定方法一，是后面几种断定方法的根底，也是本章的重点也是难点。

教材看似简单，仔细研究后才发现对学生来说有些困难，处理不好可能难以成功。

备课时发现本节课的难点就是处理从确定一个三角形到得到三角形全等的断定方法这个环节，让学生动手操作和学生互相交流验证很好地解决了问题，圆满地完本钱节课的教学任务。

反思整个过程，我觉得做得较为成功的有以下几个方面：1、教学设计整体化，内容生活化。

在课题的引入方面，让学生动手做、裁剪三角形。

既提问复习了全等三角形的定义，又很好的过渡到确定一个三角形需要哪些条件的问题上来。

把知识不知不觉地表达出来，学得自然新颖。

数学学习来于生活实际，学生学得轻松有趣。

2、把课堂充分地让给了学生。

我和学生做了些课前交流，临上课前我先对他们提了四个要求：认真听讲，积极考虑，大胆尝试，踊跃发言。

其实，这是一个调动学生积极性，同时也是鼓励彼此的过程。

在上课过程中，我尽量不做过多的讲解，通过引导让学生发现问题并通过动手操作、交流讨论来解决问题。

3、在难点的打破上获得了成功。

上这堂课前，我一直担忧学生在得出三角形全等的断定方法上出现理解困难。

课堂上我通过让学生动手制作一个两边长分别为6cm和8cm，并要求互相之间互相比拟发现制作的三角形形状和大小完全一样，即三角形都全等，最后同学们都不约而同地得出了三角形全等的断定方法。

但也有几处是值得考虑和在以后教学中应该改良的地方：〔1〕、在课堂上优等生急着演示、发言，后进生却成了观众和听众。

如何做到面向全体，人人学有所得，也值得我们数学老师来讨论。

〔2〕、课堂学生的操作应努力做到学生自发生成的，而不是老师说"你们比拟下三角形的形状和大小"，应换为自发地比拟更好。

〔3〕、教学细节需进一步改良，教学时应多关注学生，在学习新知后，虽然大局部的学生都掌握了，但有少数后进生仍然是不理解。

专题4.3 全等三角形考点1：全等形和全等三角形性质例1．（1）（2022秋·江苏连云港·八年级校考阶段练习）下列图标中，不是由全等图形组合成的是（）A．B．C．D．（2）（2023秋·浙江台州·八年级统考期末）如图，△ABC≌△DEF，且∠A=55°，∠B=75°，则∠F=______°．（3）（2022秋·湖南岳阳·八年级校考期中）如图，△ABC≌△DEC，点B、C、D在同一直线上，且BD=12，AC=7，则CE长为____________．知识点训练1．（2023秋·河北邢台·八年级统考期末）与下图全等的图形是（）A．B．C．D．2．（2020秋·江苏常州·八年级常州市清潭中学校考期中）找出下列各组图中的全等图形（）A．②和⑥B．②和⑦C．③和④D．⑥和⑦3．（2022秋·福建龙岩·八年级统考期末）如图，△DBC≌△ECB，且BE与CD相交于点A，下列结论错误的是（）A．BE=CD B．AB=ACC．∠D=∠E D．BD=AE4．（2023秋·四川自贡·八年级统考期末）如图所示，△ABC≌△AEF，∠B=∠E，有以下结论：①AC=AE；②EF=BC；③∠EAB=∠FAC；④∠EFA=∠AFC．其中正确的个数是（）5．（河北省唐山市2022-2023学年八年级上学期期末考试数学试题）如图，△ABC≌△DEC，点B，C，D在同一条直线上，且CE=1，CD=3，则BD的长是（）A．1.5B．2C．3.5D．46．（2023秋·四川南充·八年级统考期末）如图，点A，E，C在同一直线上，△ABC≌△DEC，AE=3，CD=8，则BC的长为（）A．3B．5C．8D．117．（2023秋·天津·八年级统考期末）如图，已知△ABC≌△DEF，CD平分∠BCA，DF与BC交于点G．若∠A=26°，∠CGF=83°，则∠E的度数是（）A．34°B．36°C．38°D．40°8．（2022秋·河南许昌·八年级统考期中）如图所示的图案是由全等的图形拼成的，其中AD=0.8，BC=1.6，则AF=（）9．（2022秋·山东菏泽·八年级统考期中）下列说法正确的是（）A．形状相同的两个三角形全等B．三个角都分别相等的两个三角形全等C．完全重合的两个三角形全等D．所有的等边三角形全等10．（2022秋·山东烟台·七年级统考期中）下列说法：①角是轴对称图形；②等腰三角形有三条对称轴；③关于某直线成轴对称的两个三角形全等；④两个全等三角形一定关于某条直线成轴对称．其中正确的个数是（）A．1个B．2个C．3个D．4个11．（2022秋·江苏宿迁·八年级统考期中）如图所示的网格是由9个相同的小正方形拼成的，图形的各个顶点均为格点，则∠1−∠2−∠3的度数为（）．A．30°B．45°C．55°D．60°12．（2023·福建南平·统考一模）如图，在△ABC中，∠BAC=135°，将△ABC绕点C逆时针旋转得到△DEC，点A，B的对应点分别为D，E．当点A、D、E在同一条直线上时，下列结论不正确．．．的是（）A．△ABC≌△DEC B．AE=AB+CDC．AD=√2AC D．AB⊥AE13．（2021秋·陕西商洛·八年级统考期末）在平面直角坐标系内，点O为坐标原点，A(−4,0)，B(0,3)．若在该坐标平面内有一点P（不与点A、B、O重合）为一个顶点的直角三角形与Rt△ABO全等，且这个以点P 为顶点的直角三角形与Rt△ABO有一条公共边，则所有符合条件的三角形个数为（）A．3个B．4个C．6个D．7个14．（2023秋·云南曲靖·八年级统考期末）如图，在平面直角坐标系中，点A的坐标为(3,0)，点B的坐标为(0,6)，点C在x轴上运动（不与点A重合），点D在y轴上运动（不与点B重合），当以点C、O、D为顶点的三角形与△AOB全等时，则点D的坐标为______．15．（2023秋·江苏镇江·八年级统考期末）如图，△AOD≌△BOC，∠A=30°，∠C=50°，∠AOC=150°，则∠COD=______°．16．（2023秋·四川南充·八年级统考期末）如图，△ABC绕点C旋转得到△DEC，点E在边AB上，若∠B=75°，则∠ACD的度数是_________．考点2：全等三角形的判定及应用例2．（1）（2023秋·山东威海·七年级统考期末）为了测量湖的宽度AB，小明同学先从A点走到点O处，再继续向前走相同的距离到达点C（即OC=OA），然后从点C沿与AB平行的方向，走到与点O，B共线的点D处，测量C，D间的距离就是湖的宽度．下列可以判断△OCD≌△OAB的是（）A．SSS B．SSA C．SAS D．ASA（2）（2023秋·黑龙江齐齐哈尔·八年级统考期末）如图，已知∠CAE=∠DAB，AC=AD，请你再添加一个条件：___________，使△ABC≌△AED．（3）（2023秋·江苏徐州·八年级统考期末）根据下列条件，能确定△ABC（存在且唯一）的是（）A．AB=2，BC=3，AC=6B．AC=4，BC=3，∠A=60°C．AB=5，BC=3，∠B=30°D．∠A=45°，∠B=45°，∠C=90°（4）（2023秋·广东汕头·八年级统考期末）如图，在△ABC中，∠ACB=65°，∠BAC=70°，AD⊥BC于点D，BM⊥AC于点M，AD与BM交于点P，则∠BPC=______．例3（2022秋·浙江宁波·八年级校考期末）如图，在Rt△ABC中，AB=BC，∠ABC=90°，BO⊥AC于点O，P是OC的中点，D是BC延长线上一点，满足PB=PD．(1)求证∠1=∠2；(2)探究CD与AP之间的数量关系，并给出证明．例4．（2023秋·黑龙江齐齐哈尔·八年级统考期末）综合与实践【阅读理解】课外兴趣小组活动时，老师提出了如下问题：如图（1），△ABC中，AB=8，AC=6，求BC边上的中线AD的取值范围，经过组内合作交流．小明得到了如下的解决方法：延长AD到点E，使DE=AD请根据小明的方法思考：(1)由已知和作图得到△ADC≌△EDB的理由是（）A．SSS B．SAS C．AAS D．HL(2)求得AD的取值范围是___________．【感悟】解题时，条件中若出现“中点”、“中线”字样，可以考虑倍长中线构造全等三角形，把分散的已知条件和所求证的结论集合到同一个三角形中．【问题解决】(3)如图（2），AD是△ABC的中线，BE交AC于E，交AD于F，且AE=EF．求证：AC=BF．知识点训练1．（2022秋·浙江温州·八年级校考期中）如图，在Rt△ABC中，∠ACB=90∘,∠ABC=25∘，O为斜边中点，将线段OA绕点O逆时针旋转a(0∘<α<90∘)至OP，若CB=CP，则α的值为（）A．80∘B．65∘C．50∘D．40∘2．（2023秋·山东威海·七年级统考期末）如图，△ABC和△BDE都是等边三角形，点A，D，E在同一条直线上，BE=2，CE=4，则AE=（）A．6B．5C．8D．73．（海南省海口市（部分校）2022-2023学年八年级上学期期末检测数学试题（A））如图，直线l1∥l2∥l3，且l1与l2的距离为1，l2与l3的距离为3，等腰直角△ABC的三个顶点A、B、C分别在直线l2、l1、l3上，∠ACB=90°，则△ABC的面积为（）D．25A．10B．12C．2524．（2022秋·黑龙江双鸭山·八年级统考期末）如图所示的网格是由9个相同的小正方形拼成的，图形的各个顶点均为格点，则∠2+∠3的度数为（）A．30°B．45°C．55°D．60°5．（2022秋·安徽黄山·八年级统考期末）如图，已知等边△ABC和等边△BPE，点P在BC的延长线上，EC的延长线交AP于点M，连接BM，有下列结论：①AP=CE；②∠PME=60°；③MB平分∠AME；④AM+MC=BM，其中正确的结论是（）A．①②③B．①②④C．①③④D．①②③④6．（2022秋·山西吕梁·八年级统考期末）如图，点E，F在线段AC上，AE=CF，AD⊥DF，CB⊥BE，要根据“HL”证明Rt△ADF≌Rt△CBE，则还需添加的一个条件是（）A．AF=CE B．∠A=∠C C．AD=CB D．AD∥BC7．（2023·全国·九年级专题练习）如图，点O为△ABC的内心，∠B=60°，BM≠BN，点M，N分别为AB，BC上的点，且OM=ON．甲、乙、丙三人有如下判断：甲：∠MON=120°；乙：四边形OMBN的面积为定值；丙：当MN⊥BC时，△MON的周长有最小值．则下列说法正确的是（）A．只有甲正确B．只有乙错误C．乙、丙都正确D．只有丙错误8．（2023秋·浙江台州·八年级统考期末）如图，AB与CD相交于点O，且OA=OB，添加下列选项中的一个条件，不能判定△AOC和△BOD全等的是（）A．OC=ODB．∠A=∠BC．AC=BDD．AC∥BD9．（2023秋·浙江台州·八年级统考期末）如图，射线OC为∠AOB的平分线，点M，N分别是边OA，OB上的两个定点，且OM<ON，点P在OC上，满足PM=PN的点P的个数有（）A．0个B．1个C．2个D．无数个10．（2023秋·河南新乡·八年级统考期末）在△ABC和△DEF中，已知AB=DE，∠A=∠D，下列条件：①AC= DF；②∠B=∠E；③∠C=∠F；④BC=EF．其中一定能判定△ABC≌△DEF的个数为（）A．1B．2C．3D．411．（2022秋·四川广安·八年级统考期末）如图，AB=DC，若要用“SSS”证明△ABC≌△DCB，需要补充一个条件，这个条件是__________．12．（2022秋·福建莆田·八年级统考期末）数学社团活动课上，甲乙两位同学玩数学游戏．游戏规则是：两人轮流对△ABC及△A′B′C′的对应边或对应角添加一组等量条件（点A′，B′，C′分别是点A，B，C的对应点），某轮添加条件后，若能判定△ABC与△A′B′C′全等，则当轮添加条件者失败，另一人获胜．1甲AB=A′B′=2cm2乙∠A=∠A′=35°3甲…上表记录了两人游戏的部分过程，则下列说法正确的是___________．（填写所有正确结论的序号）①若第3轮甲添加∠C=∠C′=45°，则甲获胜；②若第3轮甲添加BC=B′C′=3cm，则甲必胜；③若第2轮乙添加条件修改为∠A=∠A′=90°，则乙必胜；④若第2轮乙添加条件修改为BC=B′C′=3cm，则此游戏最多4轮必分胜负．13．（2023秋·山东淄博·七年级统考期末）如图，点C，E，B，F在同一条直线上，AB=DE，AC=DF，BF=CE．说明AC∥DF．14．（2023秋·江苏南京·八年级统考期末）如图AB=AD,CB=CD,AC,BD相交于点E．(1)求证△ABC≅△ADC；(2)求证BE=DE．15．（2022秋·山西吕梁·八年级统考期末）如图，△ABC是等边三角形，点D，E分别在BC，CA的延长线上，且CD=AE．求证：∠D=∠E．16．（2023秋·广东汕头·八年级统考期末）如图，已知点O在等边△ABC的内部，∠AOB=105°，∠BOC=α，以OC为边作等边△COD，连接AD．(1)求证：AD=BO；(2)当α=150∘时，试判断△AOD的形状，并说明理由；17．（2023秋·江苏南京·八年级统考期末）如图，在四边形ABCD中，连接BD，AB∥CD，且AB=CD．(1)求证：△ABD≅△CDB；(2)若AB=BD，∠ABD=48°，求∠C的度数．18．（2023秋·浙江宁波·八年级校考期末）如图，在四边形ABCD中，P为CD边上的一点，BC∥AD．AP、BP 分别是∠BAD、∠ABC的角平分线．(1)若∠BAD=70°，则∠ABP的度数为_______，∠APB的度数为____________；(2)求证：AB=BC+AD；(3)设BP=3a，AP=4a，过点P作一条直线，分别与AD，BC所在直线交于点E、F，若AB=EF，直接写出AE的长（用含a的代数式表示）考点3：角平分线性质定理和逆定理例5.（2023秋·广东汕头·八年级统考期末）如图，DE⊥AB于点E，DF⊥AC于点F，若BD=CD,BE=CF．(1)求证：AD 平分∠BAC ；(2)请猜想AB +AC 与AE 之间的数量关系，并给予证明．例6.（2022秋·湖北武汉·八年级校考期末）如图，在△ABC 中，E 是BC 中垂线上一点，EM ⊥AB 于M ，EN ⊥AC 于N ，BM =CN ．求证：AE 平分∠BAC ．知识点训练1．（2022秋·贵州铜仁·九年级统考期中）如图，在平面直角坐标系中，△OAB 的顶点B 的坐标为(6,0)，OC 平分∠AOB 交AB 于点C ，反比例函数y =k x (x >0)的图象经过点A ，C ．若S △AOC :S △BOC =2:3，则k 的值为（ ）A ．5√716B ．45√716C ．454D ．916 2．（2023秋·山东济宁·八年级统考期末）如图，Rt △ABC 中，∠C =90°，∠ABC =60°，以顶点B 为圆心、适当长为半径作弧，在边BC 、BA 上截取BE 、BD ；然后分别以点D 、E 为圆心、以大于DE 的长为半径作弧，两弧在∠CBA 内交于点F ；作射线BF 交AC 于点G ．若AC =6，P 为边AB 上一动点，则GP 的最小值为（ ）A．3B．2C．1D．无法确定3．（2023秋·山东淄博·七年级统考期末）如图，已知AB=AC，∠A=36°，AB的垂直平分线MD交AC于点D，AB于点M，以下结论：①△BCD是等腰三角形；②BD是△ACB的角平分线；③△BCD的周长C△BCD=AC+ BC；④△ADM≌△BCD．正确的有（）A．①③B．①②C．①②③D．③④4．（2023秋·黑龙江牡丹江·八年级统考期末）如图，已知△ABC和△ADE都是等腰直角三角形，∠BAC=∠EAD=90°，BD，CE交于点F，连接AF，下列结论：①BD=CE；②∠AEF=∠ADF；③BD⊥CE；④AF 平分∠CAD；⑤∠AFE=45°，其中结论正确的序号是（）A．①②③④B．①②④⑤C．①③④⑤D．①②③⑤5．（2022秋·福建泉州·八年级统考期末）小明同学在学习了全等三角形的相关知识后发现，只用两把完全相同的长方形直尺就可以作出一个角的平分线．如图：一把直尺压住射线OB，另一把直尺压住射线OA并且与第一把直尺交于点P，小明说：“射线OP就是∠BOA的角平分线．”他这样做的依据是（）A．角的内部到角两边距离相等的点在这个角的平分线上．B．角平分线上的点到角两边的距离相等．C．三角形三个内角的平分线交于同一个点．D．三角形三个内角的平分线的交点到三条边的距离相等．6．（2023秋·河北邢台·八年级统考期末）如图，在△ABC中，∠BAC=60°，角平分线BE，CD相交于点P，若AP=4，AC=6，则S△APC=（）．A．4B．6C．12D．247．（2023秋·江苏泰州·八年级统考期末）已知，如图，△ABC中，∠ABC=48°，∠ACB=84°，点D、E分别在BA、BC延长线上，BP平分∠ABC，CP平分∠ACE，连接AP，则∠PAC的度数为（）A．45°B．48°C．60°D．66°8．（2023秋·河北沧州·八年级统考期末）如图，在△AOB和△COD中，OA=OB,OC=OD,OA<OC,∠AOB=∠COD=108∘，连接AC，BD交于点M，连接OM．甲、乙、丙三人的说法如下，下列判断正确的是（）甲：AC=BD；乙：∠CMD>∠COD；丙：MO平分∠BMCA．乙错，丙对B．甲和乙都对C．甲对，丙错D．甲错，丙对9．（2023秋·重庆大足·八年级统考期末）如图，△ABC的三边AC、BC、AB的长分别是8、12、16，点O是△ABC三条角平分线的交点，则S△OAB:S△OBC:S△OAC的值为（）A．4:3:2B．5:3:2C．2:3:4D．3:4:510．（2022秋·甘肃庆阳·八年级统考期中）庆阳市是传统的中药材生产区，优越的地理气候条件形成了较独特的资源禀赋，孕育了丰富的中药植物资源和优良品种，素有“天然药库”“中药之乡”的美称．如图，三条公路把A、B、C三个盛产中药材的村庄连成一个三角形区域，此地区决定在这个三角形区域内修建一个中药材批发市场，要使批发市场到三条公路的距离相等，则这个批发市场应建在（）A．三角形的三条中线的交点处B．三角形的三条角平分线的交点处C．三角形的三条高的交点处D．以上位置都不对11．（2022秋·海南海口·八年级校联考期末）如图，在△ABC中，∠A=90°，BD平分∠ABC，BC=12，AD=4，则△DBC的面积为__________．12．（2023·湖南衡阳·校考一模）如图所示，点O在一块直角三角板ABC上（其中∠ABC=30°），OM⊥AB于点M，ON⊥BC于点N，若OM=ON，则∠ABO=_______度．13．（2023秋·湖北省直辖县级单位·八年级统考期末）如图，△ABC与△BDE都为等边三角形，连接AE与CD，延长AE交CD于点F，连接FB．给出下面四个结论：①AE=CD；②∠AFC=60°；③BF平分∠EBD；④FB 平分∠EFD.其中所有正确结论的序号是__________．14．（2023春·浙江金华·八年级浙江省义乌市后宅中学校考阶段练习）已知：OP平分∠MON，点A，B分别在边OM，ON上，且∠OAP+∠OBP=180°．(1)如图1，当∠OAP=90°时，求证：OA=OB；(2)如图2，当∠OAP<90°时，作PC⊥OM于点C．求证：①PA=PB；②请直接写出OA，OB，AC之间的数量关系．15．（2022春·广东茂名·八年级统考期中）如图，在Rt△ABC中，∠A=90°，∠B=30°，CM平分∠ACB交AB 于点M，过点M作MN∥BC交AC于点N，若AN=1，求BC的长．考点4：线段垂直平分线性质定理和逆定理例7. (1)（2023秋·浙江宁波·八年级宁波市第七中学校考期末）如图，△ABC中，AB<AC<BC，如果要使用尺规作图的方法在BC上确定一点P，使PA＋PB=BC，那么符合要求的作图痕迹是（）A．B．C．D．(2)（2023秋·云南曲靖·八年级统考期末）如图，在△ABC中，∠BAC=110°，EF是边AB的垂直平分线，垂足为E，交BC于F．MN是边AC的垂直平分线，垂足为M，交BC于N．连接AF、AN则∠FAN的度数是（）A．70B．55C．40D．30(3)（2022秋·新疆乌鲁木齐·八年级校考期末）电信部门要再S区修建一座手机信号发射塔，按照设计要求，发射塔到两个城镇A，B的距离必须相等，到两条高速公路OC，OD的距离也必须相等，则发射塔应建在（）A．∠COD的平分线上任意某点处B．线段AB的垂直平分线上任意某点处C．∠COD的平分线和线段AB的交点处D．∠COD的平分线和线段AB垂直平分线的交点处例8.（2023春·重庆沙坪坝·八年级重庆南开中学校考开学考试）如图，在△ABC中，EF是AB的垂直平分线，AD⊥BC于点D，且D为CE的中点．(1)求证：BE=AC；(2)若∠C=70°，求∠BAC的度数．知识点训练1．（2022秋·海南海口·八年级校联考期末）如图，在△ABC中，DE垂直平分BC，若AB=6，AC=8，则△ABD 的周长等于（）A．11B．13C．14D．162．（2023秋·河南南阳·八年级统考期末）如图，等腰△ABC的底边BC长为6，面积是24，E为腰AB的垂直平分线MN上一动点．点D为BC的中点，则△BDE的周长的最小值为（）A．6B．8C．10D．113．（2023秋·福建泉州·八年级校联考期末）如图，根据尺规作图的痕迹，计算∠α的度数为（）A．56∘B．68∘C．28∘D．34∘4．（2023秋·山东东营·八年级统考期末）如图，平行四边形ABCD的对角线AC、BD交于点O，DE平分∠ADCAB，连接OE．下列结论：①S▱ABCD=AD⋅BC；②DB平分∠CDE；③AO=交AB于点E，∠BCD=60°，AD=12DE；④OE垂直平分BD．其中正确的个数有（）A．1个B．2个C．3个D．4个5．（2022秋·河北石家庄·八年级统考期末）如图，在△ABC中，AB=AC，尺规作图：（1）分别以B，C为圆心，BC长为半径作弧，两弧交于点D；（2）连接AD，BD，CD，AD与BC交于点E，则下列结论中错误的是（）A．△ABD≌△ACD B．△DBE≌△DCEC．△BCD是等边三角形D．BC垂直平分AD6．（2023秋·黑龙江牡丹江·八年级统考期末）如图，在△ABC中，∠ACB=90°，∠A=75°，DE垂直平分AB，交AB于点D，交BC于点E，若BE=8cm，则AC为______cm．7．（2023秋·重庆万州·八年级统考期末）如图，在△ABC中，边AC的垂直平分线交BC于点D，交AC于点E，连接AD，若AD是∠BAC的角平分线，且AB=AD时，则∠B=___________°．8．（2023秋·山东淄博·七年级统考期末）如图，已知AB是线段CD的垂直平分线，垂足为点F．E是AB上的一点，∠CEF=30°，CF=2．试求△CED的周长．9．（2022秋·山西吕梁·八年级统考期末）如图，在△ABC中，AB=BC，EF是AB的垂直平分线，交AB于点E，交BC于点F．(1)按要求作图：作∠ABC的平分线BD，交AC于点D，交EF于点O，连接OA，OC（尺规作图，保留痕迹，不写作法）；(2)求证：点O在BC的垂直平分线上；(3)若∠CBD=20°，求∠COF的度数．10．（2023秋·黑龙江齐齐哈尔·八年级统考期末）如图，∠AOB=30°，M，N分别是射线OA,OB上的动点，OP平分∠AOB，OP=9，则△PMN的周长的最小值为（）C．6D．27A．9B．9211．（2022秋·山东临沂·八年级校考期末）.如图，电信部门要在S区修建一座电视信号发射塔．按照设计要求，发射塔到两个城镇A，B距离必须相等，到两条高速公路m和n的距离也必须相等．发射塔应修建在什么位置？在图上标出它的位置．（保留作图痕迹）12．（2023·全国·九年级专题练习）如图，∠HAB=30°，点B与点C关于射线AH对称，连接AC．D点为射线AH 上任意一点，连接CD．将线段CD绕点C顺时针旋转60°，得到线段CE，连接BE．(1)求证：直线EB是线段AC的垂直平分线；(2)点D是射线AH上一动点，请你直接写出∠ADC与∠ECA之间的数量关系．13．（2023秋·山西运城·九年级统考期末）综合与实践问题情境：课堂上老师展示了一张直角三角形纸片．请同学们进行折纸活动，已知在Rt△ABC中．∠ACB=90°，点D、F分别是BC、AB上的一点．连接DF．(1)如图1．小红将△BDF 沿直线DF 折叠，点B 恰好落在BC 上点E 处，若S △BDF S 四边形ACEF=17，则DEDC的值______．(2)如图2，小明将△BDF 沿直线DF 折叠，点B 落在AC 上点E 处，若FE ⊥AC ，求证：四边形BDEF 是菱形； (3)如图3．小亮将△BDF 沿直线DF 折叠，点B 落在AC 延长线上点E 处，且EF 平分∠AED ，若AC =3，BC =4，求CE 的长．14．（2023秋·江苏南京·八年级统考期末）（1）如图1，在△ABC 中，∠A =30°，∠C =90°．求证BC =12AB ．①补全证明过程．证明：如图2，取AB 中点D ，连接CD ． ∴BD =AD =12AB ．在△ABC 中，∠C =90°， ∴______； ∴CD =BD ． 又∠A =30°，∴∠B =90°−∠A =60°． ∴△BCD 为______三角形． ∴BC =BD =12AB ．②请用文字概括①所证明的命题：____________．（2）如图3，某市三个城镇中心D，E，F恰好分别位于一个等边三角形的三个顶点处，在三个城镇中心之间铺设通信光缆，以城镇D为出发点设计了三种连接方案：方案1：DE+EF；方案2：DG+EF（G为EF的中点）；方案3：OD+OE+OF（O为△DEF三边的垂直平分线的交点）．①设DE=6，通过计算，比较三种连接方案中铺设的光缆长度的长短；②不计算，比较三种连接方案中铺设的光缆长度的长短，并说明理由．15．（2023秋·河南洛阳·八年级统考期末）我们已经知道线段是轴对称图形，线段的垂直平分线是线段的对称轴，如图1，直线MN是线段AB的垂直平分线，P是MN上任一点，连接PA、PB，将线段AB沿直线MN对称，我们发现PA与PB完全重合，由此即有：线段垂直平分线的性质定理：线段垂直平分线上的点到线段两端的距离相等．解答下列问题：(1)请你结合图形把已知和求证补充完整，并写出证明过程．已知：如图1，MN⊥AB，垂足为点C，______，点P是直线MN上的任意一点．求证：______．(2)证明：如图2，CD是线段AB垂直平分线，则∠CAD与∠CBD有何关系？请说明理由．考点5：全等三角形的综合问题例9.（2023秋·河南南阳·八年级统考期末）如图，在△ABC中，∠ACB=90°，CE⊥AB于点E，AD=AC，AF平分∠CAB交CE于点F，DF的延长线交AC于点G．(1)求证：DF∥BC；(2)若AE=6，CE=8，求线段GF的长．例10.（2022秋·湖北黄冈·八年级统考期末）已知OM是∠AOB的平分线，点P是射线OM上一定点，点C、D分别在射线OA、OB上，连接PC、PD．(1)如图①，当PC⊥OA，PD⊥OB时，则PC与PD的数量关系是___________；(2)如图②，点C、D在射线OA、OB上滑动，且∠AOB=90∘，当PC⊥PD时，PC与PD在（1）中的数量关系还成立吗？请说明理由．(3)在问题（2）中，若OC+OD=6，则四边形ODPC的面积S是否为定值？若是，请求出该定值，若不是，请说明理由．知识点训练1．（2022秋·河南商丘·八年级统考期中）如图，在△ABC中，∠ABC=90°，D,E分别为边AC,BC上一点，连接BD,DE．已知AB=BE,AD=DE．(1)求证：BD平分∠ABC；(2)若∠A=55°，求证：∠CDE=14∠ADB．2．（2023秋·湖北荆州·八年级统考期末）如图，在△ABC中，BC=2AB，D是AC上一点，∠ABD=20°，E 是BD上一点，EA⊥AB，EB=EC．(1)求证：BD平分∠ABC；(2)求∠DEC的度数．3．（2023秋·重庆长寿·九年级统考期末）在图（1）至图（2）中，直线MN与线段AB相交于点O，∠1=∠2=45°．(1)如图（1），若AO=OB，请写出AO与BD的数量关系和位置关系；(2)将图（1）中的MN绕点O顺时针旋转得到图（2），其中AO=OB．求证：AC=BD，AC⊥BD．4．（2023秋·重庆万州·八年级统考期末）小明在物理课上学习了发声物体的振动实验后，对其作了进一步的探究：在一个支架的横杆点O处用一根细绳悬挂一个小球A，小球A可以自由摆动，如图，OA表示小球静止时的位置．当小明用发声物体靠进小球时，小球从OA摆到OB位置，此时过点B作BD⊥OA于点D，当小球摆到OC位置时，OB与OC恰好垂直（图中的A、B、O、C在同一平面上），过点C作CE⊥OA于点E，测得CE=15cm,AD=2cm．(1)试说明OE=BD；(2)求DE的长．5．（2022秋·海南海口·八年级校联考期末）如图1，在△ABC中，∠BAC=90°，AB=AC，AD⊥BC于点D，∠MDN=90°，将∠MDN绕点D顺时针旋转，它的两边分别交AB、AC于点E、F．(1)求证：△BDE≌△ADF；(2)如图2，若DM=DN，连接BM、NA，求证：BM=AN．6．（2023秋·江苏宿迁·八年级统考期末）如图，已知AC平分∠BAF，CE⊥AB于点E，CF⊥AF于点F，且BC= DC．(1)求证：BE=DF；(2)若AB=21，AD=9，求DF的长．7．（2023秋·广西南宁·九年级统考期末）如图，将矩形ABCD绕点B旋转得到矩形BEFG，点E在AD上，延长DA交GF于点H.(1)求证：△ABE≅△FEH；(2)连接BH，若∠EBC=30°，求∠ABH的度数．8．（2023秋·山东威海·七年级统考期末）在四边形ABDE中，点C是BD边的中点．(1)如图①，AC平分∠BAE，∠ACE=90°，写出线段AE，AB，DE间的数量关系及理由；(2)如图②，AC平分∠BAE，EC平分∠AED，∠ACE=120°，写出线段AB，BD，DE，AE间的数量关系及理由．9．（2022秋·广西柳州·八年级统考期末）在平面直角坐标系中，点O为坐标原点，A(a,0)，B(0,b)，且a，b满足(a−3)2+|b−3|=0，连接AB．(1)求点A，B点的坐标；(2)如图1，动点C从点O出发，以1个单位/秒的速度沿y轴正半轴运动，运动时间为t秒(0<t<3)，连接AC，过点C作CD⊥AC，且CD=CA，点D在第一象限，请用含有t的式子表示点D的坐标；(3)在（2）的条件下，如图2，连接并延长DB交x轴于点E，连接AD和AB，过点B作线段BF交x轴于点F，使得∠OBF=∠DCB，已知此时点F的坐标为(−1,0)，求△ADE的面积．10．（2023秋·福建福州·八年级统考期末）在平面直角坐标系xOy中，点A(0,a)，B(b,0)，C(c,0)，点D在第四象限，其中a>0，b<0，c>0，∠BAC+∠BDC=180°，AC⊥CD．(1)如图1，求证：∠BAO=∠CBD；(2)若|a−c|+b2+6b+9=0，且AB=BD．①如图1，求四边形ACDB的面积；（用含a的式子表示）②如图2，BD交y轴于点E，连接AD，当E关于AD的对称点K落在x轴上时，求CK的长．。