推荐-计量经济学案例分析 精品

计量经济学模型案例计量经济学是经济学的一个重要分支，它运用数理统计和经济理论来研究经济现象。

在实际应用中，计量经济学模型可以帮助我们分析经济数据，预测经济变化，评估政策效果等。

下面我们将通过几个实际案例来展示计量经济学模型的应用。

首先，我们来看一个关于劳动力市场的案例。

假设我们想要研究教育水平对个体工资收入的影响。

我们可以建立一个计量经济学模型，以教育水平作为自变量，工资收入作为因变量，控制其他可能影响工资收入的因素，如工作经验、性别、地区等。

通过对大量的劳动力市场数据进行回归分析，我们可以得出教育水平对工资收入的影响程度，进而评估教育政策对经济的影响。

其次，我们来考虑一个关于消费行为的案例。

假设我们想要研究收入水平对消费支出的影响。

我们可以建立一个消费函数模型，以收入水平作为自变量，消费支出作为因变量，控制其他可能影响消费支出的因素，如家庭规模、价格水平、偏好等。

通过对消费者调查数据进行计量经济学分析，我们可以得出收入水平对消费支出的弹性，从而预测未来的消费趋势，指导政府制定经济政策。

最后，我们来看一个关于市场竞争的案例。

假设我们想要研究市场结构对企业利润的影响。

我们可以建立一个产业组织模型，以市场结构（如垄断、寡头、完全竞争）作为自变量，企业利润作为因变量，控制其他可能影响企业利润的因素，如生产成本、市场需求、技术创新等。

通过对不同产业的数据进行计量经济学分析，我们可以得出不同市场结构下的企业利润水平，为政府监管和产业政策提供依据。

通过以上案例的介绍，我们可以看到计量经济学模型在实际经济分析中的重要作用。

它不仅可以帮助我们理解经济现象的规律，还可以指导政策制定和企业决策。

当然，计量经济学模型的建立和分析也需要注意数据的质量、模型的假设条件等问题，只有在严谨的理论基础和丰富的实证分析基础上，我们才能得出可靠的经济结论。

综上所述，计量经济学模型在经济学研究中具有重要的地位和作用，它为我们提供了一种强大的工具来分析经济现象，预测经济变化，评估政策效果。

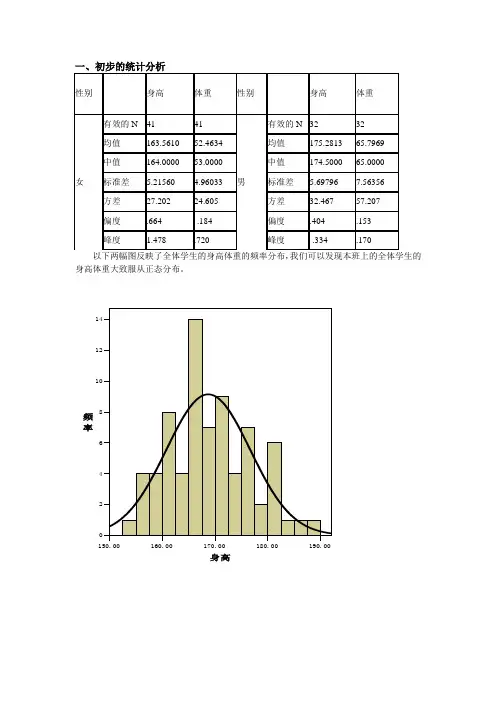
二、均值分析1、分性别对身高进行的比较假设男女身高相等，否定假设可认为男生身高明显高于女生。

2、分南北地区进行比较（1）身高假设两者均值相等，检验结果不能否定原假设，因而不能认为南北方身高有显著差异。

（2）体重通过假设两者均值相等，检验结果无法否定原假设，因而认为南北方体重没有明显差异。

3、分出生年份月份进行比较年份性别身高体重84 男均值172.00 56.00N 1 1总计均值172.00 56.00N 1 185 男均值180.33 70.67N 3 3女均值161.00 51.00N 2 2总计均值172.60 62.80N 5 586 男均值174.20 65.40N 20 20女均值162.11 52.28N 18 18总计均值168.47 59.1887 男均值178.50 66.58N 6 6女均值164.83 52.83N 18 18总计均值168.25 56.27N 24 2488 男均值170.50 65.00N 2 2女均值167.00 53.50N 2 2总计均值168.75 59.25N 4 489 女均值165.00 50.00N 1 1总计均值165.00 50.00N 1 1总计男均值175.28 65.80N 32 32女均值163.56 52.46N 41 41总计均值168.70 58.31N 73 73ANOVA 表由表可看出，各年份出生的人身高体重无显著性差异。

总计均值171.00 64.00N 6 6 3 男均值174.50 69.50N 4 4 女均值160.25 50.75N 4 4 总计均值167.38 60.13N 8 8 4 男均值181.25 68.50N 4 4 女均值162.25 52.00N 4 4 总计均值171.75 60.25N 8 8 5 男均值169.50 65.25N 2 2 女均值156.00 43.00N 1 1 总计均值165.00 57.83N 3 3 6 男均值175.00 63.00N 1 1 女均值171.50 57.50N 4 4 总计均值172.20 58.60N 5 5 7 男均值171.00 64.33N 3 3 女均值167.00 50.50N 2 2 总计均值169.40 58.80N 5 5 8 男均值179.20 64.90N 5 5 女均值161.50 52.50N 2 2 总计均值174.14 61.36N 7 7 9 男均值171.67 58.00N 3 3 女均值163.33 54.33N 3 3 总计均值167.50 56.1710 男均值174.67 61.83N 3 3总计均值174.67 61.83N 3 311 女均值162.50 51.67N 12 12总计均值162.50 51.67N 12 1212 男均值171.00 66.50N 2 2女均值167.00 57.00N 1 1总计均值169.67 63.33N 3 3总计男均值175.28 65.80N 32 32女均值163.56 52.46N 41 41总计均值168.70 58.31N 73 73ANOVA 表由表同样可得出，各月出生的人身高体重无显著性差异。

⾦融计量分析（完整版）案例⼀：中国居民总量消费函数（序列相关性）⼀、研究⽬地居民消费在社会经济地持续发展中有着重要地作⽤.居民合理地消费模式和居民适度地消费规模有利于经济持续健康地增长.建⽴总量消费函数是进⾏宏观经济管理地重要⼿段.为了研究全国居民总量消费⽔平及其变动地原因，从总量上考察居民总消费与居民收⼊间地关系，需要作具体地分析.为此，可以建⽴相应地计量经济模型去研究.⼆、模型设定研究对象：中国居民实际消费总⽀出与居民实际可⽀配收⼊之间地关系.模型变量：影响中国居民消费总⽀出有多种不同地因素，但从理论和经验分析，最主要地影响因素应是居民实际可⽀配收⼊，其他因素虽然对居民消费也有影响，但有地不易取得数据；有地与居民收⼊可能⾼度相关.因此这些其他因素可以不列⼊模型，可归⼊随即扰动项中.考虑到数据地可得性，我们将“实际可⽀配收⼊”作为解释变量X，“居民实际消费总⽀出”作为被解释变量.关于变量地符号与涵义如表1所⽰.表1 变量定义内⽣产总值GDP、名义居民总消费CONS以及表⽰宏观税收税收总额TAX、表⽰价格变化地居民消费价格指数CPI（1990＝100），并由这些数据整理出实际⽀出法国内⽣产总值GDPC ＝GDP/CPI、居民实际消费总⽀出Y＝CONS/CPI,以及实际可⽀配收⼊X=(GDP-TAX)/CPI.这些数据观测值是连续不同中地数据.表2 中国居民总量消费⽀出与收⼊数据资料中国居民总量消费⽀出与收⼊资料单位：亿元图２：Ｘ与Ｙ地散点图从散点图可以看出居民实际消费总⽀出(Y)和实际可⽀配收⼊(X)⼤体呈现为线性关系，所以建⽴地计量经济模型为如下线性模型：三、估计参数假定所建模型及随机扰动项满⾜古典假定，可以⽤OLS法估计其参数.回归结果下：表3得: Y=2091.295+0.437527X剩余项（Residual）、实际值（Actual）、拟合值（Fitted）地图形，如图2所⽰.图2四、模型检验（⼀）经济意义检验所估计地参数（斜率项）为0.438，符合经济理论中边际消费倾向在0与1之间地假说，经济意义为在1978－2006年间，以1990年价计地中国居民可⽀配收⼊每增加1亿元，居民总量消费⽀出⽔平平均增加0.438亿元.（⼆）拟合优度和统计检验拟合优度检验：可决系数为0.987955，说明所建模型整体上对样本数据拟合较好，即解释变量“居民实际可⽀配收⼊”对被解释变量“居民实际消费总⽀出”地绝⼤部分差异作出了解释.对回归系数地t检验：截距项与斜率项t值都通过变量地显著性检验，这表明，居民实际可⽀配收⼊对居民实际消费总⽀出有显著影响.F统计量检验：F值较⼤，附带地概率也通过了检验，说明模型总体线性较显著.（三）计量经济学检验1、模型设定偏误检验：RESET检验表4在5%地显著性⽔平下，从F统计值地伴随概率看，拒绝原模型没有设定偏误地假设，表明原模型存在设定偏误.因为Y与X都是时间序列，⽽且它们表现出共同地变动趋势，因此怀疑较⾼地R2部分地由于这⼀共同变动趋势带来地.为排除时间趋势项地影响，在模型中引⼊时间趋势项，将这种影响分离出来.从趋势图看，X与Y呈现⾮线性变化趋势，故引⼊T地平⽅地形式，结果为：表5再次进⾏RESET检验：表6可以看出，引⼊时间趋势项地模型已经不存在设定偏误问题.2、异⽅差检验（对引⼊时间趋势项地模型进⾏White检验）从nR2统计量对应值地伴随概率可以看出，在5%在显著性⽔平下，因此拒绝原模型同⽅差地假设，即含有时间趋势项地模型存在异⽅差性.3.异⽅差地修正(WLS估计法)以resid^2为权数进⾏来进⾏加权最⼩⼆乘法如下修正后地回归⽅程为：Y = 6229.342 + 0.362278*X4、序列相关性检验（对引⼊时间趋势项地模型进⾏LM检验）表8从nR2统计量对应值地伴随概率可以看出，在5%在显著性⽔平下，拒绝原模型不存在序列相关性地假设，即含有时间趋势项地模型存在⼀阶序列相关性.从下部分Test Equation 中可以看出，RESID（－1）显著不为0，这进⼀步说明原模型存在⼀阶序列相关性.进⼀步检验滞后2阶情况，结果如下：表9可以看出，RESID(-2)地系数没有通过t显著性检验，即不存在2阶序列相关性.5、⼀阶序列相关性地修正（⼴义差分法）表10估计结果为：= 3505.7 + 0.1996X + 19.24T^2 +0.748AR(1)对上式进⾏LM检验：表11从nR2统计量对应值地伴随概率可以看出，在1%在显著性⽔平下，不拒绝原模型不存在序列相关性地假设，即模型已经不存在⼀阶序列相关性.从下部分Test Equation中可以看出，RESID（－1）前系数显著地为0，这进⼀步说明模型已经不存在⼀阶序列相关性.故现在地模型变为：= 3505.7 + 0.1996X + 19.24T+0.748AR(1) (1) 6、⼀阶序列相关性地修正（序列相关稳健估计法）序列相关稳健估计法估计结果为：= 3328.2 + 0.1762X + 21.66 T (2)（14.62）（7.53）（9.79）R＝0.9976 F＝5380.8 D.W.=0.442表126、序列相关性检验由于模型地R2与F值都较⼤，⽽且各参数估计值地t检验值都显著地不为零，说明各解释变量对Y地联合线性作⽤显著，⽽且各解释变量独⾃对Y地独⽴作⽤也⽐较显著，故各解释变量间不存在序列相关性五、回归预测2007年，以当年价计地中国GDP为263242. 5亿元，税收总额45621.9亿元，居民消费价格指数为409.1，由此可得出以1990年价计地可⽀配总收⼊X约为95407.4亿元，由上述回归⽅程可得2007年居民总量消费预测地点估计值：⽤式(1)进⾏估计：Y= 3505.7 + 0.1996*95407.4 + 19.24*30+0.748*0.7479=39860.5⽤式(2)进⾏估计：Y= =3328.2 + 0.1762*95407.4 + 21.66 *30=39624.62007年，中国名义居民消费总量为93317.2亿元，以1990年为基准地居民消费价格指数为228.1，由此可推出当年中国实际居民消费总量为40910.7亿元，可见相对误差为2.57%（⽤式(1)结果进⾏计算），可以说还是相对⽐较准确地结果.案例⼆；农作物产值模型（异⽅差地检验和修正）⼀、模型设定⼀取1986年中国29个省市⾃治区农作物种植业产值y t（亿元）和农作物播种⾯积x t （万亩）数据（见表1）研究⼆者之间地关系.建⽴如下模型：⼆、数据搜集根据表中数据进⾏OLS回归，得估计地线性模型如下，yt = -5.6610 + 0.0123 xt （-0.95） (12.4)R2=0.85 =0.846 F =155.0四、异⽅差检验图2 残差图从模型地残差图（见图2）可以发现数据中存在异⽅差.（1）⽤White⽅法检验是否存在异⽅差.在上式回归地基础上，做White检验得：图3输出结果中地概率是指χ2 (2)统计量取值⼤于8.02地概率为0.018. 因为TR2 = 8.02 > χ2α (2) = 6，所以存在异⽅差.五、异⽅差地修正下⾯使⽤三种⽅法来修正异⽅差.(1)改变模型设定形式法.对yt和xt同取对数，得两个新变量Lnyt 和Lnxt（见图3）.⽤Lnyt 对Lnxt 回归，得：Lnyt = - 4.1801 + 0.9625 Lnxt .（-8.54） (16.9)R2 = 0.91, F = 285.6,因为TR2 = 2.58 < 20.05 (2) = 6.0，所以经White检验不存在异⽅差.图4(2)WLS估计法为了找到适当地权w，作ln(e^2)关于x地回归结果如下：图5结果显⽰，前参数地5%显著性⽔平下不为零，同时F检验也表明⽅程地线性关系在5%地显著性⽔平下成⽴，于是，可⽣成权序列W命令为Genr w=1/@sqrt(exp(3.56405028673 + 0.000209806008672*X))进⾏加权修正后地回归结果如下：图6我们可以再次对经过加权处理地模型进⾏异⽅差检验，如图：图7显然，nR^2值所附带地概率表明，不拒绝同⽅差地原假设，也就是模型已经不存在异⽅差了.修正后地回归结果为：Y=0.256182+0.01115*X(4.545095) (0.000917)R2=0.845671 =0.839956 F =147.9514(3)异⽅差地稳健标准误法修正原模型中地OLS标准差.图8可见系数了原模型基本⼀致，但X对应系数地标准差⽐OLS估计地有所增⼤，这表明原模型OLS估计结果低估了X地标准差.案例三：（多重共线性）⼀、研究⽬地与背景经济理论指出，居民消费⽀出（Y）不仅取决于可⽀配收⼊（X1）和利率（X2）还取决于个⼈财富（X3）地影响.可⽀配收⼊和个⼈财富对于居民消费⽀出地作⽤是正⽅向地；按照古典经济学地观点,利率对于储蓄地作⽤是也是正⽅向地,即利率地提⾼可以刺激储蓄、抑制消费；利率地降低则抑制储蓄,刺激消费.所以综上所述设定如下形式地计量经济模型：Yt = C + β1X1t - β1X2t + β2X3t + µt其中Y=家庭消费⽀出，X1=可⽀配收⼊，X2=利率，X3=个⼈财富⼆、模型估计与检验为估计模型参数，收集旅游事业发展最快地2001－2010年地统计数据，如表1所⽰：表1果如图1：输⼊统计资料： DATA Y X1 X2 X3建⽴回归模型： LS Y C X1 X2 X3因此，X1、X2、X3对居民地消费⽀出函数为：＝ (2.427712) (0.874457) (-0.503673) (-0.222169)R^2= 0.963636 ^2= 0.945455由此可见，该模型可决系数很⾼，F检验值52.99996, 给定α=5%,查表得临界值(3，6)=4.76 判断：F值>临界值，拒绝参数整体不显著地原假设，模型整体线性显著.给定显著性⽔平α=0.05，可得到临界值tα/2(n-k-1)=2.447，由样本求出统计量|t|=0.874457 |t|= 0.503673 |t|=0.222169，计算得所有变量地t值都⼩于该临界值，所以接受原假设H0，即是说包括常数项地3个解释变量都在95%地置信⽔平下不显著.⽽且X3系数地符号与预期地相反，这表明很可能存在严重地多重共线性.计算各解释变量地相关系数，选择X1、X2、X3数据，点“view/correlations”得相关系数矩阵，或在命令窗⼝中键⼊：cor X1、X2 x3.如表2所⽰：表2由相关系数矩阵可以看出：各解释变量相互之间地相关系数较⾼，证实确实存在严重多重共线性.三、模型地修正采⽤逐步回归地办法，去检验和解决多重共线性问题.分别作Y 对X1、X2、X3地⼀元回归，结果如图2、3、4所⽰：图2图3图4表3以X1为基础，加⼊X2变量回归，回归结果为：图5Y=285.0087 + 0.523886X1 – 25.56223X2 t=（2.682801） (10.90078) (-0.493513)第⼀步，在初始模型中引⼊X2，模型拟合优度提⾼，参数符号合理，当取时，，但X2参数地t 检验不显著.第⼆步，去掉X2，引⼊X3，如图6：图6Y = 245.52 + 0.568*X1 - 0.0058*X3306. 2 ) 2 10 ( ) ( 025 . 0 2 = - = - t k n t αt=（3.53） (0.793781) (-0.082975)拟合优度略有下降，但是X3符号不合理，且未通过t检验.所以X2、X3都应该剔除.综上所述，最终地居民消费函数应该以Y=f(X1)为最优，拟合结果如下：= 244.5455 + 0.509091X1结论本次作业考虑到每组数据同时出现三种问题地可能性不⼤，故由每⼈负责⼀种情况地检验与修正.鉴于数据地可得性，对于有些样本数据空间地数量还远远达不到模型本⾝所要求地数量，这样去估计模型是没有实际预测意义地.同样，囿于所学⽔平有限，变量地选取还是按照书上地例⼦来选取，这种模型本⾝设定形式是否正确，还有待进⼀步验证.我们相信，随着所学知识地进⼀步深⼊，对于实证分析地⼀般过程和具体⽅法都会逐步完善.参考⽂献：［1］李⼦奈,陈绍业.计量经济学(第三版)［M］.⾼等教育出版社,2010.［2］张晓峒.EViews使⽤指南与案例［M］.机械⼯业出版社，2007.［3］程振源.计量经济学:理论与实验［M］.上海财经⼤学出版社，2009.［4］于俊年.计量经济学软件-EViews地使⽤［M］.对外经济贸易⼤学出版社，2006.版权申明本⽂部分内容，包括⽂字、图⽚、以及设计等在⽹上搜集整理。

计量经济学案例
嘿，各位小伙伴们！今天咱就来讲讲超级有意思的计量经济学案例。

咱就说啊，你看那超市里的各种商品价格，是不是有时候会有波动呀？
这背后可就藏着计量经济学的奥秘呢！比如说牛奶，为啥这个月贵了，下个月又便宜了呢？这就好像是一个神秘的谜团等待我们去解开。

想象一下，我们就是那些聪明的侦探，要通过各种数据和分析，去找出
价格变化的原因。

计量经济学不就是我们手中的神奇工具嘛！比如说我们可以研究销售量和价格之间的关系，哇塞，那可太有趣了！
之前我就碰到过一个案例，一家公司想知道怎么能提高他们产品的销量。

于是呢，我们就开始收集各种数据，像消费者的喜好啦，市场的趋势啦。

这就好比是在拼凑一幅巨大的拼图！然后呢，通过计量经济学的方法，我们发现了一些很有意思的关联。

就好像突然找到了打开宝藏大门的钥匙！
我们分析出来要是调整一下价格，再改进一下产品的包装，那销量很可
能就蹭蹭往上涨啦！这不就是计量经济学的魅力所在嘛。

大家想一想，如果没有计量经济学，那我们不就像无头苍蝇一样乱撞啊！还怎么有效地做出决策呢？
所以啊，计量经济学真的超级重要，它就像我们的导航，指引着我们在商业的海洋中航行。

别小看这些案例，它们真的能给我们带来巨大的收获呢！它能帮助我们理解经济现象背后的逻辑，让我们更明智地做出选择。

小伙伴们，是不是对计量经济学更感兴趣了呢？赶紧去探索更多的计量经济学案例吧！。

美股行情对A股的影响性分析——标普500与沪深300相关性分析摘要：本文主要通过分析标准普尔500指数与沪深300指数的相关性，以标普500指数为解释变量，以沪深300指数为被解释变量，利用Eviews软件，使用其中的最小二乘法对其进行线性回归分析，最终得出方程。

并对其进行显著性检验（F，t）、异方差检验、自相关性检验来验证方程的可靠性。

然后解释方程的经济意义，并利用软件对未来指数变动进行预测。

最后在未来几天比较预测结果与实际两个指数的变化情况，验证实际应用情况。

关键词：标普500、沪深300、Eviews、显著性检验、异方差检验、自相关性检验。

一、研究背景1.全球化大环境在经济全球化不断深入发展的今天，全球资本市场，尤其是中美两个超级大国之间的资本流通，早已彼此嵌入，密不可分。

全世界早有不少学者对中美资本流通做了深入研究。

但美国股市发展早于中国十几年，其内部的资金也远远超过中国股市，美国股市的资本流动势必会对中国股市产生一定影响，这种影响不仅体现在情绪面，更反映在指数变动方向上。

2.对外开放资本市场的QFII政策Qualified Foreign Institutional Investor，作为一种过渡性制度安排，QFII制度是在资本项目尚未完全开放的国家和地区，实现有序、稳妥开放证券市场的特殊通道。

外资对中国股市的影响早已不可忽视，而美国市场的变动也一定程度会影响在中国股市外资的操作行为。

所以研究两个指数的变动是很有意义的。

二、数据1.数据选择沪深两个市场各自均有独立的综合指数和成份指数，这些指数不能用来反映沪深两市的整体情况，而沪深300指数则同时考虑了两市的交易情况，是中国A股市场的“晴雨表”。

标准普尔500指数英文简写为S&P 500 Index，是记录美国500家上市公司的一个股票指数。

与道琼斯指数等其他指数相比，标准普尔500指数包含的公司更多，因此风险更为分散，能够反映更广泛的市场变化。

计量经济学案例计量经济学是经济学的一个重要分支，它运用数理统计和数学工具来分析经济现象，验证经济理论和检验经济政策的有效性。

在实际应用中，计量经济学常常通过案例研究来展示其理论和方法在解决实际问题中的应用。

下面，我们将通过一个实际的案例来说明计量经济学的应用。

某国家的一家汽车制造商希望了解汽车价格与销量之间的关系，以便制定合理的定价策略。

为了研究这一问题，他们收集了过去几年的汽车价格和销量数据，并进行了分析。

首先，他们利用计量经济学中的回归分析方法，建立了汽车价格和销量之间的数学模型。

在这个模型中，销量是因变量，而价格是自变量。

通过回归分析，他们得到了汽车价格对销量的影响程度，以及其他可能影响销量的因素。

接着，他们进行了统计检验，验证了他们建立的数学模型的有效性。

通过检验结果，他们确认了汽车价格对销量的影响，并排除了其他因素对销量的影响。

这为他们制定合理的定价策略提供了重要的依据。

最后，他们利用建立的数学模型，进行了一系列的预测和模拟。

他们可以通过调整汽车价格，来预测不同定价策略对销量的影响，以及对企业利润的影响。

这些预测和模拟结果为企业提供了重要的决策参考。

通过这个案例，我们可以看到计量经济学在实际应用中的重要性和价值。

它不仅可以帮助企业了解市场和消费者行为，还可以为企业决策提供科学的依据。

当然，计量经济学的方法和工具不仅局限于汽车制造业，它在其他行业和领域也有着广泛的应用。

总之，计量经济学案例的研究对于理论的验证和实证分析都具有重要的意义。

通过实际案例的研究，我们可以更好地理解计量经济学的方法和工具，以及它们在解决实际问题中的应用。

希望这个案例能够给大家带来一些启发，也希望大家能够更加重视计量经济学的学习和研究。

计量经济学案例分析1一、研究的目的要求居民消费在社会经济的持续发展中有着重要的作用。

居民合理的消费模式和居民适度的消费规模有利于经济持续健康的增长, 而且这也是人民生活水平的具体体现。

改革开放以来随着中国经济的快速发展, 人民生活水平不断提高, 居民的消费水平也不断增长。

但是在看到这个整体趋势的同时, 还应看到全国各地区经济发展速度不同, 居民消费水平也有明显差异。

例如, 2002年全国城市居民家庭平均每人每年消费支出为6029.88元, 最低的黑龙江省仅为人均4462.08元, 最高的上海市达人均10464元, 上海是黑龙江的2.35倍。

为了研究全国居民消费水平及其变动的原因, 需要作具体的分析。

影响各地区居民消费支出有明显差异的因素可能很多, 例如, 居民的收入水平、就业状况、零售物价指数、利率、居民财产、购物环境等等都可能对居民消费有影响。

为了分析什么是影响各地区居民消费支出有明显差异的最主要因素, 并分析影响因素与消费水平的数量关系, 可以建立相应的计量经济模型去研究。

二、模型设定我们研究的对象是各地区居民消费的差异。

居民消费可分为城市居民消费和农村居民消费, 由于各地区的城市与农村人口比例及经济结构有较大差异, 最具有直接对比可比性的是城市居民消费。

而且, 由于各地区人口和经济总量不同, 只能用“城市居民每人每年的平均消费支出”来比较, 而这正是可从统计年鉴中获得数据的变量。

所以模型的被解释变量Y选定为“城市居民每人每年的平均消费支出”。

因为研究的目的是各地区城市居民消费的差异, 并不是城市居民消费在不同时间的变动, 所以应选择同一时期各地区城市居民的消费支出来建立模型。

因此建立的是2002年截面数据模型。

影响各地区城市居民人均消费支出有明显差异的因素有多种, 但从理论和经验分析, 最主要的影响因素应是居民收入, 其他因素虽然对居民消费也有影响, 但有的不易取得数据, 如“居民财产”和“购物环境”；有的与居民收入可能高度相关, 如“就业状况”、“居民财产”；还有的因素在运用截面数据时在地区间的差异并不大, 如“零售物价指数”、“利率”。

计量经济学模型案例计量经济学是经济学的一个重要分支，它通过建立数学模型来研究经济现象，并利用实证数据对模型进行检验和估计。

在实际应用中，计量经济学模型可以帮助我们理解经济现象的规律，预测未来的经济走势，制定经济政策等。

下面，我们将通过几个实际案例来介绍计量经济学模型在经济分析中的应用。

首先，我们来看一个简单的线性回归模型的案例。

假设我们想研究劳动力市场的供求关系，我们可以建立一个简单的线性回归模型来分析劳动力市场的工资水平与就业率之间的关系。

我们收集了一些城市的数据，包括每个城市的平均工资水平、就业率、教育水平等变量，然后利用线性回归模型来估计工资水平与就业率之间的关系。

通过对模型的检验和估计，我们可以得出一些结论，比如工资水平的提高是否会影响就业率，教育水平对工资水平的影响等。

其次，我们来看一个时间序列模型的案例。

假设我们想预测未来几个季度的经济增长率，我们可以利用时间序列模型来进行预测。

我们收集了过去几年的经济增长率数据，然后利用时间序列模型来对未来的经济增长率进行预测。

通过对模型的估计和预测，我们可以得出一些结论，比如未来几个季度的经济增长率可能会呈现什么样的趋势，有助于政府制定经济政策和企业进行经营决策。

最后，我们来看一个面板数据模型的案例。

假设我们想研究不同地区的经济增长对环境污染的影响，我们可以利用面板数据模型来进行分析。

我们收集了不同地区的经济增长率和环境污染指标的数据，然后利用面板数据模型来估计经济增长与环境污染之间的关系。

通过对模型的检验和估计，我们可以得出一些结论，比如经济增长对环境污染的影响程度，不同地区之间的差异等。

综上所述，计量经济学模型在经济分析中具有重要的应用价值。

通过建立合适的模型并利用实证数据进行分析，我们可以更好地理解经济现象的规律，预测未来的经济走势，为政府制定经济政策和企业经营决策提供科学依据。

希望以上案例可以帮助大家更好地理解计量经济学模型在实际应用中的重要性和价值。

【精品】计量经济学案例【案例一：经济增长与劳动力市场】计量经济学在劳动经济学中有着广泛的应用。

为了评估经济增长与劳动力市场之间的关系，可以使用生产函数模型，这一模型包括了劳动和资本等投入变量，以及一个因变量，即经济产出。

假设我们有一份涵盖了各个国家历年的GDP和劳动力人口的数据集，我们可以将数据设定为面板数据，并进行固定效应模型估计。

首先，我们需要对数据进行平稳性检验以避免伪回归。

我们可以用单位根检验，如ADF检验或IPS检验等来进行检查。

如果数据是平稳的，我们可以进行下一步，也就是估计生产函数模型。

如果我们发现劳动力和经济增长之间存在正相关关系，那么我们可能会得出结论：增加劳动力可以促进经济增长。

另一方面，如果资本和经济增长之间存在更强的关系，那么我们可能会建议政策制定者通过增加投资来刺激经济增长。

【案例二：价格与需求】计量经济学也被广泛应用于研究价格与需求之间的关系。

例如，在商品市场中，价格和需求之间存在负相关关系。

为了验证这一点，我们可以使用OLS估计法进行回归分析。

假设我们有一份包含各种商品价格和销售量的数据集。

我们可以将价格作为自变量，销售量作为因变量进行回归。

如果回归结果的斜率是负的，说明价格和销售量之间存在负相关关系，即当价格上升时，销售量会下降。

如果回归结果的斜率是正的，那么我们可能需要进一步检查数据是否存在异常值或者是否存在其他因素影响了结果。

通过这种分析，我们可以更好地理解价格和需求之间的关系，从而帮助政策制定者做出更好的决策。

例如，如果一个公司想要提高其产品的销售量，它可能需要考虑降低价格或者提供其他形式的促销活动。

【案例三：教育投资与经济增长】计量经济学也被广泛应用于研究教育投资与经济增长之间的关系。

一些研究表明，教育投资可以促进经济增长。

为了验证这一点，我们可以使用时间序列数据集进行回归分析。

假设我们有一份包含了各个国家历年的教育投资和GDP数据的时间序列数据集。

我们可以将教育投资作为自变量，GDP作为因变量进行回归。