计量经济学案例分析

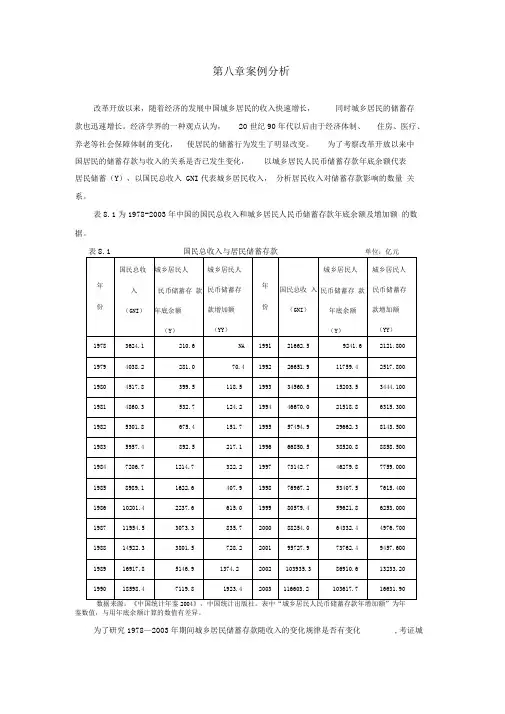
第八章案例分析改革开放以来，随着经济的发展中国城乡居民的收入快速增长，同时城乡居民的储蓄存款也迅速增长。

经济学界的一种观点认为，20世纪90年代以后由于经济体制、住房、医疗、养老等社会保障体制的变化，使居民的储蓄行为发生了明显改变。

为了考察改革开放以来中国居民的储蓄存款与收入的关系是否已发生变化，以城乡居民人民币储蓄存款年底余额代表居民储蓄（Y），以国民总收入GNI代表城乡居民收入，分析居民收入对储蓄存款影响的数量关系。

表8.1为1978-2003年中国的国民总收入和城乡居民人民币储蓄存款年底余额及增加额的数据。

单位：亿元2004鉴数值，与用年底余额计算的数值有差异。

为了研究1978—2003年期间城乡居民储蓄存款随收入的变化规律是否有变化,考证城乡居民储蓄存款、国民总收入随时间的变化情况，如下图所示:图8.5从图8.5中，尚无法得到居民的储蓄行为发生明显改变的详尽信息。

若取居民储蓄的增量（YY ）,并作时序图（见图 8.6）从居民储蓄增量图可以看出，城乡居民的储蓄行为表现出了明显的阶段特征:2000年有两个明显的转折点。

再从城乡居民储蓄存款增量与国民总收入之间关系的散布图看（见图8.7），也呈现出了相同的阶段性特征。

为了分析居民储蓄行为在 1996年前后和2000年前后三个阶段的数量关系，引入虚拟变 量D 和D2°D 和D 2的选择，是以1996>2000年两个转折点作为依据，1996年的GNI 为66850.50 亿元,2000年的GNI 为国为民8254.00亿元，并设定了如下以加法和乘法两种方式同时引入 虚拟变量的的模型:YY = 1+ 2GNI t3GNI t66850.50 D 1t+4GNh 88254.00 D2tiD1t 1996年以后 D1 t 2000年以后 其中:D1t_t 1996年及以前2t0 t 2000年及以前对上式进行回归后，有:Dependent Variable: YY Method: Least Squares Date: 06/16/05 Time: 23:27120000 8.71996年和100000-400002WMGNio eOB2&ISEea9a9l2949698[Ma220CUCir-“-1CC0C图8.6*OOCOmnoot ， RtKXD TconrGF*Sample (adjusted): 1979 2003Included observations: 25 after adjustmentsVariable Coefficient Std. Error t-Statistic Prob.C -830.4045 172.1626 -4.823374 0.0001 GNI0.144486 0.005740 25.17001 0.0000 (GNI-66850.50)*DUM1-0.291371 0.027182 -10.71920 0.0000 (GNI-88254.00)*DUM20.5602190.04013613.958100.0000R-squared0.989498 Mean dependent var 4168.652 Adjusted R-squared 0.987998 S.D. dependent var 4581.447 S.E. of regression 501.9182 Akaike info criterion 15.42040 Sum squared resid 5290359. Schwarz criterion 15.61542 Log likelihood -188.7550 F-statistic 659.5450 Durbin-Watson stat1.677712Prob(F-statistic)0.000000即有:YY = -830.4045 + 0.1445GNI t - 0.2914 GNI t -66850.50 6 + 0.5602 GNI t -88254.00 D ?tse= ( 172.1626) ( 0.0057) ( 0.0272) t = (-4.8234)(25.1700) (-10.7192)由于各个系数的t 检验均大于2，表明各解释变量的系数显著地不等于 存款年增加额的回归模型分别为:(0.0401)(13.9581)2 2R 0.9895 R 0.9880 F 659.5450 DW 1.6777 t 1996 1996<t 2000 t 20000，居民人民币储蓄YY = -830.4045 + 0.1445GNI t+ 1tYY YY = 18649.8312- 0.1469GNI t+ 2tYY =- 30790.0596 + 0.4133GNI t+ 3t这表明三个时期居民储蓄增加额的回归方程在统计意义上确实是不相同的。

美股行情对A股的影响性分析——标普500与沪深300相关性分析摘要：本文主要通过分析标准普尔500指数与沪深300指数的相关性，以标普500指数为解释变量，以沪深300指数为被解释变量，利用Eviews软件，使用其中的最小二乘法对其进行线性回归分析，最终得出方程。

并对其进行显著性检验（F，t）、异方差检验、自相关性检验来验证方程的可靠性。

然后解释方程的经济意义，并利用软件对未来指数变动进行预测。

最后在未来几天比较预测结果与实际两个指数的变化情况，验证实际应用情况。

关键词：标普500、沪深300、Eviews、显著性检验、异方差检验、自相关性检验。

一、研究背景1.全球化大环境在经济全球化不断深入发展的今天，全球资本市场，尤其是中美两个超级大国之间的资本流通，早已彼此嵌入，密不可分。

全世界早有不少学者对中美资本流通做了深入研究。

但美国股市发展早于中国十几年，其内部的资金也远远超过中国股市，美国股市的资本流动势必会对中国股市产生一定影响，这种影响不仅体现在情绪面，更反映在指数变动方向上。

2.对外开放资本市场的QFII政策Qualified Foreign Institutional Investor，作为一种过渡性制度安排，QFII制度是在资本项目尚未完全开放的国家和地区，实现有序、稳妥开放证券市场的特殊通道。

外资对中国股市的影响早已不可忽视，而美国市场的变动也一定程度会影响在中国股市外资的操作行为。

所以研究两个指数的变动是很有意义的。

二、数据1.数据选择沪深两个市场各自均有独立的综合指数和成份指数，这些指数不能用来反映沪深两市的整体情况，而沪深300指数则同时考虑了两市的交易情况，是中国A股市场的“晴雨表”。

标准普尔500指数英文简写为S&P 500 Index，是记录美国500家上市公司的一个股票指数。

与道琼斯指数等其他指数相比，标准普尔500指数包含的公司更多，因此风险更为分散，能够反映更广泛的市场变化。

案例分析1一、研究的目的要求居民消费在社会经济的持续发展中有着重要的作用。

居民合理的消费模式和居民适度的消费规模有利于经济持续健康的增长，而且这也是人民生活水平的具体体现。

改革开放以来随着中国经济的快速发展，人民生活水平不断提高，居民的消费水平也不断增长。

但是在看到这个整体趋势的同时，还应看到全国各地区经济发展速度不同，居民消费水平也有明显差异。

例如，2002年全国城市居民家庭平均每人每年消费支出为6029.88元, 最低的黑龙江省仅为人均4462.08元，最高的上海市达人均10464元，上海是黑龙江的2.35倍。

为了研究全国居民消费水平及其变动的原因，需要作具体的分析。

影响各地区居民消费支出有明显差异的因素可能很多，例如，居民的收入水平、就业状况、零售物价指数、利率、居民财产、购物环境等等都可能对居民消费有影响。

为了分析什么是影响各地区居民消费支出有明显差异的最主要因素，并分析影响因素与消费水平的数量关系，可以建立相应的计量经济模型去研究。

二、模型设定我们研究的对象是各地区居民消费的差异。

居民消费可分为城市居民消费和农村居民消费，由于各地区的城市与农村人口比例及经济结构有较大差异，最具有直接对比可比性的是城市居民消费。

而且，由于各地区人口和经济总量不同，只能用“城市居民每人每年的平均消费支出”来比较，而这正是可从统计年鉴中获得数据的变量。

所以模型的被解释变量Y 选定为“城市居民每人每年的平均消费支出”。

因为研究的目的是各地区城市居民消费的差异，并不是城市居民消费在不同时间的变动，所以应选择同一时期各地区城市居民的消费支出来建立模型。

因此建立的是2002年截面数据模型。

影响各地区城市居民人均消费支出有明显差异的因素有多种，但从理论和经验分析，最主要的影响因素应是居民收入，其他因素虽然对居民消费也有影响，但有的不易取得数据，如“居民财产”和“购物环境”；有的与居民收入可能高度相关，如“就业状况”、“居民财产”；还有的因素在运用截面数据时在地区间的差异并不大，如“零售物价指数”、“利率”。

南开大学《计量经济学》案例分析案例一：用回归模型预测木材剩余物（file:b1c3）伊春林区位于黑龙江省东北部。

全区有森林面积218.9732万公顷，木材蓄积量为2.324602亿m3。

森林覆盖率为62.5%，是我国主要的木材工业基地之一。

1999年伊春林区木材采伐量为532万m3。

按此速度44年之后，1999年的蓄积量将被采伐一空。

所以目前亟待调整木材采伐规划与方式，保护森林生态环境。

为缓解森林资源危机，并解决部分职工就业问题，除了做好木材的深加工外，还要充分利用木材剩余物生产林业产品，如纸浆、纸袋、纸板等。

因此预测林区的年木材剩余物是安排木材剩余物加工生产的一个关键环节。

下面，利用一元线性回归模型预测林区每年的木材剩余物。

显然引起木材剩余物变化的关键因素是年木材采伐量。

给出伊春林区16个林业局1999年木材剩余物和年木材采伐量数据如表1.1。

散点图见图1.1。

观测点近似服从线性关系。

建立一元线性回归模型如下：y t = β0 + β1 x t + u t表1.1 年剩余物y t和年木材采伐量x t数据林业局名年木材剩余物y t（万m3）年木材采伐量x t（万m3）乌伊岭26.13 61.4 东风23.49 48.3 新青21.97 51.8 红星11.53 35.9 五营7.18 17.8 上甘岭 6.80 17.0 友好18.43 55.0 翠峦11.69 32.7 乌马河 6.80 17.0 美溪9.69 27.3 大丰7.99 21.5 南岔12.15 35.5 带岭 6.80 17.0 朗乡17.20 50.0 桃山9.50 30.0 双丰 5.52 13.8合计202.87 532.00图1.1 年剩余物y t和年木材采伐量x t散点图图1.2 EViews输出结果EViews估计结果见图1.2。

在已建立Eviews数据文件的基础上，进行OLS估计的操作步骤如下：打开工作文件，从主菜单上点击Quick键，选Estimate Equation 功能。

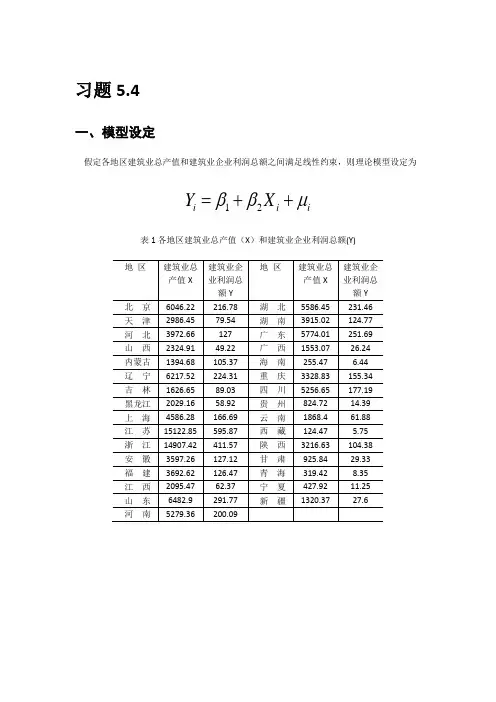
习题5.4一、模型设定假定各地区建筑业总产值和建筑业企业利润总额之间满足线性约束，则理论模型设定为表1各地区建筑业总产值（X ）和建筑业企业利润总额(Y)i i i X Y μββ++=21二、参数估计估计结果为=2.368138+0.034980t=(0.261691) (19.94530)=0.932055 F=397.8152iY ˆiX 2R三、检验模型的异方差（一）goldfeld-quandt检验由图得到残差平方和21i=5739.944，残差平方和22i=23084.48 ,根据goldfeld-quandt检验，F统计量为F===4.0217在α=0.05下,式中α分子、分母的自由度均为10，查F分母表得临界值F0.05（10,10）=2.98，因为F=4.0217>F0.05(10,10)=2.98,所以拒绝原假设，表明模型确实存在异方差（二）White检验根据White检验中辅助函数的构造，则辅助函数为经估计出现White 检验结果，见图从图可以看出，n =20.15100,由White 检验知，查分布表，得临界值(2)=5.9915,同时X 和的t 检验也显著。

比较计算的统计量与临界值，因为n =20.15100>(2)=5.9915，所以拒绝原假设，不拒绝备择假设，表明模型存在异方差。

四、异方差性的修正在运用WLS 法估计中，可以分别选中各种权数做比较，从中则较为理想的权数。

经估计检验用权数1/X t 2的效果最好。

下图为估计结果tt t tv x x +∂+∂+∂=22102σ2R 2χ205.0χ2X 2R 205.0χ可以看出，运用加权最小二乘法消除了预防差性后，参数的t 检验均显著，F 检验也显著，即估计结果为t=(8.303693) (6.569011)=0.976392 DW=1.816022 F=43.15191五．结论这说明个地区建筑业总产值每增加1元，平均来说将增加0.018026元建筑业企业利润总额，而不是引子中得出的需要增加0.37627元建筑业企业利润总额。

第七章 案例分析【案例7.1】 为了研究1955—1974年期间美国制造业库存量Y 和销售额X 的关系，我们在例7.3中采用了经验加权法估计分布滞后模型。

尽管经验加权法具有一些优点，但是设置权数的主观随意性较大，要求分析者对实际问题的特征有比较透彻的了解。

下面用阿尔蒙法估计如下有限分布滞后模型：tt t t t t u X X X X Y +++++=---3322110ββββα将系数i β(i =0,1,2,3)用二次多项式近似，即00αβ=2101αααβ++=210242αααβ++= 210393αααβ++=则原模型可变为t t t t t u Z Z Z Y ++++=221100αααα其中3212321132109432---------++=++=+++=t t t t t t t t t t t t t X X X Z X X X Z X X X X Z在Eviews 工作文件中输入X 和Y 的数据，在工作文件窗口中点击“Genr ”工具栏，出现对话框，输入生成变量Z 0t 的公式，点击“OK ”；类似，可生成Z 1t 、Z 2t 变量的数据。

进入Equation Specification 对话栏，键入回归方程形式Y C Z0 Z1 Z2点击“OK ”，显示回归结果（见表7.2）。

表7.2表中Z0、 Z1、Z2对应的系数分别为210ααα、、的估计值210ˆˆˆααα、、。

将它们代入分布滞后系数的阿尔蒙多项式中，可计算出3210ˆˆˆˆββββ、、、的估计值为： -0.522)432155.0(9902049.03661248.0ˆ9ˆ3ˆˆ0.736725)432155.0(4902049.02661248.0ˆ4ˆ2ˆˆ 1.131142)432155.0(902049.0661248.0ˆˆˆˆ661248.0ˆˆ21012101210100=-⨯+⨯+=++==-⨯+⨯+=++==-++=++===αααβαααβαααβαβ从而，分布滞后模型的最终估计式为：32155495.076178.015686.1630281.0419601.6----+++-=t t t t t X X X X Y在实际应用中，Eviews 提供了多项式分布滞后指令“PDL ”用于估计分布滞后模型。

【精品】计量经济学案例【案例一：经济增长与劳动力市场】计量经济学在劳动经济学中有着广泛的应用。

为了评估经济增长与劳动力市场之间的关系，可以使用生产函数模型，这一模型包括了劳动和资本等投入变量，以及一个因变量，即经济产出。

假设我们有一份涵盖了各个国家历年的GDP和劳动力人口的数据集，我们可以将数据设定为面板数据，并进行固定效应模型估计。

首先，我们需要对数据进行平稳性检验以避免伪回归。

我们可以用单位根检验，如ADF检验或IPS检验等来进行检查。

如果数据是平稳的，我们可以进行下一步，也就是估计生产函数模型。

如果我们发现劳动力和经济增长之间存在正相关关系，那么我们可能会得出结论：增加劳动力可以促进经济增长。

另一方面，如果资本和经济增长之间存在更强的关系，那么我们可能会建议政策制定者通过增加投资来刺激经济增长。

【案例二：价格与需求】计量经济学也被广泛应用于研究价格与需求之间的关系。

例如，在商品市场中，价格和需求之间存在负相关关系。

为了验证这一点，我们可以使用OLS估计法进行回归分析。

假设我们有一份包含各种商品价格和销售量的数据集。

我们可以将价格作为自变量，销售量作为因变量进行回归。

如果回归结果的斜率是负的，说明价格和销售量之间存在负相关关系，即当价格上升时，销售量会下降。

如果回归结果的斜率是正的，那么我们可能需要进一步检查数据是否存在异常值或者是否存在其他因素影响了结果。

通过这种分析，我们可以更好地理解价格和需求之间的关系，从而帮助政策制定者做出更好的决策。

例如，如果一个公司想要提高其产品的销售量，它可能需要考虑降低价格或者提供其他形式的促销活动。

【案例三：教育投资与经济增长】计量经济学也被广泛应用于研究教育投资与经济增长之间的关系。

一些研究表明，教育投资可以促进经济增长。

为了验证这一点，我们可以使用时间序列数据集进行回归分析。

假设我们有一份包含了各个国家历年的教育投资和GDP数据的时间序列数据集。

我们可以将教育投资作为自变量，GDP作为因变量进行回归。

计量经济学案例分析一、问题提出国内生产总值（GDP）指一个国家或地区所有常住单位在一定时期内(通常为1 年)生产活动的最终成果，即所有常住机构单位或产业部门一定时期内生产的可供最终使用的产品和劳务的价值，包括全部生产活动的成果，是一个颇为全面的经济指标。

对国内生产总值的分析研究具有极其重要的作用和意义，可以充分地体现出一个国家的综合实力和竞争力。

因此，运用计量经济学的研究方法具体分析国内生产总值和其他经济指标的相关关系。

对预测国民经济发展态势，制定国家宏观经济政策，保持国民经济平稳地发展具有重要的意义。

二、模型变量的选择模型中的被解释变量为国内生产总值Y。

影响国内生产总值的因素比较多，根据其影响因素的大小和资料的可比以及预测模型的要求等方面原因, 文章选择以下指标作为模型的解释变量：固定资产投资总量(X1 ) 、财政支出总量(X2 )、城乡居民储蓄存款年末余额(X3 )、进出口总额(X4 )、上一期国内生产总值(X5)、职工工资总额(X6)。

其中，固定资产投资的增长是国内生产总值增长的重要保障，影响效果显著；财政支出是扩大内需的保证，有利于国内生产总值的增长；城乡居民储蓄能够促进国内生产总值的增长，是扩大投资的重要因素，但是过多的储蓄也会减缓经济的发展；进出口总额反映了一个国家或地区的经济实力；上期国内生产总值是下期国内生产总值增长的基础；职工工资总额是国内生产总值规模的表现。

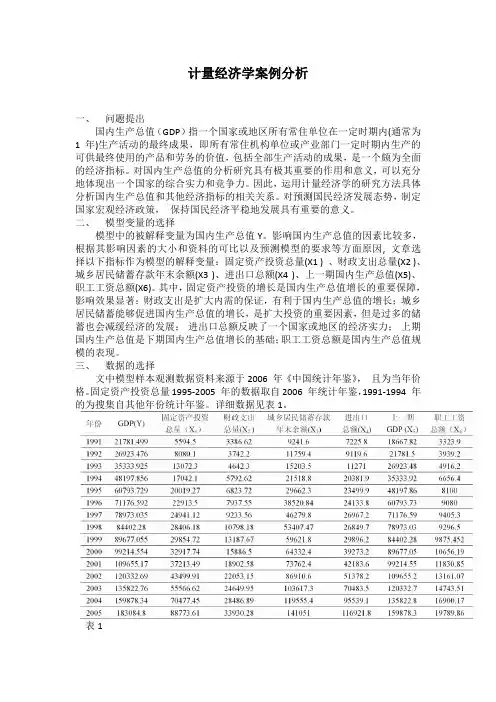
三、数据的选择文中模型样本观测数据资料来源于2006 年《中国统计年鉴》，且为当年价格。

固定资产投资总量1995-2005 年的数据取自2006 年统计年鉴，1991-1994 年的为搜集自其他年份统计年鉴。

详细数据见表1。

表1四、模型的建立通过散点图可以发现，被解释变量Y与解释变量：X1、X2、X3、X4、X5、X6 之间大致存在线性相关关系。

于是可以设该模型的理论方程：Y =β0 +β1X1 +β2 X2 +β3 X3 +β4 X4+β5 X5 +β6X6+u (1)五、模型的参数估计对于理论模型运用OLS进行参数估计,再用Eviews软件进行运算,得到的结果如下:Y(^)=-2343.173-0.232209X1+0.285821X2-0.090052X3+0.265575X4+0.653820X5 +3.810634X6 (2)t =（-0.867663）（-0.663590）（0.569626）（-0.295743）（1.144851）（3.051578）（3.743547）R²=0.999342 D.W.=2.181505 F=2023.923六、模型的检验1、经济意义检验上面模型(2)可以看出β1<0，这表明随着固定资产投资总额的增加，国内生产总值反而减少，这是不符合实际的，因此不能通过经济意义检验，把此变量剔除。