正态总体的置信区间

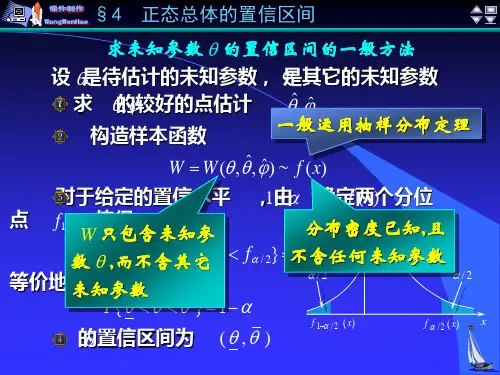
第四节 正态总体的置信区间与其他总体相比, 正态总体参数的置信区间是最完善的,应用也最广泛。

在构造正态总体参数的置信区间的过程中，t 分布、2χ分布、F 分布以及标准正态分布)1,0(N 扮演了重要角色.本节介绍正态总体的置信区间,讨论下列情形: 1. 单正态总体均值(方差已知)的置信区间; 2. 单正态总体均值(方差未知)的置信区间; 3. 单正态总体方差的置信区间;4. 双正态总体均值差(方差已知)的置信区间;5. 双正态总体均值差(方差未知但相等)的置信区间;6. 双正态总体方差比的置信区间.注: 由于正态分布具有对称性, 利用双侧分位数来计算未知参数的置信度为α-1的置信区间, 其区间长度在所有这类区间中是最短的.分布图示★ 引言★ 单正态总体均值（方差已知）的置信区间★ 例1 ★ 例2★ 单正态总体均值（方差未知）的置信区间 ★ 例3 ★ 例4★ 单正态总体方差的置信区间 ★ 例5 ★ 双正态总体均值差（方差已知）的置信区间 ★ 例6 ★ 双正态总体均值差（方差未知）的置信区间★ 例7 ★ 例8★ 双正态总体方差比的置信区间 ★ 例9 ★ 内容小结 ★ 课堂练习 ★ 习题6-4内容要点一、单正态总体均值的置信区间(1)设总体),,(~2σμN X 其中2σ已知, 而μ为未知参数, n X X X ,,,21 是取自总体X 的一个样本. 对给定的置信水平α-1, 由上节例1已经得到μ的置信区间,,2/2/⎪⎪⎭⎫⎝⎛⋅+⋅-n u X n u X σσαα二、单正态总体均值的置信区间(2)设总体),,(~2σμN X 其中μ,2σ未知, n X X X ,,,21 是取自总体X 的一个样本. 此时可用2σ的无偏估计2S 代替2σ, 构造统计量n S X T /μ-=,从第五章第三节的定理知).1(~/--=n t nS X T μ对给定的置信水平α-1, 由αμαα-=⎭⎬⎫⎩⎨⎧-<-<--1)1(/)1(2/2/n t n S X n t P ,即 ,1)1()1(2/2/αμαα-=⎭⎬⎫⎩⎨⎧⋅-+<<⋅--n S n t X n S n t X P因此, 均值μ的α-1置信区间为.)1(,)1(2/2/⎪⎪⎭⎫ ⎝⎛⋅-+⋅--n S n t X n S n t X αα三、单正态总体方差的置信区间上面给出了总体均值μ的区间估计，在实际问题中要考虑精度或稳定性时，需要对正态总体的方差2σ进行区间估计.设总体),,(~2σμN X 其中μ,2σ未知,n X X X ,,,21 是取自总体X 的一个样本. 求方差2σ的置信度为α-1的置信区间. 2σ的无偏估计为2S , 从第五章第三节的定理知,)1(~1222--n S n χσ, 对给定的置信水平α-1, 由,1)1()1()1()1(,1)1(1)1(22/12222/222/2222/1αχσχαχσχαααα-=⎪⎭⎪⎬⎫⎪⎩⎪⎨⎧--<<---=⎭⎬⎫⎩⎨⎧-<-<---n S n n Sn P n S n n P 于是方差2σ的α-1置信区间为⎪⎪⎭⎫ ⎝⎛-----)1()1(,)1()1(22/1222/2n S n n S n ααχχ而方差σ的α-1置信区间.)1()1(,)1()1(22/1222/2⎪⎪⎭⎫ ⎝⎛-----n S n n S n ααχχ四、双正态总体均值差的置信区间(1)在实际问题中，往往要知道两个正态总体均值之间或方差之间是否有差异，从而要研究两个正态总体的均值差或者方差比的置信区间。

正态分布总体总体均值已知方差的置信区间【文章开头】一、引言在统计学中，正态分布总体是相当常见的一种总体类型。

当我们需要对一个正态分布总体的总体均值进行推断时，有时候我们会面临到总体均值已知，但方差未知的情况。

对于这样的情况，我们可以使用置信区间来进行推断。

二、什么是置信区间？置信区间是指在统计推断中，对总体参数的估计范围。

通常，我们会给出一个置信水平，比如95%的置信水平，表示对总体参数的估计有95%的把握是正确的。

置信区间由一个下限和一个上限组成，表示总体参数可能落在这个范围内的概率。

三、正态分布总体的总体均值已知的情况下，方差的置信区间如何计算？当正态分布总体的总体均值已知时，我们可以使用样本标准差来作为总体方差的估计。

我们可以利用样本大小、置信水平和样本标准差来计算方差的置信区间。

四、计算步骤1. 收集样本数据：从正态分布总体中随机抽取样本，并记录样本数据。

2. 计算样本标准差：利用样本数据计算样本标准差。

样本标准差是总体方差的一个无偏估计。

3. 确定置信水平：根据需要的置信水平，确定置信水平对应的临界值。

临界值可以从统计表中查找。

4. 计算置信区间：利用样本大小、样本标准差和置信水平的临界值，计算方差的置信区间。

五、示例假设我们想研究某种药物对血压的影响。

我们从正态分布的总体中随机抽取了100个样本，并记录了每个样本的血压数据。

我们已知总体均值为120，方差未知。

现在，我们想要计算方差的95%置信区间。

1. 收集样本数据：从正态分布总体中随机抽取100个样本，并记录血压数据。

2. 计算样本标准差：利用样本数据计算样本标准差。

假设计算得到样本标准差为10。

3. 确定置信水平：我们希望得到95%的置信区间，因此置信水平为0.95。

4. 计算置信区间：根据样本大小100，样本标准差10，和置信水平0.95的临界值，我们可以计算得到方差的置信区间。

【文章主体】六、方差的置信区间是如何帮助我们进行推断的？方差的置信区间为我们提供了一个总体参数可能的取值范围。

正态分布的置信区间
置信区间的常用计算方法如下：
pr(c1\uc=μ\uc=c2)=1-α
其中：α就是显著性水平（基准：0.05或0.10）；
pr表示概率，是单词probability的缩写；
%*(1-α)或(1-α)或指置信水平（比如：95%或0.95）；
表达方式：interval(c1,c2) - 置信区间。

资料开拓：
置信区间是指由样本统计量所构造的总体参数的估计区间。

在统计学中，一个概率样
本的置信区间（confidence interval）是对这个样本的某个总体参数的区间估计。

置信
区间展现的是这个参数的真实值有一定概率落在测量结果的周围的程度，其给出的是被测
量参数的测量值的可信程度，即前面所要求的“一个概率”。

置信区间就是一种常用的区间估算方法，所谓置信区间就是分别以统计数据量的置信
下限和置信上限为上下界形成的区间。

对于一组取值的样本数据，其平均值为μ，标准
偏差为σ，则其整体数据的平均值的(1-α)%置信区间为(μ-ζα/2σ , μ+ζα/2σ) ，其中α为非置信水平在正态分布内的覆盖面积，ζα/2即为对应的标准分数。

两正态总体均值差的区间估计基于Wolfram Mathematica ,给出了两正态分布Ν[μ1,σ1]、Ν[μ2,σ2]总体均值差μ1-μ2在两总体方差已知、未知但相等、未知但样本量相等、未知但已知方差比、未知近似、未知精确的置信区间估计方法。

最后对理论结果进行程序模拟。

设X i ~Ν(μ1,σ1),i =1,2,...,n ，为正态总体X ~Ν(μ1,σ1)的一i.i.d.，样本均值X -=1n i =1n X i ，样本方差S X 2=1n -1 i =1n X i -X - 2。

设Y i ~Ν(μ2,σ2),i =1,2,...,m ，为正态总体Y ~Ν(μ2,σ2)的一i.i.d.，样本均值Y -=1m i =1m Y i ，样本方差S Y 2=1m -1 i =1m Y i -Y - 2。

一、两总体方差σ12=σ102、σ22=σ202已知定理1：X -Ν μ1,σ1n ,Y -Ν μ2,σ2m .CharacteristicFunction NormalDistribution [μ,σ],t n n;特征函数CharacteristicFunction 正态分布NormalDistribution μ,σn ,t ;%⩵%%//完全简化FullSimplify [#,n >0&&属于Element [n,整数域Integers ]]&True定理2：X --Y -Νμ1-μ2,⇔X --Y --(μ1-μ2)Ν[0,1].转换分布TransformedDistribution X -Y,X 正态分布NormalDistribution μ1,σ1n ,Y 正态分布NormalDistribution μ2,σ2m转换分布TransformedDistribution(X -Y )-(μ1-μ2), X 正态分布NormalDistribution μ1,σ1n ,Y 正态分布NormalDistribution μ2,σ2m //完全简化FullSimplifyNormalDistribution μ1-μ2,NormalDistribution [0,1]下面简要给出求μ1-μ2置信区间的方法：由α2≤Φ≤1-α2,得μ1-μ2的置信水平为1-α的置信区间为X --Y --Z1≤μ1-μ2≤X --Y --Zα2即X --Y --Z1-α2≤μ1-μ2≤X --Y -+Z1其长度：L =2Z 1-α2以下是程序模拟：需要Needs ["HypothesisTesting`"]μ10=10;μ20=1;σ10=3;σ20=4;X =伪随机变数RandomVariate [正态分布NormalDistribution [μ10,σ10],2000];Y =伪随机变数RandomVariate [正态分布NormalDistribution [μ20,σ20],1000];α=0.05;"(一)两方差已知""1.计算法"n =长度Length [X ];m =长度Length [Y ];M =平均值Mean [X ]-平均值Mean [Y ];σ=Q =分位数Quantile 正态分布NormalDistribution [0,1],1-α2;{M -Q σ,M +Q σ}"2.MeanDifferenceCI"MeanDifferenceCI X,Y,KnownVariance → σ102,σ202 ,置信级别ConfidenceLevel →1-α"3.NormalCI"NormalCI [M,σ,置信级别ConfidenceLevel →1-α]"区间长度："L =2Q σ"相对区间长度："r =L M "(二)两方差未知"清除Clear [μ,σ]{μ1,σ1}={μ,σ}/.求分布参数FindDistributionParameters [X,正态分布NormalDistribution [μ,σ]];2 正态分布\\正态分布统计分析\\两正态总体均值差的置信区间.nb求分布参数正态分布{μ2,σ2}={μ,σ}/.求分布参数FindDistributionParameters [Y,正态分布NormalDistribution [μ,σ]];"1.计算法"n =长度Length [X ];m =长度Length [Y ];M =平均值Mean [X ]-平均值Mean [Y ];σ=Q =分位数Quantile 正态分布NormalDistribution [0,1],1-α2;{M -Q σ,M +Q σ}"2.MeanDifferenceCI"MeanDifferenceCI X,Y,KnownVariance → σ12,σ22 ,置信级别ConfidenceLevel →1-α"3.NormalCI"NormalCI [M,σ,置信级别ConfidenceLevel →1-α]"区间长度："L =2Q σ"相对区间长度："r =L M(一)两方差已知1.计算法{8.75322,9.31447}2.MeanDifferenceCI {8.75322,9.31447}3.NormalCI{8.75322,9.31447}区间长度：0.561248相对区间长度：0.0621273(二)两方差未知1.计算法{8.75899,9.30871}2.MeanDifferenceCI {8.75899,9.30871}3.NormalCI{8.75899,9.30871}区间长度：正态分布\\正态分布统计分析\\两正态总体均值差的置信区间.nb30.549724相对区间长度：0.0608516二、两总体方差σ12=σ22未知σ12=σ22未知,由定理2,知X--Y- Ν μ1-μ2,σ,X--Y- -(μ1-μ2)σΝ[0,1]。

如何确定正态分布总体均值已知的方差的置信区间在统计学中，置信区间是一种用来估计参数真实值范围的方法。

当我们知道总体均值，但方差未知时，我们需要确定正态分布总体总体均值已知的方差的置信区间。

在本文中，我将以从简到繁的方式来探讨这个主题，让您能更深入地理解。

1. 正态分布总体的概念让我们简要回顾一下正态分布总体的概念。

正态分布是最为常见的概率分布之一，其特点是呈钟形曲线，均值和标准差决定了曲线的中心位置和宽度。

在统计学中，我们常常使用正态分布来描述连续型随机变量的分布情况。

2. 总体均值已知的情况当我们已经知道正态分布总体的均值时，我们可以通过样本来估计总体的方差。

我们可以利用样本方差来估计总体方差，然后构建置信区间来确定总体方差的范围。

3. 方差的置信区间估计为了确定正态分布总体均值已知的方差的置信区间，我们可以利用卡方分布来进行估计。

卡方分布是一种特殊的概率分布，用于描述正态分布总体方差的抽样分布。

通过卡方分布的性质，我们可以构建出方差的置信区间，从而对总体方差做出估计。

4. 个人观点和理解在我的个人观点中，确定正态分布总体总体均值已知的方差的置信区间是统计学中非常重要的一部分。

这不仅可以帮助我们对总体方差进行估计，还可以为我们后续的推断统计提供重要的依据。

通过合理地构建置信区间，我们可以更准确地对总体参数进行推断，并且可以对我们的结论进行更加可靠的评估。

总结通过本文的阐述，我们可以深刻理解确定正态分布总体总体均值已知的方差的置信区间的方法。

我们需要对正态分布总体及其性质有一个清晰的认识。

我们可以利用样本数据来对总体方差进行估计，并且通过卡方分布来构建置信区间。

我也共享了我个人的观点和理解，希望可以为您对这个主题提供更多的思考。

在知识的文章格式中，可以使用序号标注来清晰地展示每个步骤的逻辑关系。

我希望本文的内容能够帮助您更好地理解正态分布总体总体均值已知的方差的置信区间的确定方法。

在统计学中，确定正态分布总体均值已知的方差的置信区间是一项重要的任务。