当前位置：文档之家 › 离散傅里叶变换和快速傅里叶变换

离散傅里叶变换和快速傅里叶变换

  • 格式：docx
  • 大小：326.50 KB
  • 文档页数：19

下载文档原格式

  / 19

合集下载

快速傅立叶变换和离散小波变换

快速傅立叶变换和离散小波变换

N
M
现的规律相似。分解多步后非零项的个数可能比输入序列的长度增加较多。例如，若输入序
1 2 3 4 列长度为 100，N=4，则 d k 有 51 项非零， d k 有 27 项非零， d k 有 15 项非零， d k 有 9 项非 5 6 6 零， d k 有 6 项非零， d k 有 4 项非零， c k 有 4 项非零。这样分解到 6 步后得到的序列的非
j cij 1 cij 1 hk c(k 2i) mod n ,
di j 1 di j 1 g k d(jk 2i ) modn
end for end for (2.2)j=j+1, n=n/2 end while End 显然，算法 22.3 的时间复杂度为 O(N*L)。 在实际应用中，很多情况下采用紧支集小波（Compactly Supported Wavelets） ，这时相 应的尺度系数和小波系数都是有限长度的，不失一般性设尺度系数只有有限个非零值： h1,„,hN，N 为偶数，同样取小波使其只有有限个非零值：g1,„,gN。为简单起见，设尺度系
0 xn , n 1,2,, M (其余点的值都 数与小波函数都是实数。对有限长度的输入数据序列： cn
看成 0)，它的离散小波变换为:
c kj 1 c nj hn 2 k
nZ
d kj 1 c nj g n 2 k
nZ
j 0,1, , J 1
其中 J 为实际中要求分解的步数，最多不超过 log2M，其逆变换为
j
c1 k x n hn 2 k
n 1
M 1 dk x n g n2k n 1
M
不 难 看 出 ， c1 k 的 非 零 值 范 围 为 ： k 2 1,,1,0,, 2 1, 即 有

离散傅里叶变换和快速傅里叶变换的区别

离散傅里叶变换和快速傅里叶变换的区别

离散傅里叶变换和快速傅里叶变换的区别离散傅里叶变换（Discrete Fourier Transform，DFT）和快速傅里叶变换（Fast Fourier Transform，FFT）都是数字信号处理中常用的算法，用于将时域信号转换为频域信号。

虽然它们都是傅里叶变换的变种，但它们之间有很大的区别。

DFT是一种直接计算傅里叶变换的方法，它将N个时域采样点转换为N个频域采样点。

DFT的计算复杂度为O(N^2)，因此对于大规模的信号处理任务来说，计算时间会非常长。

而FFT是一种基于分治思想的算法，它将DFT的计算复杂度降低到O(NlogN)，因此计算速度非常快，特别适合于大规模信号处理任务。

DFT和FFT的计算方式也有所不同。

DFT的计算公式为：X[k] = sum(x[n] * exp(-j*2*pi*k*n/N))其中，x[n]表示时域采样点，X[k]表示频域采样点，N表示采样点数，k和n分别表示频域和时域的索引。

这个公式需要进行N^2次复数乘法和加法运算，因此计算复杂度很高。

FFT的计算方式则是将DFT的计算过程分解为多个子问题，然后递归地求解这些子问题。

具体来说，FFT将N个采样点分为两个子序列，分别进行DFT计算，然后将它们合并起来得到整个序列的DFT结果。

这个过程可以递归地进行下去，直到只剩下一个采样点为止。

由于FFT采用了分治思想，它的计算复杂度为O(NlogN)，比DFT快得多。

DFT和FFT的应用场景也有所不同。

由于DFT的计算复杂度较高，因此它适合于小规模的信号处理任务，例如音频信号的处理。

而FFT则适合于大规模的信号处理任务，例如图像处理和视频处理。

此外，FFT还可以用于信号压缩、滤波和频域分析等领域。

离散傅里叶变换和快速傅里叶变换虽然都是傅里叶变换的变种，但它们之间有很大的区别。

DFT是一种直接计算傅里叶变换的方法，计算复杂度较高，适合于小规模的信号处理任务；而FFT是一种基于分治思想的算法，计算速度非常快，适合于大规模的信号处理任务。

快速傅里叶变换

快速傅里叶变换

快速傅⾥叶变换快速傅⾥叶变换快速傅⾥叶变换（FFT ）是根据计算量的最⼩化原理来设计和实施离散傅⾥叶变换(DFT)计算的⽅法。

1965年，库利（T.W.Cooley ）和图基（J.W.tukey ）发表了著名的《计算机计算傅⾥叶级数的⼀种算法》论⽂。

从此掀起了快速傅⾥叶变换计算⽅法研究的热潮。

快速傅⾥叶变换（FFT ）的出现，实现了快速、⾼效的信号分析和信号处理，为离散傅⾥叶变换(DFT)的⼴泛应⽤奠定了基础。

1.1离散傅⾥叶变换(DFT)的计算设x(n)是⼀个长度为M 的有限长序列，则定义x(n)的N 点离散傅⾥叶变换为∑-===10)()]([)(N n kn NW n x n x DFT k X 其中由于计算⼀个X(k)值需要N 次复乘法和(N-1)次复数加法，因⽽计算N 个X(k)值，共需N2次复乘法和N(N-1)次复加法。

每次复乘法包括4次实数乘法和2次实数加法，每次复加法包括2次实数加法，因此计算N 点的DFT 共需要4N2次实数乘法和(2N2+2N ·(N-1))次实数加法。

当N 很⼤时，这是⼀个⾮常⼤的计算量。

1.2减少DFT 计算量的⽅法减少DFT 的计算量的主要途径是利⽤k N W 的性质和计算表达式的组合使⽤，其本质是减少DFT 计算的点数N 以便减少DFT 的计算量。

k N W 的性质：（1）对称性： (2)周期性： (3) 可约性： (4) 特殊点：选择其中⼀个证明N N j k N j N k N j N k N e e e W 222)2(22πππ--+-+==ππj k N j e e --=2k N j e π2--=k N W -=FFT 算法是基于可以将⼀个长度为N 的序列的离散傅⾥叶变换逐次分解为较短的离散傅⾥叶变换来计算这⼀基本原理的。

这⼀原理产⽣了许多不同的算法，但它们在计算速度上均取得了⼤致相当的改善。

0,1,,1k N =-()*nk nk N N W W -=()()nk N n k n N k N N NW W W ++==nk mnk N mN W W =//nk nk m N N mW W =01N W =/21N N W =-(/2)k N k N NW W +=-在这⾥讨论两类基本的FFT 算法。

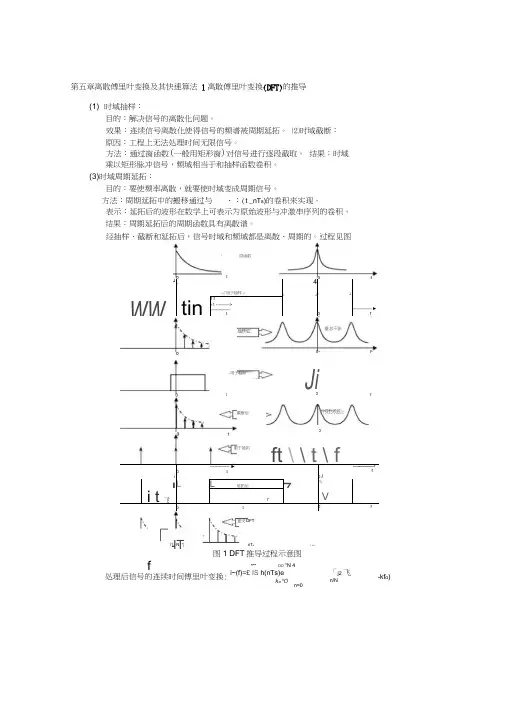
离散傅里叶变换及其快速算法

离散傅里叶变换及其快速算法

第五章离散傅里叶变换及其快速算法 1离散傅里叶变换(DFT)的推导(1) 时域抽样：目的：解决信号的离散化问题。

效果：连续信号离散化使得信号的频谱被周期延拓。

⑵时域截断： 原因：工程上无法处理时间无限信号。

方法：通过窗函数(一般用矩形窗)对信号进行逐段截取。

结果：时域乘以矩形脉冲信号，频域相当于和抽样函数卷积。

(3)时域周期延拓：目的：要使频率离散，就要使时域变成周期信号。

方法：周期延拓中的搬移通过与 、：(t _nT s )的卷积来实现。

表示：延拓后的波形在数学上可表示为原始波形与冲激串序列的卷积。

结果：周期延拓后的周期函数具有离散谱。

经抽样、截断和延拓后，信号时域和频域都是离散、周期的。

过程见图抽样后0 fJif-用于截断原函数J L<Z 用于抽样i4LJI Ji WWtin1 f=1 ----------> --------------t-------------- ►fVtt截断后有卷积波纹i------------- ►t0 I------------------ rfJL 」L延拓后7角ii t飞7Vtfft \ \ t \ f定义DFT用于延拓「ITf处理后信号的连续时间傅里叶变换:I'U N *|nT sr 0 N图1 DFT 推导过程示意图〜 oo "N 4l ~(f)=£ IS h(nTs)ek =^O「j2 飞n/Nn=0-kf o )(i) l~(f)是离散函数，仅在离散频率点f二kf o k—处存在冲激，强度为a k,其T o NT s余各点为0。

〜N N 1(ii) H(f)是周期函数，周期为Nf o == 工，每个周期内有N个不同的幅值。

T o NT s T s(iii) 时域的离散时间间隔(或周期)与频域的周期(或离散间隔)互为倒数。

2 DFT及IDFT的定义DFT定义：设hnT s是连续函数h(t)的N个抽样值n=0,1,…,N J，这N个点的宽度为N 的DFT 为：DFT N h(nT s)]=^ h(nT s)e」2邢/N =H —— J (k =0,1,…，N _1)7 l NT s 丿IDFT定义：设H 上是连续频率函数H(f)的N个抽样值k =0,1，…，N J，这N个点(NT s 丿的宽度为N的IDFT为：DFT N1 H k丄7 H L e」2「nk/N厶nTs , (k =0,1,…，N —1)|L Ns N k 卫NT se^Rk/N称为N点DFT的变换核函数，e j2 flk/N称为N点IDFT的变换核函数。

五种傅里叶变换

五种傅里叶变换

五种傅里叶变换傅里叶变换是一种将信号从时域转换到频域的数学工具，它在信号处理、图像处理、通信等领域都有广泛的应用。

傅里叶变换可以分为五种：离散傅里叶变换（DFT）、快速傅里叶变换（FFT）、连续时间傅里叶变换（CTFT）、离散时间傅里叶变换（DTFT）和希尔伯特-黄变换（HHT）。

一、离散傅里叶变换（DFT）离散傅里叶变换是指将一个有限长的离散序列，通过一定的算法转化成一个同样长度的复数序列。

它是一种计算量较大的方法，但在某些情况下精度更高。

DFT 的公式如下：$$F(k)=\sum_{n=0}^{N-1}f(n)e^{-i2\pi kn/N}$$其中 $f(n)$ 是原始信号，$F(k)$ 是频域表示。

二、快速傅里叶变换（FFT）快速傅里叶变换是一种计算 DFT 的高效算法，它可以减少计算量从而加快计算速度。

FFT 的实现方法有多种，其中最常用的是蝴蝶运算法。

FFT 的公式与 DFT 相同，但计算方法不同。

三、连续时间傅里叶变换（CTFT）连续时间傅里叶变换是指将一个连续的时间信号，通过一定的算法转化成一个连续的频域函数。

CTFT 的公式如下：$$F(\omega)=\int_{-\infty}^{\infty}f(t)e^{-i\omega t}dt$$其中 $f(t)$ 是原始信号，$F(\omega)$ 是频域表示。

四、离散时间傅里叶变换（DTFT）离散时间傅里叶变换是指将一个无限长的离散序列，通过一定的算法转化成一个同样长度的周期性复数序列。

DTFT 的公式如下：$$F(e^{j\omega})=\sum_{n=-\infty}^{\infty}f(n)e^{-j\omegan}$$其中 $f(n)$ 是原始信号，$F(e^{j\omega})$ 是频域表示。

五、希尔伯特-黄变换（HHT）希尔伯特-黄变换是一种基于经验模态分解（EMD）和 Hilbert 变换的非线性时频分析方法。

它可以对非平稳信号进行时频分析，并提取出信号中的本征模态函数（IMF）。

离散傅里叶变换的基本性质

离散傅里叶变换的基本性质

x(5 )
A(6 )
W
0 N
x(3 )
A(7 )
x(7 )
W
0 N
A(0 )
A(1 )
A(2 )
W
0 N
A(3 )
W
2 N
A(4 )
A(5 )
A(6 )
W
0 N
A(7 )
W
2 N
A(0 )
A(1 )
A(2 )
A(3 )
A(4 )
W
0 N
A(5 )
W
1 N
A(6 )
W
2 N
A(7 )
W
3 N
N点DIT―FFT运算流图(N=8)
A(5 )
A(6 )
W
0 N
A(7 )
W
2 N
A(0 )
A(1 )
A(2 )
A(3 )
A(4 )
W
0 N
A(5 )
W
1 N
A(6 )
W
2 N
A(7 )
W
3 N
N点DIT―FFT运算流图(N=8)
A(0 ) X(0 ) X(1 ) X(2 ) X(3 ) X(4 ) X(5 ) X(6 )
A(7 ) X(7 )
m N
WN 2
WNm
2. 时域抽取法基2FFT基本原理 FFT算法基本上分为两大类：
时域抽取法FFT(Decimation In Time FFT,简称DITFFT)和频域抽取法FFT(Decimation In Frequency FFT,简 称DIF―FFT)。下面先介绍DIF―FFT算法。
设序列x(n)的长度为N，且满足
N 2M , M 为自然数

信号分析与处理-14

信号分析与处理-14

X (e j )e j n d
连续且周期
X (e j ( 2 k )） X (e j）
西安工业大学
3.2 离散时间信号的傅里叶变换 三、离散时间信号的傅里叶变换
时间离散
X s ( j ) N /T 2 T

T

T
2 T
信号经采样， 时域离散，但 离散时间信号 的傅里叶变换 依然是连续的 ，计算机还是 没办法处理。
X (e ) x(n)e jn
j n 0 N 1
X (k ) x(n)WN kn
n 0
N 1
X (k ) X (e j ) |

2 k N
结论：DFT是DTFT在 [0,2π]区间的均匀采样，实 现频率离散化，可看作是 对频谱理论上的“采样”。
西安工业大学
3.3 离散傅里叶变换及其性质 五、DFT和离散时间信号的傅里叶变换
西安工业大学
3.0 引言
离散傅里叶变换和快速傅里叶变换
傅里叶分析方法要和计算机有效结合，需进行离散化，包 括时域的离散和频域的离散，离散傅里叶变换（Discrete Fourier Transform，DFT）正是解决这一问题，是一种便 于计算机实现的傅里叶变换。 快速傅里叶变换（Fast Fourier Transform，FFT）是DFT 的快速计算方法。1965年，J.W .Cooley和J.W .Tukey，在 《计算机数学》杂志（1965年第19卷）发表“机器计算傅 里叶级数的一种算法”，首先提出了FFT算法。FFT目前 在信号频谱分析、滤波器频率响应的计算、卷积运算、谱 估计算法及相关算法实现中都有很广泛的应用。
kn (k ) x (n)] X (n)WN DFS[ x n 0 N 1

离散序列的傅里叶变换

离散序列的傅里叶变换

离散序列的傅里叶变换离散序列的傅里叶变换傅里叶变换是信号处理中常用的一种工具，用于将时域中的信号转换为频域中的信号。

其中，连续信号的傅里叶变换已经广泛应用于科学和工程中，但对于离散信号的傅里叶变换，其应用价值也日益凸显。

离散傅里叶变换（DFT）是傅里叶变换的一种形式，适用于离散信号。

它是从连续傅里叶变换离散化而来的，将连续信号的傅里叶积分转换为离散信号的傅里叶级数展开。

其核心思想是将一个离散信号分解成一系列离散正弦和余弦信号的线性组合，以此来描述该离散信号的频域特性。

离散序列的傅里叶变换具体操作如下：1. 给定一个长度为N的离散序列x(n)。

2. 计算出该序列的离散时间傅里叶变换X(k)，其中k为频域中的离散频率。

3. 公式表示为：X(k)= ∑(N-1)n=0x(n)e^(-jk2πnk/N)其中，e代表自然对数的底数（即自然常数e）、j为虚数单位、k为离散的频率序列。

4. 对于每一个k（0≤k≤N-1），都可以得到一个相应的离散频谱值X(k)，其代表了该离散信号在频域中的属性。

5. 最后，可以将离散频谱绘制在频谱图上，以展示该信号的频谱特性。

离散傅里叶变换中存在一种名为快速傅里叶变换（FFT）的算法，可快速计算消耗计算量大的离散傅里叶变换。

FFT在信号处理领域中广泛应用，其速度远超普通的DFT算法，已成为信号处理中不可或缺的工具之一。

通过离散傅里叶变换，我们可以更加准确、详尽地分析和描述离散信号在频域中的特征。

同时，其在音频、光学、雷达等领域中都有广泛的应用，因此掌握离散傅里叶变换的原理和操作方法，对于信号处理工程师和科研工作者来说都是非常有益的。

总之，离散傅里叶变换作为一个重要的信号处理工具，对于科技发展和社会进步都具有重要的意义。

我们应该加强对其的研究，进一步挖掘其应用潜力，并将其运用于实际生产生活中。

离散傅里叶变换及其快速算法

离散傅里叶变换及其快速算法

ak 也是以 N周期的周期序列，满足 ak
~ X (k ) Nak
ak 。令 ln
（3.5）
将式（3.4）代入，得
N 1 j kn ~ ~ N X ( k ) x ( n )e n 0 2
k
（3.6）
~ X (k ) 式中， 是以N为周期的周期序列，称为
~ x (n) 的离散傅里叶级数，用DFS表示。
~(k )， N 相位为 幅度为 X
~ arg[ X (k )]
。
基波分量的频率为 2 N ，幅度为
~ 为arg[ X (1)]
~ X (1) N
，相位
。
x ( n ) 以 N 8 为周期 n) 【例3-1】设 x(n) R4 (，将
进行周期延拓，得到周期序列 幅频特性。
~ x ( n)
2016-12-8
解：根据定义求解

14 12 e 8e
j
j
2 k 6
10e
j
j
2 2k 6 j 2 5k 6
2 3k 6
6e
2 4k 6
10e
X (0) 60 X (3) 0
X (1) 9 j 3 3 X (4) 3 j 3
X (2) 3 j 3 X (5) 9 j 3 3
x 3(n )
当k取奇数（ k=2m+1 ，m=0，1，…， N/4-1 ）时
N n(2 m 1) X 1(2m 1) x 1(n ) x 1 n 4 W N 2 n 0 N 4 1 N n mn x 1(n ) x 1 n W W N N 4 4 n 0 2

第四章 离散傅里叶变换及其快速算法

第四章 离散傅里叶变换及其快速算法

离散 连续
周期延拓 非周期

4.1 离散傅里叶变换的定义
kn X (k ) DFT [ x(n)] x(n)WN , n 0 N 1 N 1 n 0 2 kn N
= x ( n )e
j
k=0, 1, , N-1
X ( k )WN kn k 0 N 1
1 x(n) IDFT [ X (k )] N 1 N
4 N
x D1X N
W N ( N 1 ) 2 ( N 1 ) WN W N ( N 1 )( N 1 ) 1
1
D
1 N
W N 2 ( N 1 )
1 DN N
dftmtx(N) 函数产生N×N的DFT矩阵DN conj(dftmtx(N))/N 函数产生N×N的IDFT矩阵DN-1
二、 圆周移位性质
1. 序列的圆周移位 x(n)的圆周移位定义为
y(n)=x((n+m))N RN(n) 其过程为: 1)、将x(n)以N为周期进行周期延拓得x((n))N 2)、将x((n))N左移m位，得x((n+m))N 3)、取其主值序列x((n+m))N RN(n) 循环移位过程如图所示
WNN 1

2 WN ( N 1)
WNN 1 2 WN ( N 1) ( WN N 1) ( N 1)
DFT
IDFT矩阵形式为
1 1 1 W 1 N 1 D 1 1 W N 2 N N 1 W N ( N 1 ) 1 W N 2 W
0 n N `1 0 k N `1
DFT 则： x1 (n) x2 (n) X1 ( K ) X 2 ( K )

【知识总结】快速傅里叶变换（FFT）

【知识总结】快速傅里叶变换（FFT）

【知识总结】快速傅⾥叶变换（FFT ）这可能是我第五次学FFT 了……菜哭qwq 先给出⼀些个⼈认为⾮常优秀的参考资料：快速傅⾥叶变换（FFT ）⽤于计算两个n 次多项式相乘，能把复杂度从朴素的O (n 2)优化到O (nlog 2n )。

⼀个常见的应⽤是计算⼤整数相乘。

本⽂中所有多项式默认x 为变量，其他字母均为常数。

所有⾓均为弧度制。

⼀、多项式的两种表⽰⽅法我们平时常⽤的表⽰⽅法称为“系数表⽰法”，即A (x )=n∑i =0a i x i上⾯那个式⼦也可以看作⼀个以x 为⾃变量的n 次函数。

⽤n +1个点可以确定⼀个n 次函数（⾃⾏脑补初中学习的⼆次函数）。

所以，给定n +1组x 和对应的A (x )，就可以求出原多项式。

⽤n +1个点表⽰⼀个n 次多项式的⽅式称为“点值表⽰法”。

在“点值表⽰法”中，两个多项式相乘是O (n )的。

因为对于同⼀个x ，把它代⼊A 和B 求值的结果之积就是把它带⼊多项式A ×B 求值的结果（这是多项式乘法的意义）。

所以把点值表⽰法下的两个多项式的n +1个点的值相乘即可求出两多项式之积的点值表⽰。

线性复杂度点值表⽰好哇好但是，把系数表⽰法转换成点值表⽰法需要对n +1个点求值，⽽每次求值是O (n )的，所以复杂度是O (n 2)。

把点值表⽰法转换成系数表⽰法据说也是O (n 2)的（然⽽我只会O (n 3)的⾼斯消元qwq ）。

所以暴⼒取点然后算还不如直接朴素算法相乘……但是有⼀种神奇的算法，通过取⼀些具有特殊性质的点可以把复杂度降到O (nlog 2n )。

⼆、单位根从现在开始，所有n 都默认是2的⾮负整数次幂，多项式次数为n −1。

应⽤时如果多项式次数不是2的⾮负整数次幂减1，可以加系数为0的项补齐。

先看⼀些预备知识：复数a +bi 可以看作平⾯直⾓坐标系上的点(a ,b )。

这个点到原点的距离称为模长，即√a 2+b 2；原点与(a ,b )所连的直线与实轴正半轴的夹⾓称为辐⾓，即sin −1ba 。

FFT变换相关公式IFFT变换(FFT逆变换)

FFT变换相关公式IFFT变换(FFT逆变换)

FFT变换相关公式IFFT变换（FFT逆变换）离散傅里叶变换（Discrete Fourier Transform, DFT）是信号处理中的一种重要技术，用于将一个离散序列（如时域信号）转换为频域表示。

而逆离散傅里叶变换（Inverse Discrete Fourier Transform, IDFT）则是将频域信号转换回时域表示。

在信号处理中，常用的FFT算法（快速傅里叶变换）是对DFT的一种高效实现，能够大大加快计算速度。

FFT算法利用了信号的周期性和对称性，将DFT的计算量从O(n^2)降低到O(nlogn)，其中n是信号的长度。

下面介绍一些与FFT和IFFT相关的公式和性质。

1.DFT公式：离散傅里叶变换的公式如下：X[k] = Σ(x[n] * exp(-i * 2π * k * n / N))其中，X[k]是频域信号的第k个频率分量，x[n]是时域信号的第n个采样点，N是信号的长度。

2.IDFT公式：逆离散傅里叶变换的公式如下：x[n] = (1/N) * Σ(X[k] * exp(i * 2π * k * n / N))其中，x[n]是逆变换后的时域信号，X[k]是频域信号的第k个频率分量，N是信号的长度。

3.FFT算法公式：FFT算法是一种将DFT计算量降低的方法，公式如下：X[k] = Σ(x[n] * W^(-kn))其中，W = exp(-i * 2π / N)是旋转因子，n和k分别表示时域和频域的索引。

4.IFFT算法公式：IFFT算法是FFT的逆变换，可以将频域信号转换为时域信号，公式如下：x[n] = (1/N) * Σ(X[k] * W^(kn))其中，W = exp(i * 2π / N)是旋转因子，n和k分别表示时域和频域的索引。

5.FFT和IFFT的性质：-线性性质：FFT和IFFT都满足线性性质，即对于多个信号的线性组合，其FFT和IFFT等于各自信号的FFT和IFFT的线性组合。

第三章离散傅里叶变换及其快速计算方法

第三章离散傅里叶变换及其快速计算方法

傅里叶系数标号k ：0～N
数字频率ω：0～2π 模拟频率 f ：0～fs
0
N /2
0
0
fs /2
0
s /2
北京邮电大学信息与通信工程学院
N k (变换系数标号) 2 （弧度，数字频率） fs f （Hz，模拟频率） s （弧度/秒，模拟角频率）
24
DFS 定义：几点说明
频率成份
直流分量：
N 1
北京邮电大学信息与通信工程学院
11
DFS 定义：预备知识
基本关系式 若 r，m 都是整数,则:
N N 1 j 2 k(r m )
eN
k0
0
rm rm
证明: 对于r=m：不论 k 取何值，显然等式成立。
对于r≠m：
1 W N 1 j 2 k(rm) N
e W 1W k0
N 1 k(rm)
离散傅里叶级数包含了 0 到 (N-1)fs/N 的频率，因而 N 个傅里叶级数的系 数位于从 0 直到接近取样频率的频率上。
N 1
当 k=0 时， X (0) x(n)WN 0n x(n) ，此时得到的傅里叶级数的系数
称为信号的直流分量（DnC0 Componenn0t）X，(0)/ N 是信号的平均值；
交流分量：
其它频率（k>0）称为周期信号的谐波，此时的傅里叶级数系数称为 信号的交流分量。
k=1 时的频率为信号的一次谐波，或基频，频率大小为 fs/N，时间为 NTs，等于完成一个周期所需要的时间。其它谐波为基频的整数倍。
8
3.1 问题的提出：傅里叶变换的四种形式 （6）
四种傅里叶变换形式的归纳总结：
形式
时间函数
频率函数

第3章1-4 离散傅里叶变换及其快速算法讲解

第3章1-4 离散傅里叶变换及其快速算法讲解

考虑到DFT关系的对偶性，可以证明，长为N的两序列之积的DFT 等于它们的DFT的循环卷积除以N，即
3种卷积： 线性卷积 线性卷积不受主值区间限制 周期卷积 循环卷积 是周期卷积取主值，在一定条件下与线性卷积相等。 两个长度都为N的因果序列的循环卷积仍是一个长度为N的序列， 而它们的线性卷积却是一个长度为2N-1的序列。
设x1(n)和x2(n)都是长度为N的有限长因果序列，它们的线性卷 积为
它是长为2N-1的序列。
现将x1(n)和x2(n)延长至L(L>N)，延长部分(从N到L-1)均填充为零 值，计算x1(n)和x2(n)的L点循环卷积，得到
为了下面分析方便，先将x1(n)和x2(n)以L为周期进行延拓，得 到两个周期序列
若它们长度不等，取长度最大者，将短的序列通过补零加长，注 意此时DFT与未补零的DFT不相等。
此性质可以直接由DFT的定义进行证明。
2．对称性 最常遇到的是实序列。设x(n)是一个长度为N的实序列，且
DFT[x(n)]=X(k)，则有 这意味着
或
这就是说，实序列的DFT系数X(k)的模是偶对称序列，辐角是 奇对称序列。
何信息。这正是傅里叶变换中时域和频域对偶关系的反映，这有 着十分重要的意 义。DFT实现了频域离散化，开辟了在频域采用 数字技术处理的新领域。
这使我们自然想到，对于任意一个频率特性，是否均能用频域
采样的办法来逼近，这是一个很吸引人的问题，因为用频率采样 来逼近，可使问题大大简化。因此我们要讨论频率采样的可行性 以及所带来的误差。
Matlab实现 fft1.m
X(4)=0.46235 X(5)= 0.47017+j0.16987 X(6)= 0.50746+j0.40597 X(7)= 0.71063+j0.92558

第三章 离散傅里叶变换(DFT)及其快速算法(FFT)2

第三章 离散傅里叶变换(DFT)及其快速算法(FFT)2

由8点DIT-FFT运算流图可以发现，第L级共有2L-1个 不同的旋转因子。 N=23=8时的各级旋转因子表示如下: 0 L=1时 WNp WN
L=2时 L=3时
0 2 WNp WN , WNp WN
0 1 2 3 WNp WN ,WNp WN ,WNp WN ,WNp WN
倒 二进制数 0 0 1 1 0 0 1 1 0 0 0 0 1 1 1 1
序 十进制数 J 0 4 2 6 1 5 3 7
X (0), X (1), X (2), X (7)
12
由8点DIT-FFT运算流图可见，N=2M时，其DIT-FFT运算流图 由M级蝶形构成，每级有N/2个蝶形。因此，每级需要N/2 次复数乘法运算和N次复数加法运算，M级蝶形所需复数乘 法次数CM(2)和复数加法次数CA(2)分别为
CM (2) N N M log2 N 2 2
CA (2) NM N log 2 N
N=2M点的FFT共进行M级运算，每级由N/2个蝶形运算组成。同一级中，每个 蝶形的两个输入数据只对计算本蝶形有用，而且每个蝶形的输入、输出数 据节点又同在一条水平线上，这就意味着计算完一个蝶形后，所得输出数 据可立即存入原输入数据所占用的存储单元。这样，经过M级运算后，原 来存放输入序列数据的N个存储单元(A(0),A(1),…,A(N-1))中便依次存放 X(k)的N个值。这种利用同一存储单元存储蝶形计算输入、输出数据的方 法称为原位（址）计算。 • 节约内存单元，降低设备成本
0 WN 0 WN 0 WN
2 WN
X (0) X (1) X (2) X (3) X (4) X (5) X (6) X (7)
20
W N0
0 WN 0 WN 0 WN

数字信号处理第三章离散傅里叶变换(DFT)及其快速算法(FFT)

数字信号处理第三章离散傅里叶变换(DFT)及其快速算法(FFT)

周期
2
s、fs N
分辨率
2
N
fs N
返回
回到本节
DFT和DFS之间的关系：
周期延拓
取主值
有限长序列
周期序列
主值区序列
有限长序列 x(n) n 0,1, 2, M 1

周期序列 xN (n) x(n mN ) x((n))N m 0 n0 N 1 n mN n0 ((n))N n0
四种傅立叶变换
离散傅立叶变换（DFT）实现了信号首次在频域 表示的离散化，使得频域也能够用计算机进行处理。 并且这种DFT变换可以有多种实用的快速算法。使信 号处理在时、频域的处理和转换均可离散化和快速 化。因而具有重要的理论意义和应用价值，是本课程 学习的一大重点。
本节主要介绍
3.1.1 DFT定义 3.1.2 DFT与ZT、FT、DFS的关系 3.1.3 DFT的矩阵表示
• X(k)为x(n)的傅立叶变换 X (e j ) 在区间 [0, 2 ]上的N
点等间隔采样。这就是DFT的物理意义。
j ImZ
2பைடு நூலகம்3
4
5 6
1 2
N
k=0 ReZ
7 (N-1)
DFT与z变换
X(ejω)
X(k)
0
o

2
0
N 1 k
DFT与DTFT变换
回到本节
变量

、f k
之间的某种变换关系.
• 所以“时间”或“频率”取连续还是离 散值,就形成各种不同形式的傅里叶变换 对。
3.1 离散傅里叶变换的定义及物理意义
时间域
t:连续
模拟域

fft计算公式

fft计算公式

快速傅里叶变换（FFT）是一种计算离散傅里叶变换（DFT）及其逆变换的高效算法。

FFT的计算公式如下：
X[k] = ∑(n=0 to N-1) x[n] * W[k*n]
其中，X[k]表示离散傅里叶变换的输出，x[n]表示输入的时域信号，N表示输入信号的采样点数，W[k*n]表示复数单位元，即W[k*n] = e^(-2πikn/N)。

对于逆变换，可以使用以下公式：
x[n] = ∑(k=0 to N-1) X[k] * W[-k*n] / N
其中，x[n]表示输入的时域信号，X[k]表示离散傅里叶变换的输出，N表示输入信号的采样点数，W[-k*n]表示复数单位元的逆变换。

这些公式可以根据实际需求进行适当的修改和扩展，例如对于实数信号可以省略虚部，对于对称性可以优化计算等。

功率谱 频谱计算

功率谱 频谱计算

功率谱频谱计算摘要：一、引言二、功率谱和频谱的概念1.功率谱2.频谱三、功率谱和频谱的计算方法1.离散傅里叶变换（DFT）2.快速傅里叶变换（FFT）四、功率谱和频谱在实际应用中的意义1.在信号处理中的应用2.在通信系统中的应用五、总结正文：一、引言在信号处理和通信系统中，功率谱和频谱的计算是非常重要的。

它们可以帮助我们更好地分析和理解信号的特性。

本文将详细介绍功率谱和频谱的概念，以及它们的计算方法。

二、功率谱和频谱的概念1.功率谱功率谱是一种描述信号能量分布的函数，它反映了信号在不同频率下的能量大小。

功率谱通常用一个矩形图表示，横轴是频率，纵轴是信号的功率。

2.频谱频谱是信号在频域中的表示形式，它显示了信号在不同频率下的振幅和相位信息。

频谱通常用一个波形图表示，横轴是频率，纵轴是信号的振幅或相位。

三、功率谱和频谱的计算方法1.离散傅里叶变换（DFT）离散傅里叶变换是一种将时域信号转换为频域信号的算法。

它通过将信号分解成一组正弦和余弦函数的叠加，从而得到信号的频谱。

2.快速傅里叶变换（FFT）快速傅里叶变换是离散傅里叶变换的快速算法。

它利用信号的对称性和周期性，将DFT 的计算复杂度从O(N^2) 降低到O(NlogN)。

四、功率谱和频谱在实际应用中的意义1.在信号处理中的应用功率谱和频谱在信号处理中被广泛应用，如滤波、信号识别、噪声抑制等。

通过分析信号的频谱，我们可以了解信号的频率成分，从而对信号进行适当的处理。

2.在通信系统中的应用在通信系统中，功率谱和频谱的计算对于信号调制和解调、信道估计、误码纠正等环节至关重要。

准确的功率谱和频谱分析可以提高通信系统的性能和可靠性。

五、总结本文介绍了功率谱和频谱的概念，以及它们的计算方法。

通过这些方法，我们可以更好地分析和理解信号的特性。

离散傅里叶变换及快速算法

离散傅里叶变换及快速算法

序列分解为N个谐波相关的复指数之和。将
j 2N nk
X (k ) x(n)e
, k 0,1,2,
（5-3）
称之为离散傅里叶级数DFS的k次谐波系数。是一个基波周 期为N的周期序列。
X (k ) X ( k N )
§5．离散傅里叶变换及快速算法
在DFS变换中引入复数
k
X ( jk0 )e jk0t
*时域周期为Tp, 频域谱线间隔为2π/Tp
时域信号 连续的 周期的
频域信号
非周期的
离散的
3.离散时间、连续频率的傅立叶变换 – DTFT（离散时间傅立叶 变换） X e 或 X (e ) x(nT) T
j jT
---T 0 T 2T
正 : X (e
WN e
j 2N
将DFS正反变换描述为
nk 正 : X (k ) DFSx (n) X (k ) x (n)WN n 0
N 1
1 N 1 反 : x (n) IDFS X (k ) x (n) X (k )WN nk N k 0


（5-5）
WN
的性质: 1 N 1 ( nm) k 1 n m lN 正交性: WN 0 n m lN N k 0
周期性:
W
k mN N
W
k N
l , m, N / 2, k / 2均为整数
共轭对称性（偶序列）: 可约性：
k N (WN )* WN k
k mk k 2 WN WmN WN // 2
§5．离散傅里叶变换及快速算法
2.离散傅里叶变换（DFT）
但对于数字系统，无论是Z 变换还是序列傅立叶变换的适用方面都存 在一些问题，重要是因为频率变量的连续性性质（DTFT变换出连续频 谱），不便于数字运算和储存。 参考DFS，可以采用类似DFS的分析方法解决以上问题。可以把有限 长非周期序列假设为一无限长周期序列的一个主值周期，即对有限长非 周期序列进行周期延拓，延拓后的序列完全可以采用DFS进行处理，即 采用复指数基频序列和此有限长时间序列取相关，得出每个主值在各频 率上的频谱分量以表示出这个“主值周期”的频谱信息。 由于DFT借用了DFS，这样就假设了序列的周期无限性，但在处理时 又对区间作出限定（主值区间），以符合有限长的特点，这就使DFT带 有了周期性。另外，DFT只是对一周期内的有限个离散频率的表示，所 以它在频率上是离散的，就相当于DTFT变换成连续频谱后再对其采样， 此时采样频率等于序列延拓后的 周期N，即主值序列的个数。

离散傅里叶变换和快速傅里叶变换

离散傅里叶变换和快速傅里叶变换

戶幵,戈丿、弟实验报告课程名称：彳_____________ 指导老师 _____________ 成绩： ____________________实验名称：离散傅里叶变换和快速傅里叶变换 实验类型: _________________ 同组学生姓名：一、实验目的和要求(必填) 二、实验内容和原理(必填) 三、主要仪器设备(必填) 四、操作方法和实验步骤 五、实验数据记录和处理 六、实验结果与分析(必填)七、讨论、心得一、实验目的和要求1. 掌握DFT 的原理和实现2.掌握FFT 的原理和实现，掌握用FFT 对连续信号和离散信号进行谱分析的方法。

二、实验内容和原理2.1 DTFT 和 DFTN 1如果x(n)为因果有限长序列,n=0,1,...,N-1，则x(n)的DTFT 表示为：X(e j ) x(n)en 0序列的N 点DFT 是DTFT 在［0,2 n 上的N 点等间隔采样，采样间隔为2 d N 。

通过DFT , 可以完成由一组有限个信号采样值x(n)直接计算得到一组有限个频谱采样值X(k)。

X(k)的幅度谱为X(k) v 'x R (k ) X |2(k ) , X R (k)和X i (k)分别为X(k)的实部和虚部。

X(k)的相位谱 为(k)列吩序列x(n)的离散事件傅里叶变换(DTFT )表示为:X(e j )x( n)ex(n)的离散傅里叶变换(DFT )表达式为:X(k)x(n)en 0j^nk N(k 0,1,…,N 1)IDFT )定义为 x(n)丄 N \(k)e j_Nnk (n 0,1，…，N 1)N n 02.2 FFT快速傅里叶变换(FFT )是DFT 的快速算法，它减少了 DFT 的运算量，使数字信号的处理速度大大提高。

三、主要仪器设备PC 一台，matlab 软件四、实验内容4.1第一题x(n)的离散时间 傅里叶变换(DTFT ) X(e j Q)并绘图。

  1. 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
  2. 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
  3. 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

戶幵,戈丿、弟实验报告课程名称：彳_____________ 指导老师 _____________ 成绩： ____________________实验名称：离散傅里叶变换和快速傅里叶变换 实验类型: _________________ 同组学生姓名：一、实验目的和要求(必填) 二、实验内容和原理(必填) 三、主要仪器设备(必填) 四、操作方法和实验步骤 五、实验数据记录和处理 六、实验结果与分析(必填)七、讨论、心得一、实验目的和要求1. 掌握DFT 的原理和实现2.掌握FFT 的原理和实现，掌握用FFT 对连续信号和离散信号进行谱分析的方法。

二、实验内容和原理2.1 DTFT 和 DFTN 1如果x(n)为因果有限长序列,n=0,1,...,N-1，则x(n)的DTFT 表示为：X(e j) x(n)en 0序列的N 点DFT 是DTFT 在［0,2 n 上的N 点等间隔采样，采样间隔为2 d N 。

通过DFT , 可以完成由一组有限个信号采样值x(n)直接计算得到一组有限个频谱采样值 X(k)。

X(k)的幅度谱为X(k) v 'x R (k )X |2(k ), X R (k)和X i (k)分别为X(k)的实部和虚部。

X(k)的相位谱 为(k)列吩序列x(n)的离散事件傅里叶变换(DTFT )表示为:X(e j)x( n)ex(n)的离散傅里叶变换(DFT )表达式为:X(k)x(n)e n 0j^nk N(k 0,1,…,N 1)IDFT )定义为 x(n)丄 N \(k)ej_Nnk(n 0,1，…，N 1)N n 02.2 FFT快速傅里叶变换(FFT )是DFT 的快速算法，它减少了 DFT 的运算量，使数字信号的处理速度大大提高。

三、主要仪器设备PC 一台，matlab 软件四、实验内容4.1第一题x(n)的离散时间 傅里叶变换(DTFT ) X(e j Q)并绘图。

0 其2他n 2; (2)已知 x(n) 2n 0 n 10。

0其他4.1.1理论分析1)由DTFT 计算式,X (Q)是实数，可以直接作出它的图像。

离散傅里叶反变换求有限长离散时间信号(1)已知 x(n)X( ) x(n)e jne 2j1 5je1 e je 2® e 2®0.5j e0.5 jesin(2.5 )2)由DTFT计算式:Figure 1 X (Q)曲线X( x(n)e j io2n e jn 01夕1©11」1 2e jz11111 2e jX(211 1 2e j可以发现(Q)周期为2 n;而X (Q)的相位在2n周期内有约十次振荡。

4.1.2编程计算作图编写一个计算DTFT的函数。

fun cti on DTFT(x, n1,n2) w=-2*pi:2*pi/1000:2*pi; % X=zeros(size(w));for i=n 1: n2 %DTFT表示Q 计算式X=X+x(i-n1+1)*exp((-1)*j*w*i);endan gle(X);subplot(2,1,1);plot(w, abs(X), 'r');xlabel( '\Omega' );ylabel( subplot(2,1,2);plot(w,a ngle(X), 'b');xlabel( '\Omega' );ylabel( end'|X(\Omega)|' );hold on; % 作幅频图'\an gle(\Omega)' ); % 作相频图输入序列x,和n的取值范围，即可计算其DTFT。

1) 输入：x=[1 1 1 1 1]; DTFT(x,-2,2);(因为X (Q)是实数，所以实际计算过程中对相频曲线取了绝对值) 结果：2) 输入：n=0:10; x=2.An;DTFT(x,0,10)结果:2500200015001000-10 -5 0 5 0Figure 3第1题(2)中X (Q )的频谱500-1Figure 2 X (Q)的频谱可以看出，X (Q)的相位只有 0和n 两种取值，X (Q)是实函数，而且其幅度频谱 与理论计算得到的相同。

4.2第二题已知有限长序列x(n)={色7,9,5,1,7,9,5},试分别采用DFT和FFT求其离散傅里叶变换X(k)的幅度、相位图。

4.2.1理论分析由FFT 蝶形运算得到，X(k)= 51,7,-9-j4,7,3,7,-9+j4,74.2.2编程计算作图1. DFT编写一个计算DTFT的函数。

DFT (序列x，长度N )fun ctio n DFT(x,N)k=0:N-1;X=zeros(size(k));for n=0:N-1X=X+x( n+1)*exp((-1)*j*2*pi/N* n*k); %DFT计算式endsubplot(2,1,1);stem(k,abs(X), '.' ); xlabel( 'k' );ylabel( '|X(k)|' );hold on; %幅频图subplot(2,1,2);stem(k,angle(X), '*' );xlabel( 'k' );ylabel( 'Angle(k)' ); %相频图end输入：x=[8 7 9 5 1 7 9 5];DFT(X,8);结果：Figure 4 第2题DFT结果2. FFT编写一个利用matlab自带函数计算FFT并绘图的函数FFT1 (序列x，长度N)fun cti on FFT1(x,N)X=fft(x,8); %用自带的fft函数计算k=0:N-1;subplot(2,1,1);stem(k,abs(X), '.' ); xlabel( 'k' );ylabel( '|X(k)|' );hold on; %幅频图subplot(2,1,2);stem(k,angle(X), '*' );xlabel( 'k' );ylabel( 'Angle(k)' ); %相目频图end输入：x=[8 7 9 5 1 7 9 5];FFT1(X,8);结果：Figure 5 第2题FFT结果因为FFT只是DFT的一种快速算法，所以FFT的结果与DFT结果相同。

DFT和FFT的结果，符合理论计算得到的，X(k)= 51,7,-9-j4,7,3,7,-9+j4,74.3第三题已知连续时间信号x(t)=3cos8 n t, X( 3 )= 3 [ ( 8 ) ( 8 )]，该信号从t=0开始以采样周期Ts=0.1 s进行采样得到序列x(n)，试选择合适的采样点数，分别采用DFT和FFT 求其离散傅里叶变换X(k)的幅度、相位图，并将结果与X(k)的幅度、相位图，并将结果与X( 3 )相比较。

4.3.1理论分析1.原信号的频谱：X( 3 )=3 [ ( 8 ) ( 8 )],只在土8n不为0.且在土8n处相2.采样角频率Q S=20 n> 2 X 8 n,满足采样定理。

3.采样后的信号，为X( 3 )以20 n为周期的延拓。

所以只在(土8+20k )n ( k为任意整数)处不为0.如取区间［0,20 n ］内，只有8n和16 n处不为0。

进行N点DFT后，将8 1220 n的区间映射为［0,N］区间。

理想情况下仅在n= N和N两处不为0。

20 204.x(n) cos(8 nTs) cos(0.8 n)，周期为5,所以取采样点数为5的倍数时，不会发生泄漏；而采样点数不是5的倍数时，则会发生泄漏。

1013 3 1 1 1 1 3 19-876■)X 543141Figure 6原始信号的频谱X (Q)4.3.2编程计算作图编写一个获得信号的N点样本的函数sample (点数N)fun cti on x=sample(N)t=0:0.1:(N-1)*0.1; %0.1s 为间隔x=3*cos(8*pi*t); %x 即采样结果End输入：X=sample(N);FFT1(X,N);即可获得采样N点的频谱图。

因为DFT结果与FFT是完全一样的，所以这里只使用FFT 作图。

取采样点数N=5 16 20 104获得以下频谱图：• • •■■■--. o5 1J \ 2.51 3 3.5Figure 7 N=5 Figure 8 N=16 Figure 9 N=2080Figure 10 N=104可以看出，N=5和20时，由于是周期的整数倍，频谱只有两条谱线，且满足前面8 12理论计算得出的公式n= —N和宜 N，没有发生泄漏，且这两条谱线对应20 20的相位是0.所以频谱与原信号频谱在形式上时相同的。

而N=16和N=54时，则都发生了频谱泄漏，频谱与原信号频谱就很不同了。

但相比之下N=54时谱线更加接近原谱线。

验证了“为减小泄漏误差，如果待分析的信号实现不知道确切周期，则截取较长时间长度的样点进行分析”这个说法。

同时也可以发现，虽然幅频图中显示幅值为0，但相频图中相应的位置仍有谱线。

这可能是matlab浮点运算造成的误差，即本来为0处其实是一个非常小的复数，所以仍有一定相位。

4.4第四题4.4.1理论分析若噪声信号较小，则采样后的频谱仍能较准确地反映原信号的特征。

4.4.2编程计算对原采样程序稍加改编，加入一个噪声信号p*randn(1,N)。

p表示噪声信号的强度。

fun cti on x=sample no ise(N,p)t=0:0.1:(N-1)*0.1;x=3*cos(8*pi*t)+p*ra ndn (1,N);end取采样点数N=20进行分析。

输入：X=samplenoise(20,p); % 取P=1 和 10 两种情况。

难准确获得原信号的频谱。

4.5第五题(n 3)，X(k)是 x(n)的 6 点 DFT ,设(1)若有限长序列y(n)的6点DFT 是Y(k) W 64k X(k)，求y(n)。

可见，较小的噪声对信号的频谱的影响不大,仍能较精确地获得频谱图。

而噪声较大时则很 3.5 已知序列 x(n) 4 (n) 3 (n 1) 2 (n 2) FFT1(X,20);30 Figure 11N=20 噪声较小(p=1 ) -0 2 4 6 8 10 12 14 16 18 20 k -2 A 4 2 1 0 -2 20 e g A Figure 12N=20 噪声较大(p=10 ) -4 I _____ I _____ I _______ I _____ [ _____ [ ______ I ____ I ______ I _____ l_ 0 2 4 6 8 10 12 14 16 18 k(2) 若有限长序列 w(n)的6点DFT W(k)是X (k)的实部，求w(n)。