多元函数的连续性
二元函数的连续性
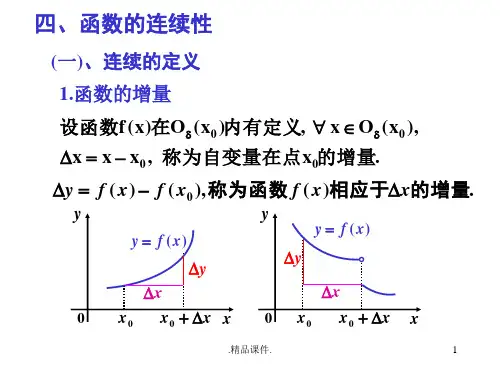
定义1()(,)D f P f x y =设二元函数的定义域为，
00000,)D ,)D P x y P x y ∈（是的聚点，且（
，如果0000,)(,)
lim (,)(,)x y x y f x y f x y →=（00(,)(,)f x y P x y 则称函数在点处连续。
(,)D (,)D (,)D (,)C()
f x y f x y f x y f x y D ∈如果在的每一点处都连续，则称函数在上连续，或称是上的连续函数，记作
例1讨论函数222,(,)(0,0)(,)0,(,)(0,0)x y x y f x y x y
x y ?≠?=+??=?
在(0,0)处的连续性．
解2
22x y x y +x 2
1≤,00??→?→x 222
00
lim 0(0,0)x y x y f x y →→∴==+故函数在(0,0)处连续.
例2讨论函数
??
??
?=+≠++=0,00,),(222222y x y x y x xy y x f 在(0,0)的连续性．
解取kx
y =2222
0lim x k x kx kx
y x +==→21k k +=其值随k 的不同而变化，极限不存在．故函数在(0,0)处不连续．
闭区域上连续函数的性质
（1）最大值和最小值定理
有界闭区域D上的多元连续函数一定有最大值和最小值．
（2）介值定理
在有界闭区域D上的多元连续函数必取得介于最大值和最小值之间的一切值．
多元初等函数：由多元多项式及基本初等函数经过有限次的四则运算和复合步骤所构成的可用一个式子所表示的多元函数叫多元初等函数一切多元初等函数在其定义区域内是连续的．
定义区域是指包含在定义域内的区域或闭区域．
设n 元函数)(P f 的定义域为点集0,P D 是其聚点且D P ∈0，如果)()(lim 00P f P f P P =→则称n 元函数)(P f 在点0P 处连续. 设0P 是函数)(P f 的定义域的聚点，如果)(P f 在点0P 处不连续，则称0P 是函数)(P f 的间断点.
多元函数的连续性
定义1
小结
1.二元函数连续的定义,性质
2.n元函数连续的定义
目录 摘要 (1) 关键词 (1) Abstract (1) Key words (1) 引言 (1) 1二元函数连续、偏导数、可微三个概念的定义 (1) 2二元函数连续、偏导数、可微三个概念之间的关系 (2) 2.1二元函数连续与偏导数存在之间的关系 (2) 2.2二元函数连续与可微之间的关系 (3) 2.3二元函数可微与偏导数存在之间的关系 (3) 2.4二元函数可微与偏导数连续之间的关系 (4) 二元函数连续、偏导数、可微的关系图 (6) 参考文献 (7) 致谢 (8)
本科生毕业论文 2 二元函数的连续、偏导数、可微之间的关系 摘要 一元函数可微与可导等价，可导必连续.但二元函数并非如此，以下文章给出了二元函数连续、偏导数、可微之间的关系，并给出了简单的证明，且用实例说明了它们之间的无关性和在一定条件下所具有的共性. 关键词 二元函数 连续 偏导数 可微 The Relationship among Continuation, Partial Derivatives and Differentiability in Binary Function Abstract Unary function differentiable with derivative equivalent, will be continuously differentiable. But the dual function is not the case, the following article gives a continuous function of two variables, partial derivatives, can be said the relationship between them, and gives a simple show, and illustrated with examples related between them and under certain conditions have in common.. Key words binary function continuation partial derivatives differentiability 引言 二元函数的偏导数存在、函数连续、可微是二元函数微分学的三个重要概念.对于学习数学分析的人来说，必须弄清三者之间的关系，才能学好、掌握与之相关的理论知识.本文详细讨论这三者之间的关系. 1 二元函数连续、偏导数、可微三个概念的定义 定义1 设f 为定义在点集2D R ?上的二元函数，0D P ∈（0P 或者是D 的聚点，或者是D 的孤立点），对于任给的正数ε，总存在相应的正数δ，只要0,)(D P U P δ?∈， 就有0)||()(f P f P ε<-，则称f 关于集合 D 在点0P 连续. 定义2 设函数(,),(,)z f x y x y D =∈，若00,)(y D x ∈且0,)(y f x 在0x 的某一邻域内 有定义，则当极限00000000(,))(,) (,lim lim x x x f x y f x y f x x y x x ?→?→+-=????存在时，则称这个极限 为函数f 在点00,)(y x 关于x 的偏导数，记作0 (,) |x y f x ??. 定义3 设函数(,)z f x y =在点000,)(y P x 某邻域0()U P 内有定义， 对于0()U P 中的点00,)(,)(y P x y x x y ++=??，若函数f 在点0P 处的全增量可表示为
多元函数的极限与连续习题 1. 用极限定义证明:14)23(lim 1 2=+→→y x y x 。 2. 讨论下列函数在（0,0）处的两个累次极限，并讨论在该点处的二重极限的存在性。 （1）y x y x y x f +-=),(； (2) y x y x y x f 1sin 1sin )(),(+=； (3) y x y x y x f ++=23 3),(； (4) x y y x f 1 sin ),(=。 3. 求极限 （1）2 20 ) (lim 22 y x x y x y +→→； （2）1 1lim 2 2 220 0-+++→→y x y x y x ； （3）2 20 01 sin )(lim y x y x y x ++→→； （4）22220 0) sin(lim y x y x y x ++→→。 4. 试证明函数?? ???=≠+=0 0)1ln(),(x y x x xy y x f 在其定义域上是连续的。
1. 用极限定义证明:14)23(lim 2 1 2=+→→y x y x 。 因为1,2→→y x ，不妨设0|1|,0|2|<-<-y x ， 有54|2||42||2|<+-≤+-=+x x x ， |22123||1423|2 2 -+-=-+y x y x |1|2|2|15|1|2|2||2|3-+-<-++-≤y x y x x |]1||2[|15-+-
一、引言 对于一元函数而言,函数y=f(x在点x0处连续、导数存在、可微这三个概念的关系是很清楚的,即可微一定连续,但连续不一定可微,可微和导数存在是等价的。对多元函数而言,由于偏导数的出现,使得他们之间的关系要复杂的多。下面以二元函数为例,探讨其在点(x0,y0处连续、偏导数存在、可微、偏导数连续之间的关系。 二、二元函数连续、偏导数存在、可微、偏导数连续之间的关系 1.可微与连续的关系 若函数f(x,y在点(x0,y0处可微,则在该点连续,但反之不成立(同一元函数。 证明:因为f(x,y在点(x0,y0处可微,因此有0≤f(x0+△x,y0+△y- f(x0,y0≤A△x+B△y+O(O→(△x→0,△y→0, 所以lim (△x,△y→(0,0 f(x0+△x,y0+△y=f(x0,y0,故f(x,y在 点(x0,y0处连续。反之不成立。 例1.f(x,y= x2y x2+y2 ,x2+y2≠0 0,x2+y2= $
在点(0,0处连续, 但在该点不可微。 2.偏导数存在与可微的关系 由定理17.1[1](可微的必要条件,函数f(x,y在点(x0,y0处可微,则f(x,y在点 (x0,y0的偏导数一定存在;但反之不成立,如例1中函数f(x,y在点(0,0处偏导数存在,但在此点不可微。 3.偏导数连续与可微的关系 由定理17.2[2](可微的充分条件知,函数f(x,y在点(x0,y0处偏导数连续,则f(x,y 在点(x0,y0处可微;但反之不成立, 例2.f(x,y=(x2+y2sin1 x2+y2 ,x2+y2≠0 0,x2+y2= % ’ ’ ’ & ’ ’
讨论多元函数连续、偏导数存在、可微之间的关系 祁丽梅 学院数学与统计学院 ， 024000 摘要: 本文先是对二元函数连续性、偏导数存在及可微之间的关系就具体实例进行了讨论，然后推广到多元函数由此来总结有关多元函数微分学中关于上述三个概念之间的关系，并通过二元函数具体的实例详细加以证明。 关键词: 二元函数；多元函数；连续；偏导数；存在；可微 一、引言 多元函数微分学是数学学习中的重要容,是微积分学在多元函数中的具体体现，多元函数的连续性，偏导数存在及可微性之间的关系是学生在数学学习中易发生的概念模糊和难以把握的重要知识点。尽管它与一元函数的微分学有许多共同点，但它们之间也同样有一些差异，这些差异是由“多元”这一特殊性引起的。 二、二元函数连续、偏导数存在、可微之间的关系 1、若二元函数f 在其定义域某点可微，则二元函数f 在该点偏导数存在，反过来则不一定成立。 可微的必要条件： 若二元函数在()000,y x p 可微，则二元函数()y x f z ,=在()000,y x p 存在两个偏导数，且全微分 y B x A dz ?+?=中的A 与B 分别是()00,y x f A x '=与()00,y x f B y '= 其中y x ??,为变量y x ,的改变量，则dy y dx x =?=?,，于是 二元函数的全微分为()()dy y x f dx y x f dz y x 0000,,'+'= 类似的n 元函数()n x x x f u ,,,21 =在点()n x x x Q ,,,21 的全微分为 n n dx x f dx x f dx x f dx x f du ??++??+??+??= 222211 我们知道一元函数的可微与可导是等价的，但通过上述情况可以知道二元函数可微一定存在两
§5.1 多元函数的概念、极限与连续性 一、多元函数的概念 1. 二元函数的定义及其几何意义 设D 是平面上的一个点集，如果对每个点()p x y D ∈，，按照某一对应规则f ，变量z 都有一个值与之对应，则称z 是变量x y ，的二元函数，记以()z f x y =，，D 称为定义域。 二元函数()z f x y =，的图形为空间一块曲面，它在xy 平面上的投影区域就是定义域D 。 例如 22: 1z D x y =+≤二元函数的图形为以原点为球心，半径为1 的上半球面，其定义域D 就是xy 平面上以原点为圆心， 半径为1的闭圆。 2. 三元函数与n 元函数。 ()()u f x y z x y z =∈ΩΩ，，，，，，为空间一个点 集则称()u f x y z =，，为三元函数 ()12n u f x x x =，，，，称为n 元函数。 它们的几何意义不再讨论，在偏导数和全微分中会用到三元函数。条件极值中，可能会遇到超过三个自变量的多元函数。 【例1】 求函数arcsin 3 x z = 解 要求13 x ≤，即33x -≤≤； 又要求0xy ≥即00x y ≥≥，或00x y ≤≤， 综合上述要求得定义域300x y -≤≤??≤?或030 x y ≤≤??≥?
【例2】 求函数()2ln 21z y x =-+的定义域。 解 要求2240x y --≥和2210y x -+> 即 2222212x y y x ?+≤??+>?? 函数定义域D 在圆2222x y +≤的内部 （包括边界）和抛物线212y x +=的左侧（不包括抛物线上的点） 【例3】 设()22 f x y x y x y y +-=+，，求()f x y ，。 解 设x y u x y v +=-=，解出()()1122 x u v y u v = +=-， 代入所给函数化简 ()()()()221184 f u v u v u v u v +-+-，＝ 故 ()()()()221184f x y x y x y x y +-+-，＝ 【例4】 设()22 35f x y xy x xy y ++++，＝，求()f x y ，。 解 ()22223525x xy y x xy y xy +++=++++ ()25x y xy =+++ ∴ ()25f x y x y =++， 二、 二元函数的极限 设()f x y ，在点()00x y ，的去心邻域内有定义；如果对任意0ε>，存在0δ>，只要 0δ<，就有()f x y A ε-<， 则记以()00lim x x y y f x y A →→=，或()() ()00lim x y x y f x y A →=，，， 称当()x y ，趋于()00x y ，时，()f x y ，的极限存在，极限值为A ，否则，称为极限不存在.
§3 二元函数的连续性 (一) 教学目的： 掌握二元函数的连续性的定义，以及多元函数的局部性质和它们在有界闭域上的整体性质． (二) 教学内容：二元函数的连续性的定义；有界闭域上连续函数的有界性，最大最小值定 理，介值性定理和一致连续性． 基本要求： (1) 掌握二元函数的连续性的定义，了解有界闭域上连续函数的性质． (2) 较高要求：掌握有界闭域上连续函数性质的证明要点． (三) 教学建议： (1) 有界闭域上多元连续函数的性质基本上与一元函数的情况类似，教学中可通过复习一元连续函数的定理引出．对较好学生，可布置一些与有界闭域上多元连续函数的性质有关的习题 —————————————————————— 一． 二元函数的连续概念 由一元函数连续概念引入 . 定义（用“δε-”定义二元函数连续） 设函数),(y x f 为定义在点集2R D ?上的二元函数，D P ∈0（它或者是D 的聚点，或者是D 的孤立点），若对0,0>?>?δε，使 得当 D P U P );(0δ∈时，都有 ε<-|)()(|0P f P f 则称),(y x f 关于集合D 在0P 点连续，简称0P f 在点连续。 若函数D f 在上任何点都连续，则称D f 为上的连续函数。 由连续定义，若0P 是D 的孤立点，则0P 必定是f 关于集合D 的连续点；若0P 是D 的聚点，则f 关于集合D 在0P 连续等价于 )()(lim 00 P f P f D P P P =∈→ 如果0P 是D 的聚点，而上式不成立，则称f 关于集合D 在0P 不连续（或间断点）。特别 )()(lim 00 P f A P f D P P P ≠=∈→时，称0P 是f 的可去间断点。
第十六章 多元函数的极限与连续 ( 1 0 时 ) §1 平面点集与多元函数 ( 3 时 ) 一. 平面点集: 平面点集的表示: ),(|),{(y x y x E =满足的条件}. 1. 常见平面点集: ⑴ 全平面和半平面: }0|),{(≥x y x , }0|),{(>x y x , }|),{(a x y x >, }|),{(b ax y y x +≥等. ⑵ 矩形域: ],[],[d c b a ?, 1|||| ),{(≤+y x y x }. ⑶ 圆域: 开圆, 闭圆, 圆环. 圆的个部分. 极坐标表示, 特别是 }cos 2|),{(θθa r r ≤和}sin 2|),{(θθa r r ≤. ⑷ 角域: }|),{(βθαθ≤≤r . ⑸ 简单域:-X 型域和-Y 型域. 2. 邻域: 圆邻域和方邻域，圆邻域内有方邻域，方邻域内有圆邻域. 空心邻域和实心邻域, 空心方邻域与集 }||0 , ||0|),{(00δδ<-<<- 目录 1引言 (1) 2多元函数的连续、偏导数及可微........................... ... (1) 2.1多元函数的连续性 (1) 2.2 多元函数的偏导数 (3) 2.3多元函数的可微性 (4) 2.4多元函数连续性、偏导数存在性、及可微间的关系 (7) 2.4.1二元函数连续性与偏导存在性间的关系 (7) 2.4.2二元函数的可微性与偏导存在性间的关系 (8) 2.4.3二元函数的连续性与可微性间的关系 (10) 3小结.................................... .. (11) 参考文献 (12) 致谢辞 (13) 1 引言 对于一元函数而言，函数()y f x =在0x 极限存在、连续、可微，这三个概念的关系是很清楚的，即可微一定连续，但连续不一定可微，连续一定有极限，但有极限不一定连续.简单表示为：可微?连续?极限存在(且不可逆) 对于二元函数而言，它既不同于一元函数有可导与可微的等价关系，也没有一元函数的“可导必连续”的关系.但对于二元函数的可微性，可以证明，若二元函数(,)z f x y =在点0p (0x ,0y )可微，则函数(,)f x y 在点0p （0x ，0y ） 连续，偏导存在；若二元函数(,)z f x y =的两个偏导数'x f （x,y ）与'y f (x,y)在点0p （0x ，0y ）连续，则函数(,)f x y 在0p （0x ，0y ）可微.因此对于函数的连续、偏导存在、可微、偏导连续，有下列蕴涵关系：偏导连续?可微?(连续，偏导存在);它们反方向结论不成立. 多元函数是一元函数的推广，因此它保留着一元函数的许多性质，但也有某些差异，而且情况也更复杂一些.下面我们分别从多元函数的可微性、偏导存在性、连续性，进而到它们之间的关系进行具体的探讨. 2多元函数的连续、偏导数及可微性 2.1 多元函数的连续性 一个一元函数若在某点存在左导数和右导数，则这个一元函数必在这点连续.但对于二元函数(,)f x y 来说，即使它在某点000(,)p x y 既存在关于x 的偏导数00(,)x f x y ，又存在关于y 的偏导数00(,)y f x y ，(,)f x y 也未必在000(,)p x y 连续.甚至，即使在000(,)p x y 的某邻域0()U p 存在偏导数(,)x f x y （或(,)y f x y ），而且(,)x f x y （或(,)y f x y ）在点000(,)p x y 连续，也不能保证(,)f x y 在000(,)p x y 连续.如函数浅谈多元函数的连续
相关主题
文本预览