- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
3、 若 f ( y ) x 2 y 2 ( y 0),则 f ( x) ________.
x
y
4、
若
f
(x
y,
y )
x2
y2 ,则
f
( x,
y)
_________.
x
函数 z
4x ln(1 x 2
y2 y2
的定义域是__________. )
6、函数z x y 的定义域是______________.
引例: • 圆柱体的体积 • 定量理想气体的压强
• 三角形面积的海伦公式
r h
ba c
机动 目录 上页 下页 返回 结束
定义1. 设非空点集
映射
在 D 上的 n 元函数 , 记作
称为定义
点集 D 称为函数的定义域 ; 数集 u u f ( P ) ,P D
称为函数的值域 . 特别地 , 当 n = 2 时, 有二元函数
例如,
显然
lim lim f ( x, y) 0,
x0 y0
但由例3 知它在(0,0)点二重极限不存在 .
例3 目录 上页 下页 返回 结束
四、 多元函数的连续性
定义3 . 设 n 元函数 f (P) 定义在 D 上, 聚点P0 D,
如果存在
lim
P P0
f (P)
f (P0 )
则称 n 元函数 f (P)在点P0 连续, 否则称为不连续, 此时
机动 目录 上页 下页 返回 结束
3. n 维空间
n 元有序数组 记作 Rn,即
Rn R R R
的全体称为 n 维空间,
n 维空间中的每一个元素
称为空间中的
一个点,
称为该点的第 k 个坐标 .
当所有坐标
称该元素为 R n中的零元,记作
O.
机动 目录 上页 下页 返回 结束
Rn中的点x ( x1, x2,, xn ) 与点 y ( y1, y2,, yn )
lim
x0
f (x, y)
lim
x0
kx2 x2 k2x2
k 1 k2
ykx
k 值不同极限不同 !
故 f ( x, y)在 (0,0) 点极限不存在 .
机动 目录 上页 下页 返回 结束
例4. 求
此函数定义域 不包括 x , y 轴
解:
因
x2 y2
1 4
(
x
2
y2 )2,
令
r2
x2
y2,
则
4
(1
f
(
y
2
,
y)
(
y6 y4
y2 y4
)2
1 4
.
一、 填空题:
练习 题
1、 若 f ( x, y) x 2 y 2 xy tan x ,则 f (tx, ty) =____. y
2、 若 f ( x, y) x 2 y 2 ,则 f (2,3) __________; 2 xy
f (1, y ) ________________. x
。P0
平面上的方邻域为
U(P0,δ) ( x, y)
机动 目录 上页 下页 返回 结束
2. 区域
(1) 内点、外点、边界点
E
设有点集 E 及一点 P :
• 若存在点 P 的某邻域 U(P) E ,
则称 P 为 E 的内点;
• 若存在点 P 的某邻域 U(P)∩ E = ,
则称 P 为 E 的外点 ;
第九章 多元函数微分学
一元函数微分学 推广
多元函数微分学 注意: 善于类比, 区别异同
第一、二节
多元函数的概念
一、区域 二、多元函数的概念 三、多元函数的极限 四、多元函数的连续性
机动 目录 上页 下页 返回 结束
一、 区域
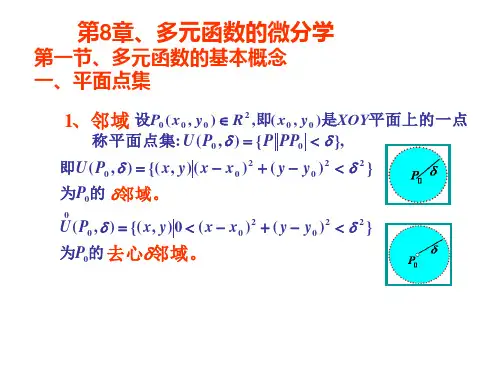
1. 邻域 点集
例如,在平面上,
U( P0 , δ) ( x, y)
在空间中,
cos r6
r
2
)
而
lim
r 0
4(1
cos r6
r
2
)
lim
r 0
2r4 r6
故
1 cos r 2~ r 4
2
机动 目录 上页 下页 返回 结束
• 二重极限 lim f ( x, y) 与累次极限 lim lim f ( x, y)
x x0
x x0 y y0
y y0
不同.
如果它们都存在, 则三者相等. 仅知其中一个存在, 推不出其它二者存在.
y y0
机动 目录 上页 下页 返回 结束
例1.
设
f (x, y) (x2
y
2
)
sin
x
2
1
y2
求证: lim f ( x, y) 0.
x0 y0
证:
( x2 y2 0)
要证
ε
ε 0, δ ε , 当0 x2 y2 δ时, 总有
x2 y2
故
lim f ( x, y) 0
的距离记作
规定为
Rn中的点x ( x1, x2,, xn )与零元 O 的距离为 x x12 x22 xn2
当n 1,2,3 时, x 通常记作 x . Rn中的变元 x 与定元 a 满足 x a 0 记作 x a.
R n中点 a 的 邻域为
机动 目录 上页 下页 返回 结束
二、多元函数的概念
( x, y) x y 0
(x, y) 1 x2 y2 4
y
y
闭区域
o
x
o 1 2x
y
o
x
y
o 1 2x
机动 目录 上页 下页 返回 结束
整个平面 是最大的开域 , 也是最大的闭域;
点集( x, y) x 1是开集,
但非区域 .
y
1o 1 x
• 对区域 D , 若存在正数 K , 使一切点 PD 与某定点 A 的距离 AP K , 则称 D 为有界域 , 否则称为无 界域 .
三元函数
机动 目录 上页 下页 返回 结束
3. 多元函数的极限
lim f (P) A
P P0
ε 0, δ 0, 当0 PP0 δ时, 有 f (P) A ε
4. 多元函数的连续性
1) 函数 f (P)在 P0 连续
lim
P P0
f (P)
f (P0 )
2) 闭域上的多元连续函数的性质:
x0
y0
机动 目录 上页 下页 返回 结束
• 若当点 P( x, y)以不同方式趋于 P0( x0, y0 ) 时, 函数 趋于不同值或有的极限不存在,则可以断定函数极限
不存在 .
例3. 讨论函数
f
( x,
y)
xy x2 y2
在点 (0, 0) 的极限.
解: 设 P(x , y) 沿直线 y = k x 趋于点 (0, 0) , 则有
(证明略)
机动 目录 上页 下页 返回 结束
例5.求 lim x y 1 1. x0 x y
y0
解: 原式
lim
1
1
x0 x y 1 1 2
y0
例6. 求函数 f ( x, y) arcsin(3 x2 y2 ) 的连续域.
x y2
解: 3 x2 y2 1
y
x y2 0
U( P0 ,) ( x, y, z )
PP0 δ 称为点 P0 的邻域.
(圆邻域)
(球邻域)
说明:若不需要强调邻域半径 ,也可写成 U ( P0 ).
点 P0 的去心邻域记为
0 PP0 δ
机动 目录 上页 下页 返回 结束
在讨论实际问题中也常使用方邻域, 因为方邻域与圆 邻域可以互相包含.
( x , y )( x0 , y0 )
思考题解答
不能.
例
f
(
x,
y)
(
x3 y2 x2 y4
)2
,
( x, y) (0,0)
取 y kx,
f
(
x,
kx)
(
x3 k2x2 x2k4 x4 )2
x0 0
但是 lim f ( x, y) 不存在.
( x , y )(0,0)
原因为若取x y2,
当 n = 3 时, 有三元函数
机动 目录 上页 下页 返回 结束
例如, 二元函数 z 1 x2 y2
定义域为圆域 ( x, y) x2 y2 1
图形为中心在原点的上半球面. 又如, z sin( x y), ( x, y) R2 说明: 二元函数 z = f (x, y), (x, y) D
切 P D U (P0,δ), 都有
则称 A 为函数
记作
lim f (P) A (也称为 n 重极限)
P P0
当 n =2 时, 记 PP0 ( x x0 )2 ( y y0 )2 二元函数的极限可写作:
lim f ( x, y) A lim f ( x, y) A
0
x x0
7、函数z arcsin y 的定义域是_______________. x
8、函数z
y2 y2
2x 的间断点是________________. 2x
二、求下列各极限:
1、lim 2 xy 4 ;
• 若点集 E E , 则称 E 为闭集;
• 若集 D 中任意两点都可用一完全属于 D 的折线相连 ,
则称 D 是连通的 ; • 连通的开集称为开区域 ,简称区域 ; • 开区域连同它的边界一起称为闭区域.
D 。。
机动 目录 上页 下页 返回 结束