高等数学多元函数微分基本概念

高等数学多元函数微积分多元函数微积分是高等数学中的一个重要分支。

它研究在多变量空间中的单变元函数的微分和积分问题。

这对学习曲面、平面的渐变、凹凸和分界、曲面的体积、局部极值等问题具有重要意义。

一、基本概念1. 超曲面：一般讲，超曲面就是在n维空间中的一类曲面，它们由至少n+1个函数组成。

它是由n维变量组成的，因而可以容纳n维量空间中所有的事物，从而形成一个多维结构。

2. 多元函数微分：多元函数微分就是对在多元空间内变量中的一个函数进行微分的一类函数，它可以应用于求解曲面的斜率，曲面的凹凸和分界，比如计算椭圆曲线、抛物曲线等的曲率和斜率等问题。

3. 多元函数积分：多元函数积分是指在多元空间中的一个函数的积分运算，它可以用于计算曲面的体积，曲面的拉伸与缩小等问题，它也可以用于计算曲面的累积，例如计算三维抛物面、回旋曲线等曲率积分的体积等。

二、求解方法1. 黎曼微积分法：黎曼微积分法是指在进行多元函数微积分时，识别出包含所求函数的一组导函数，然后根据黎曼公式将这些导函数求和，不断缩小未知函数的范围，最终确定出未知函数的表达式的一类方法。

2. 光滑函数的变换法：光滑函数的变换法指的是在进行多变量函数积分时，先将所给函数进行光滑变换，然后根据变换法则和对称性，极限性和旋转对称性等等属性，运用变换法，不断将多变量函数转化为单变量函数，最后将单变量函数进行积分。

三、应用1. 力学中的应用：多元函数微积分在力学中有着重要的作用，通过多元函数微积分，可以研究分析物体的运动轨迹，甚至可以预测未来的物体的状态。

2. 热物理学的应用：多元函数微积分可以用来研究热物理学中各种复杂多变量的函数，如热力学量在温度和压力变化时的变化情况，揭示物质性质在热状态时的性质变化，以及热流、热量变化的关系等。

3. 数学建模的应用：多元函数微积分也可以用来进行数学建模，如多元微积分可以用来描述一个普通一般问题的结构特性，如一个多边形的周长、三角形的体积、四棱锥的表面积等。

高等数学中的多元函数与多元微分导言：高等数学是大学数学的重要组成部分，它包括微积分、线性代数、概率论等多个分支。

其中，多元函数与多元微分是微积分的重要内容之一。

本文将围绕这一主题展开，探讨多元函数的概念、性质以及多元微分的应用。

一、多元函数的概念与性质1.1 多元函数的定义在高等数学中，多元函数是指自变量有两个或两个以上的函数。

一般地，我们可以将一个多元函数表示为f(x1, x2, ..., xn)，其中x1, x2, ..., xn是自变量，f是因变量。

多元函数可以用来描述现实生活中的复杂问题，如经济学中的供求关系、物理学中的力学问题等。

1.2 多元函数的性质多元函数与一元函数相比，具有更加丰富的性质。

其中，连续性、可导性和偏导数是多元函数的重要性质之一。

连续性：多元函数在定义域内的每一个点都满足连续性要求。

也就是说，在自变量的取值变化过程中，函数值变化连续，没有突变的情况。

可导性：多元函数在某一点处可导，意味着该点处的切线存在，并且切线的斜率可以通过求偏导数得到。

可导性是多元函数的重要特征，它与函数的平滑性和变化趋势密切相关。

偏导数：多元函数的偏导数是指在其他自变量保持不变的情况下，对某一个自变量求导的结果。

偏导数可以用来描述多元函数在不同方向上的变化率，它在物理学、工程学等领域具有广泛的应用。

二、多元微分的应用2.1 多元微分的定义多元微分是指对多元函数进行微分的过程。

在一元函数的微分中，我们通过求导数来描述函数在某一点的变化率。

而在多元函数的微分中，我们需要使用偏导数来描述函数在不同自变量方向上的变化率。

2.2 多元微分的应用多元微分在实际问题中有着广泛的应用。

以下是一些常见的应用场景：最优化问题：在经济学、管理学等领域中，我们经常需要求解最优化问题，即在一定的约束条件下，找到使得目标函数取得最大或最小值的自变量取值。

多元微分可以帮助我们求解这类问题，通过求偏导数和约束条件，得到最优解的自变量取值。

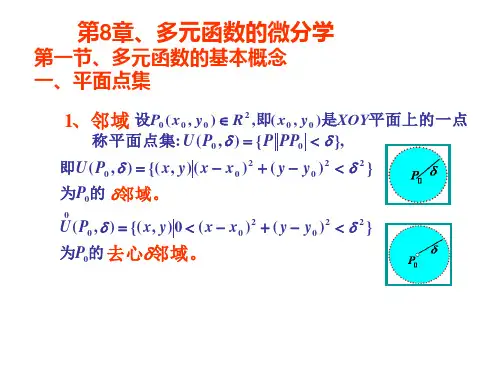
第九章 多元函数微分学§9.1 多元函数的概念、极限与连续性一、多元函数的概念1．二元函数的定义及其几何意义设D 是平面上的一个点集，如果对每个点()D y x P ∈,，按照某一对应规则f ，变量z 都有一个值与之对应，则称z 是变量x ，y 的二元函数，记以()y x f z ,=，D 称为定义域。

二元函数()y x f z ,=的图形为空间一卦曲面，它在xy 平面上的投影区域就是定义域D 。

例如 221y x z --=，1:22≤+y x D ， 此二元函数的图形为以原点为球心，半径为1的上半球面，其定义域D 就是 xy 平面上以原点为圆心，半径为1的闭圆。

2．三元函数与n 元函数()z y x f u ,,= ()Ω∈z y x ,,空间一个点集称为三元函数()n x x x f u ,,21 = 称为n 元函数它们的几何意义不再讨论，在偏导数和全微分中会用到三元函数。

条件极值中，可能会遇到超过三个自变量的多元函数。

二、二元函数的极限设函数),(y x f 在区域D 内有定义，),(000y x P 是D 的聚点，如果存在常数A ，对于任意给定的0>ε，总存在0>δ，当),(y x P 满足δ<-+-=<20200)()(0y y x x PP 时，恒有ε<-A y x f ),(成立。

则记以()A y x f y y x x =→→,lim 0或()()()A y x f y x y x =→,lim00,,。

称当()y x ,趋于()00,y x 时，()y x f ,的极限存在，极限值A ，否则称为极限不存在。

值得注意：这里()y x ,趋于()00,y x 是在平面范围内，可以按任何方式沿任意曲线趋于()00,y x ，所以二元函数的极限比一元函数的极限复杂；但考试大纲只要求知道基本概念和简单的讨论极限存在性和计算极限值，不像一元函数求极限要求掌握各种方法和技巧。

大一高数多元函数知识点总结大一的高等数学是大学学习的一门基础课程，其中多元函数是其中比较重要的一部分。

在学习多元函数时，我们需要了解一些基本的概念、性质和计算方法。

本文将对大一高数多元函数的知识点进行总结，希望对同学们的学习有所帮助。

一、多元函数的概念和性质1.1 多元函数的定义多元函数是指含有两个或两个以上自变量的函数，在平面上表示为f(x,y)，在空间中表示为f(x,y,z)。

而自变量的取值范围可以是实数集合或者某个区间，函数的值可以是实数或者向量。

1.2 驻点和极值对于多元函数，我们可以通过求偏导数的方法找到其驻点和极值。

具体来说，对于一个二元函数f(x,y)，求偏导数f’x(x,y)和f’’y(x,y)，令其等于零，可以得到驻点的坐标。

然后，通过计算二阶偏导数f’’xx(x,y)、f’’xy(x,y)和f’’yy(x,y)的值，可以判断驻点是否是极值点。

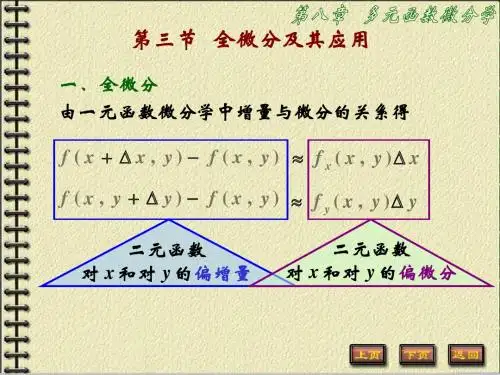
1.3 偏导数与全微分对于多元函数，我们可以通过对其中某一个自变量求偏导数的方法来求得偏导数，而偏导数可以理解为函数对于某一自变量的变化率。

而全微分则是对多元函数进行全面的微分，表示其在各个自变量方向上的变化率之和。

1.4 隐函数和参数方程在一些情况下，多元函数的表达式并不明显，而是通过一些隐含的条件进行表示。

这时要借助隐函数的概念，将多元函数用隐函数的形式表示出来。

而参数方程则是将多元函数在某个平面上表示为参数的函数形式。

二、多元函数的计算方法2.1 多元函数的线性逼近对于一个二元函数f(x,y)，我们可以通过求得其一阶偏导数和二阶偏导数，来进行函数的线性逼近。

而通过线性逼近，我们可以计算函数在某一点的近似值，以及该点处的切线和法线。

2.2 多元函数的积分多元函数的积分与一元函数的积分类似，只是需要在计算过程中考虑到多个自变量。

可以通过对其中一个自变量进行积分，将多元函数转化为一元函数的形式，然后再进行计算。

2.3 向量场的散度和旋度对于一个二维向量场和三维向量场，我们可以通过计算其散度和旋度来了解向量场的性质。