第三章-一元线性回归模型
- 格式:pdf
- 大小:942.48 KB
- 文档页数:67

第三章 一元线性回归模型一、预备知识(一)相关概念对于一个双变量总体,若由基础理论,变量和变量之间存在因果),(i i x y x y 关系,或的变异可用来解释的变异。
为检验两变量间因果关系是否存在、x y 度量自变量对因变量影响的强弱与显著性以及利用解释变量去预测因变量x y x ,引入一元回归分析这一工具。
y 将给定条件下的均值i x i yi i i x x y E 10)|(ββ+=(3.1)定义为总体回归函数(PopulationRegressionFunction,PRF )。
定义为误差项(errorterm ),记为,即,这样)|(i i i x y E y -i μ)|(i i i i x y E y -=μ,或i i i i x y E y μ+=)|(i i i x y μββ++=10(3.2)(3.2)式称为总体回归模型或者随机总体回归函数。
其中,称为解释变量x (explanatory variable )或自变量(independent variable );称为被解释y 变量(explained variable )或因变量(dependent variable );误差项解释μ了因变量的变动中不能完全被自变量所解释的部分。
误差项的构成包括以下四个部分:(1)未纳入模型变量的影响(2)数据的测量误差(3)基础理论方程具有与回归方程不同的函数形式,比如自变量与因变量之间可能是非线性关系(4)纯随机和不可预料的事件。
在总体回归模型(3.2)中参数是未知的,是不可观察的,统计计10,ββi μ量分析的目标之一就是估计模型的未知参数。
给定一组随机样本,对(3.1)式进行估计,若的估计量分别记n i y x i i ,,2,1),,( =10,),|(ββi i x y E 为,则定义3.3式为样本回归函数^1^0^,,ββi y ()i i x y ^1^0^ββ+=n i ,,2,1 =(3.3)注意,样本回归函数随着样本的不同而不同,也就是说是随机变量,^1^0,ββ它们的随机性是由于的随机性(同一个可能对应不同的)与的变异共i y i x i y x 同引起的。

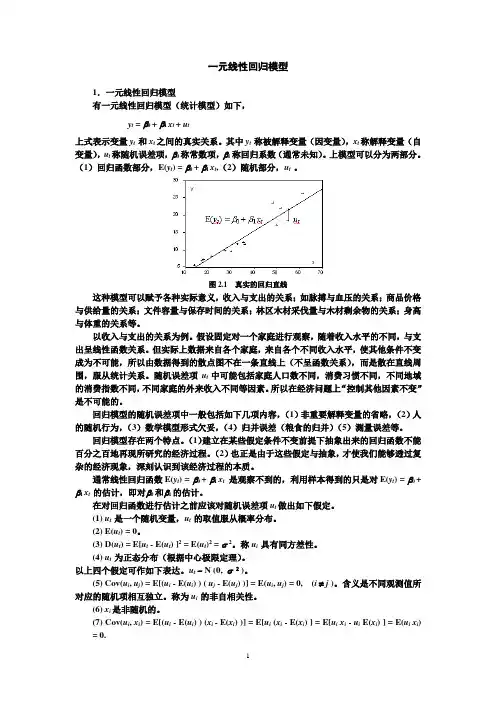
一元线性回归模型1.一元线性回归模型有一元线性回归模型(统计模型)如下,y t = β0 + β1 x t + u t上式表示变量y t 和x t之间的真实关系。
其中y t 称被解释变量(因变量),x t称解释变量(自变量),u t称随机误差项,β0称常数项,β1称回归系数(通常未知)。
上模型可以分为两部分。
(1)回归函数部分,E(y t) = β0 + β1 x t,(2)随机部分,u t。
图2.1 真实的回归直线这种模型可以赋予各种实际意义,收入与支出的关系;如脉搏与血压的关系;商品价格与供给量的关系;文件容量与保存时间的关系;林区木材采伐量与木材剩余物的关系;身高与体重的关系等。
以收入与支出的关系为例。
假设固定对一个家庭进行观察,随着收入水平的不同,与支出呈线性函数关系。
但实际上数据来自各个家庭,来自各个不同收入水平,使其他条件不变成为不可能,所以由数据得到的散点图不在一条直线上(不呈函数关系),而是散在直线周围,服从统计关系。
随机误差项u t中可能包括家庭人口数不同,消费习惯不同,不同地域的消费指数不同,不同家庭的外来收入不同等因素。
所以在经济问题上“控制其他因素不变”是不可能的。
回归模型的随机误差项中一般包括如下几项内容,(1)非重要解释变量的省略,(2)人的随机行为,(3)数学模型形式欠妥,(4)归并误差(粮食的归并)(5)测量误差等。
回归模型存在两个特点。
(1)建立在某些假定条件不变前提下抽象出来的回归函数不能百分之百地再现所研究的经济过程。
(2)也正是由于这些假定与抽象,才使我们能够透过复杂的经济现象,深刻认识到该经济过程的本质。
通常线性回归函数E(y t) = β0 + β1 x t是观察不到的,利用样本得到的只是对E(y t) = β0 + β1 x t 的估计,即对β0和β1的估计。
在对回归函数进行估计之前应该对随机误差项u t做出如下假定。
(1) u t 是一个随机变量,u t 的取值服从概率分布。



第三章一元线性回归模型第一节一元线性回归模型及其基本假设一元线性回归模型第二章回归分析的基本思想指出,由于总体实际上是未知的,必须根据样本回归模型估计总体回归模型,回归分析的目的就是尽量使得样本回归模型接近总体回归模型,那么采取什么方法估计样本回归模型才使得估计出的样本回归模型是总体回归模型的一个较好估计值呢?这里包括两个问题:一是采用什么方法估计样本回归模型;二是怎样验证估计出的样本回归模型是总体回归模型的一个较好估计值。
这些将在接下来的内容中讲到。
这一章介绍最简单的一元线性回归模型,下一章再扩展到多元线性回归模型。
一元线性回归模型及其基本假设一、一元线性回归模型的定义一元线性回归模型是最简单的计量经济学模型,在该一元模型中,仅仅只含有一个自变量,其一般形式为:yi = β0 + β1xi + μi(3.1.1)其中yi是因变量,xi是自变量,β0、β1是回归参数,μi是随机项。
由于式(3.1.1)是对总体而言的,也称为总体回归模型。
随机项μ代表未被考虑到模型中而又对被解释变量y有影响的所有因素产生的总效应。
二、一元线性回归模型的基本假设由于模型中随机项的存在使得参数β0和β1的数值不可能严格计算出来,而只能进行估计,在计量经济学中,有很多方法可以估计出这些参数值,但采用什么方法能够尽可能准确地估计出这些参数值,取决于随机项μ和自变量x的性质。
因此,对随机项μ和自变量x的统计假定以及检验这些假定是否满足的方法,在计量经济学中占有重要的地位。
估计方法中用得最多的是普通最小二乘法(Ordinary Least Squares),同样为了保证利用普通最小二乘法估计出的参数估计量具有良好的性质,也需要对模型的随机项μ和自变量x 提出若干种假设。
当模型中的随机项μ和自变量x满足这些假设时,普通最小二乘法就是适合的估计方法;当模型中的随机项μ和自变量x不满足这些假设时,普通最小二乘法就不是适合的方法,这时需要利用其他的方法来估计模型。



第三章 一元线性回归一元线性回归分析的对象是两个变量的单向因果关系,模型的核心是两变量线性函数,分析方法是回归分析。
一元线性回归是经典计量经济分析的基础。
第一节一元线性回归模型一、变量间的统计关系社会经济现象之间的相互联系和制约是社会经济的普遍规律。
在一定的条件下,一些因素推动或制约另外一些与之联系的因素发生变化。
这种状况表明在经济现象的内部和外部联系中存在着一定的因果关系,人们往往利用这种因果关系来制定有关的经济政策,以指导、控制社会经济活动的发展。
而认识和掌握客观经济规律就要探求经济现象间经济变量的变化规律。
互有联系的经济变量之间的紧密程度各不相同,一种极端的情况是一个变量能完全决 定另一个变量的变化。
比如:工业企业的原材料消耗金额用y 表示,生产量用1x 表示,单位产量消耗用2x 表示,原材料价格用3x 表示,则有:123y x x x =。
这里,y 与123,,x x x ,是一种确定的函数关系。
然而,现实世界中,还有不少情况是两个变量之间有着密切的联系,但它们并没有密切到由一个可以完全确定另一个的程度。
例如:某种高档费品的销售量与城镇居民的收入;粮食产量与施肥量之间的关系;储蓄额与居民的收入密切相关。
从图示上可以大致看出这两种关系的区别:一种是对应点完全落到一条函数曲线上;另一种是并不完全落在曲线上,而有的点在曲线上,有的点在曲线的两边。
对于后者这种不能用精确的函数关系来描述的关系正是计量经济学研究的重要内容。
二、一元线性回归模型 1.模型的建立一个例子,见教材66页:总体回归模型:01i i i Y X ββε=++ 理解:(1)误差的随机性使得Y 和X 之间呈现一种随机的因果关系;(2)Y i 的取值由两部分组成,一类是系统内影响,一类是系统外影响。
样本回归直线:01i i Y X ββ=+样本回归模型:01i i i Y X e ββ=++2.模型的假设(1) 误差项i ε的数学期望无论I 取什么值都是零。

第三章 一元经典线性回归模型的基本假设与检验问题 3.1TSS,RSS,ESS 的自由度如何计算?直观含义是什么?答:对于一元回归模型,残差平方和RSS 的自由度是(2)n -,它表示独立观察值的个数。
对于既定的自变量和估计量1ˆβ和2ˆβ,n 个残差 必须满足正规方程组。
因此,n 个残差中只有(2)n -个可以“自由取值”,其余两个随之确定。
所以RSS 的自由度是(2)n -。
TSS 的自由度是(1)n -:n 个离差之和等于0,这意味着,n 个数受到一个约束。
由于TSS=ESS+RSS ,回归平方和ESS 的自由度是1。
3.2 为什么做单边检验时,犯第一类错误的概率的评估会下调一半?答:选定显著性水平α之后,对应的临界值记为/2t α,则双边检验的拒绝区域为/2||t t α≥。
单边检验时,对参数的符号有先验估计,拒绝区域变为/2t t α≥或/2t t α≤-,故对犯第I 类错误的概率的评估下下降一半。
3.3 常常把高斯-马尔科夫定理简述为:OLS 估计量具有BULE 性质,其含义是什么? 答:含义是:(1)它是线性的(linear ):OLS 估计量是因变量的线性函数。
(2)它是无偏的(unbiased ):估计量的均值或数学期望等于真实的参数。
比如22ˆ()E ββ=。
(3)它是最优的或有效的(Best or efficient ):如果存在其它线性无偏的估计量,其方差必定大于OLS 估计量的方差。
3.4 做显著性检验时,针对的是总体回归函数(PRF )的系数还是样本回归函数(SRF )的系数?为什么?答:做显著性检验时,针对的是总体回归函数(SRF )的系数。
总体回归函数是未知的,也是研究者所关心的,所以只能利用样本回归函数来推测总体回归函数,后者是利用样本数据计算所得,是已知的,无需检验。
(习题)3.5 以下陈述正确吗?不论正确与否,请说明理由。
(1)X值越接近样本均值,斜率的OLS估计值就越精确。
第三章 一元线性回归第一部分 学习指导一、本章学习目的与要求1、掌握一元线性回归的经典假设;2、掌握一元线性回归的最小二乘法参数估计的计算公式、性质和应用;3、理解拟合优度指标:决定系数R 2的含义和作用;4、掌握解释变量X 和被解释变量Y 之间线性关系检验,回归参数0β和1β的显著性检验5、了解利用回归方程进行预测的方法。
二、本章内容提要(一)一元线性回归模型的假设条件 (1)E (i ε)=0 (i =1,2,……,n ),即随机误差项分布的均值为零。
(2)Var (i ε)=2σ (i =1,2, ……,n ),即随机误差项方差恒定,称为同方差。
(3)C o v (i ε,j ε)=0,(任意i ≠j ,i ,j =1,2, ……,n ),即随机误差项之间互不 相关。
(4)解释变量X 是非随机的,换句话说,在重复抽样下,X 的取值是确定不变的。
(5)i ε~N (0,2σ),即随机误差项服从均值为0,方差为2σ的正态分布。
前四个假定就是著名的高斯—马尔科夫假定或者称为回归分析的经典假定。
(二)一元线性回归最小二乘法估计参数的计算公式及性质 1、一元线性回归最小二乘法估计参数的计算公式为:()()()112101ˆˆˆni i xy i nxx ii x x y y S S x x y xβββ==⎧--⎪⎪==⎪⎨-⎪⎪=-⎪⎩∑∑ 2、一元线性回归最小二乘法估计参数的性质与估计量的性质 (1)残差的总和等于0,即∑=ni i1ˆε=0。
(2)残差的平方和最小,即∑=n i i12ˆε最小。
(3)被解释变量Y 的实际观测值i y 之和等于其拟合值ˆi y之和,从而i y 的均值y 与i y ˆ的均值y ˆ也相等。
(4)残差ˆi ε与ˆi y 互不相关,即1ˆˆ0ni i i y ε==∑。
(5)回归直线通过解释变量X 和被解释变量Y 的均值点(,)x y 。
3、OLS 法得到的估计量的性质(1) 线性性,即参数估计量是关于被解释变量Y 取值的线性函数。
Econometrics第三章一元线性回归模型(教材第二、三章)第三章一元线性回归模型3.1 回归的涵义3.2 随机扰动项的来源3.3 参数的最小二乘估计3.4 参数估计的性质3.5 显著性检验3.6 拟合优度3.7 预测学习要点回归模型的涵义,参数的OLS估计及其性质,显著性检验3.1 回归的涵义回归分析(regression analysis )f 用于研究一个变量(称为被解释变量或应变量)与另一个或多个变量(称为解释变量或自变量)之间的关系。
f Y 代表被解释变量,X 代表解释变量;解释变量有多个时,用X1,X 2,X 3等表示。
f 例:商品的需求量与该商品价格、消费者收入以及其他竞争性商品价格之间的关系。
总体回归函数(f 例:学生的家庭收入与数学分数有怎样的关系?3.1 回归的涵义3.1 回归的涵义总体回归函数(population regression function,PRF)f根据上面数据做散点图3.1 回归的涵义总体回归函数(f 上图中,圆圈点称为条件均值;条件均值的连线称为总体回归线。
3.1 回归的涵义样本回归函数(sample regression function, SRF )f 实际中往往无法获得整个总体的数据,怎么估计总体回归函数?即如何求参数B 1、B 2?f 通常,我们仅仅有来自总体的一个样本。
f 我们的任务就是根据样本信息估计总体回归函数。
f 怎么实现?3.1 回归的涵义样本回归函数(sample regression function, SRF )f 表2-2、2-3的数据都是从表2-1中随机抽取得到的。
3.1 回归的涵义样本回归函数(sample regression function, SRF)f通过散点得到两条“拟合”样本数据的样本回归线。
3.1 回归的涵义样本回归函数(f 可用样本回归函数(3.1 回归的涵义样本回归函数(sample regression function, SRF)f回归分析:根据样本回归函数估计总体回归函数。
3.1 回归的涵义“线性”回归的特殊含义f 对“线性”有两种解释:变量线性和参数线性。
变量线性:例如前面的总体(或样本)回归函数;下3.2 随机扰动项的来源f 总体回归函数说明在给定的家庭收入下,美国学生平均的数学分数。
f 但对于某一个学生,他的数学分数可能与该平均水平有偏差。
f 可以解释为,个人数学分数等于这一组的平均值加上或减去某个值。
用数学公式表示为:其中,表示随机扰动项,简称扰动项。
扰动项是一个随机变量,通常用概率分布来描述。
12i i iY B B X u =++i u3.2 随机扰动项的来源f 对于回归模型f 称为被解释变量(explained variable )也称应变量或因变量(dependent variable )称为解释变量(explanatory variable )也称自变量(independent variable )称为参数(parameter )称为随机扰动项(random error term )12i i iY B B X u =++i u i Y i X 12,B B3.2 随机扰动项的来源f 上式如何解释?可以认为,在给定家庭收入水平3.2 随机扰动项的来源f3.2 随机扰动项的来源f性质1:扰动项代表了未纳入模型变量的影响。
例如个人健康状况、居住区域等等。
包括了决定数学分数的所有变量,其内在随机性也不可避免,这是做任何努力都无法解释的。
等于真实值。
f性质4:“奥卡姆剃刀原则”——即描述应该尽可能简单,只要不遗漏重要的信息,此时可以把影响Y的次要因素归入随机扰动项。
3.3 参数的最小二乘估计参数估计:普通最小二乘法(OLS )f 根据样本回归函数估计总体回归函数,要回答两个问题:如何估计PRF ?如何验证估计的PRF 是真实的PRF 的一个“好”的估计值?f 这里先回答第一个问题。
f 回归分析中使用最广泛的是普通最小二乘法(method of ordinary least squares, OLS )3.3 参数的最小二乘估计参数估计:普通最小二乘法(OLS )f 最小二乘原理:由于不能直接观察PRF :所以用SRF来估计它,因而f 最好的估计方法是,选择使得残差尽可能小。
12i i iY B B X u =++12i i i Y b b X e =++12ˆ i i ii ii ie Y Y Y Y Y b b X =−=−=−−实际的估计的12b b 、i e3.3 参数的最小二乘估计参数估计:普通最小二乘法(f 普通最小二乘法就是要选择参数方和3.3 参数的最小二乘估计参数估计:普通最小二乘法(f 如何确定根据微积分,当3.3 参数的最小二乘估计参数估计:普通最小二乘法(f 以上联立方程组称为正规方程组(求解3.3 参数的最小二乘估计参数估计:普通最小二乘法(f OLS例子:数学S.A.T分数3.3 参数的最小二乘估计例子:数学S.A.T 分数f 根据公式可以得到回归结果:ˆ432.41380.0013i iY X =+3.3 参数的最小二乘估计例子:数学S.A.T 分数f 根据公式可以得到回归结果:f对估计结果的解释:斜率系数0.0013表示在其他条件保持不变的情况下,家庭年收入每增加1美元,数学S.A.T.分数平均提高0.0013分截距432.4138表示,当家庭年收入为0时,数学平均分大约为432.4138。
(这样的解释没有什么经济意义)对截距最好的解释是,它代表了回归模型中所有省略变量对Y 的平均影响。
ˆ432.41380.0013i i Y X =+3.3 参数的最小二乘估计例子:受教育年限与平均小时工资f 预期平均工资随受教育年限的增加而增加f 回归结果:ˆ0.01440.7241i iY X =−+3.3 参数的最小二乘估计例子:股票价格与利率f经济理论表明,股票价格和利率之间存在反向关系。
3.3 参数的最小二乘估计例子:股票价格与利率f 看起来两个变量之间的关系不是线性的(即不是直线),因此,假设实际关系如下:3.4 参数估计的性质古典线性回归模型(CLRM)的假定f下面我们要回答“怎样判别它是真实PRF的一个好的f只有假定了随机扰动项u的生成过程,才能判定SRF对PRF拟合得是好是坏。
OLS估计量的推导与随机扰动项的生成过程无关;但根据SRF进行假设检验时,就必须对随机扰动项的生成做f下面仍然沿用一元线性回归模型来讨论。
3.4 参数估计的性质古典线性回归模型(CLRM )的假定f 假定1. 回归模型是参数线性的,但不一定是变量线性的。
回归模型形式如下(可扩展到多个解释变量):f 假定2. 解释变量与随机扰动项不相关。
如果X是非随机的,该假定自动满足;即使X 是随机的,如果样本容量足够大,也不会对分析产生严重影响。
12i i iY B B X u =++X u古典线性回归模型(f假定()3.4 参数估计的性质古典线性回归模型(CLRM )的假定f 假定4. 同方差(homoscedastic ),即i u ()2var i u σ=3.4 参数估计的性质古典线性回归模型(CLRM )的假定f 假定5. 无自相关(no autocorrelation ),即两个扰动项之间不相关:()cov ,0,i j u u i j=≠3.4 参数估计的性质古典线性回归模型(CLRM)的假定差或设定误差。
f为什么需要以上6个假定?这些假定现实吗?如果不满足这些假定,情况又会怎样?如何得知是否满足所f这些重要的问题暂时没有答案,事实上,教材“第二部分”都是围绕“如果假定不满足时会怎样”而展开的。
3.4 参数估计的性质OLS f 有了上述假定后可以计算出估计量的方差和标准差。
OLS3.4 参数估计的性质OLS f 根据下式估计OLS3.4 参数估计的性质估计结果的报告f 估计的数学SAT函数如下(括号内数字为标准差):OLS 估计量的性质f 可以概括为高斯-马尔柯夫定理(Gauss-Markov theorem ):如果满足古典线性回归模型的基本假定,则在所有线性估计两种,OLS 估计量具有最小方差性,即OLS 估计是最优线性无偏估计量(BLUE )。
f 具体见教材PP46。
()()ˆ432.41380.001316.9061 0.000245i iY X se =+=3.5 显著性检验OLS 估计量的抽样分布或概率分布f 知道如何计算OLS 估计量及其标准差仍然不够,必须求出其抽样分布才能进行假设检验。
f 为了推导抽样分布,再增加一条假定。
f 假定7.在总体回归函数中,扰动项服从均值为0,方差为的正态分布。
即f 为什么可以作这样一个假定?12i i i Y B B Xu =++i u 2σ()20,i u N σ3.5 显著性检验OLS 估计量的抽样分布或概率分布ff 可以证明,是的线性函数,根据“正态变量的线性函数仍服从正态分布”,得知服从正态分布。
f 中心极限定理:随着样本量的增加,独立同分布随机变量构造的统计量近似服从正态分布。
i u ()2120,i u N b b σ⇒ 、的概率分布?12b b 、12b b 、3.5 显著性检验OLS 估计量的抽样分布或概率分布f()()12221122,,,b b b N B bN B σσ3.5 显著性检验假设检验f 假定:家庭年收入对学生的数学成绩没有影响3.5 显著性检验假设检验f3.5 显著性检验假设检验:置信区间法f在数学H3.5 显著性检验假设检验:置信区间法f 整理3.5 显著性检验假设检验:置信区间法f图形(教材有误)0.00074 0.001873.5 显著性检验假设检验:置信区间法f 按照上述过程,同样可得截距95%的置信区间:f 如果,则显然拒绝零假设,因为上述95%的置信区间不包括0。
f 如果,则不能拒绝该假设,因为95%的置信区间包括了这个值。
1B 1393.4283471.3993B ≤≤0111:0,:0H B H B =≠0111:400,:400H B H B =≠3.5 显著性检验假设检验:显著性检验法f 核心思想是根据从样本数据求得的检验统计量的值决定接受或拒绝零假设。
3.5 显著性检验假设检验:显著性检验法f 在具体进行t 检验时f (1)对于一元线性回归模型(双变量模型),自由度为(n-2)。
f (2)常用的显著水平有1%、5%或10%。
为了避免选择显著水平的随意性,通常求出p 值(精确的显著水平),如果计算的p 值充分小,则拒绝零假设。
f (3)可用单边或双边检验。
α。